Allmänt
Lecturer: Harri Ehtamo
Assistant: Anton von Schantz
NOTE!
The first lecture is on Wed 16.1.2019 14:15-16:00 in U5,
and the first exercise session on Tue 22.1.2019 14:15-16:00 in U7.
Exam times:
Tue 9.4.2019 13-16
Fri 31.5.2019 13-16
Why this course?
This course examines dynamic (aka multistage) optimization models. They capture many relevant real-life problems: scheduling, route planning, solving optimal strategies for games, inventory control, investment problems, machine repair, text processing, dna sequence matching, stopping problems, airplane/rocket flight path optimization, minimum time/effort problems, optimal fishery management, saving/consumption optimization, optimal feedback controllers for plants and regulator problems and so on.
The models that are examined are
- Optimal control problem. Find control u(t) that makes the system
![\dot{\textbf{x}}(t) = \textbf{a}\,[\,\textbf{x}(t),\textbf{u}(t),t\,],](https://upload.wikimedia.org/math/5/9/a/59a7f1fdee9439353c912811390f5f03.png)
trace the optimal trajectory x*(t) that minimizes the cost ![J=\Phi\,[\,\textbf{x}(t_0),t_0,\textbf{x}(t_f),t_f\,] + \int_{t_0}^{t_f} \mathcal{L}\,[\,\textbf{x}(t),\textbf{u}(t),t\,] \,\operatorname{d}t](https://upload.wikimedia.org/math/3/d/0/3d0f090dd8333dacf8d6b6d43d6cec9f.png)
.
Function a describes how the system behaves at state x(t) at time t under control u(t). The cost function J consists of start and end point costs and running cost that is given by function L that may depend on the state x(t) and control u(t). - Calculus of variations. Find continuous/differentiable curve y(x) that is extremum for
![J[y] = \int_{x_1}^{x_2} L[x,y(x),y'(x)]\, dx \, .](https://upload.wikimedia.org/math/f/0/e/f0e0b0b814b75b062db8c4c6592ca3ad.png)
- Dynamic Programming (DP) problem. Find optimal controls u_k (optimal policy) that minimizes the expected cost
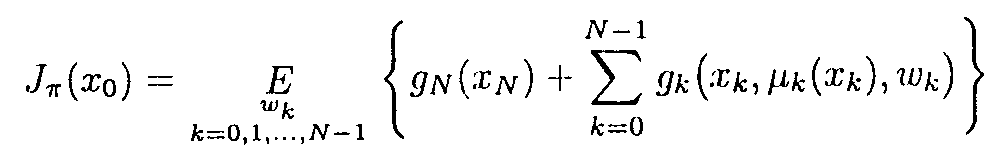
of the discrete stochastic system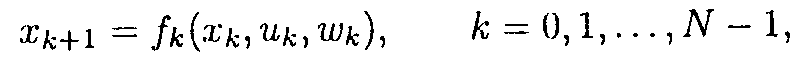
f_k describes how the system evolves to the next state x_k+1 when the state is x_k, control u_k is chosen and there is stochastic disturbance is w_k. The cost function is given by g_k. This is discrete version of the optimal control problem.
Practical matters
Teaching: Lectures (24h) and exercise sessions (24h)
Assessment methods: Exam (100%), extra points from homework and exercises
Grading scale: 0-5
Study material: Lecture slides and exercises. Additional reading:
- D. E. Kirk: Optimal Control Theory. Prentice Hall, 1970 (2004). (<- the main book)
- D. P. Bertsekas: Dynamic Programming and Optimal Control, vol 1(and 2). Athena Scientific, 1995
- M. L. Kamien and N. L. Schwartz: Dynamic Optimization - The calculus of variations and optimal control in economics and management, 2nd edition. North Holland, 1991.
Language of instruction: English
Prerequisites: 1st and 2nd years math, recommended MS-C2105 Optimoinnin perusteet (or equivalent)