MS-A0004 - Matriisilaskenta (CHEM,ELEC2, ENG2), Luento-opetus, 13.9.2021-28.10.2021
This course space end date is set to 28.10.2021 Search Courses: MS-A0004
Topic outline
-
-
Mitkä?
Täältä löydät viikoittaisen opintosuunnitelman jokaiselle kurssin opetusviikolle. Pääidea on seurata suunnitelmaa viikottain, ja jokaiseen viikkoon on laitettu ajoitukset milloin suositellaan käydä läpi materiaalit ja tehtävät. Yleisesti suosittelen seuraavaa opiskelujärjestystä jokaiselle viikolle (maanantai - perjantai), mutta katso alempana jokaiselle viikolle oma viikkosuunnitelma ja aiheet.- Tee edellisen viikon verkkotehtävät tiistaihin 17:00 mennessä. Jokaiselle viikolle on kokoelma verkkotehtäviä, jotka suositellaan tehtävän omana aikana viikon loppuun mennessä. Verkkotehtävistä saa per tehtävä 0-2 pistettä. Huomaa, että viikon 1 tehtävät palautetaan viimeistään tiistaina viikolla 2, jne.
- Palauta edellisen viikon loppuviikon tehtävät tiistaihin 17:00 mennessä. Jokaisessa laskuharjoituksessa on kaksi tehtävää jotka palautetaan alkuviikosta tänne arvioitavaksi. Kumpikin tehtävä arvioidaan asteikolla 0-4. Huomaa, että viikon 1 tehtävät palautetaan viimeistään tiistaina viikolla 2, jne.
- Osallistu alkuviikon laskuharjoitukseen (ma, ti tai ke). Joka viikon alussa on laskuharjoitus, jossa käydään kaksi alkuviikon tehtävää. Laskuharjoituksessa laskettavista tehtävistä saa 0-2 pistettä per tehtävä. Huomaa, että viikolla 1 ei ole alkuviikon laskuharjoitusta lainkaan.
- Opiskele viikon materiaali torstaihin mennessä. Käytännössä tämä tarkoittaa sitä, että käyt läpi viikon luentovideot aiheista ja luet vastaavat luentoprujun sivut (pruju saatavilla osiossa Materiaalit)
- Osallistu torstain live Zoom kertaussessioon klo 10-11. Tässä kertaus-sessiossa kertaamme läpi tämän viikon videoiden aiheita, ja oletuksena on, että olet tutustunut aiheisiin ennen tätä sessiota. Täällä voit myös kysyä vaikeista asioista. Käymme myös tässä livesessiossa lyhyesti ensi viikon aiheista. Tämä kertaus-sessio nauhoitetaan, ja laitan sen tänne, jos ei pääse paikanpäälle. Kuitenkin suosittelen tulemaan koska täällä voi suoraan kysyä kysymyksiä livenä minulta. Zoomin tiedot: Zoom meeting ID 68625046500, linkki: https://aalto.zoom.us/j/68625046500, passcode: matriisi
- Palauta alkuviikon tehtävät perjantaihin 17:00 mennessä. Jokaisessa laskuharjoituksessa on kaksi tehtävää jotka palautetaan alkuviikosta tänne arvioitavaksi. Kumpikin tehtävä arvioidaan asteikolla 0-4.
- Osallistu loppuviikon laskuharjoitukseen (to tai pe). Joka viikon lopussa on laskuharjoitus, jossa käydään kaksi tehtävää laskuharjoitus-tehtävistä. Laskuharjoituksessa laskettavista tehtävistä saa 0-2 pistettä per tehtävä.
- Itsearviointi. Yritä joka viikon lopussa katsoa mitä arvioita ja palautetta sait viikkotehtävistä ja arvioi omaa suoritustasi. Minkä arvosanan antaisit itsellesi? Mitä olisi parannettavaa ratkaisuissasi? Mikä oli vaikeaa ja mikä helppoa? Oliko "ahaa"-elämyksiä? Itsearviointeja ei arvostella mutta niitä voi vapaaehtoisesti palauttaa P tehtävien yhteydessä, jotta assistentit näkevät miten on mennyt kurssin kanssa ja voivat mahdollisesti antaa palautetta.
Huomaa siis, että vaikka Sisuun on varattu ajat luennoille, niistä järjestetään livenä vain ensimmäinen tunti torstaisin 10:15-11:00 Zoomissa (kohta 5. yllä) ja tämä on enemmän Question and Answers henkinen kertaustunti viikon aiheista. Luennot on jaettu pieniin videoihin, jotka ovat esinauhoitettu eri aiheista YouTubeen (katso esim. Viikko 1 alla), ja tarkoituksena on, että niitä voi katsoa sitten omana aikana ennen torstain tuntia.
Muista aina että voit osallistua laskutupaan ( https://laskutupa.zulipchat.com ) tai laittaa viestiä kurssin MS-A0004 Zulipiin ( https://ms-a0004.zulip.cs.aalto.fi/ )
- Katso vielä nauhoittamani johdantovideo ennen kuin siirryt Viikon 1 materiaaleihin (Linkki Videoon Aalto Panopto). Kopiot johdantovideon PDF kalvoista on tässä kansiossa alhaalla.
- Huomaa, että sanoin videolla että kurssi on suunnattu EST-, ENY-, RYM-hakukohteisssa, Kemian tekniikan kandidaattiohjelmissa tai Avoimessa yliopistossa opiskeleville. Kuitenkin kurssille saa kaikki tulla jos haluaa! Tuo kommentti oli vain siltä varalta jos opiskelija on vahingossa ottanut väärän kurssin.
Onnea kurssin kanssa!
-
Viikko 1. Vektorit ja kompleksiluvut
(13.9.2021 - 19.9.2021)Viikon oppimistavoitteet:
- Osaat määritellä vektorit, pistetulon, ristitulon, napakoordinaatit ja kompleksiluvut
- Osaat visualisoida vektoreita ja kompleksilukuja geometrisesti
- Osaat tehdä aritmeettisia ja geometrisia operaatioita vektoreilla ja kompleksiluvuilla
Tavoitteena näillä käsitteillä on saada hyvä tausta vektoreihin, jotka ovat tärkeässä roolissa matriisien kanssa, jotka kuvaavat operaatioita vektoreilla.
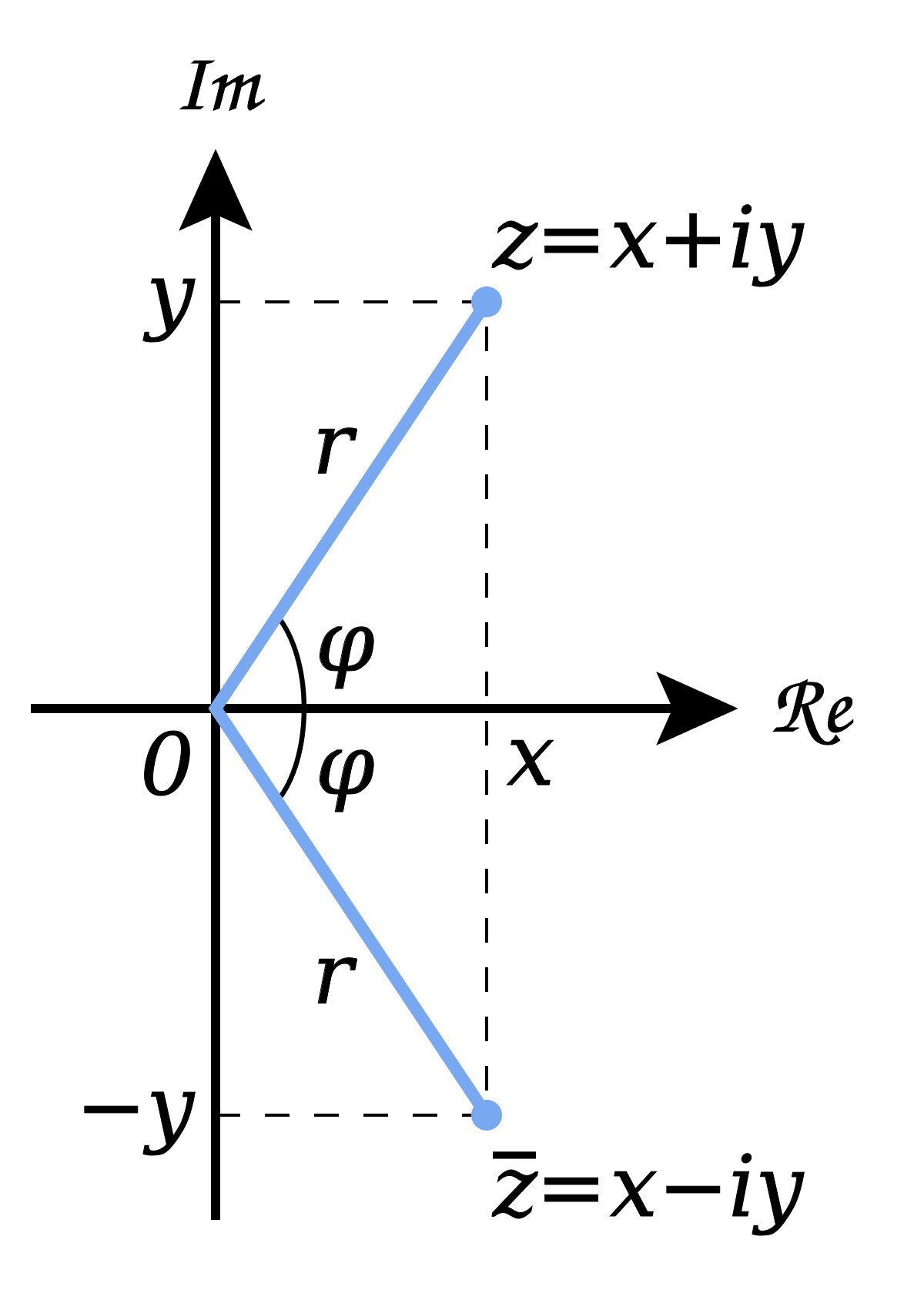 Kuva: Lisäämällä imaginaariyksikkö i reaalilukuihin saamme kompleksiluvut. Näitä voi visualisoida geometrisesti vektoreina tasossa.Aktiviteetit ennen torstain kertaussessiota:1. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):
Kuva: Lisäämällä imaginaariyksikkö i reaalilukuihin saamme kompleksiluvut. Näitä voi visualisoida geometrisesti vektoreina tasossa.Aktiviteetit ennen torstain kertaussessiota:1. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):- Video: Vektorit (linkki)
- Video: Vektorien koordinaatisto (linkki)
- Video: Skalaaritulo ja ortogonaalisuus (linkki)
- Video: Vektoritulo (linkki)
- Video: Napakoordinaatit (linkki)
- Video: Kompleksiluvut ja napakoordinaatit (linkki)
- Video: Kompleksiluvut ja sovellukset (linkki)
- Lue oppimateriaali (1-2 tuntia):
- Lue osio 1 prujuista (prujun PDF on Materiaalit osiosta)
- Käsinkirjoitetut nootit videoilta (PDF alhaalla)
Torstain kertaussessio:
2. Osallistu kertaussessioon (1 tunti) Zoomissa:- Zoomissa Torstaina, kello 10:15-11:00, Zoom meeting ID 68625046500, linkki: https://aalto.zoom.us/j/68625046500, passcode: matriisi
- Kertaussession nauhoitus (linkki)
- Käsinkirjoitetut nootit kertaussessiosta (PDF alhaalla)
Aktiviteetit torstain kertaussession jälkeen:
3. Osallistu loppuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti
4. Tee ja palauta loppuviikon laskaritehtävät ensi viikon tiistaihin klo 17 mennessä.
5. Tee verkkotehtävät ensi viikon tiistaihin klo 17 mennessä.
6. Itsearviointi. Arvioi oma opiskelusi. Minkä arvosanan antaisit itsellesi? Mitä olisi parannettavaa ratkaisuissasi? Mikä oli vaikeaa ja mikä helppoa? Oliko "ahaa"-elämyksiä?
-
Viikko 2. Matriisit ja lineaarisen yhtälöryhmän ratkaiseminen
(20.9.2021 - 26.9.2021)Viikon oppimistavoitteet:
- Osaat määritellä matriisit ja matriisiyhtälön
- Osaat esittää lineaarisen yhtälöryhmän matriisiyhtälönä
- Osaat ratkaista matriisiyhtälön Gaussin algoritmilla
- Osaat ratkaistaa alimäärätyn yhtälöryhmän Gaussin algoritmilla
Tämän viikon tavoitteena on määritellä matriisin käsite ja näyttää miten niillä voi ratkaista lineaarisia yhtälöryhmiä. Matriisit itsessään ovat erittäin hyödyllinen käsite sekä matematiikassa että sovelluksissa kuten suuren datan analysoinnissa ja koneoppimisessa, jossa matriisi voidaan mallintaa kuvaamaan esimerkiksi tietokantaa. Tällöin tämän viikon metodit kuten Gaussin algoritmi auttaa datan ymmärtämisessä. Palaamme tähän aiheeseen myöhemmillä viikoilla.
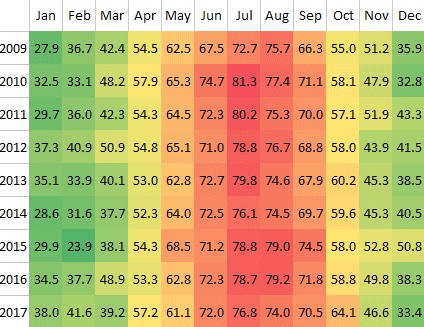 Kuva: Esimerkki yksinkertaisesta matriisista luotuna datan avulla. Tämä on niin sanottu "Heat Map" joka kuvaa New Yorkin Central Parkin keskilämpötiloja eri kuukausina Fahrenheit asteikolla. Kuva (c) excel-easy.comAktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):
Kuva: Esimerkki yksinkertaisesta matriisista luotuna datan avulla. Tämä on niin sanottu "Heat Map" joka kuvaa New Yorkin Central Parkin keskilämpötiloja eri kuukausina Fahrenheit asteikolla. Kuva (c) excel-easy.comAktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):- Video: Yhtälöryhmä matriisimuodossa (linkki)
- Video: Kolme eri mahdollisuutta ratkaisujen lukumäärälle (linkki)
- Video: Gaussin eliminaatio (linkki)
- Video: Esimerkki Gaussin eliminaatiosta ja virtapiirilasku (linkki)
- Video: Esimerkki kun on äärettömän monta ratkaisua (linkki)
- Video: Helpompi esimerkki kun on äärettömän monta ratkaisua (linkki)
- Video: Lause ratkaisujen lukumäärästä (linkki)
- Video: Sovellukset talousdynamiikkaan ja kemiaan (linkki)
- Lue oppimateriaali (1-2 tuntia):
- Lue osio 2 prujuista (prujun PDF on Materiaalit osiosta)
- Käsinkirjoitetut nootit videoilta (PDF alhaalla)
Torstain kertaussessio:
3. Osallistu kertaussessioon (1 tunti) Zoomissa:- Zoomissa Torstaina, kello 10:15-11:00, Zoom meeting ID 68625046500, linkki: https://aalto.zoom.us/j/68625046500, passcode: matriisi
- Kertaussession nauhoitus (linkki)
- Käsinkirjoitetut nootit kertaussessiosta (PDF alhaalla)
Aktiviteetit torstain kertaussession jälkeen:
4. Osallistu loppuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti
5. Tee ja palauta alkuviikon laskuharjoituksesi osiossa "Tehtävät" perjantaihin klo 17 mennessä.
6. Tee verkkotehtävät ensi viikon tiistaihin klo 17 mennessä.
7. Tee ja palauta loppuviikon laskaritehtävät ensi viikon tiistaihin klo 17 mennessä.
8. Itsearviointi. Arvioi oma opiskelusi. Minkä arvosanan antaisit itsellesi? Mitä olisi parannettavaa ratkaisuissasi? Mikä oli vaikeaa ja mikä helppoa? Oliko "ahaa"-elämyksiä?
-
Viikko 3. Matriisit ja lineaarikuvaukset
(27.9.2021 - 3.10.2021)Viikon oppimistavoitteet:
- Osaat visualisoida matriisia geometrisesti lineaarikuvauksena, joka muuttaa vektoreiden suuntaa ja pituutta
- Osaat tehdä laskutoimituksia matriiseilla
- Osaat määritellä käänteismatriisin ja löytää käänteismatriisin
Tällä viikolla yhdistämme ensimmäisen viikon käsitteet vektoreista ja toisen viikon käsitteen matriiseista yhteen ja tuomme mukaan geometrisen lähestymistavan matriiseihin. Ajatuksena on hallita matriisien käsite geometrisemmin, jolloin matriiseille voi määritellä erilaisia geometrisia ominaisuuksia kuten vektorien venyttäminen, kiertäminen ja peilaaminen.
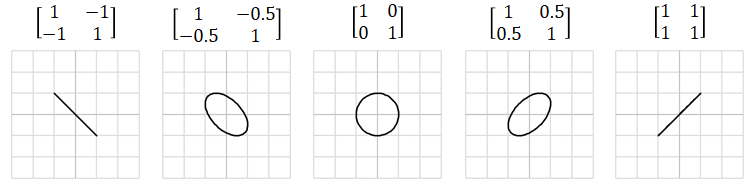 Kuva: Eri tapoja miten matriisit esitettynä lineaarikuvauksina voi venyttää yksikköympyrää tasossa. Keskellä on diagonaalimatriisi identtinen matriisi, joka ei tee mitään ja muut matriisit muokkaavat ympyrän ellipsiksi tai jopa puristavat pelkäksi viivaksi! (c) cookierobotics.com.Aktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):
Kuva: Eri tapoja miten matriisit esitettynä lineaarikuvauksina voi venyttää yksikköympyrää tasossa. Keskellä on diagonaalimatriisi identtinen matriisi, joka ei tee mitään ja muut matriisit muokkaavat ympyrän ellipsiksi tai jopa puristavat pelkäksi viivaksi! (c) cookierobotics.com.Aktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):- Video: Matriisien tulkinta lineaarikuvauksina (linkki)
- Video: Lineaarikuvausten esitys standardikannassa (linkki)
- Video: Matriisien geometrinen intuitio (linkki)
- Video: Matriisien laskutoimitukset ja tulomatriisi (linkki)
- Video: Esimerkkejä tulon laskemisesta (linkki)
- Video: Lineaarikuvauksen esitys yksinkertaisten matriisien tulona (linkki)
- Video: Transpoosi, käänteismatriisi ja nimityksiä eri matriiseille (linkki)
- Video: Käänteismatriisin laskeminen Gaussin eliminaatiolla (linkki)
- Lue oppimateriaali (1-2 tuntia):
- Lue osiot 3.1, 3.2, 3.3 ja 3.4 prujusta (Pruju Materiaalit osiossa)
- Käsinkirjoitetut nootit videoilta (PDF alhaalla)
Torstain kertaussessio:
3. Osallistu kertaussessioon (1 tunti) Zoomissa:- Zoomissa Torstaina, kello 10:15-11:00, Zoom meeting ID 68625046500, linkki: https://aalto.zoom.us/j/68625046500, passcode: matriisi
- Kertaussession nauhoitus (linkki)
- Käsinkirjoitetut nootit kertaussessiosta (PDF alhaalla)
Aktiviteetit torstain kertaussession jälkeen:
4. Osallistu loppuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti
5. Tee ja palauta alkuviikon laskuharjoituksesi osiossa "Tehtävät" perjantaihin klo 17 mennessä.
6. Tee verkkotehtävät ensi viikon tiistaihin klo 17 mennessä.
7. Tee ja palauta loppuviikon laskaritehtävät ensi viikon tiistaihin klo 17 mennessä.
8. Itsearviointi. Arvioi oma opiskelusi. Minkä arvosanan antaisit itsellesi? Mitä olisi parannettavaa ratkaisuissasi? Mikä oli vaikeaa ja mikä helppoa? Oliko "ahaa"-elämyksiä?
-
Viikko 4. Determinantti ja ominaisarvoteoria
(4.10.2021 - 10.10.2021)Viikon oppimistavoitteet:
- Osaat määritellä matriisin determinantin ja laskea sen
- Osaat määritellä ja laskea matriisin ominaisarvot ja ominaisvektorit
Ominaisarvoteoria on yksi matriisien tärkeimmistä työkaluista etenkin sovelluksissa. Esimerkiksi Googlen alkuperäinen PageRank algoritmi rakennettiin ominaisarvoteorian avulla hyvin nopeasti luokittelemaan nettisivujen merkittävyyttä. Samoin modernissa data-analyysissä ominaisavaruuksilla voidaan tehdä niin sanottu pääkomponenttianalyysi (PCA, Principal Component Analysis) sotkuiseen ja meluisaan dataan, jotta siitä voisi löytää jotain rakennetta. Tämän viikon työkalut antavat näille sovelluksille hyvän johdannon ja pohjan.

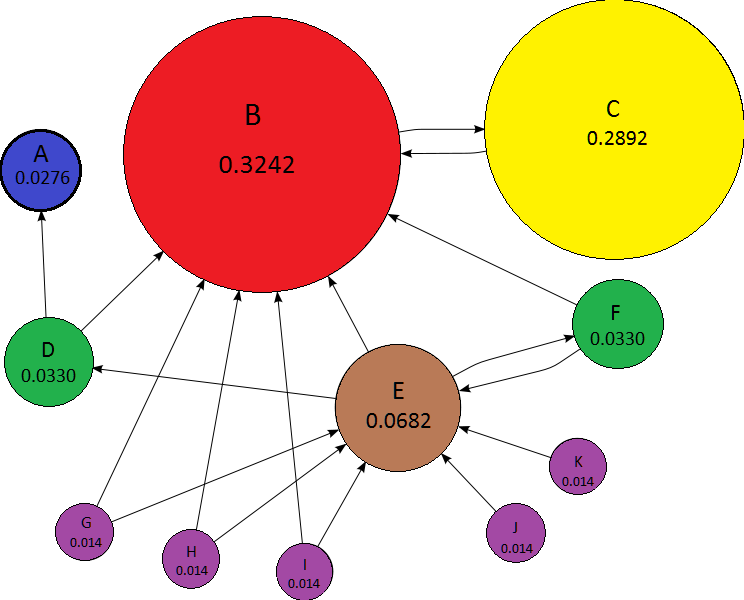 Kuva: Vasemmalla: Ominaisarvoteoriassa etsimme vektoreita x = (x,y), joiden skalaariskaalaus λ verran λx on sama kuin Ax. Tällöin näiden vektorien virittämässä hypertasossa (ominaisavaruus) matriisi A käyttäytyy kuin diagonaalimatriisi joka venyttää jokaista koordinaattia λ verran. Oikealla: Pieni internet verkko ja linkkejä sivujen välillä. Sivun palloa vastaava koko kertoo kuinka merkittävä/vaikuttava sivu on. Googlen PageRank on algoritmi, joka pyrkii luokittelemaan internet sivut niiden merkittävyyden kanssa löytämällä linkkien avulla muodostetun matriisin ominaisvektorin sopivalla ominaisarvolla. Kuva Wikimedia Commons.Aktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):
Kuva: Vasemmalla: Ominaisarvoteoriassa etsimme vektoreita x = (x,y), joiden skalaariskaalaus λ verran λx on sama kuin Ax. Tällöin näiden vektorien virittämässä hypertasossa (ominaisavaruus) matriisi A käyttäytyy kuin diagonaalimatriisi joka venyttää jokaista koordinaattia λ verran. Oikealla: Pieni internet verkko ja linkkejä sivujen välillä. Sivun palloa vastaava koko kertoo kuinka merkittävä/vaikuttava sivu on. Googlen PageRank on algoritmi, joka pyrkii luokittelemaan internet sivut niiden merkittävyyden kanssa löytämällä linkkien avulla muodostetun matriisin ominaisvektorin sopivalla ominaisarvolla. Kuva Wikimedia Commons.Aktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):- Video: Determinantti ja sen laskeminen (linkki)
- Video: Internet sivujen merkittävyys, Google PageRank ja ominaisvektorit (linkki, Huom. Pieni typo videossa kun kirjoitin matriisin P, yksi rivi unohtui. Prujussa, joka kannattaa pitää vieressä videota katsoessa, on oikea 6 x 6 matriisin määritelmä)
- Video: Ominaisarvot, -vektorit ja -avaruudet (linkki, Huom. Videon lopussa ominaisavaruudessa pitäisi sallia myös nollavektori mukaan)
- Video: Ominaisavaruuksien laskeminen (linkki)
- Video: Esimerkki 3 x 3 matriisin ominaissuorien laskemisesta (linkki)
- Lue oppimateriaali (1-2 tuntia):
- Lue osiot, 3.3, 4.1 ja 4.2 prujusta (Pruju Materiaalit osiossa)
- Käsinkirjoitetut nootit videoilta (PDF alhaalla)
Torstain kertaussessio:
3. Osallistu kertaussessioon (1 tunti) Zoomissa:- Zoomissa Torstaina, kello 10:15-11:00, Zoom meeting ID 68625046500, linkki: https://aalto.zoom.us/j/68625046500, passcode: matriisi
- Kertaussession nauhoitus (linkki)
- Käsinkirjoitetut nootit kertaussessiosta (PDF alhaalla)
Aktiviteetit torstain kertaussession jälkeen:
4. Osallistu loppuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti
5. Tee ja palauta alkuviikon laskuharjoituksesi osiossa "Tehtävät" perjantaihin klo 17 mennessä.
6. Tee verkkotehtävät ensi viikon tiistaihin klo 17 mennessä.
7. Tee ja palauta loppuviikon laskaritehtävät ensi viikon tiistaihin klo 17 mennessä.
8. Itsearviointi. Arvioi oma opiskelusi. Minkä arvosanan antaisit itsellesi? Mitä olisi parannettavaa ratkaisuissasi? Mikä oli vaikeaa ja mikä helppoa? Oliko "ahaa"-elämyksiä?
-
Viikko 5. Ominaisarvoteorian sovellukset
(11.10.2021 - 17.10.2021)Viikon oppimistavoitteet:
- Osaat soveltaa ominaisarvoteoriaa Markovin ketjuihin
- Osaat määritellä ja laskea ominaisarvojen algebrallisen ja geometrisen kertaluvut
- Osaat diagonalisoida matriisin käyttäen ominaisarvoja ja -vektoreita
Tällä viikolla näytämme sovelluksia ominaisarvoteoriasta, etenkin Markovin ketjuissa ja matriisien diagonalisoinnissa. Matriisien diagonalisointi on etenkin suurien matriisien tapauksessa hyvä tapa nopeasti laskea esimerkiksi potenssi käyttäen diagonaalimuotoa.
 Kuva: Sosiaalinen yhteistyöverkko eri ihmisten välillä. Tämän verkon voi esittää matriisina, jonka ominaisarvojen avulla voi esimerkiksi luokitella henkilöiden verkostointi linkkien määrän avulla. Samanlainen idea on taustalla Googlen PageRank algoritmin kanssa, jossa luodaan matriisi luokittelemaan internet sivujen merkittävyys. Kuva (c) Wikimedia Creative CommonsAktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):
Kuva: Sosiaalinen yhteistyöverkko eri ihmisten välillä. Tämän verkon voi esittää matriisina, jonka ominaisarvojen avulla voi esimerkiksi luokitella henkilöiden verkostointi linkkien määrän avulla. Samanlainen idea on taustalla Googlen PageRank algoritmin kanssa, jossa luodaan matriisi luokittelemaan internet sivujen merkittävyys. Kuva (c) Wikimedia Creative CommonsAktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 2-3 tuntia):- Video: Dynaamiset systeemit, ominaisarvoteoria ja matriisin potenssi (linkki)
- Video: Ominaisarvon algebrallinen ja geometrinen kertaluku (linkki)
- Video: Matriisin diagonalisointi ominaisarvoteorian avulla (linkki)
- Video: Matriisin potenssin laskeminen diagonalisoinnilla ja sovellus Google PageRank menetelmään (linkki, huom. Alussa kun laskimme A^2 ja A^k, unohtui kirjoittaa käänteismatriisi S^-1 tuon S sijaan oikealla puolella, esim pitäisi olla A^2 = S Λ^2 S^-1 eikä A^2 = S Λ^2 S.)
- Lue oppimateriaali (1-2 tuntia):
- Lue osiot 4.3, 4.4 ja 5.1 prujusta (Pruju materiaalit osiossa)
- Käsinkirjoitetut nootit videoilta (PDF alhaalla)
Torstain kertaussessio:
3. Osallistu kertaussessioon (1 tunti) Zoomissa:- Zoomissa Torstaina, kello 10:15-11:00, Zoom meeting ID 68625046500, linkki: https://aalto.zoom.us/j/68625046500, passcode: matriisi
- Kertaussession nauhoitus (linkki)
- Käsinkirjoitetut nootit kertaussessiosta (PDF alhaalla)
Aktiviteetit torstain kertaussession jälkeen:
4. Osallistu loppuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti
5. Tee ja palauta alkuviikon laskuharjoituksesi osiossa "Tehtävät" perjantaihin klo 17 mennessä.
6. Tee verkkotehtävät ensi viikon tiistaihin klo 17 mennessä.
7. Tee ja palauta loppuviikon laskaritehtävät ensi viikon tiistaihin klo 17 mennessä.
8. Itsearviointi. Arvioi oma opiskelusi. Minkä arvosanan antaisit itsellesi? Mitä olisi parannettavaa ratkaisuissasi? Mikä oli vaikeaa ja mikä helppoa? Oliko "ahaa"-elämyksiä?
-
Viikko 6. Unitaarinen diagonalisointi ja singulaariarvohajotelma
(18.10.2021 - 24.10.2021)Viikon oppimistavoitteet:
- Osaat unitaarisesti diagonalisoida normaalin matriisin
- Osaat laskea matriisin singulaariarvohajotelman (SVD)
VIimeisellä viikolla käymme läpi ns. normaalin matriisin unitaarisen diagonalisoinnin ja matriisin singulaariarvohajotelman (SVD). Erityisesti kvanttifysiikassa esiintyvät Gell-Mann matriisit ja kvanttitietokone malleissa esiintyvät Pauli matriisit ovat normaaleja. Osoittautuu, että normaalit matriisit voidaan aina diagonalisoida jopa unitaarisen matriisin avulla, joka on osa tärkeää normaalien matriisien spektraalilausetta, jota emme käsittele tällä kurssilla enempää. Yleisemmässä tapauksessa kun matriisi ei ole normaali tai jopa ei-neliömatriisi, voimme silti vielä muodostaa hyödyllisen matriisihajotelman, ns. singulaariarvohajotelman (SVD). Tämä metodi on erittäin hyödyllinen suuren datan analysoinnissa esimerkiksi koneoppimisessa ja tekoälyssä, liittyy niin sanottuun pääkomponenttianalyysiin (PCA) modernissa data-analyysissä, jossa pyrimme esittämään datasta keskeisimmät piirteet menettämättä oleellista informaatiota.
 Kuva: Singulaariarvohajotelman (SVD) sovellus kuvanpakkaukseen, jossa SVD säilyttää riittävän paljon informaatiota alkuperäisestä kuvasta mutta pienentää huomattavasti kuvan kokoa.Aktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 1-2 tuntia):
Kuva: Singulaariarvohajotelman (SVD) sovellus kuvanpakkaukseen, jossa SVD säilyttää riittävän paljon informaatiota alkuperäisestä kuvasta mutta pienentää huomattavasti kuvan kokoa.Aktiviteetit ennen torstain kertaussessiota:1. Osallistu alkuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti2. Opiskele viikon materiaali:- Katso videot (n. 1-2 tuntia):- Video: Unitaarinen diagonolisointi (linkki)
- Video: Esimerkki Pauli matriisin unitaarisesta diagonalisoinnista (linkki)
- Video: Matriisin singulaariarvohajotelma SVD (linkki)
- Video: SVD:n laskeminen (linkki)
- Video: Matriisin approksimaatio SVD:n avulla ja kohinan poistaminen datasta (linkki)
- Lue oppimateriaali (1-2 tuntia):
- Lue osiot 5.2, 5.3, 5.4 ja 5.5 prujusta (Pruju Materiaalit osiossa)
- Käsinkirjoitetut nootit videoilta (PDF alhaalla)
Torstain kertaussessio:
3. Osallistu kertaussessioon (1 tunti) Zoomissa:- Zoomissa Torstaina, kello 10:15-11:00 (mahdollisesti pitempään koska käytämme tällä kertaa erityisesti aikaa kokeen/tentin kannalta tärkeiden aiheiden kertaukseen), Zoom meeting ID 68625046500, linkki: https://aalto.zoom.us/j/68625046500, passcode: matriisi
- Kertaussession nauhoitus (linkki)
- Käsinkirjoitetut nootit kertaussessiosta (PDF alhaalla)
Aktiviteetit torstain kertaussession jälkeen:
4. Osallistu loppuviikon laskuharjoitusryhmääsi (2 tuntia). katso osio "Tehtävät" ryhmän aika ja sijainti
5. Tee ja palauta alkuviikon laskuharjoituksesi osiossa "Tehtävät" perjantaihin klo 17 mennessä.
6. Tee ja palauta loppuviikon laskaritehtävät ensi viikon tiistaihin klo 17 mennessä.
7. Itsearviointi. Arvioi oma opiskelusi. Minkä arvosanan antaisit itsellesi? Mitä olisi parannettavaa ratkaisuissasi? Mikä oli vaikeaa ja mikä helppoa? Oliko "ahaa"-elämyksiä?
8. Kertaa kokeeseen. Katso esimerkiksi "Kertausmateriaalia" kalvot Materiaalit osiossa prujun alapuolelta, tässä hyvin tiivistetty kaikki oleelliset asiat. Onnea kokeeseen!
-