Differentiaali- ja integraalilaskenta 2

Napakoordinaatit

Piste $(x,y)\in \mathbb{R}^2$ voidaan kirjoittaa muodossa $(r,\theta)$, missä $r\geq0$ ja $0\le \theta < 2\pi$. Napakulma $\theta$ on yksikäsitteinen jos $r > 0$.

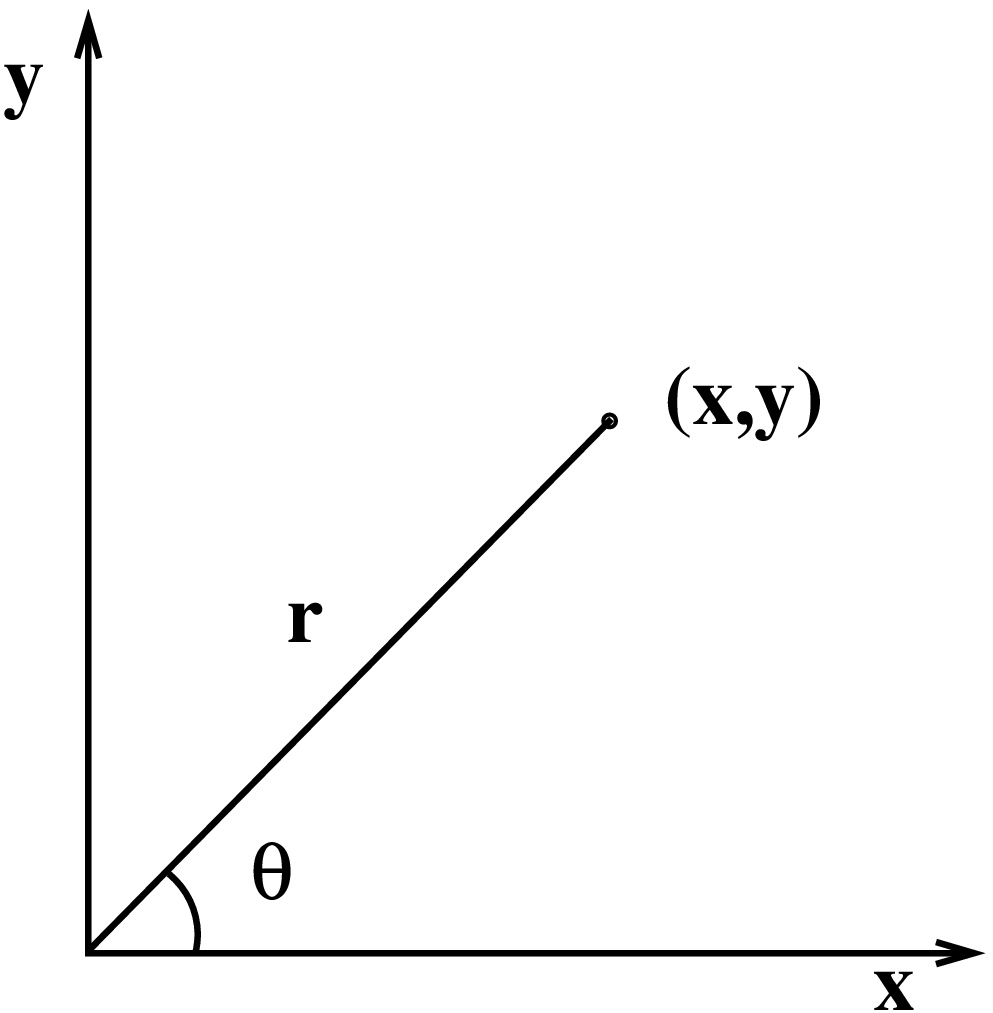
Alkeisgeometriasta saadaan kaavat $\left\{ \begin{array}{l} x=r\cos \theta\\ y=r\sin \theta \end{array}\right. \Leftrightarrow \left\{ \begin{array}{l} r^2=x^2+y^2 \\ \tan{\theta} = y/x. \end{array}\right.$ Vrt. kompleksiluvun polaarimuoto $x + i y = r e^{i \theta}$.

Koordinaatistomuunnoksen $(r, \theta) \mapsto (x,y)$ Jacobin determinantille saadaan kaava $\frac{\partial(x,y)}{\partial (r,\theta)} = \left|\begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array}\right| = \left|\begin{array}{cc} \cos \theta & -r\sin \theta\\ \sin \theta & r\cos\theta \end{array}\right| = r.$ Siten muuttujanvaihtokaavaa varten saadaan pinta-alan venytys $dx\,dy = \bigg|\frac{\partial(x,y)}{\partial (r,\theta)}\bigg| \,dr\,d\theta = r\,dr\,d\theta.$ Tasointegraali napakoordinaateissa $\iint_D f(x,y)\,dx\,dy = \iint_G g(r,\theta)r\,dr\,d\theta,$ missä $g(r,\theta) = f(r\cos\theta,r\sin\theta)$.

Esimerkki

(i) Olkoon $D=\lbrace (x,y)\in \mathbb{R}^2 : 1 < x^2 + y^2 < 4\rbrace$. Lasketaan napakoordinaateissa integraali $I=\iint_D \frac{1}{x^2+y^2}\,dx\,dy.$ Saadaan $I=\int_0^{2\pi}\int_1^2\frac{1}{r^2}r\,dr\,d\theta = \int_0^{2\pi} d\theta \cdot \int_1^2\frac{dr}{r} =2\pi\ln r\Big|_{r=1}^2 = 2\pi \ln 2.$

(ii) Integraali $\int_{-\infty}^\infty e^{-x^2}\,dx$ on erittäin tärkeä mm. todennäköisyyslaskennassa ja tilastotieteessä. Tämä integraali on vaikea, koska integraalifunktiota ei ole mahdollista kirjoittaa alkeisfunktioiden avulla.

Integraali on kuitenkin mahdollista laskea seuraavan tempun avulla: Huomataan aluksi, että $I = \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-x^2-y^2}\,dx\,dy = \bigg(\int_{-\infty}^\infty e^{-x^2}\,dx\bigg)^2.$ Laskemalla epäoleellinen tasointegraali napakoordinaateissa $I = \int_0^{2\pi}\int_0^\infty e^{-r^2}r\,dr\,d\theta = \int_0^{2\pi}d\theta \cdot \int_0^\infty r e^{-r^2}\,dr$ $= 2\pi \int_0^\infty{r e^{-r^2}\,dr} = -\pi \lim_{R \to \infty}{\int_0^R (-2r) e^{-r^2}\,dr}.$

Nyt $\frac{d}{dr} e^{-r^2} = -2r e^{-r^2}$, joten integraaliksi saadaan: $\int_0^R (-2r) e^{-r^2}\,dr = e^{-R^2} - 1$ Viemällä $R \to \infty$ tulee $I = \pi$ ja siitä alkuperäisen integraalin arvo $\int_{-\infty}^\infty e^{-x^2}\,dx = \sqrt{I} = \sqrt{\pi}.$ Miksi temppu toimi?

Muuttujanvaihto avaruusintegraalissa

Muunnoskaavat $(u,v,w) \mapsto (x,y,z)$ ovat $\left\{ \begin{array}{l} x=x(u,v,w),\\ y=y(u,v,w),\\ z=z(u,v,w). \end{array}\right.$ Tällöin $dx\,dy\,dz = \bigg|\frac{\partial(x,y,z)}{\partial (u,v,w)}\bigg|\,du\,dv\,dw,$ missä $\frac{\partial(x,y,z)}{\partial (u,v,w)} = \left|\begin{array}{ccc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w} \end{array}\right|.$ Jos siis $g(u,v,w) = f(x(u,v,w),y(u,v,w),z(u,v,w))$, niin $\iiint_D f(x,y,z)\,dx\,dy\,dz = \iiint_G g(u,v,w)\, \bigg|\frac{\partial(x,y,z)}{\partial (u,v,w)}\bigg|\,du\,dv\,dw.$

Sylinterikoordinaatit

Koordinaatit $(r,\theta,z)$, missä $r \geq 0$, $0\le \theta$, $z\in\mathbb{R}$. Suoralla $r = 0$ (eli $z$-akselilla) napakulma $\theta$ ei ole yksikäsitteinen.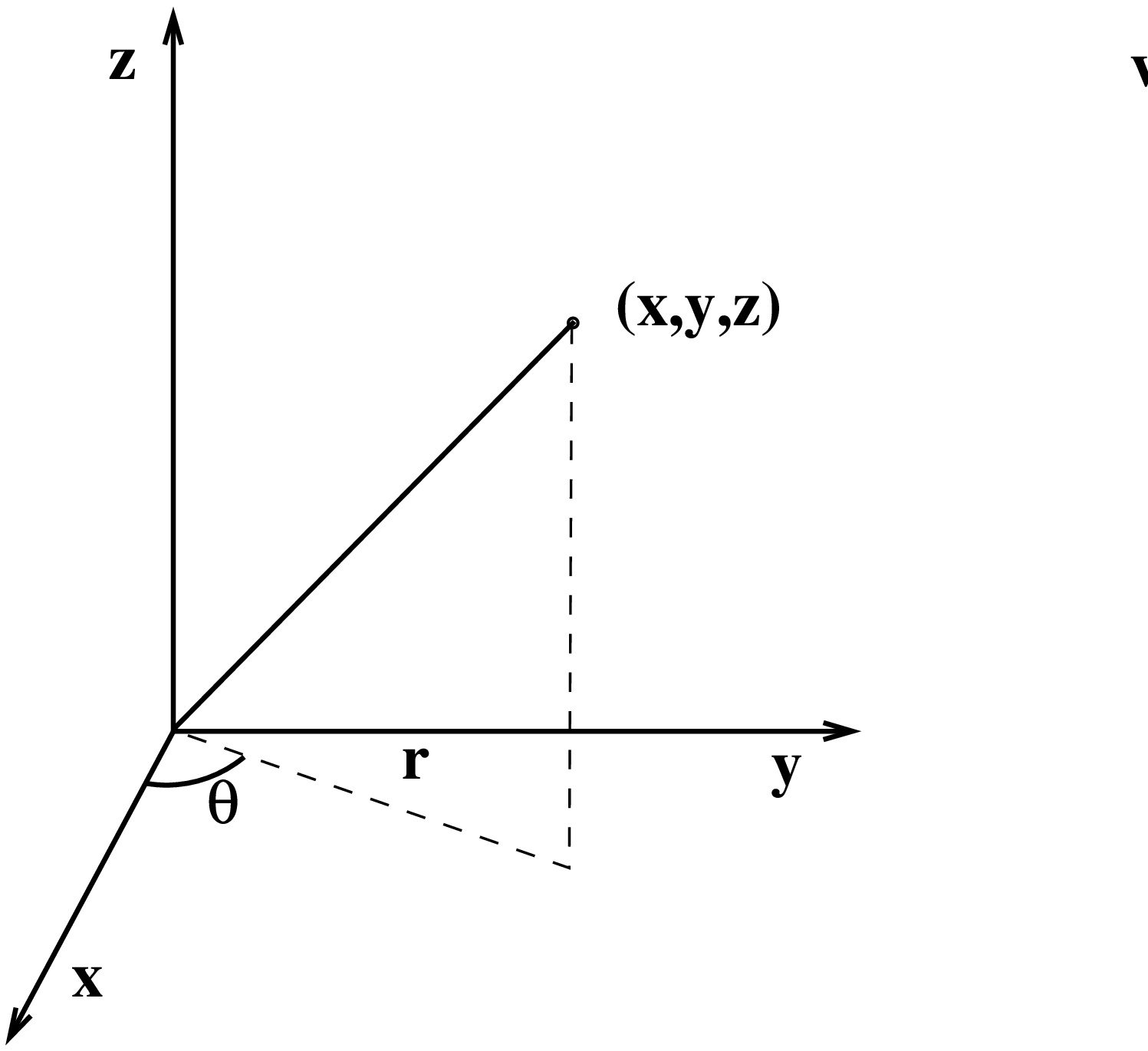

Tällöin muunnoskaavat $(r,\theta,z) \mapsto (x,y,z)$ ovat \begin{align*} \begin{cases} x &= r\cos\theta, \\ y &= r\sin\theta, \\ z &= z. \end{cases} \end{align*} Ja muunnoksen Jacobin determinantiksi saadaan $dx\,dy\,dz = \bigg|\frac{\partial(x,y,z)}{\partial (r,\theta,z)}\bigg|\,dr\,d\theta\,dz = r\,dr\,d\theta\,dz.$

Sylinterikoordinaateissa on helppo esittää pyörähdyskappaleita $z$-akselin ympäri muodossa $r = f(z), \quad \text{jossa} \quad z \in [a,b] \text{ ja } \theta \in [0, 2 \pi),$ missä $f$ on ei-negatiivinen funktio. Sylinterisymmetriset tehtävät!

Esimerkki

Lasketaan funktion $f$ määräämän pyörähdyskappaleen $\Omega$ tilavuus $\iiint_{\Omega} dx\, dy\, dz = \int_a^b\int_0^{2\pi}\int_0^{f(z)} r\,dr\,d\theta\,dz$ $= \int_a^b \left (2\pi \cdot \frac{1}{2}f(z)^2 \right ) \, dz = \pi \int_a^b f(z)^2 \, dz,$ mikä lienee tuttu kaava.

Pallokoordinaatit

Koordinaatit $(r,\theta,\phi)$, missä $r \geq 0$, $0\le \theta$, $0\le \phi \leq \pi$.

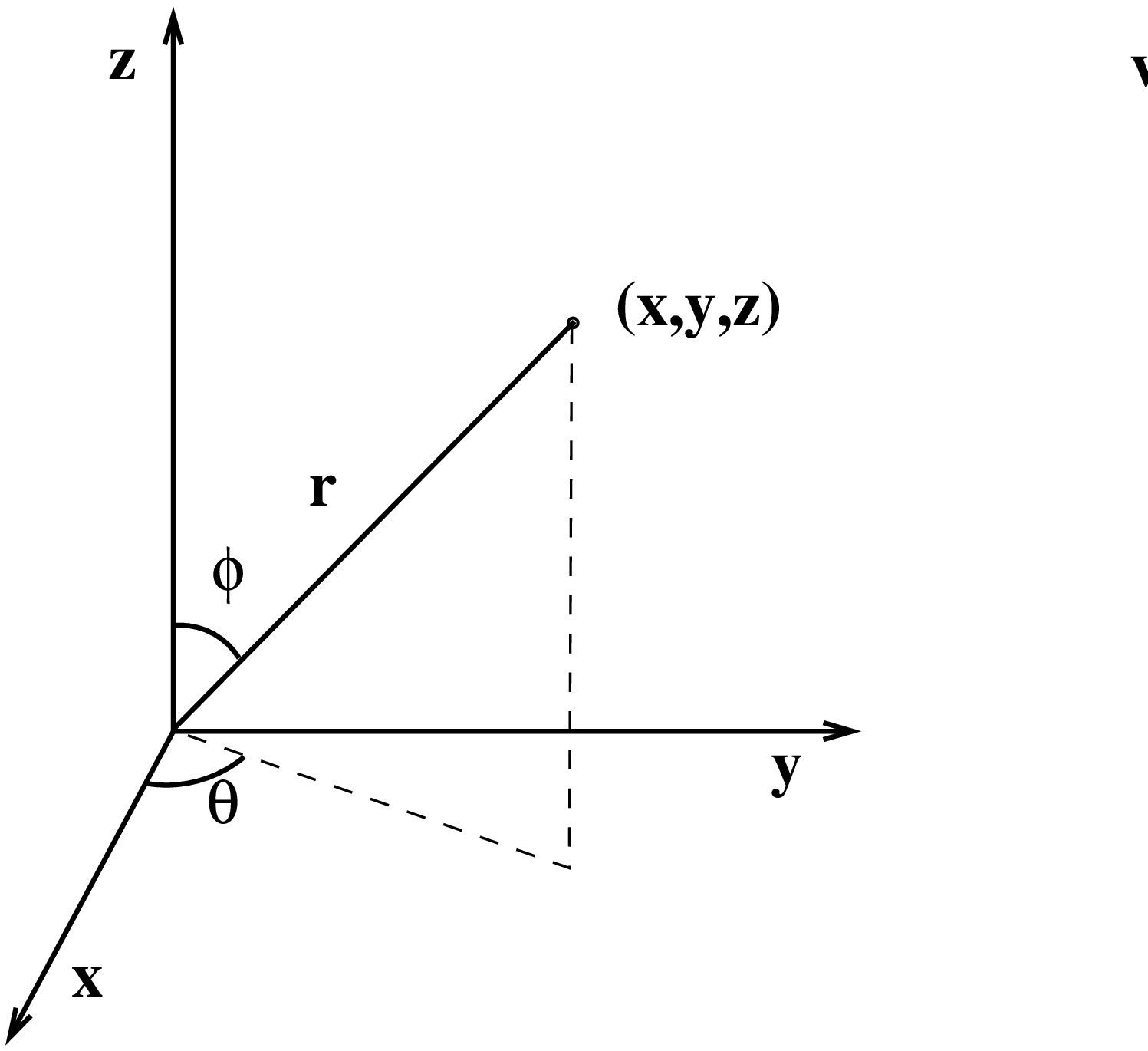
Korotus- eli napakulmaa $\pi/2 - \phi$ käytetään usein $\phi$:n sijasta. Atsimuuttikulma $\theta$ ja korotuskulma ovat yksikäsitteisiä, jos pisteen etäisyys $z$-akselista $> 0$. Muunnoskaavat ovat \begin{align*} \begin{cases} x&=r\sin\phi \cos\theta,\\ y&=r\sin\phi \sin\theta,\\ z&=r\cos\phi, \end{cases} \end{align*} ja muunnoksen Jacobin determinantiksi saadaan $dx\,dy\,dz = \bigg|\frac{\partial(x,y,z)}{\partial (r,\theta,\phi)}\bigg|\,dr\,d\theta\,d\phi = r^2\sin\phi \,dr\,d\theta\,d\phi.$

Esimerkki

Lasketaan $R$-säteisen pallon $\mathbb{B}^3(R)$ tilavuus: $V(\mathbb{B}^3) = \iiint_{\mathbb{B}^3(R)} 1\,dx\,dy\,dz = \int_0^R\int_0^{2\pi}\int_0^\pi r^2\sin\phi\,d\phi\,d\theta\,dr$ $= \int_0^R\int_0^{2\pi} -r^2\cos\phi\bigg|_{\phi=0}^\pi\,d\theta\,dr = \int_0^R\int_0^{2\pi} 2r^2\,d\theta\,dr$ $=\int_0^R 4\pi r^2\,dr = \frac{4\pi r^3}{3}\bigg|_{r=0}^R = \frac{4\pi R^3}{3}.$

Kaksiulotteinen pinta-ala avaruudessa

Tutkitaan kaksiulotteista kaareutuvaa pintaa $S$, joka on (piirtämisen helpottamiseksi) $xy$-tason yläpuolella avaruudessa $\mathbb{R}^3$.

Tarkastellaan aluksi $xy$-tason neliön yläpuolelle jäävän osan pinta-alaa. Se on ilmeisesti suurempi tai yhtäsuuri kuin vastaavan neliön pinta-ala.

Tästä johtuen pinta-aladifferentiaali $dS$ on suurempi tai yhtäsuuri kuin kuin $dx\,dy$. Itseasiassa $dx\,dy$ saadaan, jos $dS$ projisoidaan $xy$-tasoon. Projektio voidaan kirjoittaa kaavana $dx\,dy = \cos \gamma\,dS,$ missä $\gamma$ on pinnan $S$ normaalivektorin $\mathbf{N}$ ja $z$-akselin suuntaisen yksikkövektorin $\mathbf{k}$ välinen kulma. Toisaalta pistetulon määritelmästä saadaan $\mathbf{N} \cdot \mathbf{k} = \|\mathbf{N}\| \|\mathbf{k}\| \cos \gamma,$ ja siis $dS = \frac{1}{\cos \gamma}\,dx\,dy = \frac{\|\mathbf{N}\| \|\mathbf{k}\|}{\mathbf{N} \cdot \mathbf{k}}\,dx\,dy.$

Aikaisemmin on johdettu pinnan (ylöspäin suunnatulle) normaalivektorille esitys $\mathbf{N} = -\frac{\partial z}{\partial x}\mathbf{i} - \frac{\partial z}{\partial y}\mathbf{j} + \mathbf{k}.$ Saadaan $\|\mathbf{N}\| = \sqrt{1+ \Big(\frac{\partial z}{\partial x}\Big)^2 + \Big(\frac{\partial z}{\partial y}\Big)^2}$ Lisäksi $\|\mathbf{k} \| =1$ ja $\mathbf{N}\cdot \mathbf{k} = 1$, joten $dS = \sqrt{1+ \Big(\frac{\partial z}{\partial x}\Big)^2 + \Big(\frac{\partial z}{\partial y}\Big)^2}\,dx\,dy.$ Kaltevuuden huomioiva korjaustekijä yleistää tasointegraalin pintaintegraaliksi.

Esimerkki

Tarkastellaan sylinterin $x^2+y^2=a^2$, $a>0$ leikkaamaa palasta hyperbolisesta paraboloidista $z=x^2-y^2$. Mikä on palasen pinta-ala?

Lasketaan $\frac{\partial}{\partial x} z = 2x,\qquad \frac{\partial}{\partial y} z = -2y.$ Siten pinta-aladifferentiaaliksi saadaan $dS = \sqrt{1+ \Big(\frac{\partial z}{\partial x}\Big)^2 + \Big(\frac{\partial z}{\partial y}\Big)^2}\,dx\,dy$ $= \sqrt{ 1 + 4(x^2+y^2)} \,dx\,dy$ $=\sqrt{1+ 4r^2}\, r\,dr\,d\theta,$ napakoordinaateissa ilmaistuna.

Lasketaan nyt integraali napakoordinaateissa: $\textrm{Ala}(S)= \int_0^{2\pi} \int_0^a r\sqrt{1+4r^2}\,dr\,d\theta$ $= \frac{\pi}{4} \int_0^a 8r\sqrt{1+4r^2}\,dr$ $= \frac{\pi}{4} \bigg|_{r=0}^a\frac{2}{3}(1+4r^2)^{3/2} =\frac{\pi}{6} \big[(1+4a^2)^{3/2} -1\big].$