VERKKOKIRJA
7. Pinta-ala
Pinta-ala tasossa
Tarkastellaan umpinaisen ja itseään leikkaamattoman tasokäyrän raamien alueiden pinta-alaa. Pinta-alan yleinen käsite on teoreettisesti paljon hankalampi, mistä antaa viitteen luvun lopussa oleva huomautus.
Tasojoukon pinta-ala määritellään palauttamalla se yksinkertaisempien joukkojen pinta-aloihin. Erityisesti täytyy huomata, ettei pinta-alaa voi "laskea", ellei "pinta-alan" käsitettä ole ensin määritelty (vaikka koulumatematiikassa näin usein tehdäänkin).
Lähtökohta
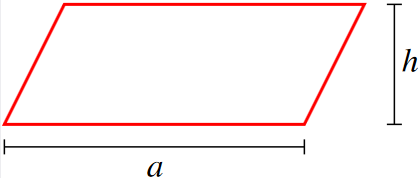
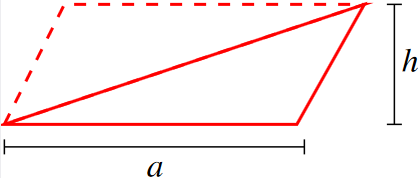
Monikulmio
(Yksinkertainen) monikulmio on tasojoukko, jota rajaa äärellisestä määrästä peräkkäisiä janoja koostuva suljettu käyrä. Vain peräkkäiset janat saavat leikata toisiaan yhteisessä päätepisteessä.
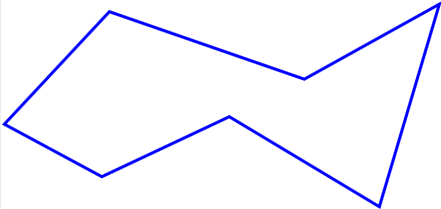
Määritelmä: Monikulmion pinta-ala
Monikulmion pinta-ala määritellään jakamalla se
äärelliseen määrään kolmioita (monikulmion
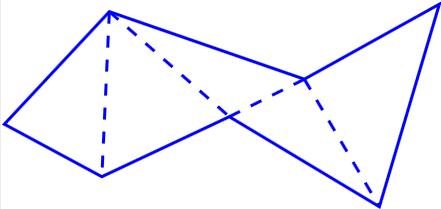
Lause.
Kolmioiden pinta-alojen summaf ei riipu monikulmion kolmioinnin valinnasta.
Yleinen tapaus
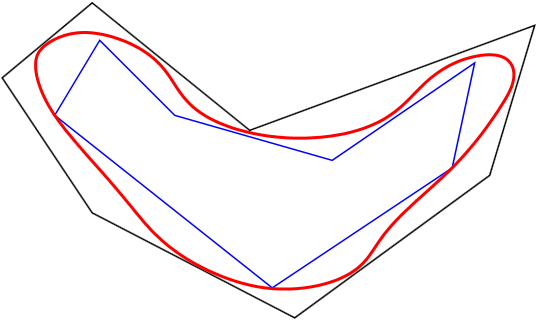
Tasojoukolle  , jota rajaa umpinainen itseään leikkaamaton käyrä, voidaan muodostaa
sisämonikulmioita
, jota rajaa umpinainen itseään leikkaamaton käyrä, voidaan muodostaa
sisämonikulmioita  ja ulkomonikulmioita
ja ulkomonikulmioita
 :
:  .
.
 on pinta-ala, jos jokaista
on pinta-ala, jos jokaista  vastaa sisämonikulmio
vastaa sisämonikulmio  ja ulkomonikulmio
ja ulkomonikulmio  , joiden pinta-alat poikkeavat toisistaan vähemmän kuin
, joiden pinta-alat poikkeavat toisistaan vähemmän kuin  :
:
 Tästä seuraa, että kaikkien lukujen
Tästä seuraa, että kaikkien lukujen  ja kaikkien lukujen
ja kaikkien lukujen  välissä on yksikäsitteinen luku
välissä on yksikäsitteinen luku  , joka on määritelmän mukaan joukon
, joka on määritelmän mukaan joukon  pinta-ala.
pinta-ala.
Yllätys: Se, että joukkoa  rajoittaa umpinainen (itseään leikkaamaton)
käyrä, ei takaa, että joukon pinta-ala on määritelty: Reunakäyrä voi olla niin "mutkitteleva",
että sillä on positiivinen "pinta-ala". Ensimmäisen esimerkin konstruoi [W.F. Osgood, 1903]:
rajoittaa umpinainen (itseään leikkaamaton)
käyrä, ei takaa, että joukon pinta-ala on määritelty: Reunakäyrä voi olla niin "mutkitteleva",
että sillä on positiivinen "pinta-ala". Ensimmäisen esimerkin konstruoi [W.F. Osgood, 1903]: