Differentiaali- ja integraalilaskenta 2
7. Taso- ja avaruusintegraalit
7.7. Epäoleelliset integraalit. Muuttujanvaihto taso- ja avaruusintegraaleissa
Epäoleelliset integraalit
Tähän asti integrointi on tapahtunut rajoitetussa alueessa rajoitetulle funktiolle (integrandille). Joskus voidaan kuitenkin integroida rajoittamattomia funktioita ja/tai rajoittamattomassa alueessa.
Tarkastellaan ainoastaan tapausta, jossa funktio  on ei-negatiivinen eli
on ei-negatiivinen eli  kaikilla
kaikilla  . Lasketaan funktion
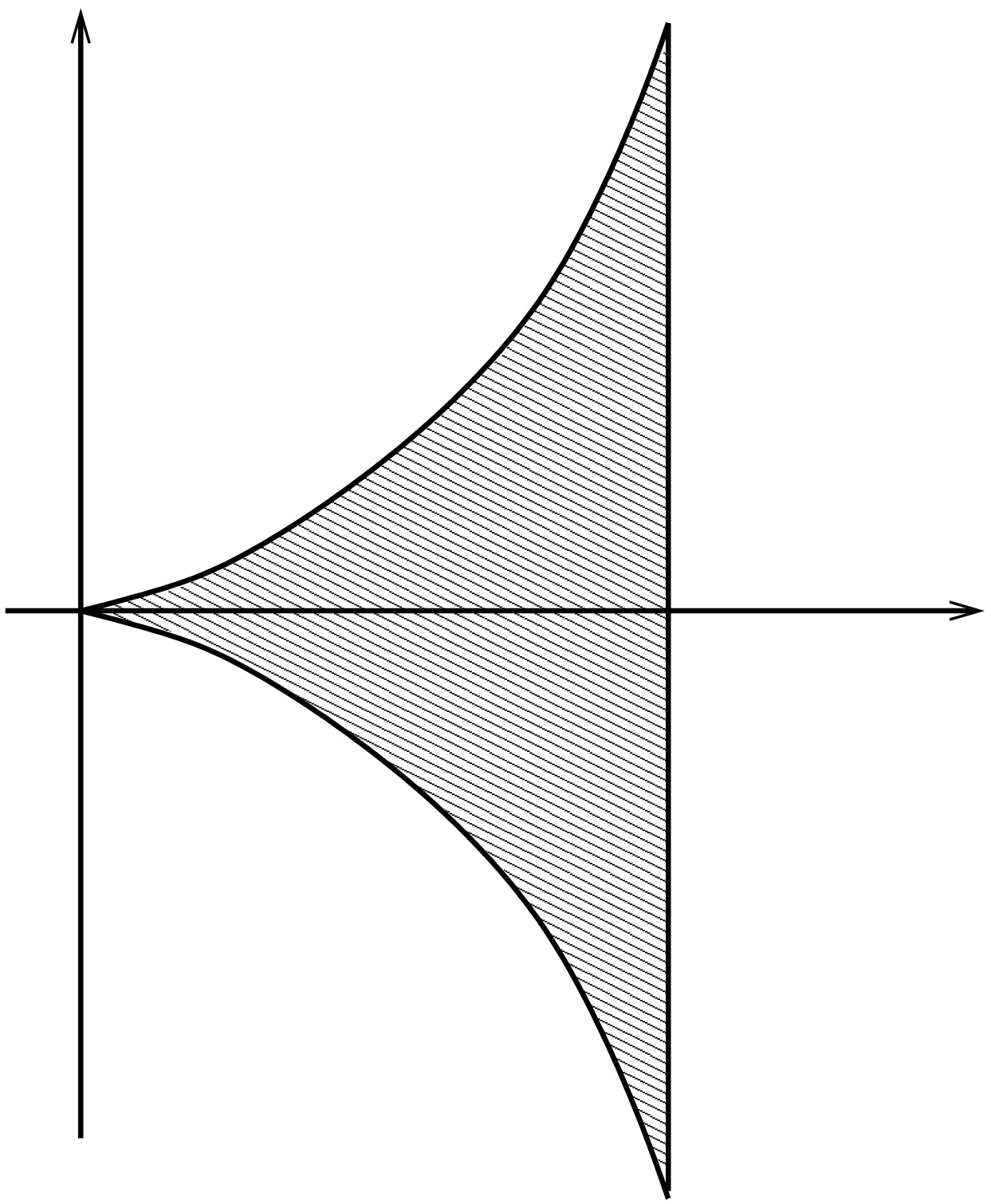
. Lasketaan funktion  integraali alueessa suorien
integraali alueessa suorien  rajoittamassa rajoittamattomassa alueessa
rajoittamassa rajoittamattomassa alueessa  , jossa
, jossa  . Mikäli integraali on suppenee, sen arvo saadaan laskemalla
. Mikäli integraali on suppenee, sen arvo saadaan laskemalla 
 Integraalin laskemiseksi huomataan, että
Integraalin laskemiseksi huomataan, että  . Siten
. Siten 
Esimerkki
Olkoon  ja rajoittamaton funktio
ja rajoittamaton funktio  .
.
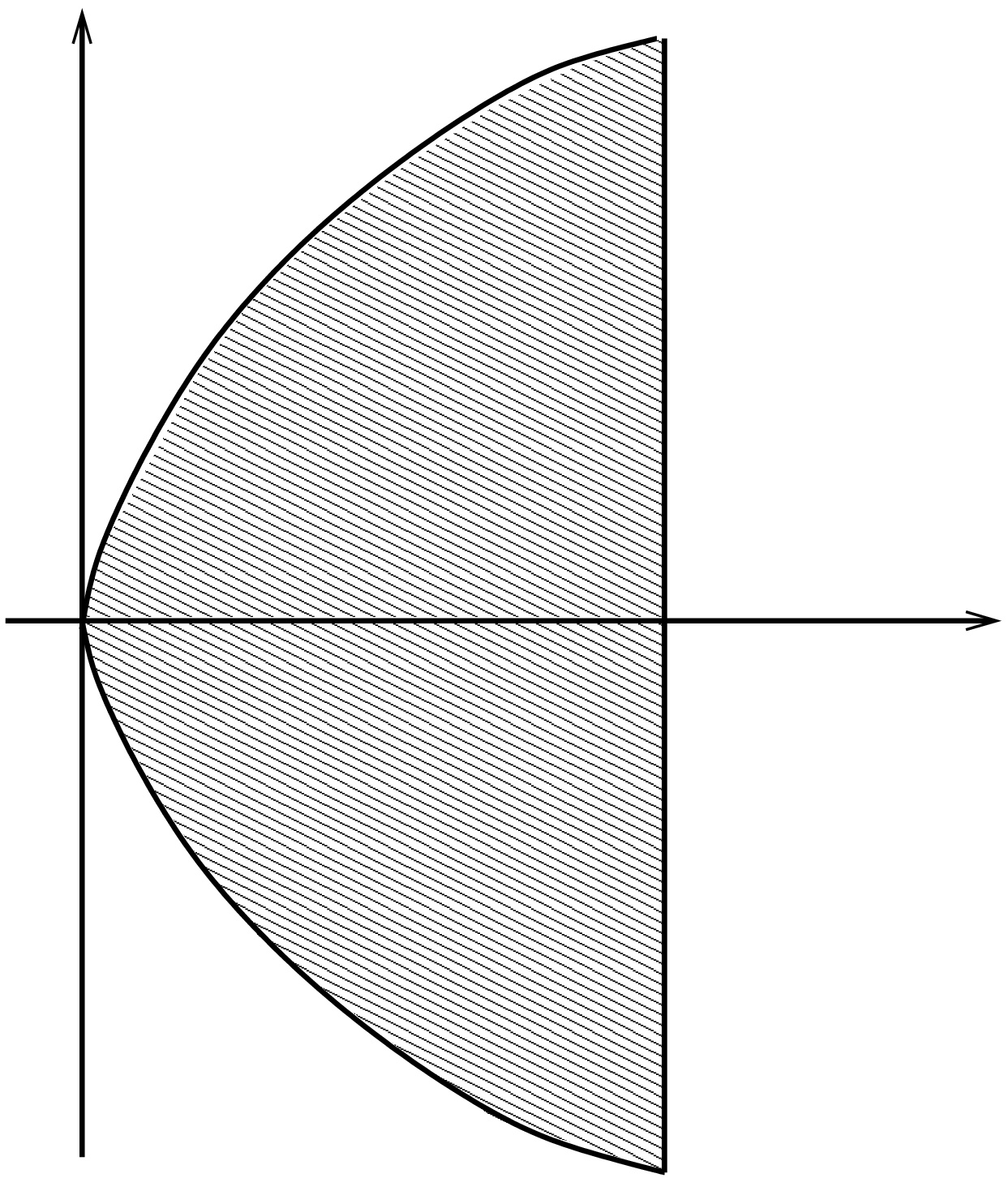
(ii) Lasketaan saman funktion integraali alueessa 

 Suppeneminen riippuu integroitavan funktion lisäksi myös alueesta!
Suppeneminen riippuu integroitavan funktion lisäksi myös alueesta!