Differentiaali- ja integraalilaskenta 2

Tasointegraali

Olkoon $D\subset \mathbb{R}^2$ joukko tasossa ja $f\colon D\to \mathbb{R}$ skalaarikenttä. Halutaan määritellä tasointegraali $\iint_D f(x,y)\,dA.$ Integraalin arvo on pinnan $z=f(x,y)$ ja $xy$-tason väliin jäävän alueen tilavuus.

Tutkitaan aluksi erikoistapausta $D=[a,b]\times [c,d]$.

Yhden muuttujan tapaus

Yhden muuttujan tapauksessa integraali saadaan Riemannin summien raja-arvona.

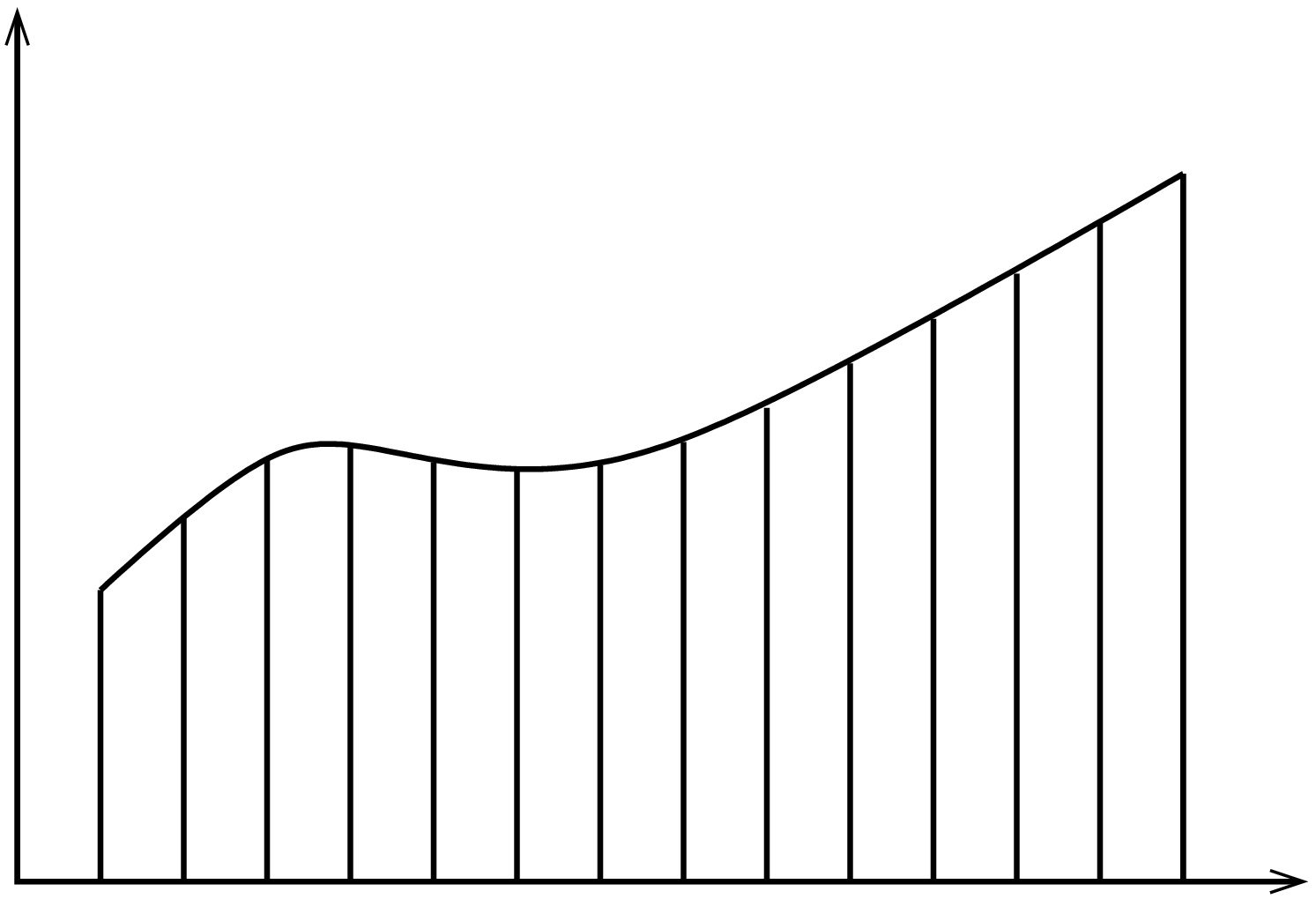
Formaalisti $\int_a^b f(x)\,dx = \lim_{n\to\infty} \sum_{i=1}^n f(x_i)\Delta x,$ missä $a=x_0 < x_1 < \ldots < x_n=b$ on välin $[a,b]$ tasavälinen jako ja $\Delta x$ on jakovälin pituus.

Usean muuttujan tapaus (tasointegraali, $\mathbb{R}^2$)

Jaetaan tason osajoukko $D=[a,b]\times [c,d]$ tasavälisesti ruudukoksi niin, että kummallakin akselilla on $n$ jakopistettä.

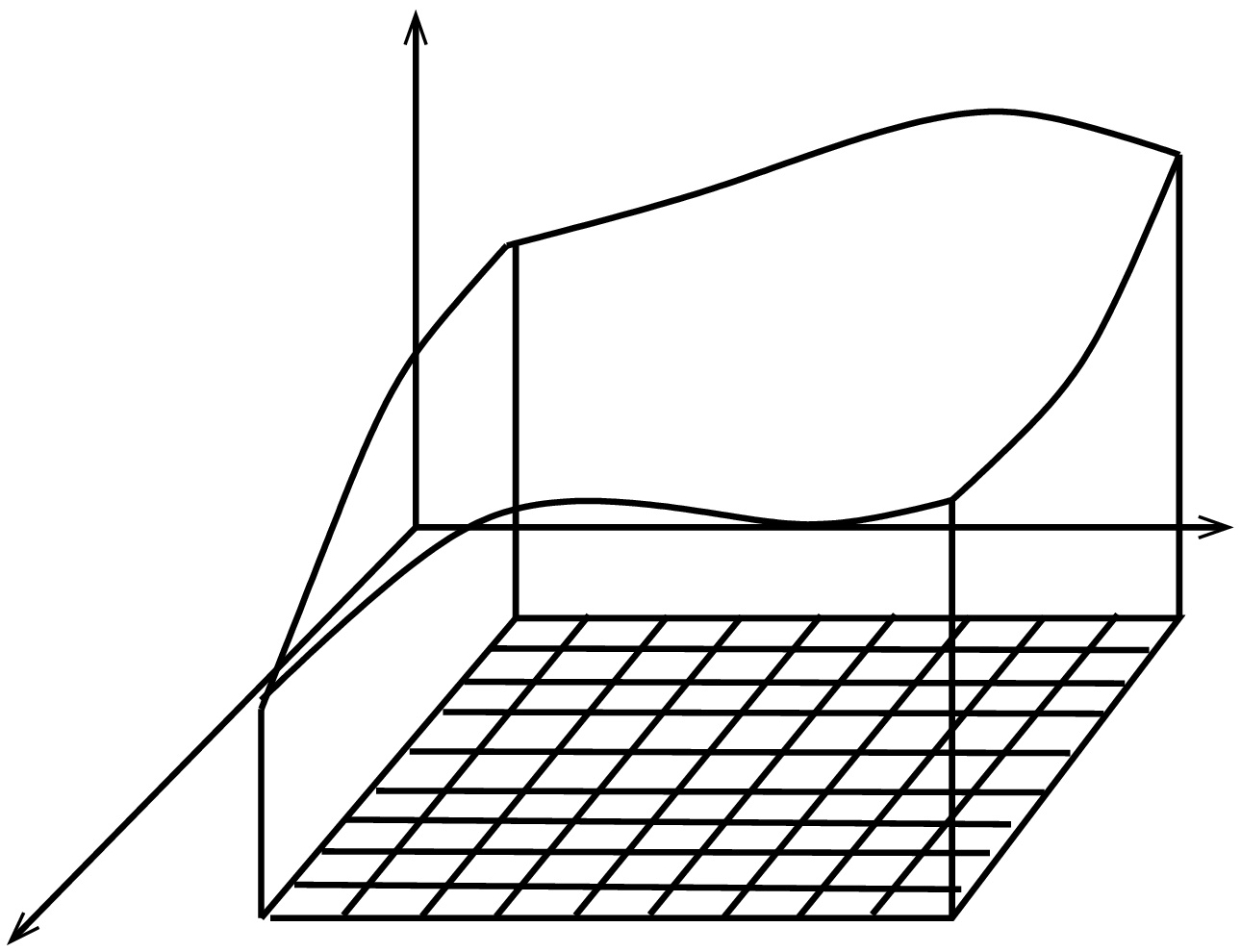
Nyt voidaan määritellä $\iint_D f(x,y)\,dA = \lim_{n\to\infty} \sum_{i=1}^n\sum_{j=1}^n f(x_i,y_j)\,\Delta x\Delta y,$ missä $x_{i} = a + i\frac{b-a}{n},\qquad y_{j} = c + j\frac{d-c}{n}$ ja $\Delta x$ sekä $\Delta y$ vastaavat jakovälien pituutta $x$ ja $y$-suunnassa: $\Delta x= \frac{b-a}{n},\quad \Delta y = \frac{d-c}{n}.$

Huomautuksia

Yhden muuttujan tapauksessa integraaleille pätee Analyysin (ensimmäinen) peruslause: $f(x)=\frac{d}{dx}\int_c^x f(t)\,dt,\textrm{ kun }c,x\in[a,b]$ ja $f\colon [a,b]\to\mathbb{R}$ on jatkuva funktio.

Analyysin peruslauseesta seuraa, että integrointi ja derivointi ovat toistensa vastaoperaatiota, mikä johtaa moniin integroinnissa hyödyllisiin kaavoihin. Analyysin peruslauseella ei kuitenkaan ole aivan samanlaista vastinetta usean muuttujan tapauksessa; Greenin, Gaussin ja Stokesin lauseet ovat kuitenkin sille sukua.

Moninkertainen integraali

Monen muuttujan integraaleja voidaan usein kuitenkin laskea moninkertaisina integraaleina. Kaksiulotteinen tapaus (integrointialue suorakulmio) $\iint_D f(x,y)\,dA = \int_c^d \int_a^b f(x,y)\,dx\,dy, \text{ kun } D=[a,b]\times [c,d].$

Mikäli funktio $f\colon \mathbb{R}^2 \to \mathbb{R}$ on jatkuva, niin integroimisjärjestyksellä ei ole väliä integraalin arvon kannalta. Laskujen helppouden kannalta väliä kuitenkin on.

Esimerkki

Olkoon $f(x,y)=xy^2$. Lasketaan $\iint_D f(x,y)\,dA,\text{ kun } D=\{(x,y)\in \mathbb{R}^2: 0\le x\le1, \,0\le y\le 1\}.$
Aluksi kirjoitetaan tasointegraali kaksinkertaisena integraalina, ja lasketaan \begin{align*} \iint_D xy^2\,dA &= \int_0^1\int_0^1 xy^2\,dx\,dy = \int_0^1\bigg[\frac{x^2y^2}{2}\bigg]_{x=0}^{1}\,dy \\ &= \int_0^1 \frac{y^2}{2}\,dy \bigg[\frac{y^3}{6}\bigg]_{y=0}^1 = \frac{1}{6}. \end{align*}

Integrointi yleisemmissä alueissa

Tutkitaan funktiota $f\colon D\to \mathbb{R}$, joka on määritelty tason osajoukossa $D$. Tähän asti on oletettu, että $D$ on suorakulmio. Yleisemmässä tapauksessa voidaan tarkastella suorakulmiota $\hat D$, jolle $D\subset \hat D$. Jotta integraali olisi määritelty, täytyy joukon $D$ olla ''siisti'' (riittää esimerkiksi, että reuna on paloittain sileä).

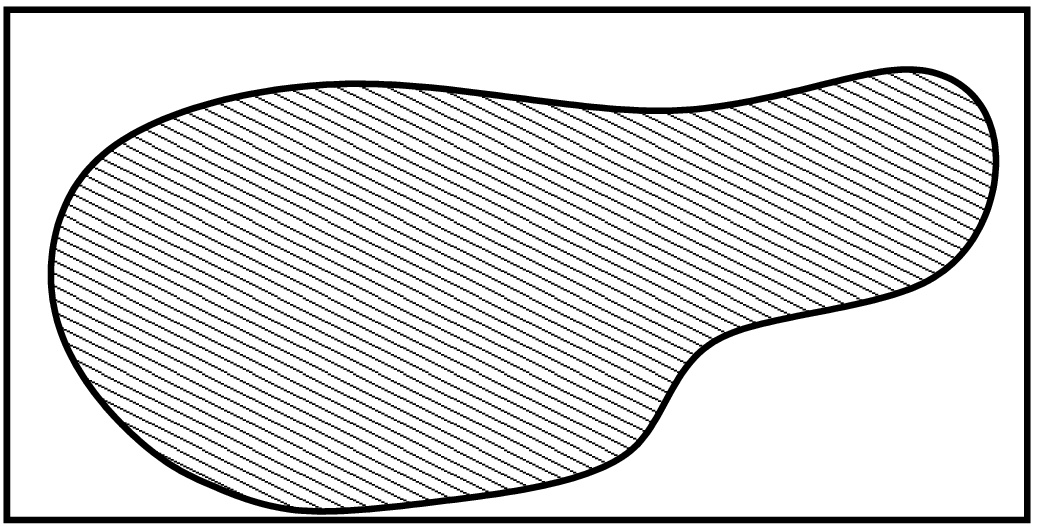
Määritellään funktio $\hat f\colon \hat D \to \mathbb{R}$ seuraavasti: $\hat f(x,y) = \left\{ \begin{array}{rcl} f(x,y), &\text{kun} &(x,y) \in D,\\ 0, & \text{kun} & (x,y) \in \hat D \setminus D. \end{array}\right.$ Nyt voidaan määritellä $\iint_D f(x,y)\,dA := \iint_{\hat D} \hat f(x,y)\,dA.$ Samaan tapaan voidaan määritellä myös avaruusintegraali ei-suorakulmaisen integroimisalueen tapauksessa: $\iiint_D f(x,y,z)\,dV := \iiint_{\hat D} \hat f(x,y,z)\,dV,$ kun $\hat D$ on suorakulmainen särmiö ja $D \subset \hat D$.

Esimerkki

Olkoon $D=\{(x,y)\in \mathbb{R}^2 : 0 < x < 1,\, 0 < y < x\}$. Lasketaan funktion $f(x,y)=xy$ integraali yli alueen $D$.

\begin{align*} &\iint_D xy\,dA = \int_0^1\bigg(\int_0^x xy\,dy\bigg)dx \\ &\quad \int_0^1\frac{xy^2}{2}\bigg|_{y=0}^x\,dx = \int_0^1\frac{x^3}{2}\,dx = \frac{x^4}{8}\bigg|_{x=0}^1 =\frac{1}{8}. \end{align*} Integrointi on mahdollista suorittaa myös toisessa järjestyksessä: \begin{align*} &\iint_D xy\,dA = \int_0^1\bigg(\int_y^1 xy\,dx\bigg)dy \\ &\quad = \int_0^1\frac{x^2y}{2}\bigg|_{x=y}^1\,dy = \int_0^1\frac{y}{2}-\frac{y^3}{2}\,dy \\ &\quad = \bigg[\frac{y^2}{4}-\frac{y^4}{8}\bigg]_{y=0}^1 = \frac{1}{4}-\frac{1}{8} = \frac{1}{8}. \\ \end{align*}

Esimerkki

Lasketaan funktion $f(x,y)=e^{x^2}$ integraali edellisen esimerkin alueessa.

$\iint_D e^{x^2}\,dA = \int_0^1\bigg(\int_0^x e^{x^2}\,dy\bigg)dx =\int_0^1 xe^{x^2}\,dx$ Sijoituksella $t=x^2$, $dt=2x\,dx$ saadaan $\frac{1}{2}\int_0^1e^t\,dt = \frac{1}{2}e^t\bigg|_{t=0}^1 = \frac{e}{2}-\frac{1}{2}.$