Python-oppimateriaali (CHEM-A2600)

scipy.integrate.solve_ivp

Kemian tekniikassa haluamme usein ratkaista (integroida) differentiaaliyhtälöitä numeerisesti. SciPyn integrate-alamoduuli sisältää useita funktioita tätä varten. Tällä kurssilla tutustutaan scipy.integrate.solve_ivp-funktioon. Funktion solve_ivp käyttötarkoitus on: "Solve an initial value problem for a system of ordinary differential equations", eli kysessä on alkuarvotehtävän numeerinen ratkaisumenetelmä. Aiemmin alkuarvotehtävien ratkaisemiseen oli käytettävissä scipy.integrate.odeint-funktio, mutta nykyisin Scipyn kehittäjät suosittelevat hyödyntämään solve_ivp-funktiota.

Käydään läpi klassinen esimerkki, eli bakteeripopulaation eksponentiaalinen kasvu. Esimerkkisysteemimme osalta tiedetään, että bakteeripopulaation kasvunopeus dy/dt on suoraan verrannollinen populaation kokoon y ajan hetkellä t:

dy/dt = k * y

Tässä tapauksessa differentiaaliyhtälö on itse asiassa hyvin helppo ratkaista analyyttisesti suoralla integroinnilla (ks. Wikipedia-sivu). Mutta havainnollistetaan tämän suoraviivaisen esimerkin avulla, kuinka differentiaaliyhtälön numeerinen integrointi onnistuu SciPyllä.

Aja alla oleva esimerkki Spyderissä.

Huomaa, miten dy/dt on määritelty funktiona f_dy_dt ja miten tämä funktio annetaan solve_ivp-funktion parametriksi.
Lisäksi solve_ivp saa parametrina muuttujan y (bakteeripopulaatio) alkuarvon y_0 ja tutkittavat ajanhetket taulukossa t_eval.
Käytännössä siis solve_ivp siis kutsuu funktiota f_dy_dt eri ajan hetkillä t, jolloin bakteeripopulaation koko on y.

import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate

k = 0.92  # kasvunopeus
y_0 = np.array([500]) # bakteeripopulaatio alussa

def f_dy_dt(t, y):
    # Differentiaaliyhtälön määritelmä eksponentiaaliselle kasvulle
    # Parametri y on populaatio ajan hetkellä t
    # Huomaa, että aikaparametria t ei tarvita tässä tapauksessa, mutta 
    # funktion määritelmän täytyy sisältää se
    dy_dt = k * y
    return dy_dt

# Simuloidaan ajanhetket t = [0, 4] h
max_t = 4 # tuntia
t = np.linspace(0, max_t, max_t * 4 + 1) # pisteet 0.25 h välein

# Differentiaaliyhtälön numeerinen integrointi
# fun    -> Differentiaaliyhtälön dy/dt = f(t, y) oikea puoli.
# t_span -> Differentiaaliyhtälön numeerisen integroinnin alku- ja loppupiste.
# y0     -> Alkuarvot, eli bakteeripopulaatio alussa. Yksiulotteinen NumPy-taulukko.
# t_eval -> Ajanhetket, joissa bakteeripopulaatio lasketaan funktion f_dy_dt avulla. Yksiulotteinen NumPy-taulukko.
# Paluuarvo on ns. olio, joka sijoitetaan muuttujaan "tulos" (olioista kerrotaan lisää luvussa 7). 
# Nyt meille riittää tieto, että voimme hyödyntää paluuarvoa seuraavalla tavalla:
#     tulos.t    -> ajanhetket, yksiulotteinen NumPy-taulukko
#     tulos.y[0] -> Bakteeripopulaation määrä kullakin ajanhetkellä, yksiulotteinen NumPy-taulukko
tulos = scipy.integrate.solve_ivp(fun = f_dy_dt, 
                                  t_span = (t[0], t[-1]), 
                                  y0 = y_0, 
                                  t_eval = t)

# Piirretään kuvaaja
teksti = f"Bakteeripopulaatio (k = {k:.2f}, y_0 = {y_0[0]:d})"
plt.plot(tulos.t, tulos.y[0], color = 'red', label = teksti)
plt.xlim(0, max_t)
plt.ylim(0.0, 20000)
plt.xticks(np.linspace(0.0, 4.0, num = 9))
plt.yticks(np.arange(0, 20001, 2000))
plt.xlabel('t (h)')
plt.ylabel('Bakteeripopulaatio')
plt.legend(loc = 'upper left', frameon = False)
plt.show()

Lopputuloksena on seuraavan näköinen kuvaaja:

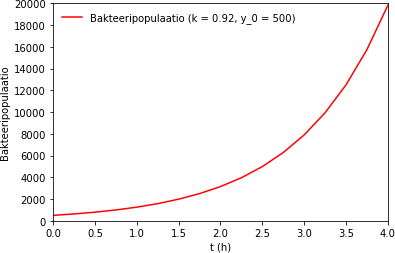
Huomaa, että solve_ivp-funktion parametri y0 voi olla myös vektori. Tällöin myös derivaatat laskeva funktio saa parametrikseen vektorin y ja solve_ivp palauttaa taulukon tulos.y, jossa on yhtä monta riviä kuin vektorissa y0 on alkioita.

Python-oppimateriaali (CHEM-A2600)

scipy.integrate.solve_ivp

Tehtävä 6.5.1