Kirja
1. Electrochemical system
1.2. Electrochemical reaction
An electrochemical reaction involves always electron transfer between species. Such a reaction is called a redox reaction. It is defined:
Oxidation means donating an electron and reduction accepting an electron. |
|---|
A substance capable of oxidizing another substance is knows as an oxidant. Accordingly, a reducing
substance is a reductant. If we
write down a reaction
| Aox + Bred → Ared + Box , | (1.1) |
|---|
where n electrons are transferred from B to A, A is the oxidant of B and B is the reductant of A. Hereinafter in this book, the subscripts ’ox’ and ’red’ refer to the oxidized and reduced species, respectively.
The ability of a substance to oxidize or reduce another substance depends on their electron structure and, to a lesser extent, on the medium. This ability is reflected in the values of the standard reduction potentials that are tabulated for several elements and molecules. Standard potentials are discussed in Chapter 4, and a selection of the most common redox couples is given in Appendix 6. From the standard potentials it is possible to deduce which reactions would occur spontaneously or how much energy must be fed in to the system to force a reaction to take place.*
If an electron transfers from a species in the solution to another species without a mediating electrode, electron transfer is homogeneous. For example, if an aqueous solution of CeCl4 and FeCl2 are shaken for a while, Ce4+ oxidizes Fe2+ to Fe3+ reducing to Ce3+. In biology, redox reactions are mostly homogeneous. Metals can also be reduced from aqueous solutions with strong reductants without an external circuit. One of the best known processes is the deposition of nickel from a hypophosphate solution. This kind of processes are known as electroless plating. They do not, however, represent true homogeneous electron transfer because a solid surface mediates electrons and other simultaneous reactions compensate the transferred charges.
A redox reaction is electrochemical if electron transfer takes place heterogeneously, most commonly on solid electrodes.
Electrochemical reaction is a heterogeneous redox reaction. |
|---|
An alternative definition would be
Rate of an electrochemical reaction depends on potential. |
|---|
Electrodes traditionally used in electrochemistry are made of solid materials that have sufficient electrical conductivity, such as metals, graphite or indium-titan oxide glass (ITO). An electrode exchanges an electron with a reacting species, and receives an electron from an external circuit or donates an electron to it. The surface of an electrode can be modified with functional groups in order to enhance its selectivity towards a particular reacting species.
As a result of a redox reaction, an imbalance of charges is created in the solution, and another electrode must be inserted in the system to maintain electroneutrality in the solution. The electrodes must be connected via an external circuit. Reaction (1.1) can now be written in terms of electrode reactions as follows:
| Aox + ne– → Ared reduction
at the cathode |
(1.2a) |
|---|---|
| Bred → Box+ ne– oxidation at the anode | (1.2b) |
Summing reactions (1.2a) and (1.2b) gives reaction (1.1). In reaction (1.2a) the electrode donates n electrons to Aox: it is a cathode. In reaction (1.2b) the other electrode receives the same number of electrons: it is an anode.
Reactions (1.2) and (1.2b) are the half-reactions of reaction (1.1). If we want to study, say, the rate of the half-reaction (1.2a), the cathode is called the working electrode, and the anode that only balances the number of charges in the solution the counter electrode or the reference electrode. In modern electrochemical measurement, the counter and reference electrodes are separate – this will be discussed in Chapter 4.7.
Electron transfer is a fundamental reaction which is very difficult to describe with quantum mechanics. Theories of electron transfer have traditionally been based on the famous Arrhenius equation or the absolute rate theory (aka theory of activated complexes) by Eyring. The rate of electron transfer, in other words electric current, is, however, easily measured and controlled in situ, making electrolysis a widely used chemical process.
1.2.1 Cell voltage due to an electrochemical reaction
Let’s write down a very simple and familiar reaction:
| H2(g) + ½ O2(g) → H2O(l) | (1.3) |
|---|
It is found from thermodynamic
tables that the standard Gibbs free energy of the reaction is  G0 = –237 kJ mol–1. The reaction does not appear electrochemical
but it is the net reaction of the hydrogen fuel cell in acidic conditions. At
the anode of the fuel cell, hydrogen decomposes by means of a catalyst (oxidizes):
G0 = –237 kJ mol–1. The reaction does not appear electrochemical
but it is the net reaction of the hydrogen fuel cell in acidic conditions. At
the anode of the fuel cell, hydrogen decomposes by means of a catalyst (oxidizes):
| H2 → 2 H+ + 2 e– | (1.4) |
|---|
Protons are transported to the cathode through the electrolyte and electrons via the external circuit. At the cathode, oxygen is reduced:
| ½ O2 + 2 H+ + 2 e– → H2O | (1.5) |
|---|
The sum of reactions (1.4) and (1.5) is reaction (1.3). What does this mean? The homogeneous reaction (1.3) has been split into two heterogeneous electrode reactions. The cell voltage is defined as follows:
 |
(1.6) |
|---|
Two electrons are transported per water molecule. Hence, the standard cell voltage (or potential) is
the thermodynamic (= equilibrium) potential of the hydrogen fuel cell**.
Thus, in
electrochemistry, a homogeneous reaction is split into two heterogeneous reactions
and the Gibbs free energy of the reaction,  G, is harnessed as electrical energy. In a reverse process, electrical energy
can be used to run reactions against their natural affinity. The question of how
G, is harnessed as electrical energy. In a reverse process, electrical energy
can be used to run reactions against their natural affinity. The question of how  G of the total reaction is split between the
half-reactions remains still unanswered. As will be seen in Chapter 4, thermodynamics
is incapable of answering this question, but it is resolved with an IUPAC
resolution. This does not actually matter because measuring a single electrode
potential, i.e. its energy, is not possible, only the potential difference between two electrodes can be measured.
G of the total reaction is split between the
half-reactions remains still unanswered. As will be seen in Chapter 4, thermodynamics
is incapable of answering this question, but it is resolved with an IUPAC
resolution. This does not actually matter because measuring a single electrode
potential, i.e. its energy, is not possible, only the potential difference between two electrodes can be measured.
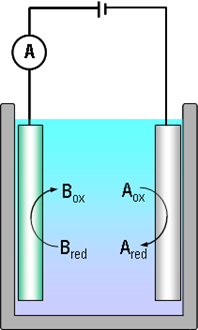
1.2.2 Electric current due to an electrochemical reaction
Consider electric current with the help of reactions (1.2) and Figure 1.1. The electrons that Bred donates to the anode are transported to the cathode via the external circuit, making the measurement of current feasible. Because the rate at which Bred donates the electrons is equal to the rate at which Aox receives them and that is equal to the electron flux in the external circuit, electric current is proportional to the reaction rate. This fundamental notion is known as Faraday's law: |
(1.7) |
|---|
where i is electric current density (A cm–2), n the number of electrons exchanged in the reaction, F the Faraday constant (96485 As mol–1) and r the reaction rate (mol cm–2 s–1). The direction of electric current is defined as the direction of positive current, i.e. opposite to the direction of electrons. In a solution, the current flows in the direction of the positively charged species. When representing current-voltage curves in x-y coordinates, it is still necessary to agree if an oxidation or reduction current is positive: according to the IUPAC resolution, an oxidation current is positive. Many text books, however, especially ones about polarography, show cathodic current (reduction current) as positive. Great care must therefore be taken when reading literature and noticing the sign convention used by authors.
It is necessary to emphasize that an electrochemical reaction is the only reaction, the rate of which can be measured in situ. With modern current amplifiers, the measurement of pA (10–12 A) currents is rather easy. Applying the Faraday law it is simple to calculate that this corresponds to the transfer of the order of 106 electrons per second.
Since electric current is a property of a closed circuit, its magnitude depends on the rate of the slower reaction. Let’s assume that the reduction reaction (1.2a) is faster than the oxidation reaction (1.2b). If the electrodes in Fig. 1.1 are short-circuited, electric current density is i = nFrox because the rate of the oxidation reaction limits the rate of electron flow. Superficially thinking, this observation may seem self-evident but it has a huge impact in the production of metals via electrolysis where oxygen evolution is the anode reaction. The rate of oxygen evolution (inverse of reaction (1.5)) is limited by reaction kinetics, increasing the cell voltage by several hundred millivolts which, in turn, increases the energy cost of the process significantly.
* Standard potentials are thermodynamic quantities, but sometimes reaction kinetics determines which reaction prevails in the system. The electrolysis of zinc is a famous example of the kinetic control.
**Note that J = VAs
