VERKKOKIRJA
| Site: | MyCourses |
| Course: | MS-A0103 - Differentiaali- ja integraalilaskenta 1 (ELEC1, ENG1), Luento-opetus, 4.9.2023-18.10.2023 |
| Book: | VERKKOKIRJA |
| Printed by: | Guest user |
| Date: | Wednesday, 19 February 2025, 12:30 AM |
Description
Differentiaali- ja integraalilaskenta - verkkokirja, tekijä Pekka Alestalo
Englanninkielisen MOOC-kurssin luentomateriaali, joka perustuu tämän kurssin luentoihin. Mukana on interaktiivisia JSXGraph-kuvia, joita ei ole suomenkielisissä luentokalvoissa. Toistaiseksi vain luvut 1-5, 7 ja 9 ovat suomeksi.
1. Jonot
Sisältö
- Peruskäsitteet
- Tärkeitä jonoja
- Suppeneminen ja raja-arvo
Jonot
Tämä luku sisältää tärkeimmät jonoihin liittyvät käsitteet. Käsittelemme käytännössä vain reaalilukujonohin liittyviä asioita.
Huom. Koska  on järjestetty joukko, niin myös jonon termeillä
on järjestetty joukko, niin myös jonon termeillä  on vastaava järjestys. Sen sijaan joukon alkioilla ei yleisessä tapauksessa
ole määrättyä järjestystä.
on vastaava järjestys. Sen sijaan joukon alkioilla ei yleisessä tapauksessa
ole määrättyä järjestystä.
Määritelmä: Jonon termit ja indeksit
Jonoille voidaan käyttää myös merkintöjä
Funktion  perusteella jokaiseen jonon termiin liittyy yksikäsitteinen lukua
perusteella jokaiseen jonon termiin liittyy yksikäsitteinen lukua  to each term. Se merkitään alaindeksinä ja sitä kutsutaan vastaavan jonon termin
indeksiksi; jokainen jonon termi voidaan siis tunnistaa sen indeksin avulla.
to each term. Se merkitään alaindeksinä ja sitä kutsutaan vastaavan jonon termin
indeksiksi; jokainen jonon termi voidaan siis tunnistaa sen indeksin avulla.
Esimerkkejä
Esimerkki 1: Luonnollisten lukujen jono
Jono  , joka on määritelty kaavalla
, joka on määritelty kaavalla  on nimeltään luonnollisten lukujen jono. Sen ensimmäiset termit ovat:
on nimeltään luonnollisten lukujen jono. Sen ensimmäiset termit ovat:

![]()
Esimerkki 2: Kolmiolukujen jono
Kolmioluvut saavat nimensä seuraavasta geometrisesta periaatteesta: Asetetaan sopiva määrä kolikoita niin, että syntyy yhä suurempia tasasivuisia kolmioita:
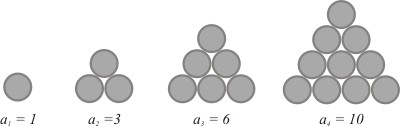
Ensimmäisen kolikon alle lisätään kaksi kolikkoa, jolloin toisessa vaiheessa saadaan  kolikkoa. Seuraavaksi tämän kolmion alle lisätään kolme uutta kolikkoa, joita on nyt yhteensä
kolikkoa. Seuraavaksi tämän kolmion alle lisätään kolme uutta kolikkoa, joita on nyt yhteensä  .
Etenemällä samaan tapaan huomataan, että esimerkiksi 10. kolmioluku saadaan laskemalla yhteen 10 ensimmäistä luonnollista lukua:
.
Etenemällä samaan tapaan huomataan, että esimerkiksi 10. kolmioluku saadaan laskemalla yhteen 10 ensimmäistä luonnollista lukua:
 Yleinen kaava kolmiolukujonon termeille on
Yleinen kaava kolmiolukujonon termeille on  . Kolmioluvuille käytetään yleensä merkintää
. Kolmioluvuille käytetään yleensä merkintää  (T = 'Triangle').
(T = 'Triangle').
Tämä motivoi seuraavaan määritelmään:
Määritelmä: Summajono
Olkoon  jono joukossa
jono joukossa  , jossa on määritelty yhteenlasku. Merkitään
, jossa on määritelty yhteenlasku. Merkitään
 Symboli
Symboli  on kreikkalainen kirjain sigma. Summausindeksi
on kreikkalainen kirjain sigma. Summausindeksi  kasvaa
alkuarvosta 1 loppuarvoon
kasvaa
alkuarvosta 1 loppuarvoon  .
.
Summajono saadaan siis alkuperäisestä jonosta laskemalla alkupään termejä yhteen aina yksi termi eteenpäin. Varsinkin sarjojen kohdalla käytetään nimeä osasummajono.
Kolmiolukujen yleinen kaava voidaan siis kirjoittaa muodossa
 ja kyseessä on luonnollisten lukujen jonon summajono.
ja kyseessä on luonnollisten lukujen jonon summajono.
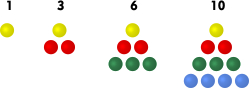
Esimerkki 3: Neliölukujen jono
Neliölukujen jono  määritellään kaavalla
määritellään kaavalla  . Tämän jonon termejä voidaan havainnollistaa asettelemalla kolikoita neliön muotoon.
. Tämän jonon termejä voidaan havainnollistaa asettelemalla kolikoita neliön muotoon.
Yksi mielenkiintoinen havainto on se, että kahden peräkkäisen kolmioluvun summa on aina neliöluku. Esimerkiksi  ja
ja  . Yleisesti määritelmiä käyttämällä
voidaan osoittaa, että
. Yleisesti määritelmiä käyttämällä
voidaan osoittaa, että

Esimerkki 4: Kuutiolukujen jono
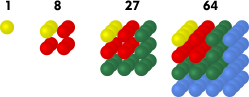
Määritelmä: Erotusjono (differenssijono)
Jonon  termeistä voidaan myös muodostaa peräkkäisten termien erotuksia:
termeistä voidaan myös muodostaa peräkkäisten termien erotuksia:
 on nimeltään alkuperäisen jonon
on nimeltään alkuperäisen jonon  ensimmäinen differenssijono.
ensimmäinen differenssijono.
Ensimmäisen differenssijonon ensimmäinen differenssijono on alkuperäisen jonon toinen differenssijono. sequence. Vastaavalla tavalla määritellään jonon  differenssijono.
differenssijono.
Esimerkki 6.
Eräitä tärkeitä jonoja
Eräät jonot ovat keskeisiä monille matemaattisille malleille ja niiden käytännön sovelluksille muilla aloilla kuten luonnontieteissä ja taloustieteissä.) Seuraavassa tarkastellaan kolme tällaista jonoa: aritmeettinen jono, geometrinen jono ja Fibonaccin lukujono.
Aritmeettinen jono
Aritmeettinen jono voidaan määritellä monella eri tavalla:Määritelmä A: Aritmeettinen jono
Jono  on aritmeettinen, jos sen peräkkäisten termien erotus
on aritmeettinen, jos sen peräkkäisten termien erotus  on vakio, t.s.
on vakio, t.s.

Huomautus: Aritmeettisen jonon eksplisiittinen kaava seuraa suoraan määritelmästä A:
 Aritmeettisen jonon
Aritmeettisen jonon  termi voidaan laskea myös palautuskaavan (eli rekursiokaavan) avulla:
termi voidaan laskea myös palautuskaavan (eli rekursiokaavan) avulla:

Määritelmä B: Aritmeettinen jono
Jono  on aritmeettinen jono, jos sen ensimmäinen differenssijono on vakiojono.
on aritmeettinen jono, jos sen ensimmäinen differenssijono on vakiojono.
Tämä määritelmä selventää myös aritmeettisen jonon nimen: Kolmen peräkkäisen termin keskimmäinen luku on kahden muun termin aritmeettinen keskiarvo; esimerkiksi
Geometrinen jono
Myös geometrisella jonolla on useita erilaisia määritelmiä:
Määritelmä: Geometrinen jono
Jono  on geometrinen, jos kahden präkkäisen termin suhde on aina vakio
on geometrinen, jos kahden präkkäisen termin suhde on aina vakio  , t.s.
, t.s.

Huomautus. Palautuskaava  geometrisen jonon termeille ja myös eksplisiittinen lauseke
geometrisen jonon termeille ja myös eksplisiittinen lauseke
 seuraavat suoraan määritelmästä.
seuraavat suoraan määritelmästä.
Myös tässä jonon nimityksellä on looginen tausta: Kolmen peräkkäisen termin keskimmäinen luku on aina kahden muun termin geometrinen keskiarvo; esimerkiksi

Esimerkki 2.
Olkoon  ja
ja  . Jono
. Jono  , jolle
, jolle  , eli
, eli
 on geometrinen jono. Jos
on geometrinen jono. Jos  ja
ja  , niin jono on aidosti
kasvava. Jos
, niin jono on aidosti
kasvava. Jos  ja
ja  , niin se on aidosti vähenevä. Jonon alkioiden muodostama joukko
, niin se on aidosti vähenevä. Jonon alkioiden muodostama joukko  on äärellinen, jos
on äärellinen, jos  (jolloin sen ainoa alkio on
(jolloin sen ainoa alkio on  ), muuten tämä joukko on ääretön.
), muuten tämä joukko on ääretön.
Fibonaccin jono
Fibonaccin lukujono on kuuluisa sen biologisten sovellusten vuoksi. Se esiintyy mm.eliöiden populaation kasvun yhteydessä ja kasvien rakenteessa. Palautuskaavaan perustuva määritelmä on seuraava:
Määritelmä: Fibonaccin jono
Olkoon  ja
ja
 kun
kun  . Jono
. Jono  on Fibonaccin lukujono. Jonon termit ovat Fibonaccin lukuja.
on Fibonaccin lukujono. Jonon termit ovat Fibonaccin lukuja.
Jonon nimen takana on italialainen Leonardo Pisano (1200-luvulla), latinalaiselta nimeltään Filius Bonacci. Hän tutki kaniparien lisääntymistä idealisoidussa tilanteessa, jossa kanit eivät kuole ja kaikki vanhat sekä uudet parit
lisääntyvät säännöllisin väliajoin. Näin hän päätyi jonoon

Esimerkki 3.
Auringonkukan kukat muodostuvat kahdesta spiraalista, jotka aukeavat keskeltä vastakkaisiin suuntiin: 55 spiraalia myötäpäivään ja 34 vastapäivään.
Myös ananashedelmän pinta käyttäytyy samalla tavalla. Siinä on 21 spiraalia yhteen suuntaan ja 34 vastakkaiseen. Myös joissakin kaktuksissa ja havupuiden kävyissä on samanlaisia rakenteita.

Suppeneminen, hajaantuminen ja raja-arvo
Tässä luvussa käsitellään jonon suppenemista. Aloitamme nollajonon käsitteestä ja siirrymme sen avulla yleiseen suppenemisen käsitteeseen.
Huomautus: Itseisarvo joukossa 
Itseisarvofunktio  on keskeisessä asemassa jonojen suppenemisen tutkimisessa. Seuraavassa käydään läpi sen tärkeimmät ominaisuudet:
on keskeisessä asemassa jonojen suppenemisen tutkimisessa. Seuraavassa käydään läpi sen tärkeimmät ominaisuudet:
Lause: Itseisarvon laskusääntöjä
Kohdat 1.-3. Results follow directly from the definition and by dividing it up into separate cases of the different signs of  and
and 
Kohta 4. Tämä kohta voidaan todistaa neliöön korottamalla tai tutkimalla kaikki eri vaihtoehdot kuten alla.
Tapaus 1.
Olkoot  . Silloin
. Silloin
 ja kaava pätee.
ja kaava pätee.
Tutkitaan lopuksi tapaus  and
and  , joka jakaantuu kahteen alakohtaan:
, joka jakaantuu kahteen alakohtaan:
Jos  ja
ja  , niin väite seuraa samalla periaatteella kuin tapauksessa 3, kun vaihdetaan keskenään
, niin väite seuraa samalla periaatteella kuin tapauksessa 3, kun vaihdetaan keskenään  ja
ja
 .
.
Nollajono
Esimerkki 1.
Jono  , joka on määritelty kaavalla
, joka on määritelty kaavalla  , eli
, eli  on nimeltään harmoninen jono. Jonon termit ovat positiivisia kaikilla
on nimeltään harmoninen jono. Jonon termit ovat positiivisia kaikilla  , mutta indeksin
, mutta indeksin  kasvaessa jonon termit pienenevät yhä lähemmäksi
nollaa.
kasvaessa jonon termit pienenevät yhä lähemmäksi
nollaa.
Jos esimerkiksi  , niin valinnalla
, niin valinnalla  pätee
pätee  aina, kun
aina, kun  .
.
Harmoninen jono suppenee kohti nollaa
Esimerkki 2.
Tarkastellaan jonoa  Olkoon
Olkoon  . Tällöin valinnalla
. Tällöin valinnalla  kaikille termeille
kaikille termeille  , joissa
, joissa  , pätee
, pätee  .
.
Note. Tutkittaessa nollajono-ominaisuutta täytyy tutkia mielivaltaista lukua  , jolle
, jolle  . Sen jälkeen
yritetään valita sellainen indeksi
. Sen jälkeen
yritetään valita sellainen indeksi  , josta alkaen jokainen
, josta alkaen jokainen  on pienempi kuin
on pienempi kuin  .
.
Esimerkki 3.
Kerrointen  vuoksi jonon kaksi peräkkäistä termiä ovat aina erimerkkisiä; tällaista jonoa kutsutaan yleisemmin vuorottelevaksi jonoksi.
vuoksi jonon kaksi peräkkäistä termiä ovat aina erimerkkisiä; tällaista jonoa kutsutaan yleisemmin vuorottelevaksi jonoksi.
Osoitetaan, että kyseessä on nollajono. Määritelmän mukaan jokaista  täytyy vastata sellainen
täytyy vastata sellainen  , että epäyhtälö
, että epäyhtälö
 pätee kaikille niille termeille
pätee kaikille niille termeille  , joissa
, joissa  .
.
Lause: Nollajonojen ominaisuuksia
Parts 1 and 2. If  is a zero sequence, then according to the definition there is an index
is a zero sequence, then according to the definition there is an index  , such that
, such that  for every
for every  and an arbitrary
and an arbitrary  . But then we have
. But then we have  ; this
proves parts 1 and 2 are correct.
; this
proves parts 1 and 2 are correct.
Part 3. If  , then the result is trivial. Let
, then the result is trivial. Let  and choose
and choose  such that
such that
 for all
for all  . Rearranging we get:
. Rearranging we get:

Part 4.
Because  is a zero sequence, by the definition we have
is a zero sequence, by the definition we have  for all
for all  . Analogously,
for the zero sequence
. Analogously,
for the zero sequence  there is a
there is a  with
with  for all
for all  .
.
Then for all  it follows (using the triangle inequality) that:
it follows (using the triangle inequality) that:

Suppeneminen ja hajaantuminen
Nollajonoja voidaan käyttää tutkimaan jonojen suppenemista yleisemmin:
Esimerkki 4.
Tarkastellaan jonoa  , jossa
, jossa
 Laskemalla jonon termejä suurilla
Laskemalla jonon termejä suurilla  , huomataan, että ilmeisesti
, huomataan, että ilmeisesti  , kun
, kun
 , joten jonon raja-arvo voisi olla
, joten jonon raja-arvo voisi olla  .
.
For a rigorous proof, we show that for every  there exists an index
there exists an index  , such that for every term
, such that for every term  with
with  the following relationship holds:
the following relationship holds:

Firstly we estimate the inequality:

Now, let  be an arbitrary constant. We then choose the index
be an arbitrary constant. We then choose the index  , such that
, such that
 Finally from the above inequality we have:
Finally from the above inequality we have:
 Thus we have proven the claim and so by definition
Thus we have proven the claim and so by definition  is
the limit of the sequence.
is
the limit of the sequence.
Jos jono suppenee, niin sillä voi olla vain yksi raja-arvo.
Lause: Raja-arvon yksikäsitteisyys
Oletetaan, että jono  suppenee kohti raja-arvoa
suppenee kohti raja-arvoa  ja kohti raja-arvoa
ja kohti raja-arvoa  .
Silloin
.
Silloin  .
.
Assume  ; choose
; choose  with
with  Then in particular
Then in particular ![[a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset. [a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset.](https://mycourses.aalto.fi/filter/tex/pix.php/4bac60723e473d9697be98685ce7659a.gif)
Because  converges to
converges to  , there is, according to the definition of convergence, a index
, there is, according to the definition of convergence, a index  with
with  for
for  Furthermore, because
Furthermore, because  converges to
converges to  there is also a
there is also a  with
with  for
for  For
For
 we have:
we have:
 Consequently we have obtained
Consequently we have obtained  , which is a contradiction as
, which is a contradiction as  .
Therefore the assumption must be wrong, so
.
Therefore the assumption must be wrong, so  .
.
Suppenevien jonojen ominaisuuksia
Lause: Laskusääntöjä
Olkoot  ja
ja  suppenevia jonoja, joille
suppenevia jonoja, joille  ja
ja  .
Silloin kaikille
.
Silloin kaikille  pätee:
pätee:
Sanallisesti: Suppenevien jonojen summat ja tulot ovat suppenevia jonoja.
Part 1. Let  . We must show, that for all
. We must show, that for all  it follows that:
it follows that:
 The left hand side we estimate using:
The left hand side we estimate using:

Because  and
and  converge, for each given
converge, for each given  it holds true that:
it holds true that:

Therefore
 for all numbers
for all numbers  . Therefore the sequence
. Therefore the sequence
 is a zero sequence and the desired inequality is shown.
is a zero sequence and the desired inequality is shown.
Part 2. Let  . We have to show, that for all
. We have to show, that for all 
 Furthermore an estimation of the left hand side follows:
Furthermore an estimation of the left hand side follows:
 We choose a number
We choose a number  , such that
, such that  for all
for all  and
and  . Such a value of
. Such a value of  exists by the Theorem of convergent sequences being bounded. We can then use the estimation:
exists by the Theorem of convergent sequences being bounded. We can then use the estimation:
 For all
For all  we have
we have
 and
and  , and - putting everything together - the desired inequality it shown.
, and - putting everything together - the desired inequality it shown.
 ';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
/* fibonacci sequence */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox: [-1, 40, 10, -5],
axis: false,
shownavigation: false,
showcopyright: false
});
var xaxis = board.create('axis', [
[0, 0],
[1, 0]
], {
straightFirst: false,
highlight: false,
drawZero: true,
ticks: {
drawLabels: false,
minorTicks: 0,
majorHeight: 15,
label: {
highlight: false,
offset: [0, -15]
}
}
});
var yaxis = board.create('axis', [
[0, 0],
[0, 1]
], {
straightFirst: false,
highlight: false,
ticks: {
minorTicks: 0,
majorHeight: 15,
label: {
offset: [-15, 0],
position: 'lrt',
highlight: false
}
}
});
xaxis.defaultTicks.ticksFunction = function() {
return 1;
};
yaxis.defaultTicks.ticksFunction = function() {
return 5;
};
var a_k = [1, 1];
var newbar = function(k) {
var y;
if (k - 1 > a_k.length - 1) {
y = a_k[k - 3] + a_k[k - 2];
a_k.push(y);
} else {
y = a_k[k - 1];
}
return board.create('polygon', [
[k - 1 / 4, 0],
[k + 1 / 4, 0],
[k + 1 / 4, y],
[k - 1 / 4, y]
], {
vertices: {
visible: false
},
borders: {
strokeColor: 'black',
strokeOpacity: .6,
highlight: false
},
fillColor: '#b2caeb',
fixed: true,
highlight: false
});
}
var bars = [];
for (var i = 0; i < 9; i++) {
const k = i + 1;
board.create('text', [k - .1, -.6, function() {
return '
';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
/* fibonacci sequence */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox: [-1, 40, 10, -5],
axis: false,
shownavigation: false,
showcopyright: false
});
var xaxis = board.create('axis', [
[0, 0],
[1, 0]
], {
straightFirst: false,
highlight: false,
drawZero: true,
ticks: {
drawLabels: false,
minorTicks: 0,
majorHeight: 15,
label: {
highlight: false,
offset: [0, -15]
}
}
});
var yaxis = board.create('axis', [
[0, 0],
[0, 1]
], {
straightFirst: false,
highlight: false,
ticks: {
minorTicks: 0,
majorHeight: 15,
label: {
offset: [-15, 0],
position: 'lrt',
highlight: false
}
}
});
xaxis.defaultTicks.ticksFunction = function() {
return 1;
};
yaxis.defaultTicks.ticksFunction = function() {
return 5;
};
var a_k = [1, 1];
var newbar = function(k) {
var y;
if (k - 1 > a_k.length - 1) {
y = a_k[k - 3] + a_k[k - 2];
a_k.push(y);
} else {
y = a_k[k - 1];
}
return board.create('polygon', [
[k - 1 / 4, 0],
[k + 1 / 4, 0],
[k + 1 / 4, y],
[k - 1 / 4, y]
], {
vertices: {
visible: false
},
borders: {
strokeColor: 'black',
strokeOpacity: .6,
highlight: false
},
fillColor: '#b2caeb',
fixed: true,
highlight: false
});
}
var bars = [];
for (var i = 0; i < 9; i++) {
const k = i + 1;
board.create('text', [k - .1, -.6, function() {
return ' ';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
';
}], {
useMathJax: true,
strokeColor: '#2183de',
fontSize: 13,
fixed: true,
highlight: false
});
board.fullUpdate();
})();
';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
board.create('point', [i, 1 / i], {
size: 4,
name: '',
strokeWidth: .5,
strokeColor: 'black',
face: 'diamond',
fillColor: '#cf4490',
fixed: true
});
}
board.fullUpdate();
})();
';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
';
}], {
useMathJax: true,
strokeColor: '#2183de',
fontSize: 13,
fixed: true,
highlight: false
});
board.fullUpdate();
})();
';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
board.create('point', [i, 1 / i], {
size: 4,
name: '',
strokeWidth: .5,
strokeColor: 'black',
face: 'diamond',
fillColor: '#cf4490',
fixed: true
});
}
board.fullUpdate();
})();
2. Sarjat
Suppeneminen
Suppeneminen
Jonosta  voidaan muodostaa sen osasummia asettamalla
voidaan muodostaa sen osasummia asettamalla 
Jos osasumminen jonolla  on raja-arvo
on raja-arvo  , niin luvuista
, niin luvuista  muodostettu sarja suppenee ja sen summa on
muodostettu sarja suppenee ja sen summa on  . Tällöin merkitään
. Tällöin merkitään

Sarjan hajaantuminen
Sarja, joka ei suppene, on hajaantuva. Tämä voi tapahtua kolmella eri tavalla:
- sarjan osasummat kasvavat rajatta kohti ääretöntä
- sarjan osasummat pienenevät rajatta kohti miinus ääretöntä
- osasummien jono heilahtelee niin, ettei sillä ole raja-arvoa.
Hajaantuvan sarjan kohdalla merkintä  ei oikeastaan tarkoita mitään (se ei ole reaaliluku). Tällöin voidaan tulkita, että merkintä tarkoittaa osasummien jonoa, joka on aina hyvin määritelty.
ei oikeastaan tarkoita mitään (se ei ole reaaliluku). Tällöin voidaan tulkita, että merkintä tarkoittaa osasummien jonoa, joka on aina hyvin määritelty.
Perustuloksia
Geometrinen sarja
Geometrinen sarja
 suppenee, jos
suppenee, jos  (tai
(tai  ), jolloin sen summa on
), jolloin sen summa on  . Jos
. Jos  , niin sarja hajaantuu.
, niin sarja hajaantuu.
Laskusääntöjä
Suppenevien sarjojen ominaisuuksia:
Todistus. Nämä seuraavat vastaavista tuloksista jonojen raja-arvolle.

Huomautus: Sarjoilla ei ole jonojen kaltaista tulosääntöä, koska jo kahden termin summille
 Tulosäännön oikea muoto on sarjojen Cauchy-tulo, jossa myös ristitermit otetaan huomioon.
Tulosäännön oikea muoto on sarjojen Cauchy-tulo, jossa myös ristitermit otetaan huomioon.
Katso esimerkiksi https://en.wikipedia.org/wiki/Cauchy_product
Huomautus: Ominaisuutta  ei voi käyttää sarjan suppenemisen osoittamiseen; vrt. seuraavat esimerkit.
Tämä on eräs yleisimmistä päättelyvirheistä sarjojen kohdalla!
ei voi käyttää sarjan suppenemisen osoittamiseen; vrt. seuraavat esimerkit.
Tämä on eräs yleisimmistä päättelyvirheistä sarjojen kohdalla!
Esimerkki
Ratkaisu. Sarjan yleisen termin raja-arvo on
 Koska raja-arvo ei ole nolla, niin sarja hajaantuu.
Koska raja-arvo ei ole nolla, niin sarja hajaantuu.
Tämän klassisen tuloksen todisti ensimmäisenä 14. vuosisadalla Nicole Oresme, jonka jälkeen monia muitakin perusteluja on keksitty. Tässä esimerkkinä kaksi erilaista päättelyä.
i) Alkeellinen todistus. Oletetaan, että sarja suppenee ja yritetään johtaa tästä ristiriita. Olkoon siis  harmonisen sarjan summa:
harmonisen sarjan summa:  . Tällöin
. Tällöin
 Selvästi
Selvästi
 joten
joten 
 Päädyimme siis epäyhtälöön
Päädyimme siis epäyhtälöön  , joka on ristiriita. Alkuperäinen oletus suppenemisesta on siis väärä, joten sarja hajaantuu.
, joka on ristiriita. Alkuperäinen oletus suppenemisesta on siis väärä, joten sarja hajaantuu.
ii) Todistus integraalin avulla: Pylvään korkeuksia  vastaavan histogrammin alapuolelle jää funktion
vastaavan histogrammin alapuolelle jää funktion  kuvaaja, joten pinta-aloja vertaamalla saadaan
kuvaaja, joten pinta-aloja vertaamalla saadaan
 kun
kun  .
.

Positiiviset sarjat
Sarjan summan laskeminen on usein vaikeata ja monesti jopa mahdotonta, jos vaatimuksena on summan eksplisiittinen lauseke. Moniin sovelluksiin riittää myös summan likiarvo, mutta sitä ennen olisi syytä selvittää, onko sarja suppeneva vai hajaantuva.
Sarja  on positiivinen (tai positiiviterminen), jos
on positiivinen (tai positiiviterminen), jos  kaikilla
kaikilla  .
.
Positiivisten sarjojen suppeneminen on hyvin selväpiirteistä:
Lause 2.
Positiivinen sarja suppenee täsmälleen silloin, kun sen osasummien jono on ylhäältä rajoitettu.
Syy: Osasummien jono on nouseva.
Esimerkki
Osoita, että superharmonisen sarjan
 osasummille pätee
osasummille pätee  kaikilla
kaikilla  , joten sarja suppenee.
, joten sarja suppenee.
Ratkaisu. Ratkaisu perustuu epäyhtälöön
 kun
kun  , koska sen mukaan
, koska sen mukaan
 kaikilla
kaikilla  .
.
Tämän päättelyn voi tehdä myös integraalin avulla.
Leonhard Euler selvitti vuonna 1735, että sarjan summa on  . Perusteluna hän käytti sinifunktion sarja- ja tulokehitelmien vertailua.
. Perusteluna hän käytti sinifunktion sarja- ja tulokehitelmien vertailua.
Itseinen suppeneminen
Lause 3.
Itseisesti suppeneva sarja suppenee (tavallisessa mielessä) ja

Tämä on erikoistapaus majoranttiperiaatteesta, josta lisää myöhemmin.
Oletetaan, että  suppenee. Tarkastellaan erikseen sarjan
suppenee. Tarkastellaan erikseen sarjan  positiivista ja negatiivista osaa: Olkoon
positiivista ja negatiivista osaa: Olkoon  Koska
Koska  , niin positiiviset sarjat
, niin positiiviset sarjat  ja
ja  suppenevat lauseen 2 perusteella. Lisäksi
suppenevat lauseen 2 perusteella. Lisäksi  , joten
, joten  suppenee kahden suppenevan sarjan erotuksena.
suppenee kahden suppenevan sarjan erotuksena.

Esimerkki
Tutki vuorottelevan (= etumerkit vaihtelevat vuorotellen + ja -) sarjan  suppenemista.
suppenemista.
Ratkaisu. Koska
 ja superharmoninen sarja
ja superharmoninen sarja
 suppenee, niin tutkittava sarja suppenee itseisesti, ja sen vuoksi myös tavallisessa mielessä.
suppenee, niin tutkittava sarja suppenee itseisesti, ja sen vuoksi myös tavallisessa mielessä.
Vuorotteleva harmoninen sarja
Itseinen suppeneminen ei kuitenkaan tarkoita samaa kuin tavallinen suppeneminen:
Esimerkki
Vuorotteleva harmoninen sarja
 suppenee, mutta ei itseisesti.
suppenee, mutta ei itseisesti.
(Idea) Piirretään osasummajonon  kuvaaja, josta huomataan, että parillisten ja parittomien indeksien osasummat
kuvaaja, josta huomataan, että parillisten ja parittomien indeksien osasummat  ja
ja  ovat monotonisia ja suppenevat kohti samaa raja-arvoa.
ovat monotonisia ja suppenevat kohti samaa raja-arvoa.
Sarjan summa on  , joka saadaan selville integroimalla geometrisen sarjan summakaavaa.
, joka saadaan selville integroimalla geometrisen sarjan summakaavaa.
pisteet on yhdistetty janoilla havainnollisuuden vuoksi
Suppenemistestejä
Vertailutestit
Edelliset tarkastelut yleistyvät seuraavalla tavalla:
Esimerkki
Ratkaisu. Koska kaikilla
kaikilla  , niin ensimmäinen sarja suppenee majoranttiperiaatteen nojalla.
, niin ensimmäinen sarja suppenee majoranttiperiaatteen nojalla.
Toisaalta  kaikilla
kaikilla  , joten toisella sarjalla on hajaantuva harmoninen minorantti, joten se hajaantuu.
, joten toisella sarjalla on hajaantuva harmoninen minorantti, joten se hajaantuu.
Suhdetesti
Käytännössä eräs parhaista tavoista tutkia suppenemista on suhdetesti, jossa sarjan peräkkäisten termien käyttäytymistä verrataan sopivaan geometriseen sarjaan:
Suhdetestin raja-arvomuoto
(Idea) Geometriselle sarjalle kahden peräkkäisen termin suhde on täsmälleen  . Suhdetestin mukaan muidenkin sarjojen suppenemista voidaan (usein) tutkia samalla periaatteella, kun
suhdeluku
. Suhdetestin mukaan muidenkin sarjojen suppenemista voidaan (usein) tutkia samalla periaatteella, kun
suhdeluku  korvataan tällä raja-arvolla.
korvataan tällä raja-arvolla.
Valitaan raja-arvon määritelmässä  . Silloin jostakin indeksistä
. Silloin jostakin indeksistä  alkaen pätee
alkaen pätee
 ja väite seuraa lauseesta 4.
ja väite seuraa lauseesta 4.
Tapauksessa  sarjan yleinen termi ei lähesty nollaa, joten sarja hajaantuu.
sarjan yleinen termi ei lähesty nollaa, joten sarja hajaantuu.
Viimeinen tapaus  ei sisällä mitään informaatiota (eikä myöskään todistettavaa).
ei sisällä mitään informaatiota (eikä myöskään todistettavaa).
Tämä tapaus esiintyy sekä harmonisen ( , hajaantuu!) että yliharmonisen (
, hajaantuu!) että yliharmonisen ( , suppenee!) sarjan kohdalla. Näissä tapauksissa suppenemista täytyy tutkia joillakin muilla menetelmillä, kuten aikaisemmin tehtiin.
, suppenee!) sarjan kohdalla. Näissä tapauksissa suppenemista täytyy tutkia joillakin muilla menetelmillä, kuten aikaisemmin tehtiin.

3. Jatkuvuus
Sisältö
- Funktion raja-arvo
- Raja-arvo ja jatkuvuus
- Jatkuvien funktioiden ominaisuuksia
Tässä luvussa määritellään funktion  raja-arvo pisteessä
raja-arvo pisteessä  . Oletamme, että lukija tuntee ennestään reaalimuuttujan funktion käsitteen ja lukujonon raja-arvon.
. Oletamme, että lukija tuntee ennestään reaalimuuttujan funktion käsitteen ja lukujonon raja-arvon.
Funktion raja-arvo
Olkoon  reaalilukujen osajoukko ja
reaalilukujen osajoukko ja  sellainen piste, että on olemassa jono pisteitä
sellainen piste, että on olemassa jono pisteitä  , joille
, joille  , kun
, kun  . Usein
. Usein  on kaikkien reaalilukujen joukko, mutta toisinaan myös väli (avoin, puoliavoin tai suljettu).
on kaikkien reaalilukujen joukko, mutta toisinaan myös väli (avoin, puoliavoin tai suljettu).
Esimerkki 1.
Pisteen  ei tarvitse kuulua joukkoon
ei tarvitse kuulua joukkoon  . Esimerkiksi jono
. Esimerkiksi jono  joukossa
joukossa ![S=\, ]0,2[ S=\, ]0,2[](https://mycourses.aalto.fi/filter/tex/pix.php/5a611f94acc4b7abf3b85346aedbe506.gif) , kun
, kun  , ja
, ja  kaikilla
kaikilla  , mutta
, mutta  ei kuulu joukkoon
ei kuulu joukkoon  .
.
Toispuoleiset raja-arvot
Raja-arvon tärkeä ominaisuus on sen yksikäsitteisyys. Tämä tarkoittaa sitä, että tapauksessa  ja
ja  täytyy olla
täytyy olla  . Tästä huolimatta voi usein olla hyödyllistä tutkia funktion käyttäytymistä, kun
. Tästä huolimatta voi usein olla hyödyllistä tutkia funktion käyttäytymistä, kun  lähestyy tutkittavaa pistettä
lähestyy tutkittavaa pistettä  vain vasemmalta tai oikealta. Näitä kutsutaan funktion
vain vasemmalta tai oikealta. Näitä kutsutaan funktion  vasemman- tai oikeanpuoleisiksi raja-arvoiksi pisteessä
vasemman- tai oikeanpuoleisiksi raja-arvoiksi pisteessä  .
.
Määritelmä 2: Toispuoleiset raja-arvot
Olkoon  ja
ja  funktio, joka on määritelty (ainakin) joukossa
funktio, joka on määritelty (ainakin) joukossa  . Tällöin funktiolla
. Tällöin funktiolla  has a vasemmanpuoleinen raja-arvo
has a vasemmanpuoleinen raja-arvo  pisteessä
pisteessä  , merkitään
, merkitään
 jos
jos  , kun
, kun  kaikille niille jonoille
kaikille niille jonoille  joukossa
joukossa
![S\cap ]-\infty,x_0[ =\{ x\in S : x < x_0 \} S\cap ]-\infty,x_0[ =\{ x\in S : x < x_0 \}](https://mycourses.aalto.fi/filter/tex/pix.php/c65f5d0e098970db4a09f85ad08fada6.gif) , joille
, joille  , kun
, kun  .
.
Vastaavasti funktiolla  on oikeanpuoleinen raja-arvo
on oikeanpuoleinen raja-arvo  pisteessä
pisteessä  , merkitään
, merkitään
 , jos
, jos  , kun
, kun  kaikille niille jonoille
kaikille niille jonoille  joukossa
joukossa ![S\cap ]x_0,\infty[ =\{ x\in S : x_0 < x \} S\cap ]x_0,\infty[ =\{ x\in S : x_0 < x \}](https://mycourses.aalto.fi/filter/tex/pix.php/34e4590988ffbbcc84fe6f2077270c14.gif) , joille
, joille  , kun
, kun  .
.
Esimerkki 6.
Laskusääntöjä
Raja-arvojen laskusäännöt seuraavat suoraan vastaavista lukujonojen raja-arvon ominaisuuksista.
Raja-arvot ja jatkuvuus
Tässä kappaleessa määritellään funktion jatkuvuus. Jatkuvuuden intuitiivinen tulkinta on se, että funktion kuvaaja on yhtenäinen viiva. Tämä ei kuitenkaan ole matemaattisesti riittävän tarkka määritelmä, koska se mm. sisältää epämääräisiä (?) käsitteitä kuten "yhtenäinen" ja "viiva". Tämän perusteella voi esimerkiksi olla vaikea päättää, onko funktio  jatkuva vai ei.
jatkuva vai ei.
Esimerkki 1.
Esimerkki 2.
Olkoon  . Määritellään funktio
. Määritellään funktio  asettamalla
asettamalla
 Silloin
Silloin
 Tämän vuoksi
Tämän vuoksi  ei ole jatkuva pisteessä
ei ole jatkuva pisteessä  .
.
Seuraavaksi esitellään joitakin jatkuvien funktioiden perusominaisuuksia. Raja-arvosääntöjen avulla (Lause 2) saadaan:
Lause 3.
Jatkuvien funktioiden summa ja tulo ovat jatkuvia. Erityisesti polynomit ovat jatkuvia funktioita. Jos  ja
ja  ovat jatkuvia ja
ovat jatkuvia ja  , niin
, niin  on jatkuva pisteessä
on jatkuva pisteessä  .
.
Jatkuvien funktioiden yhdistetty funktio on jatkuva, kunhan se on määritelty:
Lause 4.
Olkoot  ja
ja  . Oletetaan, että
. Oletetaan, että  on jatkuva pisteessä
on jatkuva pisteessä  ja
ja  on jatkuva pisteessä
on jatkuva pisteessä  . Tällöin
. Tällöin  on jatkuva pisteessä
on jatkuva pisteessä  .
.
Huom. Jos  on jatkuva, niin
on jatkuva, niin  on jatkuva.
on jatkuva.
Miksi?
Huom. Jos  and
and  ovat jatkuvia, niin
ovat jatkuvia, niin  ja
ja  ovat jatkuvia. (Tässä
ovat jatkuvia. (Tässä  .)
.)
Miksi?
 '}], {
strokeColor : colors[1],
fontSize : 16,
visible : false
});
l[2] = board.create('text', [-4, 3, function() { return '
'}], {
strokeColor : colors[1],
fontSize : 16,
visible : false
});
l[2] = board.create('text', [-4, 3, function() { return ' '}], {
strokeColor : colors[2],
fontSize : 16,
visible : false
});
g[0] = board.create('functiongraph', [f0, -6, 6], {
visible : true,
strokeWidth : 1.5,
strokeColor : colors[0],
highlight : false
});
g[1] = board.create('functiongraph', [f1, -6, 6], {
visible : false,
strokeWidth : 1.5,
strokeColor : colors[1],
highlight : false
});
g[2] = board.create('functiongraph', [f2, -6, 6], {
visible : false,
strokeWidth : 1.5,
strokeColor : colors[2],
highlight : false
});
var currentGraph = g[0];
var currentLabel = l[0];
select.on('drag', function() {
currentGraph.setAttribute({ visible : false });
currentLabel.setAttribute({ visible : false });
currentGraph = g[select.Value()];
currentLabel = l[select.Value()];
currentGraph.setAttribute({ visible : true });
currentLabel.setAttribute({ visible : true, useMathJax : true });
select.setAttribute({ fillColor : colors[select.Value()] });
board.update();
});
board.fullUpdate();
})();
/* Example 2. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox16', {
boundingbox : [-3.5, 4.5, 3.5, -1.25],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]]);
xaxis.removeAllTicks();
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
drawZero : true,
ticks : { majorHeight : 5, minorTicks : 0, ticksDistance : 1.0 }
});
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var xtick = board.create('segment', [[1, .05],[1, -.1]], {
strokeWidth : 1, strokeColor : 'black', strokeOpacity : .4,
highlight : false });
var f = function(x) { return 2; }
var g = function(x) { return 3; }
board.create('functiongraph', [f, -3.5, 1], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [g, 1, 3.5], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.create('point', [1, f(1)], {
name : '',
fillColor : 'white',
strokeColor : 'black',
strokeWidth : .5,
size : 2,
fixed : true,
showInfobox : false
});
board.create('point', [1, g(1)], {
name : '',
fillColor : 'black',
strokeColor : 'black',
strokeWidth : .5,
size : 2,
fixed : true,
showInfobox : false
});
var x0 = board.create('text', [1, 0, function() { return '
'}], {
strokeColor : colors[2],
fontSize : 16,
visible : false
});
g[0] = board.create('functiongraph', [f0, -6, 6], {
visible : true,
strokeWidth : 1.5,
strokeColor : colors[0],
highlight : false
});
g[1] = board.create('functiongraph', [f1, -6, 6], {
visible : false,
strokeWidth : 1.5,
strokeColor : colors[1],
highlight : false
});
g[2] = board.create('functiongraph', [f2, -6, 6], {
visible : false,
strokeWidth : 1.5,
strokeColor : colors[2],
highlight : false
});
var currentGraph = g[0];
var currentLabel = l[0];
select.on('drag', function() {
currentGraph.setAttribute({ visible : false });
currentLabel.setAttribute({ visible : false });
currentGraph = g[select.Value()];
currentLabel = l[select.Value()];
currentGraph.setAttribute({ visible : true });
currentLabel.setAttribute({ visible : true, useMathJax : true });
select.setAttribute({ fillColor : colors[select.Value()] });
board.update();
});
board.fullUpdate();
})();
/* Example 2. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox16', {
boundingbox : [-3.5, 4.5, 3.5, -1.25],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]]);
xaxis.removeAllTicks();
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
drawZero : true,
ticks : { majorHeight : 5, minorTicks : 0, ticksDistance : 1.0 }
});
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var xtick = board.create('segment', [[1, .05],[1, -.1]], {
strokeWidth : 1, strokeColor : 'black', strokeOpacity : .4,
highlight : false });
var f = function(x) { return 2; }
var g = function(x) { return 3; }
board.create('functiongraph', [f, -3.5, 1], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [g, 1, 3.5], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.create('point', [1, f(1)], {
name : '',
fillColor : 'white',
strokeColor : 'black',
strokeWidth : .5,
size : 2,
fixed : true,
showInfobox : false
});
board.create('point', [1, g(1)], {
name : '',
fillColor : 'black',
strokeColor : 'black',
strokeWidth : .5,
size : 2,
fixed : true,
showInfobox : false
});
var x0 = board.create('text', [1, 0, function() { return ' '; }], {
useMathJax : true
});
board.fullUpdate();
})();
'; }], {
useMathJax : true
});
board.fullUpdate();
})();
Epsilon-delta määritelmä
Seuraavaksi esitetään jatkuvuuden  -määritelmä. Tärkein idea on se, että jos
-määritelmä. Tärkein idea on se, että jos  on jatkuva pisteessä
on jatkuva pisteessä  , niin funktion arvojen
, niin funktion arvojen  pitäisi lähestyä arvoa
pitäisi lähestyä arvoa  , kun
, kun  lähestyy pistettä
lähestyy pistettä  .
.
Tämä määritelmä yleistyy muillekin kuin tällä kurssilla käsitellyille reaalifunktioille.
Esimerkki 3.
 ', fillColor : '#bd4444', snapWidth : 0.01,
label : { useMathJax : true, strokeColor : '#bd4444', offset : [0, 25] }});
var x1 = board.create('glider', [1/2, 0, xaxis],
{ name: '
', fillColor : '#bd4444', snapWidth : 0.01,
label : { useMathJax : true, strokeColor : '#bd4444', offset : [0, 25] }});
var x1 = board.create('glider', [1/2, 0, xaxis],
{ name: ' ', strokeColor : 'black', strokeWidth : .5, fillColor : '#446abd', showinfobox : false,
label : { useMathJax : true, strokeColor : '#446abd', offset : [5, 25] } });
/*board.suspendUpdate();*/
var y1 = board.create('point', [0, function(){return f(x1.X());}],
{ name : '
', strokeColor : 'black', strokeWidth : .5, fillColor : '#446abd', showinfobox : false,
label : { useMathJax : true, strokeColor : '#446abd', offset : [5, 25] } });
/*board.suspendUpdate();*/
var y1 = board.create('point', [0, function(){return f(x1.X());}],
{ name : ' ', size : 2, strokeColor : 'black', strokeWidth : .5, fillColor : '#bd4444',
showinfobox : false, highlight : false,
label : { useMathJax : true, strokeColor : '#bd4444', offset : [5, 25] }});
var y2 = board.create('point', [0, function(){return f(x1.X())-s.Value();}], { visible : false });
var y3 = board.create('point', [0, function(){return f(x1.X())+s.Value();}], { visible : false });
var z1 = board.create('point', [function(){return y1.Y()/4;}, function(){return y1.Y();}], { visible : false });
var z2 = board.create('point', [function(){return y2.Y()/4;}, function(){return y2.Y();}], { visible : false });
var z3 = board.create('point', [function(){return y3.Y()/4;}, function(){return y3.Y();}], { visible : false });
var v1 = board.create('segment', [z1, y1], { strokeColor : '#bd4444', strokeWidth : 1, highlight : false });
var v2 = board.create('line', [z2, y2], { strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var v3 = board.create('line', [z3, y3], { strokeColor: '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var epsilon = board.create('polygon', [function() { return [-.5, y2.Y()]; }, function() { return [2.5, y2.Y()]; },
function() { return [2.5, y3.Y()]; }, function() { return [-.5, y3.Y()]; }],
{ fillColor : '#bd4444', fillOpacity : .3, highlight : false, vertices : { visible : false }, borders : { visible : false }});
var h1 = board.create('segment', [function() { return x1; }, function() { return z1; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var h2 = board.create('segment', [function() { return [z2.X(), 0]; },
function() { return [z2.X(), 8]}], { strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var h3 = board.create('segment', [function() { return [z3.X(), 0]; },
function() { return [z3.X(), 8]}], { strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var delta = board.create('polygon', [h2.point1, h2.point2, h3.point2, h3.point1],
{ fillColor : '#446abd', fillOpacity : .3, highlight : false, vertices : { visible : false }, borders : { visible : false }});
var txt = board.create('text', [-2.5, .7, function() {
return '
', size : 2, strokeColor : 'black', strokeWidth : .5, fillColor : '#bd4444',
showinfobox : false, highlight : false,
label : { useMathJax : true, strokeColor : '#bd4444', offset : [5, 25] }});
var y2 = board.create('point', [0, function(){return f(x1.X())-s.Value();}], { visible : false });
var y3 = board.create('point', [0, function(){return f(x1.X())+s.Value();}], { visible : false });
var z1 = board.create('point', [function(){return y1.Y()/4;}, function(){return y1.Y();}], { visible : false });
var z2 = board.create('point', [function(){return y2.Y()/4;}, function(){return y2.Y();}], { visible : false });
var z3 = board.create('point', [function(){return y3.Y()/4;}, function(){return y3.Y();}], { visible : false });
var v1 = board.create('segment', [z1, y1], { strokeColor : '#bd4444', strokeWidth : 1, highlight : false });
var v2 = board.create('line', [z2, y2], { strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var v3 = board.create('line', [z3, y3], { strokeColor: '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var epsilon = board.create('polygon', [function() { return [-.5, y2.Y()]; }, function() { return [2.5, y2.Y()]; },
function() { return [2.5, y3.Y()]; }, function() { return [-.5, y3.Y()]; }],
{ fillColor : '#bd4444', fillOpacity : .3, highlight : false, vertices : { visible : false }, borders : { visible : false }});
var h1 = board.create('segment', [function() { return x1; }, function() { return z1; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var h2 = board.create('segment', [function() { return [z2.X(), 0]; },
function() { return [z2.X(), 8]}], { strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var h3 = board.create('segment', [function() { return [z3.X(), 0]; },
function() { return [z3.X(), 8]}], { strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var delta = board.create('polygon', [h2.point1, h2.point2, h3.point2, h3.point1],
{ fillColor : '#446abd', fillOpacity : .3, highlight : false, vertices : { visible : false }, borders : { visible : false }});
var txt = board.create('text', [-2.5, .7, function() {
return ' '; }], {
strokeColor : '#446abd', useMathJax : true, fixed : true
});
/*board.unsuspendUpdate();*/
board.fullUpdate();
})();
'; }], {
strokeColor : '#446abd', useMathJax : true, fixed : true
});
/*board.unsuspendUpdate();*/
board.fullUpdate();
})();
Esimerkki 4.
Olkoon  . Määritellään funktio
. Määritellään funktio  asettamalla
asettamalla
 Esimerkissä 2 nähtiin, että tämä funktio on epäjatkuva pisteessä
Esimerkissä 2 nähtiin, että tämä funktio on epäjatkuva pisteessä  . Tämän todistamiseksi
. Tämän todistamiseksi  -määritelmää käyttämällä täytyy löytää sellainen
-määritelmää käyttämällä täytyy löytää sellainen  ja
ja  , että kaikilla
, että kaikilla  on voimassa
on voimassa  , mutta
, mutta  .
.
Todistus. Olkoon  ja
ja  . Valitsemalla
. Valitsemalla  on voimassa
on voimassa
 ja
ja
 Näin ollen Lauseen 5 perusteella
Näin ollen Lauseen 5 perusteella  ei ole jatkuva pisteessä
ei ole jatkuva pisteessä  .
.

 ', strokeWidth : .3, strokeColor : 'black', fillColor : '#446abd', showinfobox : false,
highlight : false, fixed : true,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#446abd' }});
board.suspendUpdate();
var x2 = board.create('point', [ function(){return x1.X()-s.Value();}, 0],
{ visible : false });
var x3 = board.create('point', [function(){return x1.X()+s.Value();},0],
{ visible : false });
var y1 = board.create('point', [-2, function() { return f(x1.X()); }],
{ size : 2, name: '
', strokeWidth : .3, strokeColor : 'black', fillColor : '#446abd', showinfobox : false,
highlight : false, fixed : true,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#446abd' }});
board.suspendUpdate();
var x2 = board.create('point', [ function(){return x1.X()-s.Value();}, 0],
{ visible : false });
var x3 = board.create('point', [function(){return x1.X()+s.Value();},0],
{ visible : false });
var y1 = board.create('point', [-2, function() { return f(x1.X()); }],
{ size : 2, name: ' ', strokeWidth : .3, strokeColor : 'black', fillColor : '#446abd', showinfobox : false,
highlight : false,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#446abd' } });
var yd = board.create('point', [-2, function() { return f(x2.X()); }], {
size : 2, name: '
', strokeWidth : .3, strokeColor : 'black', fillColor : '#446abd', showinfobox : false,
highlight : false,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#446abd' } });
var yd = board.create('point', [-2, function() { return f(x2.X()); }], {
size : 2, name: ' ', strokeWidth : .3, strokeColor : 'black', fillColor : '#bd4444', showinfobox : false,
highlight : false,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#bd4444' }
});
/* doesn't really do anything atm... */
var dist = function() { if (Math.abs(f(x1)-f(x2.X())) != 0 || Math.abs(f(x1)-f(x3.X())) != 0) { return .5; } else { return 0; } };
var y2 = board.create('point', [0, function() {
return y1.Y()-dist(); }],
{ visible : false });
var y3 = board.create('point', [0, function() {
return y1.Y()+dist(); }],
{ visible : false });
var endpoint1 = board.create('point', [0, 2],
{ name : '', fixed : true, size : 2, fillColor : 'white', strokeWidth : .5, strokeColor : 'black', showinfobox : false });
var endpoint2 = board.create('point', [0, 3],
{ name : '', fixed : true, size : 2, fillColor : 'black', strokeWidth : .5, strokeColor : 'black', showinfobox : false });
var v1 = board.create('segment', [x1, function() { return [x1.X(), y1.Y()]; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var v2 = board.create('line', [x2, function() { return [x2.X(), x2.Y()+1]; }],
{ strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var v3 = board.create('line', [x3, function() { return [x3.X(), x3.Y()+1]; }],
{ strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var delta = board.create('polygon', [function() { return [x2.X(), -5]; }, function() { return [x2.X(), 6]; },
function() { return [x3.X(), 6]; }, function() { return [x3.X(), -5]; }], {
highlight : false, fixed : true, vertices : { visible : false }, borders : { visible : false }, fillColor : '#446abd',
fillOpacity : .2
});
var h1 = board.create('segment', [y1, function() { return [x1.X(), y1.Y()]; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var h2 = board.create('line', [function() { return y2; }, function() { return [y2.X()+1, y2.Y()]; }],
{ strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var h3 = board.create('line', [function() { return y3; }, function() { return [y3.X()+1, y3.Y()]; }],
{ strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var epsilon = board.create('polygon', [[-5, 3.5],[10, 3.5],[10, 2.5], [-5, 2.5]], {
highlight : false, fixed : true, vertices : { visible : false }, borders : { visible : false }, fillColor : '#bd4444',
fillOpacity : .2
});
var txt = board.create('text', [4.2, -1.5, function() {
return '
', strokeWidth : .3, strokeColor : 'black', fillColor : '#bd4444', showinfobox : false,
highlight : false,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#bd4444' }
});
/* doesn't really do anything atm... */
var dist = function() { if (Math.abs(f(x1)-f(x2.X())) != 0 || Math.abs(f(x1)-f(x3.X())) != 0) { return .5; } else { return 0; } };
var y2 = board.create('point', [0, function() {
return y1.Y()-dist(); }],
{ visible : false });
var y3 = board.create('point', [0, function() {
return y1.Y()+dist(); }],
{ visible : false });
var endpoint1 = board.create('point', [0, 2],
{ name : '', fixed : true, size : 2, fillColor : 'white', strokeWidth : .5, strokeColor : 'black', showinfobox : false });
var endpoint2 = board.create('point', [0, 3],
{ name : '', fixed : true, size : 2, fillColor : 'black', strokeWidth : .5, strokeColor : 'black', showinfobox : false });
var v1 = board.create('segment', [x1, function() { return [x1.X(), y1.Y()]; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var v2 = board.create('line', [x2, function() { return [x2.X(), x2.Y()+1]; }],
{ strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var v3 = board.create('line', [x3, function() { return [x3.X(), x3.Y()+1]; }],
{ strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var delta = board.create('polygon', [function() { return [x2.X(), -5]; }, function() { return [x2.X(), 6]; },
function() { return [x3.X(), 6]; }, function() { return [x3.X(), -5]; }], {
highlight : false, fixed : true, vertices : { visible : false }, borders : { visible : false }, fillColor : '#446abd',
fillOpacity : .2
});
var h1 = board.create('segment', [y1, function() { return [x1.X(), y1.Y()]; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var h2 = board.create('line', [function() { return y2; }, function() { return [y2.X()+1, y2.Y()]; }],
{ strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var h3 = board.create('line', [function() { return y3; }, function() { return [y3.X()+1, y3.Y()]; }],
{ strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var epsilon = board.create('polygon', [[-5, 3.5],[10, 3.5],[10, 2.5], [-5, 2.5]], {
highlight : false, fixed : true, vertices : { visible : false }, borders : { visible : false }, fillColor : '#bd4444',
fillOpacity : .2
});
var txt = board.create('text', [4.2, -1.5, function() {
return ' '/*Math.max(Math.abs(y2.Y() - y1.Y()), Math.abs(y1.Y() - y3.Y())).toFixed(2)*/;
}], { strokeColor: '#bd4444', useMathJax : true, fixed : true });
board.unsuspendUpdate();
board.fullUpdate();
})();
'/*Math.max(Math.abs(y2.Y() - y1.Y()), Math.abs(y1.Y() - y3.Y())).toFixed(2)*/;
}], { strokeColor: '#bd4444', useMathJax : true, fixed : true });
board.unsuspendUpdate();
board.fullUpdate();
})();
Jatkuvien funktioiden ominaisuuksia
Tässä kappaleessa tutustutaan jatkuvien funktioiden tärkeimpiin ominaisuuksiin. Aloitamme jatkuvien funktioiden väliarvolauseella, joka tunnetaan myös nimellä Bolzanon lause. Tämän lauseen erään muotoilun mukaan jatkuva funktio saa kaikki arvot sen maksimin ja minimin väliltä. Intuitiivinen perustelu on se, että jatkuvan funtion kuvaaja on yhtenäinen viiva.
Väliarvolause.
Esimerkki 1.
Esimerkki 2 (kummallinen?).
By the Intermediate Value Theorem we have  for
for  or
or  . Similarly,
. Similarly,  for
for  or
or  , because:
, because:
 '}], { strokeColor : 'black', fontSize : 13, fixed : true });
var fright = board.create('text', [9.1, 7.6, function() { return '
'}], { strokeColor : 'black', fontSize : 13, fixed : true });
var fright = board.create('text', [9.1, 7.6, function() { return ' '}], { strokeColor : 'black', fontSize : 13, fixed : true });
var xleft = board.create('text', [1.1, -.1, function() { return '
'}], { strokeColor : 'black', fontSize : 13, fixed : true });
var xleft = board.create('text', [1.1, -.1, function() { return ' ' }], { strokeColor : 'black', fontSize : 13, fixed : true });
var xright = board.create('text', [9.1, -.1, function() { return '
' }], { strokeColor : 'black', fontSize : 13, fixed : true });
var xright = board.create('text', [9.1, -.1, function() { return ' ' }], { strokeColor : 'black', fontSize : 13, fixed : true });
l.on('drag', function() {
if(l.point1.Y() >= 7) {
l.point1.moveTo([0, 7]);
l.point2.moveTo([1, 7]);
}
else if(l.point1.Y() <= 4) {
l.point1.moveTo([0, 4]);
l.point2.moveTo([1, 4]);
}
});
var intersections = [];
intersections[0] = board.create('intersection', [l, g, 0], { name : '
' }], { strokeColor : 'black', fontSize : 13, fixed : true });
l.on('drag', function() {
if(l.point1.Y() >= 7) {
l.point1.moveTo([0, 7]);
l.point2.moveTo([1, 7]);
}
else if(l.point1.Y() <= 4) {
l.point1.moveTo([0, 4]);
l.point2.moveTo([1, 4]);
}
});
var intersections = [];
intersections[0] = board.create('intersection', [l, g, 0], { name : ' ', showinfobox : false,
label : { fontSize : 13, offset : [0, -15], strokeColor : 'blue', strokeWidth : .5} });
intersections[1] = board.create('intersection', [l, g, 1], { name : '
', showinfobox : false,
label : { fontSize : 13, offset : [0, -15], strokeColor : 'blue', strokeWidth : .5} });
intersections[1] = board.create('intersection', [l, g, 1], { name : ' ', showinfobox : false,
label : { fontSize : 13, offset : [8, 22], strokeColor : 'blue', strokeWidth : .5} });
intersections[2] = board.create('intersection', [l, g, 2], { name : '
', showinfobox : false,
label : { fontSize : 13, offset : [8, 22], strokeColor : 'blue', strokeWidth : .5} });
intersections[2] = board.create('intersection', [l, g, 2], { name : ' ', showinfobox : false,
label : { fontSize : 13, offset : [0, -15], strokeColor : 'blue', strokeWidth : .5} });
board.unsuspendUpdate();
})();
/* Example 1. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox17', {
boundingbox : [-3.5, 2.5, 3.5, -3.5],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return (Math.pow(x,5)-3*x-1); }
board.create('functiongraph', [f, -3.5, 3.5], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.fullUpdate();
})();
/* Example 2. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox18', {
boundingbox : [-3.2, 2.9, 3.2, -2.9],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return (x*x*x-x); }
board.create('functiongraph', [f, -3.2, -1], {
strokeColor : 'blue',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, -1, 0], {
strokeColor : 'red',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, 0, 1], {
strokeColor : 'blue',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, 1, 3.2], {
strokeColor : 'red',
strokeWidth : 2,
highlight : false
});
board.fullUpdate();
})();
', showinfobox : false,
label : { fontSize : 13, offset : [0, -15], strokeColor : 'blue', strokeWidth : .5} });
board.unsuspendUpdate();
})();
/* Example 1. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox17', {
boundingbox : [-3.5, 2.5, 3.5, -3.5],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return (Math.pow(x,5)-3*x-1); }
board.create('functiongraph', [f, -3.5, 3.5], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.fullUpdate();
})();
/* Example 2. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox18', {
boundingbox : [-3.2, 2.9, 3.2, -2.9],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return (x*x*x-x); }
board.create('functiongraph', [f, -3.2, -1], {
strokeColor : 'blue',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, -1, 0], {
strokeColor : 'red',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, 0, 1], {
strokeColor : 'blue',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, 1, 3.2], {
strokeColor : 'red',
strokeWidth : 2,
highlight : false
});
board.fullUpdate();
})();
Seuraavaksi osoitetaan, että suljetulla välillä jatkuva funktio on rajoitettu. Tässä on tärkeää, että kyseessä on nimenomaan suljettu väli. Lauseen jälkeinen esimerkki osoittaa, ettei väite pidä paikkaansa avoimille väleille.
Huom. Jos ![f\colon ]a,b[\to \mathbb{R} f\colon ]a,b[\to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/b877964696acedfc796cbe2d8af02c14.gif) on jatkuva, niin se ei välttämättä ole rajoitettu.
on jatkuva, niin se ei välttämättä ole rajoitettu.
Esimerkki 4.
Esimerkki 5.
Olkoon ![f\colon [-1,2] \to \mathbb{R} f\colon [-1,2] \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/7e4a05522be3c7dbc56233602cd169af.gif) ,
,
 Funktion määrittelyjoukko on
Funktion määrittelyjoukko on ![[-1,2] [-1,2]](https://mycourses.aalto.fi/filter/tex/pix.php/939b17134a44bb821e6c01efd044b32e.gif) . Funktion arvojoukon määrittämiseksi osoitetaan ensin, että funktio on vähenevä.
. Funktion arvojoukon määrittämiseksi osoitetaan ensin, että funktio on vähenevä.
Koska  ,
niin
,
niin  ja
ja
 Näin ollen oletuksesta
Näin ollen oletuksesta  seuraa
seuraa  , joten funktio
, joten funktio  on vahenevä.
on vahenevä.
Vähenevän funktion minimiarvo on välin päätepisteessä. Näin ollen funktion ![f:[-1,2] \to \mathbb{R} f:[-1,2] \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/46f6b5865e82341801d84f074d5275a9.gif) minimi on
minimi on
 Vastaavasti suurin arvo on väli alkupisteessä, joten funktion
Vastaavasti suurin arvo on väli alkupisteessä, joten funktion ![f:[-1,2] \to \mathbb{R} f:[-1,2] \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/46f6b5865e82341801d84f074d5275a9.gif) maksimi on
maksimi on

Polynomina funktio  on jatkuva, joten se saa kaikki arvot maksimin ja minimin välillä. Näin ollen funktion
on jatkuva, joten se saa kaikki arvot maksimin ja minimin välillä. Näin ollen funktion  arvojoukko on
arvojoukko on ![[-7, 5] [-7, 5]](https://mycourses.aalto.fi/filter/tex/pix.php/e8699196563455925f438ba7d4253294.gif) .
.
Esimerkki 6.
Olkoon  polynomi. Silloin
polynomi. Silloin  on jatkuva joukossa
on jatkuva joukossa  ja lauseen 7 nojalla myös rajoitettu jokaisella suljetulla välillä
ja lauseen 7 nojalla myös rajoitettu jokaisella suljetulla välillä ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) , kun
, kun  . Lauseen 3 perusteella funktiolla
. Lauseen 3 perusteella funktiolla  on maksimi ja minimi
on maksimi ja minimi ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) .
.
Huom. Lause 8 liittyy väliarvolauseeseen seuraavalla tavalla:
Jos ![f\colon [a,b]\to \mathbb{R} f\colon [a,b]\to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/fb88b7c4cd82a1b35ba68754b552ae78.gif) on jatkuva, niin on olemassa pisteet
on jatkuva, niin on olemassa pisteet ![x_1,x_2\in [a,b] x_1,x_2\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/e19d698696d7ffab6b38c33a403d0f82.gif) , joille funktion arvojoukko on muotoa
, joille funktion arvojoukko on muotoa ![f([a,b])=[f(x_1),f(x_2)] f([a,b])=[f(x_1),f(x_2)]](https://mycourses.aalto.fi/filter/tex/pix.php/d38dd7ed255a633b5f3b32a8b4251475.gif) .
.
4. Derivaatta
Sisältö
- Derivaatta
- Derivaatan ominaisuudet
- Trigonometristen funktioiden derivaatat
- Ketjusääntö
- Ääriarvot
Derivaatta
Tässä luvussa käsitellään derivaattaa ja sen ominaisuuksia. Aloitetaan esimerkillä, joka johdattelee derivaatan määritelmää.
Esimerkki 0.
Alla oleva kuvaaja kertoo, kuinka kauaksi pyöräilijä on edennyt lähtöpisteestään.
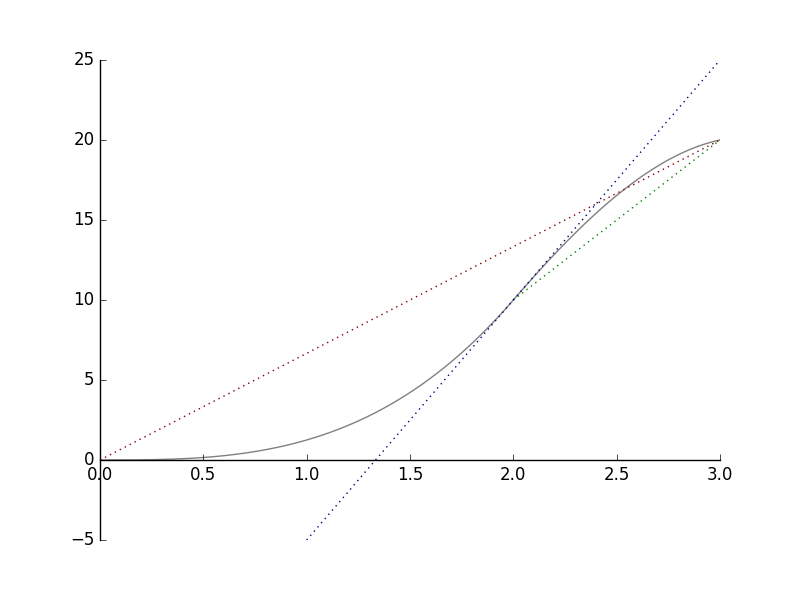
a) Tarkastellaan punaista viivaa. Huomataan, että kolmen tunnin aikana pyöräilijä on edennyt  km. Hänen keskinopeutensa on
km. Hänen keskinopeutensa on  km/h.
km/h.
b) Tarkastellaan sitten vihreää viivaa. Huomataan, että kolmannen tunnin aikana pyöräilijä on edennyt  km. Tällä aikavälillä hänen keskinopeutensa on siis
km. Tällä aikavälillä hänen keskinopeutensa on siis  km/h.
km/h.
Huomaa, että punaisen viivan kulmakerroin on  ja vihreän viivan kulmakerroin on
ja vihreän viivan kulmakerroin on  . Lukuarvot ovat samat kuin vastaavat keskinopeudet.
. Lukuarvot ovat samat kuin vastaavat keskinopeudet.
c) Tarkastellaan vielä sinistä viivaa. Se on kuvaajan tangentti kohdassa  h. Kuten keskinopeuksien kohdalla, voidaan päätellä, että kaksi tuntia lähdön jälkeen pyöräilijän nopeus oli
h. Kuten keskinopeuksien kohdalla, voidaan päätellä, että kaksi tuntia lähdön jälkeen pyöräilijän nopeus oli  km/h
km/h  km/h.
km/h.
Siirrytään sitten yleiseen määritelmään:
Määritelmä: Derivaatta
Olkoon  . Funktion
. Funktion  derivaatta pisteessä
derivaatta pisteessä  on
on  Jos
Jos  on olemassa, niin
on olemassa, niin  on derivoituva pisteessä
on derivoituva pisteessä  .
.
Huom: Koska  , niin
, niin  , joten määritelmä voidaan kirjoittaa myös muodossa
, joten määritelmä voidaan kirjoittaa myös muodossa 
Tulkinta. Tarkastellaan käyrää  . Jos piirretään suora viiva pisteiden
. Jos piirretään suora viiva pisteiden  ja
ja  kautta, niin tämän suoran kulmakerroin on
kautta, niin tämän suoran kulmakerroin on  Kun
Kun  , tämä suora sivuaa käyrää
, tämä suora sivuaa käyrää  pisteessä
pisteessä  . Tämä suora on käyrän
. Tämä suora on käyrän  tangentti pisteessä
tangentti pisteessä  ja sen kulmakerroin on
ja sen kulmakerroin on  joka on funktion
joka on funktion  derivaatta pisteessä
derivaatta pisteessä  . Tangentin yhtälö on siis muotoa
. Tangentin yhtälö on siis muotoa 
Kokeile. Tutki tangentin muuttumista siirtämällä sivuamispistettä.
Esimerkki 1.
Esimerkki 2.
Esimerkki 3.
Olkoon  ,
,  . Onko
. Onko  derivoituva pisteessä
derivoituva pisteessä  ?
?
Kuvaajalla  ei ole tangenttia pisteessä
ei ole tangenttia pisteessä  :
:  Näin ollen
Näin ollen  ei ole olemassa.
ei ole olemassa.
Johtopäätös. Funktio  ei ole derivoituva pisteessä
ei ole derivoituva pisteessä  .
.
Huom. Olkoon  . Jos
. Jos  on olemassa kaikissa pisteissä
on olemassa kaikissa pisteissä  , niin saadaan uusi funktio
, niin saadaan uusi funktio  . Merkitään:
. Merkitään:
| (1) |  |
=  , , |
|
| (2) |  |
=  |
=  , , |
| (3) |  |
=  |
=  , , |
| (4) |  |
=  |
=  , , |
| ... |
Tässä  on funktion
on funktion  toisen kertaluvun derivaatta pisteessä
toisen kertaluvun derivaatta pisteessä  ,
,  on kolmannen kertaluvun derivaatta jne.
on kolmannen kertaluvun derivaatta jne.
Yleisesti merkitään \begin{eqnarray} C^n\bigl( ]a,b[\bigr) =\{ f\colon \, ]a,b[\, \to \mathbb{R} & \mid & f \text{ on } n \text{ kertaa derivoituva välillä } ]a,b[ \nonumber \\ & & \text{ ja } f^{(n)} \text{ on jatkuva}\}. \nonumber \end{eqnarray} Tällaiset funktiot ovat n kertaa jatkuvasti derivoituvia.
Esimerkki 4.
Linearisointi ja differentiaali
 missä oikean puolen lauseke on funktion
missä oikean puolen lauseke on funktion  linearisointi tai differentiaali pisteessä
linearisointi tai differentiaali pisteessä  . Differentiaalia merkitään
. Differentiaalia merkitään  . Linearisoinnin kuvaaja
. Linearisoinnin kuvaaja  on funktion kuvaajan tangentti pisteessä
on funktion kuvaajan tangentti pisteessä  . Differentiaalin varsinainen merkitys tulee näkyviin vasta usean muuttujan funktioiden yhteydessä, eikä sitä tarvita tällä kurssilla.
. Differentiaalin varsinainen merkitys tulee näkyviin vasta usean muuttujan funktioiden yhteydessä, eikä sitä tarvita tällä kurssilla.Derivaatan ominaisuudet
Seuraavaksi käydään läpi derivaatan tärkeimmät ominaisuudet. Näiden avulla voidaan selvittää tärkeimpien alkeisfunktioiden derivaatat.
Jatkuvuus ja derivaatta
Derivointisäännöt
For  we repeteadly apply the product rule, and obtain
we repeteadly apply the product rule, and obtain 
The case of negative  is obtained from this and the product rule applied to the identity
is obtained from this and the product rule applied to the identity  .
.
From the power rule we obtain a formula for the derivative of a polynomial. Let  where
where  . Then
. Then 
Suppose that  is differentiable at
is differentiable at  and
and  . We determine
. We determine 
From the definition we obtain: 
The one-sided limits of the difference quotient have different signs at a local extremum. For example, for a local maximum it holds that \begin{eqnarray} \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative} }{\text{positive}}&\le& 0, \text{ when } h>0, \nonumber \\ \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative}}{\text{negative}}&\ge& 0, \text{ when } h<0 \nonumber \end{eqnarray} and  is so small that
is so small that  is a maximum on the interval
is a maximum on the interval ![[x_0-h,x_0+h] [x_0-h,x_0+h]](https://mycourses.aalto.fi/filter/tex/pix.php/fa82e5aaac1e1a7465724ab32e282839.gif) .
.
Trigonometristen funktioiden derivaatat
Tässä kappaleessa johdetaan funktioiden  ,
,  ja
ja  derivaatat.
derivaatat.
Ketjusääntö
Ketjusäännöllä tarkoitetaan yhdistettyjen funktioiden derivoimissääntöä. Tämä termin tausta selittyy paremmin usean muuttujan funktioiden (osittais)derivaattojen yhteydessä.
Ketjusääntö.
Todistus.Esimerkki 1.
Esimerkki 2.
Esimerkki 3.
Ääriarvot
Tässä kappaleessa tarkastellaan derivaatan käyttöä ääriarvotehtävissä.
Määritelmä: Paikallinen maksimi ja minimi
Funktiolla  on paikallinen maksimi pisteessä
on paikallinen maksimi pisteessä  , jos on olemassa sellainen
, jos on olemassa sellainen  , että
, että  aina kun
aina kun  ja
ja  .
.
Vastaavasti, funktiolla  on paikallinen minimi pisteessä
on paikallinen minimi pisteessä  , jos on olemassa sellainen
, jos on olemassa sellainen  , että
, että  aina kun
aina kun  ja
ja  .
.
Funktion paikallinen ääriarvo tarkoittaa joko paikallista maksimia tai paikallista minimiä.
Huom. Jos  on paikallinen maksimikohta ja
on paikallinen maksimikohta ja  on olemassa, niin
on olemassa, niin
 Näin ollen
Näin ollen  .
.
Näin saadaan:
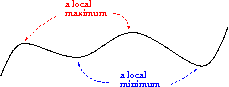
Esimerkki 1.
Globaali maksimi ja minimi
Käytännössä paikallisia ääriarvoja voi esiintyä kolmea eri tyyppiä olevissa pisteissä:
derivaatan nollakohdat
määrittelyvälin päätepisteet
määrittelyvälin sisällä olevat kohdat, joissa funktio ei ol e derivoituva
Jos tiedetään etukäteen, että funktiolla on maksimi tai minimi, niin aluksi etsitään kaikki mahdolliset paikalliset ääriarvokohdat (yllä oleva lista), lasketaan funktion arvot näissä pisteissä ja valitaan näistä arvoista suurin tai pienin.
Esimerkki 2.
Määritetään funktion ![f\colon [0,2]\to \mathbf{R} f\colon [0,2]\to \mathbf{R}](https://mycourses.aalto.fi/filter/tex/pix.php/ee77c8a9721b9494f327d61422eb2068.gif) ,
,  , suurin ja pienin arvo. Koska kyseessä on suljetulla välillä jatkuva funktio, niin sillä on maksimi ja minimi. Funktio on myös derivoituva, joten riittää tutkia välin päätepisteet ja välin sisälle jäävät derivaatan nollakohdat.
, suurin ja pienin arvo. Koska kyseessä on suljetulla välillä jatkuva funktio, niin sillä on maksimi ja minimi. Funktio on myös derivoituva, joten riittää tutkia välin päätepisteet ja välin sisälle jäävät derivaatan nollakohdat.
Derivaatan nollakohdat:  . Koska
. Koska ![-\sqrt{2}\not\in [0,2] -\sqrt{2}\not\in [0,2]](https://mycourses.aalto.fi/filter/tex/pix.php/601d5044bf746b9e7af4678c2c3463a1.gif) , täytyy laskea funktion arvot vain kolmessa pisteessä:
, täytyy laskea funktion arvot vain kolmessa pisteessä:  ,
,  ja
ja  . Näiden avulla päätellään funktion pienimmäksi arvoksi
. Näiden avulla päätellään funktion pienimmäksi arvoksi  ja suurimmaksi arvoksi
ja suurimmaksi arvoksi  .
.
Seuraavaksi esitetään eräs tärkeimmistä derivoituvia funktioita koskevista tuloksista.
Lause 2.
(Derivoituvien funktioiden väliarvolause). Olkoon ![f\colon [a,b]\to \mathbb{R} f\colon [a,b]\to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/fb88b7c4cd82a1b35ba68754b552ae78.gif) jatkuva suljetulla välillä
jatkuva suljetulla välillä ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) ja derivoituva avoimella välillä
ja derivoituva avoimella välillä  . Silloin
. Silloin
 jollekin
jollekin 
Let  be continuous in the interval
be continuous in the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) and differentiable in the interval
and differentiable in the interval  . Let us define
. Let us define

Now  and
and  is differentiable in the interval
is differentiable in the interval  . According to Rolle's Theorem, there exists
. According to Rolle's Theorem, there exists  such that
such that  . Hence
. Hence

Tärkeitä seurauksia:
Lause 3.
Esimerkki 3.
Esimerkki 4.
Määritetään sellainen suorakulmio, jonka pinta-ala on  ja jonka piiri on mahdollisimman pieni.
ja jonka piiri on mahdollisimman pieni.
Olkoot  ja
ja  suorakulmion sivut. Silloin
suorakulmion sivut. Silloin  , joten
, joten  . Suorakulmion piiri on
. Suorakulmion piiri on
 Etsitään funktion
Etsitään funktion  pienin arvo. Funktio
pienin arvo. Funktio  on derivoituva, kun
on derivoituva, kun  , ja osamäärän derivoimissäännön mukaan
, ja osamäärän derivoimissäännön mukaan
 Nyt
Nyt  , kun
, kun
 mutta ehdon
mutta ehdon  perusteella vain
perusteella vain  on mahdollinen. Muodotetaan kulkukaavio:
on mahdollinen. Muodotetaan kulkukaavio:
 |
 |
|
|---|---|---|
 |
 |
 |
 |
väh. | kasv. |
Koska funktio  on jatkuva, niin se saavuttaa miniminsä pisteessä
on jatkuva, niin se saavuttaa miniminsä pisteessä  . Tällöin sen toisen sivun pituus on
. Tällöin sen toisen sivun pituus on  .
.
Esimerkki 5.
Tehtävänä on muodostaa suoran ympyräsylinterin muotoinen yhden litran mitta (ilman kantta) niin, että materiaalia tarvitaan mahdollisimman vähän.
Olkoon  sylinterin poikkileikkauksen säde ja
sylinterin poikkileikkauksen säde ja  sylinterin korkeus. Sylinterin tilavuus on
sylinterin korkeus. Sylinterin tilavuus on  dm
dm , joten saadaan yhtälö
, joten saadaan yhtälö  . Tästä voidaan ratkaista
. Tästä voidaan ratkaista

Tarvittavan materiaalin määrää kuvaa pinta-ala

Määritellään siis  asettamalla
asettamalla
 Tavoitteena on etsiä funktion
Tavoitteena on etsiä funktion  minimi, ja kyseessä on alueessa
minimi, ja kyseessä on alueessa  derivoituva funktio. Derivaataksi saadaan
derivoituva funktio. Derivaataksi saadaan
 Nyt
Nyt  , kun
, kun
![\begin{aligned}2\pi r^3 - 2 &= 0 \\
2\pi r^3 &= 2 \\
r^3 &= \frac{1}{\pi} \\
r &= \frac{1}{\sqrt[3]{\pi}}.\end{aligned} \begin{aligned}2\pi r^3 - 2 &= 0 \\
2\pi r^3 &= 2 \\
r^3 &= \frac{1}{\pi} \\
r &= \frac{1}{\sqrt[3]{\pi}}.\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/ffb8cf82115510a023a5408e30bf2b57.gif)
Muodostetaan kulkukaavio:
 |
![r>\frac{1}{\sqrt[3]{\pi}} r>\frac{1}{\sqrt[3]{\pi}}](https://mycourses.aalto.fi/filter/tex/pix.php/70296efeaa006fb5cd9c2f29b5d0a0e2.gif) |
|
|---|---|---|
 |
 |
 |
 |
väh. | kasv. |
Koska funktio  on jatkuva, niin sen pienin arvo saavutetaan kohdassa
on jatkuva, niin sen pienin arvo saavutetaan kohdassa ![r= \frac{1}{\sqrt[3]{\pi}} \approx 0.683 r= \frac{1}{\sqrt[3]{\pi}} \approx 0.683](https://mycourses.aalto.fi/filter/tex/pix.php/ef4b63276241174d0f518a6b4301d081.gif) . Silloin
. Silloin
![h = \frac{1}{\pi r^2} = \frac{1}{\pi \left(\frac{1}{\sqrt[3]{\pi}}\right)^2} = \frac{1}{\frac{\pi}{\pi^{2/3}}} = \frac{1}{\sqrt[3]{\pi}} \approx 0.683. h = \frac{1}{\pi r^2} = \frac{1}{\pi \left(\frac{1}{\sqrt[3]{\pi}}\right)^2} = \frac{1}{\frac{\pi}{\pi^{2/3}}} = \frac{1}{\sqrt[3]{\pi}} \approx 0.683.](https://mycourses.aalto.fi/filter/tex/pix.php/8af221027cf46db4d652e5781ac056d2.gif)
Näin ollen optimaalisen mitan poikkileikkauksen läpimitta on  dm
dm  dm
dm  cm ja korkeus
cm ja korkeus  dm
dm  cm.
cm.
 ',
label : { strokeColor : 'blue' }
});
var t = board.create('tangent', [g1], {
strokeWidht : 2,
strokeOpacity : .8
});
var text1 = board.create('text', [-4, 5, function() { return '
',
label : { strokeColor : 'blue' }
});
var t = board.create('tangent', [g1], {
strokeWidht : 2,
strokeOpacity : .8
});
var text1 = board.create('text', [-4, 5, function() { return ' '}], {
useMathJax : true,
fontSize : 14,
strokeColor : 'black'
});
var text2 = board.create('text', [-4, 4, function() {
var k = t.getSlope();
var b = g1.Y()-k*g1.X();
var temp = '';
if(k == 0) {
temp = '
'}], {
useMathJax : true,
fontSize : 14,
strokeColor : 'black'
});
var text2 = board.create('text', [-4, 4, function() {
var k = t.getSlope();
var b = g1.Y()-k*g1.X();
var temp = '';
if(k == 0) {
temp = ' ';
} else {
if(b < 0) {
temp = '
';
} else {
if(b < 0) {
temp = ' ';
} else {
temp = '
';
} else {
temp = ' ';
}
}
return temp;
}
], {
useMathJax : true,
fontSize : 14,
strokeColor : 'blue'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox : [-3.5, 3, 3.5, -3],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0],[1, 0]], {
ticks : { majorHeight : 5 }
});
var yaxis = board.create('axis' ,[[0, 0],[0, 1]], {
ticks : { majorHeight : 5}
});
var f = function(x) { return x*x*x+1; }
var graph = board.create('functiongraph', [f, -3.5, 3.5], {
strokeWidth : 1.5,
strokeColor : 'black'
});
var g1 = board.create('glider', [1, f(1), graph], { strokeColor : 'black', size : 2, fillColor : 'red', name : '' });
var t = board.create('tangent', [g1], { strokeColor : 'red', strokeWidth : 1.5 });
var a = board.create('segment', [[function() { return g1.X() }, function() { return g1.Y()-t.getSlope(); }],
[function() { return g1.X()-1; }, function() { return g1.Y()-t.getSlope() }]], {
strokeWidth : 2,
strokeOpacity : .8,
dash : 1,
highlight : false
});
var b = board.create('segment', [[ function() { return g1.X(); }, function() { return g1.Y(); }],
[ function() { return a.point1.X(); }, function() { return a.point1.Y(); } ]], {
strokeWidth : 2,
strokeOpacity : .8,
dash : 1,
highlight : false
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox04', {
boundingbox : [-5, 5, 5, -2],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return Math.abs(x); }
board.create('functiongraph', [f, -5, 5], {
strokeWidth : 2,
strokeColor : '#2183de',
highlight : false
});
board.create('text', [1.5, 1.2, function() { return '
';
}
}
return temp;
}
], {
useMathJax : true,
fontSize : 14,
strokeColor : 'blue'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox : [-3.5, 3, 3.5, -3],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0],[1, 0]], {
ticks : { majorHeight : 5 }
});
var yaxis = board.create('axis' ,[[0, 0],[0, 1]], {
ticks : { majorHeight : 5}
});
var f = function(x) { return x*x*x+1; }
var graph = board.create('functiongraph', [f, -3.5, 3.5], {
strokeWidth : 1.5,
strokeColor : 'black'
});
var g1 = board.create('glider', [1, f(1), graph], { strokeColor : 'black', size : 2, fillColor : 'red', name : '' });
var t = board.create('tangent', [g1], { strokeColor : 'red', strokeWidth : 1.5 });
var a = board.create('segment', [[function() { return g1.X() }, function() { return g1.Y()-t.getSlope(); }],
[function() { return g1.X()-1; }, function() { return g1.Y()-t.getSlope() }]], {
strokeWidth : 2,
strokeOpacity : .8,
dash : 1,
highlight : false
});
var b = board.create('segment', [[ function() { return g1.X(); }, function() { return g1.Y(); }],
[ function() { return a.point1.X(); }, function() { return a.point1.Y(); } ]], {
strokeWidth : 2,
strokeOpacity : .8,
dash : 1,
highlight : false
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox04', {
boundingbox : [-5, 5, 5, -2],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return Math.abs(x); }
board.create('functiongraph', [f, -5, 5], {
strokeWidth : 2,
strokeColor : '#2183de',
highlight : false
});
board.create('text', [1.5, 1.2, function() { return ' '; }], {
useMathJax : true,
strokeColor : '#2183de',
fontSize : 13,
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox05', {
boundingbox : [-1.7, 10.1, 1.7, -10.1],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 5; };
var f = function(x) { return (x*x*x*x-2)*(2*x+1); }
board.create('functiongraph', [f, -1.7, 1.7], {
strokeWidth : 2.5,
strokeColor : 'black',
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox06', {
boundingbox : [-6.1, 6.5, 6.1, -6.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return x*x*x/(1+x*x); }
board.create('functiongraph', [f, -6.1, 6.1], {
strokeWidth : 2.5,
strokeColor : 'black',
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox07', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.sin(x); }
var df = function(x) { return Math.cos(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'red'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox08', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.cos(x); }
var df = function(x) { return Math.sin(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox09', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.tan(x); }
var df = function(x) { return 1/Math.pow(Math.cos(x),2); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'green'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox10', {
boundingbox : [-3.2, 4.5, 4.8, -2.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(2*x*x-1, 3); }
var df = function(x) { return 6*Math.pow(2*x*x-1, 2); }
board.create('functiongraph', [f, 0, 4.8], {
strokeWidth : 1.5,
strokeColor : 'green'
});
board.create('functiongraph', [df, 0, 4.8], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox11', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.sin(3*x); }
var df = function(x) { return 3*Math.cos(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'red'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox12', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(Math.cos(2*x), 3); }
var df = function(x) { return -6*Math.sin(2*x)*Math.pow(Math.cos(2*x), 2); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox13', {
boundingbox : [-4.73, 4.2, 4.73, -4.2],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return x*x*x-3*x+1; }
var df = function(x) { return 3*x*x-3; }
board.create('functiongraph', [f, -3.2, 3.2], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -3.2, 3.2], {
strokeWidth : 1.5,
strokeColor : 'red'
});
var p = [];
p[0] = board.create('point', [-1, f(-1)]);
p[1] = board.create('point', [-1, df(-1)]);
p[2] = board.create('point', [1, f(1)]);
p[3] = board.create('point', [1, df(1)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
strokeColor : 'black',
size : .5,
name : '',
fillColor : 'black',
fixed : true
});
}
board.create('segment', [p[0],p[1]], {
strokeColor : 'black',
dash : 1,
highlight : false
});
board.create('segment', [p[2],p[3]], {
strokeColor : 'black',
dash : 1,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox14', {
boundingbox : [-6.76, 1, 6.76, -11],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(x, 4)/4-2*x*x-7; }
board.create('functiongraph', [f, -5.6, 5.6], {
strokeWidth : 1.5,
strokeColor : 'black'
});
var p = [];
p[0] = board.create('point', [-2, 0], {
});
p[1] = board.create('point', [-2, f(-2)], {
});
p[2] = board.create('point', [0, 0], {
});
p[3] = board.create('point', [0, f(0)], {
});
p[4] = board.create('point', [2, 0], {
});
p[5] = board.create('point', [2, f(2)], {
});
for(var i=0; i < p.length; i++) {
p[i].setAttribute({ visible : false });
}
board.create('segment', [p[0],p[1]], {
strokeColor : 'red',
highlight : false,
fixed : true
});
board.create('segment', [p[2],p[3]], {
strokeColor : 'blue',
highlight : false,
fixed : true
});
board.create('segment', [p[4],p[5]], {
strokeColor : 'red',
highlight : false,
fixed : true
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox15', {
boundingbox : [-1, 15, 10, -1.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return (2*x*x+18)/x; }
var graph = board.create('functiongraph', [f, -1, 15.9], {
strokeColor : 'black',
strokeWidth : 2.5,
highlight : false
});
var p = [];
p[0] = board.create('point', [3, 0]);
p[1] = board.create('point', [3,f(3)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
name : '',
size : 1,
strokeColor : 'black',
strokeWidth : .5,
fixed : true });
}
board.create('segment', [p[0], p[1]], {
dash : 1,
strokeWidth : 2,
strokeColor : 'red',
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox16', {
boundingbox : [-1, 13, 5, -1],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return Math.PI*x*x+2/x; }
var graph = board.create('functiongraph', [f, 0, 5], {
strokeColor : 'black',
strokeWidth : 2.5,
highlight : false
});
var p = [];
var a = 1/Math.pow(Math.PI,1/3);
p[0] = board.create('point', [a, 0]);
p[1] = board.create('point', [a, f(a)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
name : '',
size : 1,
strokeColor : 'black',
fixed : true });
}
board.create('segment', [p[0], p[1]], {
dash : 1,
strokeWidth : 2,
strokeColor : 'red',
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox17', {
boundingbox : [-4, 4, 4, -4],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var s = board.create('slider', [[-3.5, 3.5], [-.5, 3.5], [-10, 0, 10]],{
suffixLabel : '
'; }], {
useMathJax : true,
strokeColor : '#2183de',
fontSize : 13,
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox05', {
boundingbox : [-1.7, 10.1, 1.7, -10.1],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 5; };
var f = function(x) { return (x*x*x*x-2)*(2*x+1); }
board.create('functiongraph', [f, -1.7, 1.7], {
strokeWidth : 2.5,
strokeColor : 'black',
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox06', {
boundingbox : [-6.1, 6.5, 6.1, -6.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return x*x*x/(1+x*x); }
board.create('functiongraph', [f, -6.1, 6.1], {
strokeWidth : 2.5,
strokeColor : 'black',
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox07', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.sin(x); }
var df = function(x) { return Math.cos(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'red'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox08', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.cos(x); }
var df = function(x) { return Math.sin(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox09', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.tan(x); }
var df = function(x) { return 1/Math.pow(Math.cos(x),2); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'green'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox10', {
boundingbox : [-3.2, 4.5, 4.8, -2.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(2*x*x-1, 3); }
var df = function(x) { return 6*Math.pow(2*x*x-1, 2); }
board.create('functiongraph', [f, 0, 4.8], {
strokeWidth : 1.5,
strokeColor : 'green'
});
board.create('functiongraph', [df, 0, 4.8], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox11', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.sin(3*x); }
var df = function(x) { return 3*Math.cos(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'red'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox12', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(Math.cos(2*x), 3); }
var df = function(x) { return -6*Math.sin(2*x)*Math.pow(Math.cos(2*x), 2); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox13', {
boundingbox : [-4.73, 4.2, 4.73, -4.2],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return x*x*x-3*x+1; }
var df = function(x) { return 3*x*x-3; }
board.create('functiongraph', [f, -3.2, 3.2], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -3.2, 3.2], {
strokeWidth : 1.5,
strokeColor : 'red'
});
var p = [];
p[0] = board.create('point', [-1, f(-1)]);
p[1] = board.create('point', [-1, df(-1)]);
p[2] = board.create('point', [1, f(1)]);
p[3] = board.create('point', [1, df(1)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
strokeColor : 'black',
size : .5,
name : '',
fillColor : 'black',
fixed : true
});
}
board.create('segment', [p[0],p[1]], {
strokeColor : 'black',
dash : 1,
highlight : false
});
board.create('segment', [p[2],p[3]], {
strokeColor : 'black',
dash : 1,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox14', {
boundingbox : [-6.76, 1, 6.76, -11],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(x, 4)/4-2*x*x-7; }
board.create('functiongraph', [f, -5.6, 5.6], {
strokeWidth : 1.5,
strokeColor : 'black'
});
var p = [];
p[0] = board.create('point', [-2, 0], {
});
p[1] = board.create('point', [-2, f(-2)], {
});
p[2] = board.create('point', [0, 0], {
});
p[3] = board.create('point', [0, f(0)], {
});
p[4] = board.create('point', [2, 0], {
});
p[5] = board.create('point', [2, f(2)], {
});
for(var i=0; i < p.length; i++) {
p[i].setAttribute({ visible : false });
}
board.create('segment', [p[0],p[1]], {
strokeColor : 'red',
highlight : false,
fixed : true
});
board.create('segment', [p[2],p[3]], {
strokeColor : 'blue',
highlight : false,
fixed : true
});
board.create('segment', [p[4],p[5]], {
strokeColor : 'red',
highlight : false,
fixed : true
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox15', {
boundingbox : [-1, 15, 10, -1.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return (2*x*x+18)/x; }
var graph = board.create('functiongraph', [f, -1, 15.9], {
strokeColor : 'black',
strokeWidth : 2.5,
highlight : false
});
var p = [];
p[0] = board.create('point', [3, 0]);
p[1] = board.create('point', [3,f(3)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
name : '',
size : 1,
strokeColor : 'black',
strokeWidth : .5,
fixed : true });
}
board.create('segment', [p[0], p[1]], {
dash : 1,
strokeWidth : 2,
strokeColor : 'red',
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox16', {
boundingbox : [-1, 13, 5, -1],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return Math.PI*x*x+2/x; }
var graph = board.create('functiongraph', [f, 0, 5], {
strokeColor : 'black',
strokeWidth : 2.5,
highlight : false
});
var p = [];
var a = 1/Math.pow(Math.PI,1/3);
p[0] = board.create('point', [a, 0]);
p[1] = board.create('point', [a, f(a)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
name : '',
size : 1,
strokeColor : 'black',
fixed : true });
}
board.create('segment', [p[0], p[1]], {
dash : 1,
strokeWidth : 2,
strokeColor : 'red',
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox17', {
boundingbox : [-4, 4, 4, -4],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var s = board.create('slider', [[-3.5, 3.5], [-.5, 3.5], [-10, 0, 10]],{
suffixLabel : '  ',
label : { useMathJax : true, fontSize : 13 },
fillColor : '#31d490',
withTicks : false,
precision : 2,
snapWidth : 1
});
var f = function(x) { return x*x*x-x; }
var g = function(x) { return s.Value()*(x*x*x-x); }
var graph1 = board.create('functiongraph', [f, -4, 4], {
strokeColor : '#4260f5',
strokeWidth : 2.5,
highlight : false,
strokeOpacity : 0.6,
highlight : false
});
var graph2 = board.create('functiongraph', [g, -4, 4], {
strokeColor : '#31d490',
strokeWidth : 2.5,
highlight : false,
strokeOpacity : .8,
highlight : false
});
var g0 = board.create('glider', [0, 0, xaxis], {
name : '
',
label : { useMathJax : true, fontSize : 13 },
fillColor : '#31d490',
withTicks : false,
precision : 2,
snapWidth : 1
});
var f = function(x) { return x*x*x-x; }
var g = function(x) { return s.Value()*(x*x*x-x); }
var graph1 = board.create('functiongraph', [f, -4, 4], {
strokeColor : '#4260f5',
strokeWidth : 2.5,
highlight : false,
strokeOpacity : 0.6,
highlight : false
});
var graph2 = board.create('functiongraph', [g, -4, 4], {
strokeColor : '#31d490',
strokeWidth : 2.5,
highlight : false,
strokeOpacity : .8,
highlight : false
});
var g0 = board.create('glider', [0, 0, xaxis], {
name : ' ',
size : 4,
strokeColor : 'black',
strokeWidth : .7,
fillColor : '#42f57e',
label : { useMathJax : true }
});
var g1 = board.create('glider', [0, 0, graph1], {
name : '',
size : 2,
strokeWidth : .7,
strokeColor : 'black',
fillColor : '#42f57e',
fixed : true,
highlight : false
});
var l1 = board.create('line', [g0, g1], {
straightFirst : false,
strokeColor : '#42f57e',
dash : 1,
highlight : false
});
var g2 = board.create('glider', [0, 0, graph2], {
visible : false
});
var t1 = board.create('tangent', [g1], {
strokeColor : '#4260f5',
strokeWidth : 2.5,
strokeOpacity : 0.6,
highlight : false
});
var t2 = board.create('tangent', [g2], {
strokeColor : '#31d490',
strokeWidth : 2.5,
strokeOpacity : .8,
highlight : false
});
board.create('text', [-3.5, 2.8, function() { return '
',
size : 4,
strokeColor : 'black',
strokeWidth : .7,
fillColor : '#42f57e',
label : { useMathJax : true }
});
var g1 = board.create('glider', [0, 0, graph1], {
name : '',
size : 2,
strokeWidth : .7,
strokeColor : 'black',
fillColor : '#42f57e',
fixed : true,
highlight : false
});
var l1 = board.create('line', [g0, g1], {
straightFirst : false,
strokeColor : '#42f57e',
dash : 1,
highlight : false
});
var g2 = board.create('glider', [0, 0, graph2], {
visible : false
});
var t1 = board.create('tangent', [g1], {
strokeColor : '#4260f5',
strokeWidth : 2.5,
strokeOpacity : 0.6,
highlight : false
});
var t2 = board.create('tangent', [g2], {
strokeColor : '#31d490',
strokeWidth : 2.5,
strokeOpacity : .8,
highlight : false
});
board.create('text', [-3.5, 2.8, function() { return ' '; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [-3.5, 2.3, function() { return '
'; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [-3.5, 2.3, function() { return ' '; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [1.5, -2, function() { return '
'; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [1.5, -2, function() { return ' '; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [1.5, -2.5, function() { return '
'; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [1.5, -2.5, function() { return ' '; }],{
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
g0.on('drag', function() {
var x = g0.X();
g1.moveTo([x, f(x)]);
g2.moveTo([x, g(x)]);
board.update();
});
board.fullUpdate();
})();
"; }
],
{
fontSize : 15
});*/
board.unsuspendUpdate();
}
}
function addDerivative() {
if (JXG.isFunction(f)) {
board.create('functiongraph',[JXG.Math.Numerics.D(f),
function(){
var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[0,0],board);
return c.usrCoords[1];
},
function(){
var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[board.canvasWidth,0],board);
return c.usrCoords[1];
}], {
dash : 2,
strokeWidth : 2,
strokeColor : '#3ac946'
});
}
}
document.getElementById('plot').onclick = plotter;
document.getElementById('clear all').onclick = clearAll;
document.getElementById('add tangent').onclick = addTangent;
document.getElementById('add Derivative').onclick = addDerivative;
})();
'; }],{
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
g0.on('drag', function() {
var x = g0.X();
g1.moveTo([x, f(x)]);
g2.moveTo([x, g(x)]);
board.update();
});
board.fullUpdate();
})();
"; }
],
{
fontSize : 15
});*/
board.unsuspendUpdate();
}
}
function addDerivative() {
if (JXG.isFunction(f)) {
board.create('functiongraph',[JXG.Math.Numerics.D(f),
function(){
var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[0,0],board);
return c.usrCoords[1];
},
function(){
var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[board.canvasWidth,0],board);
return c.usrCoords[1];
}], {
dash : 2,
strokeWidth : 2,
strokeColor : '#3ac946'
});
}
}
document.getElementById('plot').onclick = plotter;
document.getElementById('clear all').onclick = clearAll;
document.getElementById('add tangent').onclick = addTangent;
document.getElementById('add Derivative').onclick = addDerivative;
})();
5. Taylor-polynomi
Taylor-polynomi
Määritelmä: Taylor-polynomi
Olkoon  funktio, joka on
funktio, joka on  kertaa derivoituva pisteessä
kertaa derivoituva pisteessä  . Tällöin Taylor-polynomi \begin{align}
P_n(x)&=P_n(x;x_0)\\\
&=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+ \\
& \dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\
&=\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k\\
\end{align} on (derivaattojen suhteen) paras
. Tällöin Taylor-polynomi \begin{align}
P_n(x)&=P_n(x;x_0)\\\
&=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+ \\
& \dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\
&=\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k\\
\end{align} on (derivaattojen suhteen) paras  -asteinen polynomiapproksimaatio funktiolle
-asteinen polynomiapproksimaatio funktiolle  pisteen
pisteen  lähellä.
lähellä.
Jos  on
on  kertaa derivoituva pisteessä
kertaa derivoituva pisteessä  , niin Taylor-polynomilla on pisteessä
, niin Taylor-polynomilla on pisteessä  samat derivaatat kuin funktiolla
samat derivaatat kuin funktiolla  , aina (derivaatan) kertalukuun
, aina (derivaatan) kertalukuun  saakka.
saakka.
Syy (tapaus  ): Olkoon
): Olkoon
 jolloin
\begin{align}
P_n'(x)&=c_1+2c_2x+3c_3x^2+\dots +nc_nx^{n-1}, \\
P_n''(x)&=2c_2+3\cdot 2 c_3x\dots +n(n-1)c_nx^{n-2} \\
P_n'''(x)&=3\cdot 2 c_3\dots +n(n-1)(n-2)c_nx^{n-3} \\
\dots && \\
P^{(k)}(x)&=k!c_k + x\text{ termejä} \\
\dots & \\
P^{(n)}(x)&=n!c_n \\
P^{(n+1)}(x)&=0.
\end{align}
jolloin
\begin{align}
P_n'(x)&=c_1+2c_2x+3c_3x^2+\dots +nc_nx^{n-1}, \\
P_n''(x)&=2c_2+3\cdot 2 c_3x\dots +n(n-1)c_nx^{n-2} \\
P_n'''(x)&=3\cdot 2 c_3\dots +n(n-1)(n-2)c_nx^{n-3} \\
\dots && \\
P^{(k)}(x)&=k!c_k + x\text{ termejä} \\
\dots & \\
P^{(n)}(x)&=n!c_n \\
P^{(n+1)}(x)&=0.
\end{align}
Tämän avulla kertoimet voidaan ratkaista yksi kerrallaan:
\begin{align}
c_0= P_n(0)=f(0) &\Rightarrow c_0=f(0) \\
c_1=P_n'(0)=f'(0) &\Rightarrow c_1=f'(0) \\
2c_2=P_n''(0)=f''(0) &\Rightarrow c_2=\frac{1}{2}f''(0) \\
\vdots & \\
k!c_k=P_n^{(k)}(0)=f^{(k)}(0) &\Rightarrow c_k=\frac{1}{k!}f^{(k)}(0). \\
\vdots &\\
n!c_n=P_n^{(n)}(0)=f^{(n)}(0) &\Rightarrow c_k=\frac{1}{n!}f^{(n)}(0).
\end{align} Kertaluvusta  alkaen lisäehtoja ei voi enää asettaa, koska
alkaen lisäehtoja ei voi enää asettaa, koska  .
.
Taylorin kaava
Jos derivaatta  on olemassa ja jatkuva jollakin välillä
on olemassa ja jatkuva jollakin välillä ![I=\, ]x_0-\delta,x_0+\delta[ I=\, ]x_0-\delta,x_0+\delta[](https://mycourses.aalto.fi/filter/tex/pix.php/80a209f739b80f113803ee7e47c63030.gif) , niin
, niin
 ja virhetermille
ja virhetermille  pätee
pätee
 jollakin
jollakin ![c\in [x_0,x]\subset I c\in [x_0,x]\subset I](https://mycourses.aalto.fi/filter/tex/pix.php/a6c59d54e8895e424cf74ad41528b3fe.gif) . Jos on olemassa sellainen vakio
. Jos on olemassa sellainen vakio  (indeksistä
(indeksistä  riippumaton), että
riippumaton), että
 kaikilla
kaikilla  , niin
, niin
 kun
kun  .
.
Todistus sivuutetaan (mathemaattinen induktio tai osittaisintegrointi).
Examples of Maclaurin polynomial approximations: \begin{align} \frac{1}{1-x} &\approx 1+x+x^2+\dots +x^n =\sum_{k=0}^{n}x^k\\ e^x&\approx 1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\dots + \frac{1}{n!}x^n =\sum_{k=0}^{n}\frac{x^k}{k!}\\ \ln (1+x)&\approx x-\frac{1}{2}x^2+\frac{1}{3}x^3-\dots + \frac{(-1)^{n-1}}{n}x^n =\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}x^k\\ \sin x &\approx x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\dots +\frac{(-1)^n}{(2n+1)!}x^{2n+1} =\sum_{k=0}^{n}\frac{(-1)^k}{(2k+1)!}x^{2k+1}\\ \cos x &\approx 1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\dots +\frac{(-1)^n}{(2n)!}x^{2n} =\sum_{k=0}^{n}\frac{(-1)^k}{(2k)!}x^{2k} \end{align}
Esimerkki
Kuinka mones Taylor-polynomi  approksimoi funktiota
approksimoi funktiota  välillä
välillä ![[-\pi,\pi] [-\pi,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/a5d4b5c6dcadd17bce3289ba1891d927.gif) niin hyvin, että virheen itseisarvo on alle
niin hyvin, että virheen itseisarvo on alle  ?
?
Käytetään Taylorin kaavaa funktiolle  pisteen
pisteen  suhteen. Tällöin
suhteen. Tällöin
 riippumatta luvusta
riippumatta luvusta  ja pisteestä
ja pisteestä  . Lisäksi kyseisellä välillä on
. Lisäksi kyseisellä välillä on  . Ehto toteutuu (ainakin silloin) kun
. Ehto toteutuu (ainakin silloin) kun
 Tämä epäyhtälö täytyy ratkaista kokeilemalla luvun
Tämä epäyhtälö täytyy ratkaista kokeilemalla luvun  eri arvoja; ratkaisuksi saadaan
eri arvoja; ratkaisuksi saadaan  .
.
Vaadittu tarkkuus saadaan siis polynomilla  , joka on sinifunktion tapauksessa sama kuin
, joka on sinifunktion tapauksessa sama kuin  .
.
Kuvaajista tms. voi tarkistaa, ettei  riitä vaadittuun tarkkuteen, joten teoreettinen raja on tarkka!
riitä vaadittuun tarkkuteen, joten teoreettinen raja on tarkka!
Taylorin polynomi ja ääriarvot
Jos  , niin myös osa korkeamman kertaluvun derivaatoista voi olla nollia:
, niin myös osa korkeamman kertaluvun derivaatoista voi olla nollia:
 Tällöin funktion
Tällöin funktion  käyttäytyminen pisteen
käyttäytyminen pisteen  lähellä määräytyy (vakiotermi
lähellä määräytyy (vakiotermi  ei vaikuta) Taylor-polynomin johtavasta termistä
ei vaikuta) Taylor-polynomin johtavasta termistä
 .
.
Tämä johtaa seuraavaan tulokseen:
Ääriarvot
Newtonin menetelmä
The first Taylor polynomial  is the same as
the linearization of
is the same as
the linearization of  at the point
at the point  . This can be used
in some simple approximations and numerical methods.
. This can be used
in some simple approximations and numerical methods.
Newtonin menetelmä
Yhtälö  voidaan ratkaista likimääräisesti valitsemalla jokin alkupiste
voidaan ratkaista likimääräisesti valitsemalla jokin alkupiste  (esimerkiksi kuvaajan perusteella) ja määrittelemällä lukujono palautuskaavalla
(esimerkiksi kuvaajan perusteella) ja määrittelemällä lukujono palautuskaavalla
 for
for  Tämä johtaa jonoon
Tämä johtaa jonoon  , jonka termit approksimoivat yleensä funktion
, jonka termit approksimoivat yleensä funktion  nollakohtaa yhä paremmin indeksin
nollakohtaa yhä paremmin indeksin  kasvaessa.
kasvaessa.
Palautuskaava perustuu geometriseen ideaan, jossa funktion nollakohtaa approksimoidaan sen tangenttisuoran nollakohdan avulla. Kyseessä on funktion linearisointi eli 1. asteen Taylor-polynomi edellisen pisteen  suhteen.
suhteen.
Esimerkki
Määritä luvun  likiarvo Newtonin menetelmän avulla.
likiarvo Newtonin menetelmän avulla.
Käytetään Newtonin menetelmää funktiolle  ja alkuarvoa
ja alkuarvoa  . Palautuskaava tulee muotoon
. Palautuskaava tulee muotoon
 josta saadaan
josta saadaan  ,
,  ,
,  jne.
jne.
Kokeilemalla huomataan (esim. Maple), että oikeiden desimaalien lukumäärä suunnilleen kaksinkertaistuu jokaisella askeleella, ja  tuottaa yli 100 oikeaa desimaalia, kunhan välivaiheet lasketaan riittävällä tarkkuudella.
tuottaa yli 100 oikeaa desimaalia, kunhan välivaiheet lasketaan riittävällä tarkkuudella.
Taylor-sarja
Taylor-sarja
Jos Taylorin kaavan virhetermi  lähestyy nollaa, kun
lähestyy nollaa, kun  kasvaa, niin Taylor-polynomin raja-arvona saadaan Taylor-sarja
kasvaa, niin Taylor-polynomin raja-arvona saadaan Taylor-sarja  (= Maclaurin-sarja tapauksessa
(= Maclaurin-sarja tapauksessa  ).
).
Funktion  Taylor-sarja on muotoa
Taylor-sarja on muotoa
 Tämä on esimerkki potenssisarjasta.
Tämä on esimerkki potenssisarjasta.
Taylor-sarja voidaan muodostaa aina, kun funktiolla  on kaikkien kertalukujen derivaatat pisteessä
on kaikkien kertalukujen derivaatat pisteessä  ja nämä sijoitetaan ym. kaavaan.
Tähän liittyy kuitenkin kaksi ongelmaa: 1. Suppeneeko Taylor-sarja kaikilla muuttujan arvoilla
ja nämä sijoitetaan ym. kaavaan.
Tähän liittyy kuitenkin kaksi ongelmaa: 1. Suppeneeko Taylor-sarja kaikilla muuttujan arvoilla  ?
?
Vastaus: Ei aina; esimerkiksi funktion
 Maclaurin-sarja (= geometrinen sarja) suppenee vain arvoilla
Maclaurin-sarja (= geometrinen sarja) suppenee vain arvoilla  , vaikka alkuperäinen funktio on derivoituva pisteissä
, vaikka alkuperäinen funktio on derivoituva pisteissä
 :
:

 ja iteroi (monta kertaa) funktion nollakohdan likiarvon selvittämiseksi.
ja iteroi (monta kertaa) funktion nollakohdan likiarvon selvittämiseksi.
2. Jos sarja suppenee jollakin arvolla  , niin onko sarjan summa sama kuin
, niin onko sarjan summa sama kuin  ? Vastaus: Ei aina; esimerkiksi funktiolle
? Vastaus: Ei aina; esimerkiksi funktiolle
 pätee
pätee  kaikilla
kaikilla  (alkeellinen, mutta teknisesti hieman hankala lasku). Näin ollen
sen Maclaurin-sarja on identtisesti nolla ja suppenee kohti arvoa
(alkeellinen, mutta teknisesti hieman hankala lasku). Näin ollen
sen Maclaurin-sarja on identtisesti nolla ja suppenee kohti arvoa
 vain kohdassa
vain kohdassa  .
.
Johtopäätös: Taylor-sarjoja pitäisi aina tutkia huolellisesti analysoimalla virhetermejä. Käytännössä voidaan kuitenkin usein käyttää tunnettuja sarjakehitelmiä apuna.
Esimerkkejä
\begin{align}
\frac{1}{1-x} &= \sum_{k=0}^{\infty} x^k,\ \ |x|< 1 \\
e^x &= \sum_{k=0}^{\infty} \frac{1}{k!}x^k, \ \ x\in \mathbb{R} \\
\sin x &= \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k+1)!} x^{2k+1}, \ \ x\in \mathbb{R} \\
\cos x &= \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k)!} x^{2k},\ \ x\in \mathbb{R} \\
(1+x)^r &= 1+\sum_{k=1}^{\infty} \frac{r(r-1)(r-2)\dots (r-k+1)}{k!}x^k,
|x|<1
\end{align} Viimeinen on nimeltään binomisarja ja se voidaan muodostaa kaikilla  . Jos
. Jos
 , niin indeksistä
, niin indeksistä
 alkaen kaikki kertoimet ovat nollia, ja alkuosassa
alkaen kaikki kertoimet ovat nollia, ja alkuosassa

Potenssisarja
Määritelmä: Potenssisarja
Potenssisarja on muotoa  Piste
Piste  on sarjan keskus luvut
on sarjan keskus luvut  ovat potenssisarjan kertoimet.
ovat potenssisarjan kertoimet.
Sarja suppenee pisteessä  , jos ym. raja-arvo on olemassa ja äärellinen.
, jos ym. raja-arvo on olemassa ja äärellinen.
Suppenemisen suhteen on vain kolme olennaisesti erilaista tapausta:
Abelin lause.
- Sarja suppenee vain arvolla
 (jolloin siinä esiintyy pelkästään vakio
(jolloin siinä esiintyy pelkästään vakio  )
) - Sarja suppenee kaikilla

- Sarja supppenee jollakin välillä
![]x_0-R,x_0+R[ ]x_0-R,x_0+R[](https://mycourses.aalto.fi/filter/tex/pix.php/2fd864d834cac73e2a4d36123a80ee3e.gif) (ja mahdollisesti yhdessä tai molemmissa päätepisteissä), ja hajaantuu muilla muuttujan
(ja mahdollisesti yhdessä tai molemmissa päätepisteissä), ja hajaantuu muilla muuttujan  arvoilla.
arvoilla.
Luku  on potenssisarjan suppenemissäde. Kahdessa ensimmäisessä tapauksessa merkitään
on potenssisarjan suppenemissäde. Kahdessa ensimmäisessä tapauksessa merkitään  tai
tai  .
.
Esimerkki
Millä muuttujan  arvoilla potenssisarja
arvoilla potenssisarja
 suppenee?
suppenee?
Käytetään suhdetestiä lausekkeelle  . Silloin
. Silloin
 kun
kun  . Suhdetestin perusteella sarja suppenee, kun
. Suhdetestin perusteella sarja suppenee, kun  , ja hajaantuu arvoilla
, ja hajaantuu arvoilla  . Rajatapauksissa
. Rajatapauksissa  sarjan yleinen termi ei lähesty nollaa, joten sarja hajaantuu.
sarjan yleinen termi ei lähesty nollaa, joten sarja hajaantuu.
Tulos: Sarja suppenee arvoilla  , ja hajaantuu muuten.
, ja hajaantuu muuten.
Määritelmä: Summafunktio
Sarjan suppenemisvälillä  voidaan määritellä funktio
voidaan määritellä funktio  asettamalla
\begin{equation}
\label{summafunktio}
f(x) = \sum_{k=0}^{\infty} c_k(x-x_0)^k, \tag{1}
\end{equation} jota kutsutaan potenssisarjan summafunktioksi.
asettamalla
\begin{equation}
\label{summafunktio}
f(x) = \sum_{k=0}^{\infty} c_k(x-x_0)^k, \tag{1}
\end{equation} jota kutsutaan potenssisarjan summafunktioksi.
Summafunktio  on jatkuva ja derivoituva avoimella välillä
on jatkuva ja derivoituva avoimella välillä ![]x_0-R,x_0+R[ ]x_0-R,x_0+R[](https://mycourses.aalto.fi/filter/tex/pix.php/2fd864d834cac73e2a4d36123a80ee3e.gif) . Lisäksi derivaatta
. Lisäksi derivaatta  voidaan laskea derivoimalla potenssisarja termeittäin:
voidaan laskea derivoimalla potenssisarja termeittäin:
 Huom. Vakiotermi
Huom. Vakiotermi  häviää derivoinnissa, joten summaus alkaa kohdasta
häviää derivoinnissa, joten summaus alkaa kohdasta  . Derivoitu sarja suppenee samalla välillä
. Derivoitu sarja suppenee samalla välillä
![x\in \, ]x_0-R,x_0+R[ x\in \, ]x_0-R,x_0+R[](https://mycourses.aalto.fi/filter/tex/pix.php/d78ea0cb1a77dcbd15ccf984e92e4a20.gif) kuin alkuperäinen potenssisarja; tämä voi tuntua hieman yllättävältä kertoimen
kuin alkuperäinen potenssisarja; tämä voi tuntua hieman yllättävältä kertoimen  vuoksi.
vuoksi.
Esimerkki
Määritä potenssisarjan  summafunktio.
summafunktio.
Tämä sarja saadaan derivoimalla termeittäin geometrinen sarja
(kun  ). Näin ollen
\begin{align}
1+2x+3x^2+4x^3+\dots &= D(1+x+x^2+x^3+x^4+\dots ) \\
&= \frac{d}{dx}\left( \frac{1}{1-x}\right) = \frac{1}{(1-x)^2}.
\end{align} Kerrotaan molemmat puolet termillä
). Näin ollen
\begin{align}
1+2x+3x^2+4x^3+\dots &= D(1+x+x^2+x^3+x^4+\dots ) \\
&= \frac{d}{dx}\left( \frac{1}{1-x}\right) = \frac{1}{(1-x)^2}.
\end{align} Kerrotaan molemmat puolet termillä  , jolloin saadaan
, jolloin saadaan
 joka on voimassa arvoilla
joka on voimassa arvoilla  .
.
Tapauksessa ![[a,b]\subset\ ]x_0-R,x_0+R[ [a,b]\subset\ ]x_0-R,x_0+R[](https://mycourses.aalto.fi/filter/tex/pix.php/8d3ffcad3d0765d5d2a862f2664432be.gif) sarjan voi myös integroida termeittäin:
sarjan voi myös integroida termeittäin:
 Usein integroinnin voi ulottaa myös sarjan suppenemisvälin päätepisteeseen saakka, mutta tämä ei pidä paikkaansa yleisesti.
Usein integroinnin voi ulottaa myös sarjan suppenemisvälin päätepisteeseen saakka, mutta tämä ei pidä paikkaansa yleisesti.
Esimerkki
Lasketaan vuorottelevan harmonisen sarjan summa.
Sijoitetaan aluksi  geometrisen sarjan summakaavaan. Näin saadaan
geometrisen sarjan summakaavaan. Näin saadaan
 Integroidaan yhtälön molemmat puolet pisteestä
Integroidaan yhtälön molemmat puolet pisteestä  pisteeseen
pisteeseen  , jolloin saadaan
, jolloin saadaan
 Huom. Integroinnin ulottaminen pisteeseen
Huom. Integroinnin ulottaminen pisteeseen  saakka pitäisi perustella tarkemmin. Integrointiin palataan myöhemmin tällä kurssilla.
saakka pitäisi perustella tarkemmin. Integrointiin palataan myöhemmin tällä kurssilla.
 ',
label : { useMathJax : true }
});
board.update();
i++;
}
function reset(){
i = 0;
document.getElementById("x0").disabled = false;
document.getElementById("x0").value = "";
board.removeObject(points), board.removeObject(segments),
board.removeObject(tangents);
points = [], segments = [], tangents = [];
board.fullUpdate();
}
document.getElementById("iterate").onclick = iterate;
document.getElementById("reset").onclick = reset;
board.fullUpdate();
})();
',
label : { useMathJax : true }
});
board.update();
i++;
}
function reset(){
i = 0;
document.getElementById("x0").disabled = false;
document.getElementById("x0").value = "";
board.removeObject(points), board.removeObject(segments),
board.removeObject(tangents);
points = [], segments = [], tangents = [];
board.fullUpdate();
}
document.getElementById("iterate").onclick = iterate;
document.getElementById("reset").onclick = reset;
board.fullUpdate();
})();
6. Elementary functions
This chapter gives some background to the concept of a function. We also consider some elementary functions from a (possibly) new viewpoint. Many of these should already be familiar from high school mathematics, so in some cases we just list the main properties.
Functions
Definition: Function
A function  is a rule that
determines for each element
is a rule that
determines for each element  exactly one element
exactly one element  .
We write
.
We write  .
.
Definition: Domain and codomain
In the above definition of a function  is the domain (of definition) of the function
is the domain (of definition) of the function  and
and  is called the codomain
of
is called the codomain
of  .
.
Definition: Image of a function
The image of  is the subset
is the subset
![f[A]= \{ f(a) \mid a\in A\} f[A]= \{ f(a) \mid a\in A\}](https://mycourses.aalto.fi/filter/tex/pix.php/c7a396190ef1775b42655b3bae2aeea4.gif) of
of  . An alternative name for image is range.
. An alternative name for image is range.
For example,  ,
,  , has codomain
, has codomain  ,
but its image is
,
but its image is ![f[\mathbb{R} ] =[0,\infty[ f[\mathbb{R} ] =[0,\infty[](https://mycourses.aalto.fi/filter/tex/pix.php/0c14bcce17985fbb3a35d6def4a9a469.gif) .
.
The function in the previous example can also be defined as
 ,
,  , and then the codomain is the same as the image.
In principle, this modification can always be done, but it is not reasonable
in practice.
, and then the codomain is the same as the image.
In principle, this modification can always be done, but it is not reasonable
in practice.
Inverse functions
Observe: A function becomes surjective if all redundant points of the codomain are left out. A function becomes injective if the domain is reduced so that no value of the function is obtained more than once.
Another way of defining these concepts is based on the number of solutions to an equation:
Definition
Definition: Inverse function
If  is bijective, then it has an inverse
is bijective, then it has an inverse
 , which is uniquely determined by the condition
, which is uniquely determined by the condition

The inverse satisfies  for all
for all  and
and
 for all
for all  .
.
The graph of the inverse is the mirror image of the graph of  with respect to the
line
with respect to the
line  : A point
: A point  lies on the graph of
lies on the graph of 




 the point
the point  lies on the
graph of
lies on the
graph of  . The geometric interpretation of
. The geometric interpretation of  is precisely the
reflection with respect to
is precisely the
reflection with respect to  .
.
If  and
and  is strictly monotone, then
the function
is strictly monotone, then
the function ![f\colon A \to f[A] f\colon A \to f[A]](https://mycourses.aalto.fi/filter/tex/pix.php/c6fc43e8a306502af369ccf4e67dfa13.gif) has an inverse.
has an inverse.
If here  is an interval and
is an interval and  is continuous, then also
is continuous, then also  is
is continuous in the set
is
is continuous in the set ![f[A] f[A]](https://mycourses.aalto.fi/filter/tex/pix.php/e81e3f1f3f2f27271e7259b5b1e92b05.gif) .
.
Theorem: Derivative of the inverse
Let ![f\colon \, ]a,b[\, \to\, ]c,d[ f\colon \, ]a,b[\, \to\, ]c,d[](https://mycourses.aalto.fi/filter/tex/pix.php/d743062611593c099de64ea09a96ce0e.gif) be differentiable and bijective, so that it has an inverse
be differentiable and bijective, so that it has an inverse
![f^{-1}\colon \, ]c,d[\, \to\, ]a,b[ f^{-1}\colon \, ]c,d[\, \to\, ]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/12920db7181cead890f182a6b37094a0.gif) . As the graphs
. As the graphs  and
and  are mirror images of each other, it seems geometrically obvious that also
are mirror images of each other, it seems geometrically obvious that also  is differentiable, and we actually have
is differentiable, and we actually have
 if
if  .
.
Transcendental functions
Trigonometric functions
Unit of measurement of an angle = rad: the arclength of the arc on the unit circle, that corresponds to the angle.
The functions
 are defined in terms of the unit circle so that
are defined in terms of the unit circle so that
 ,
, ![x\in [0,2\pi] x\in [0,2\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/45279ec769d88b24314782eea30c7f1e.gif) , is the point on the unit circle corresponding to the
angle
, is the point on the unit circle corresponding to the
angle  , measured counterclockwise from the point
, measured counterclockwise from the point  .
.


Proof: Pythagorean Theorem.
Addition formulas:
Basic properties (from the unit circle!)
Proof: Geometrically, or more easily with vectors and matrices.
Example
It follows that the functions
 and
and  satisfy the
differential equation
satisfy the
differential equation
 that models harmonic oscillation. Here
that models harmonic oscillation. Here  is the time variable
and the constant
is the time variable
and the constant  is the angular frequency of the oscillation.
We will see later that all the solutions of this differential equation
are of the form
is the angular frequency of the oscillation.
We will see later that all the solutions of this differential equation
are of the form
 with
with  constants. They will be uniquely determined if we know
the initial location
constants. They will be uniquely determined if we know
the initial location  and the initial velocity
and the initial velocity  . All solutions
are periodic and their period is
. All solutions
are periodic and their period is  .
.
Arcus functions
The trigonometric functions have inverses if their domain and codomains are chosen in a suitable way.
Here we will only prove the first result (1). By differentiating
both sides of the equation  for
for  :
:



The last row follows also directly from the formula for the derivative of an inverse.
Example
Example
Derive the addition formula for tan, and show that

Solutions: Voluntary exercises. The first can be deduced by looking at
a rectangular triangle with the length of the hypotenuse equal to 1
and one leg of length  .
.
Introduction: Radioactive decay
Let  model the number of radioactive nuclei at time
model the number of radioactive nuclei at time  .
During a short time interval
.
During a short time interval  the number of decaying nuclei is (approximately) directly proportional to
the length of the interval, and also to the number of nuclei at time
the number of decaying nuclei is (approximately) directly proportional to
the length of the interval, and also to the number of nuclei at time  :
:
 The constant
The constant  depends on the substance and is called the decay constant.
From this we obtain
depends on the substance and is called the decay constant.
From this we obtain
 and in the limit as
and in the limit as  we end up with the differential equation
we end up with the differential equation  .
.
Exponential function
Definition: Exponential function
The Exponential function exp:
 This definition (using the series expansion) is based on the conditions
This definition (using the series expansion) is based on the conditions
 and
and  , which imply
that
, which imply
that  for all
for all  ,
so the Maclaurin series is the one above.
,
so the Maclaurin series is the one above.
The connections between different expressions are surprisingly tedious to prove, and we omit the details here. The main steps include the following:
From here on we write  . Properties:
. Properties:
 .
.
Differential equation 
Theorem
Let  be a constant. All solutions
be a constant. All solutions  of the ordinary differenial equation (ODE)
of the ordinary differenial equation (ODE)
 are of the form
are of the form  , where
, where  is a constant. If we know
the value of
is a constant. If we know
the value of  at some point
at some point  , then the constant
, then the constant
 will be uniquely determined.
will be uniquely determined.
Euler's formula
Definition: Complex numbers
Imaginary unit  : a strange creature satisfying
: a strange creature satisfying  . The complex numbers
are of the form
. The complex numbers
are of the form  , where
, where  . We will return to these later.
. We will return to these later.
Theorem: Euler's formula
If we substitute  as a variable in the expontential fuction, and
collect real terms separately, we obtain Euler's formula
as a variable in the expontential fuction, and
collect real terms separately, we obtain Euler's formula

 in the definition of the exponential function and write the series as the sum
of its even (
in the definition of the exponential function and write the series as the sum
of its even ( ) and odd
) and odd  parts. Note that
parts. Note that  and remember the Taylor series of the trigonometric
functions.
and remember the Taylor series of the trigonometric
functions.
As a special case we have Euler's identity  .
It connects the most important numbers
.
It connects the most important numbers  ,
,  ,
,  ,
,  ja
ja  and the
three basic operations sum, multiplication, and power.
and the
three basic operations sum, multiplication, and power.
Logarithms
Hyperbolic functions
Definition: Hyperbolic functions
Hyperbolic sine sinus hyperbolicus  ,
hyperbolic cosine cosinus hyperbolicus
,
hyperbolic cosine cosinus hyperbolicus  and hyperbolic tangent
and hyperbolic tangent
 are defined as
are defined as


![\tanh \colon \mathbb{R}\to \ ]-1,1[, \ \tanh x =\frac{\sinh x}{\cosh x} \tanh \colon \mathbb{R}\to \ ]-1,1[, \ \tanh x =\frac{\sinh x}{\cosh x}](https://mycourses.aalto.fi/filter/tex/pix.php/2ac4198587d98a4f7dd3df05218f66f7.gif)
Properties:  ; all trigonometric have their hyperbolic counterparts,
which follow from the properties
; all trigonometric have their hyperbolic counterparts,
which follow from the properties  ,
,  .
In these formulas, the sign of
.
In these formulas, the sign of  will change, but the other signs remain the same.
will change, but the other signs remain the same.
Hyperbolic inverse functions: the so-called area functions;
area and the shortening ar refer to a certain geometrical area
related to the hyperbola  :
:


 ',
radius : .4,
label : { useMathJax : true, strokeColor : 'black', offset : [0, .5] }
});
var info = board.create('text', [-1.2, -1.25, function() {
return '
',
radius : .4,
label : { useMathJax : true, strokeColor : 'black', offset : [0, .5] }
});
var info = board.create('text', [-1.2, -1.25, function() {
return ' ';
}], {
useMathJax : true,
fixed : true
});
board.fullUpdate();
})();
';
}], {
useMathJax : true,
fixed : true
});
board.fullUpdate();
})();
7. Pinta-ala
Pinta-ala tasossa
Tarkastellaan umpinaisen ja itseään leikkaamattoman tasokäyrän raamien alueiden pinta-alaa. Pinta-alan yleinen käsite on teoreettisesti paljon hankalampi, mistä antaa viitteen luvun lopussa oleva huomautus.
Tasojoukon pinta-ala määritellään palauttamalla se yksinkertaisempien joukkojen pinta-aloihin. Erityisesti täytyy huomata, ettei pinta-alaa voi "laskea", ellei "pinta-alan" käsitettä ole ensin määritelty (vaikka koulumatematiikassa näin usein tehdäänkin).
Lähtökohta
Monikulmio
(Yksinkertainen) monikulmio on tasojoukko, jota rajaa äärellisestä määrästä peräkkäisiä janoja koostuva suljettu käyrä. Vain peräkkäiset janat saavat leikata toisiaan yhteisessä päätepisteessä.
Määritelmä: Monikulmion pinta-ala
Monikulmion pinta-ala määritellään jakamalla se
äärelliseen määrään kolmioita (monikulmion
Lause.
Kolmioiden pinta-alojen summaf ei riipu monikulmion kolmioinnin valinnasta.
Yleinen tapaus
Tasojoukolle  , jota rajaa umpinainen itseään leikkaamaton käyrä, voidaan muodostaa
sisämonikulmioita
, jota rajaa umpinainen itseään leikkaamaton käyrä, voidaan muodostaa
sisämonikulmioita  ja ulkomonikulmioita
ja ulkomonikulmioita
 :
:  .
.
 on pinta-ala, jos jokaista
on pinta-ala, jos jokaista  vastaa sisämonikulmio
vastaa sisämonikulmio  ja ulkomonikulmio
ja ulkomonikulmio  , joiden pinta-alat poikkeavat toisistaan vähemmän kuin
, joiden pinta-alat poikkeavat toisistaan vähemmän kuin  :
:
 Tästä seuraa, että kaikkien lukujen
Tästä seuraa, että kaikkien lukujen  ja kaikkien lukujen
ja kaikkien lukujen  välissä on yksikäsitteinen luku
välissä on yksikäsitteinen luku  , joka on määritelmän mukaan joukon
, joka on määritelmän mukaan joukon  pinta-ala.
pinta-ala.
Yllätys: Se, että joukkoa  rajoittaa umpinainen (itseään leikkaamaton)
käyrä, ei takaa, että joukon pinta-ala on määritelty: Reunakäyrä voi olla niin "mutkitteleva",
että sillä on positiivinen "pinta-ala". Ensimmäisen esimerkin konstruoi [W.F. Osgood, 1903]:
rajoittaa umpinainen (itseään leikkaamaton)
käyrä, ei takaa, että joukon pinta-ala on määritelty: Reunakäyrä voi olla niin "mutkitteleva",
että sillä on positiivinen "pinta-ala". Ensimmäisen esimerkin konstruoi [W.F. Osgood, 1903]:
8. Integral
From sum to integral
Definite integral
Geometric interpretation: Let ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) be such that
be such that  for all
for all
![x\in[a,b] x\in[a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/c7c42309c359c25dfe77f397d5261997.gif) . How can we find the area of the region bounded by the function graph
. How can we find the area of the region bounded by the function graph  , the
x-axis and the two lines
, the
x-axis and the two lines  and
and  ?
?
The answer to this question is given by the definite integral
 Remark. The general definition of the integral does not necessitate the condition
Remark. The general definition of the integral does not necessitate the condition  .
.
Integration of continuous functions
Definition: Partition
Let ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) be continuous. A finite sequence
be continuous. A finite sequence  of real numbers such that
of real numbers such that
 is called a partition of the interval
is called a partition of the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) .
.
Definition: Upper and lower sum
For each partition  we define the related upper sum of the function
we define the related upper sum of the function  as
as
 and the lower sum as
and the lower sum as

If  is a positive function then the upper sum represents the total area of the rectangles circumscribing
the function graph and similarly the lower sum is the total area of the inscribed rectangles.
is a positive function then the upper sum represents the total area of the rectangles circumscribing
the function graph and similarly the lower sum is the total area of the inscribed rectangles.
Properties of partitions
Definition: Integrability
We say that a function ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) is integrable if for every
is integrable if for every  there exists a corresponding partition
there exists a corresponding partition  of
of ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) such that
such that

Definition: Integral
Integrability implies that there exists a unique real number  such that
such that  for every
partition
for every
partition  . This is called the integral of
. This is called the integral of  over the interval
over the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) and denoted by
and denoted by

Remark. This definition of the integral is sometimes referred to as the Darboux integral.
For non-negative functions  this definition of the integral coincides with the idea of making the difference
between the the areas of the circumscribed and the inscribed rectangles arbitrarily small by using ever finer partitions.
this definition of the integral coincides with the idea of making the difference
between the the areas of the circumscribed and the inscribed rectangles arbitrarily small by using ever finer partitions.
Theorem.
A continuous function on a closed interval is integrable.
Here we will only provide the proof for continuous functions with bounded derivatives.
Suppose that ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) is a continuous function and that there exists a constant
is a continuous function and that there exists a constant  such that
such that
 for all
for all ![x\in]a,b[ x\in]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/446e008dffdc84c23608a41270477f2f.gif) . Let
. Let  and define
and define  to be an equally spaced partition of
to be an equally spaced partition of ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) such that
such that
 Let
Let  and
and  for some suitable points
for some suitable points ![y_{k},z_{k}\in[x_{k-1},x_{k}] y_{k},z_{k}\in[x_{k-1},x_{k}]](https://mycourses.aalto.fi/filter/tex/pix.php/b0cc09fba8e4e83e7252a84f0c0d25e5.gif) . The mean value theorem
then states that
. The mean value theorem
then states that
 and thus
and thus

Definition: Riemann integral
Suppose that ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) is a continuous function and let
is a continuous function and let
 be a partition of
be a partition of ![\left[a,b\right] \left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/22be842f9527b4b0ef3b7085b5486b7b.gif) and
and
 be a sequence of real numbers such that
be a sequence of real numbers such that
![z_{k}\in[x_{k-1},x_{k}] z_{k}\in[x_{k-1},x_{k}]](https://mycourses.aalto.fi/filter/tex/pix.php/6699d41c4ee1c2de849bc6a2162fd4e7.gif) for all
for all  . The partial sums
. The partial sums
 are called the Riemann sums of
are called the Riemann sums of  . Suppose further that the partitions are
such that
. Suppose further that the partitions are
such that  as
as  .
The integral of
.
The integral of  can then be defined as the limit
can then be defined as the limit
 This definition of the integral is called the Riemann integral.
This definition of the integral is called the Riemann integral.
Remark. This definition of the integral turns out to be equivalent to that of the Darboux integral i.e. a function is Riemann-integrable if and only if it is Darboux-integrable and the values of the two integrals are always equal.
Example
Find the integral of  over the interval
over the interval ![[0,1] [0,1]](https://mycourses.aalto.fi/filter/tex/pix.php/ccfcd347d0bf65dc77afe01a3306a96b.gif) using Riemann sums.
using Riemann sums.
Let  . Then
. Then  ,
,  and
and  for all
for all
 . Thus the sequence
. Thus the sequence  is a proper
partition of
is a proper
partition of ![\left[0,1\right] \left[0,1\right]](https://mycourses.aalto.fi/filter/tex/pix.php/4f27db35c23e1b587a92f6ba055a4b94.gif) . This partition has the pleasant property hat
. This partition has the pleasant property hat
 is a constant. Estimating the Riemann sums we now find that
is a constant. Estimating the Riemann sums we now find that

 as
as  and hence
and hence

This is of course the area of the triangular region bounded by the line  ,
the
,
the  -axis and the lines
-axis and the lines  and
and  .
.
Remark. Any interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) can be partitioned into equally spaced subintervals by setting
can be partitioned into equally spaced subintervals by setting
 and
and  .
.
Conventions
Piecewise-defined functions
Definition: Piecewise continuity
A function ![f\colon\left[a,b\right]\to\mathbb{R} f\colon\left[a,b\right]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/651a926e83a81b2331659e5bec837922.gif) is called piecewise continuous
if it is continuous except at a finite number of points
is called piecewise continuous
if it is continuous except at a finite number of points
 and the one-sided limits of the function are defined and bounded on each of these
points. It follows that the restriction of
and the one-sided limits of the function are defined and bounded on each of these
points. It follows that the restriction of  on each subinterval
on each subinterval
![\left[c_{k-1},c_{k}\right] \left[c_{k-1},c_{k}\right]](https://mycourses.aalto.fi/filter/tex/pix.php/4c8251634c3e4dcef42dea1404161757.gif) is continuous if the one-sided limits are taken to
be the values of the function at the end points of the subinterval.
is continuous if the one-sided limits are taken to
be the values of the function at the end points of the subinterval.
Definition: Piecewise integration
Let ![f\colon\left[a,b\right] f\colon\left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/9f37a3c940314dccb310e7db856fb524.gif) be a piecewise continuous function. Then
be a piecewise continuous function. Then
 where
where  and
and  is thought as a
continuous function on each subinterval
is thought as a
continuous function on each subinterval ![\left[c_{k-1},c_{k}\right] \left[c_{k-1},c_{k}\right]](https://mycourses.aalto.fi/filter/tex/pix.php/4c8251634c3e4dcef42dea1404161757.gif) . Usually
functions which are continuous yet piecewise defined are also integrated using the
same idea.
. Usually
functions which are continuous yet piecewise defined are also integrated using the
same idea.
Important properties
Properties
Suppose that ![f,g\colon\left[a,b\right]\to\mathbb{R} f,g\colon\left[a,b\right]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/f01d397fa4a741a5373783b544f03897.gif) are piecewise continuous
functions. The integral has the following properties
are piecewise continuous
functions. The integral has the following properties
Fundamental theorem of calculus
Theorem: Mean value theorem
Let ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) be a continuous function. Then there exists
be a continuous function. Then there exists  such that
such that
 This is the mean value of
This is the mean value of  on the interval
on the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) and we denote it with
and we denote it with  .
.
Antiderivative
If  on some open interval then
on some open interval then  is the antiderivative
(or the primitive function) of
is the antiderivative
(or the primitive function) of  . The fundamental theorem of calculus
guarantees that for every continuous function
. The fundamental theorem of calculus
guarantees that for every continuous function  there exists an antiderivative
there exists an antiderivative
 The antiderivative is not necessarily expressible as a combination of elementary
functions even if
The antiderivative is not necessarily expressible as a combination of elementary
functions even if  were an elementary function, e.g.
were an elementary function, e.g.  .
Such primitives are called nonelementary antiderivatives.
.
Such primitives are called nonelementary antiderivatives.
Suppose that  for all
for all  . Then the derivative of
. Then the derivative of  is identically zero and thus the difference is a constant.
is identically zero and thus the difference is a constant.
(Second) Fundamental theorem of calculus
Let ![f\colon\left[a,b\right]\to\mathbb{R} f\colon\left[a,b\right]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/651a926e83a81b2331659e5bec837922.gif) be a continuous function and
be a continuous function and  an antiderivative of
an antiderivative of  , then
, then

Integrals of elementary functions
Constant Functions
Given the constant function  . The integral
. The integral  has to be determined now.
has to be determined now.
Solution by finding a antiderivative
From the previous chapter it is known that  gives
gives  . This means that
. This means that  is an antiderivative for
is an antiderivative for  . So the following applies
. So the following applies ![\int\limits_a^b c \, \mathrm{d}x = [c \cdot x]_{x=a}^{x=b} = c\cdot b - c \cdot a = c \cdot (b-a). \int\limits_a^b c \, \mathrm{d}x = [c \cdot x]_{x=a}^{x=b} = c\cdot b - c \cdot a = c \cdot (b-a).](https://mycourses.aalto.fi/filter/tex/pix.php/8665eaa9c4f246caaa2ed563cb0a03e8.gif)
Remark: Of course, a function  would also be an antiderivative of
would also be an antiderivative of  , since the constant
, since the constant  is omitted in the derivation. For sake of simplicity
is omitted in the derivation. For sake of simplicity  can be used, since
can be used, since  can be chosen as
can be chosen as  for definite integrals.
for definite integrals.
Solution by geometry
The area under the constant function forms a rectangle with height  and length
and length  . Thus the area is
. Thus the area is  and this corresponds to the solution of the integral. Illustrate this remark by a sketch.
and this corresponds to the solution of the integral. Illustrate this remark by a sketch.
Linear functions
Given is the linear function  . We are looking for the integral
. We are looking for the integral  .
.
Solve by finding a antiderivative
The antiderivative of a linear function is in any case a quadratic function, since  . The derivative of a quadratic function results in a linear function. Here, it is important to consider the leading factor as in
. The derivative of a quadratic function results in a linear function. Here, it is important to consider the leading factor as in  Thus the result is
Thus the result is ![\int\limits_a^b mx \mathrm{d}x = \left[\frac{m}{2}x^2 \right]_{x=a}^{x=b}= \frac{m}{2}b^2 - \frac{m}{2}a^2. \int\limits_a^b mx \mathrm{d}x = \left[\frac{m}{2}x^2 \right]_{x=a}^{x=b}= \frac{m}{2}b^2 - \frac{m}{2}a^2.](https://mycourses.aalto.fi/filter/tex/pix.php/b5241a45e0cf510936549697bfb8ec04.gif)
Solving by geometry
The integral  can be seen geometrically, as subtracting the triangle with the edges
can be seen geometrically, as subtracting the triangle with the edges  ,
,  and
and  from the triangle with the edges
from the triangle with the edges  ,
,  and
and  . Since the area of a triangle ist given by
. Since the area of a triangle ist given by  , the area of the first triangle
, the area of the first triangle  and that of the second triangle is analogous
and that of the second triangle is analogous  . For the integral the result is
. For the integral the result is  . This is consistent with the integral calculated using the antiderivative. Illustrate this remark by a sketch.
. This is consistent with the integral calculated using the antiderivative. Illustrate this remark by a sketch.
Power functions
In constant and linear functions we have already seen that the exponent of a function decreases by one when it is derived. So it has to get bigger when integrating.
The following applies:  It follows that the antiderivative for
It follows that the antiderivative for  must have the exponent
must have the exponent  ,
,  By multiplying the last equation with
By multiplying the last equation with  we get
we get  Finally the antiderivative is
Finally the antiderivative is  .
.
Examples
The formula ![\int x^n\, \mathrm dx = [\frac{1}{n+1} x^{n+1}] \int x^n\, \mathrm dx = [\frac{1}{n+1} x^{n+1}]](https://mycourses.aalto.fi/filter/tex/pix.php/222a5eca783899397010e410d9be1ac6.gif) is also valid, if the exponent of the function is a real number and not equal
is also valid, if the exponent of the function is a real number and not equal  .
.
Examples
Natural Exponential function
The natural exponential function  is one of the easiest function to differentiate and integrate.
Since the derivation of
is one of the easiest function to differentiate and integrate.
Since the derivation of  results in
results in  , it follows
, it follows 
Example 1
Determine the value of the integral  .
.
Example 2
Determine the value of the integral  . Using the same considerations as above we get
. Using the same considerations as above we get  Important is here, that we have to use the factor
Important is here, that we have to use the factor  .
.
Natural Logarithm
The derivative of the natural logarithmic function is  for
for  . It even applies
. It even applies  to
to  . These results together result in for the antiderivative of
. These results together result in for the antiderivative of 

An antiderivative can be specified for the natural logarithm: 
Trigonometric function
The antiderivatives of  and
and  also result logically if you derive "backwards". We have
also result logically if you derive "backwards". We have
 since
since  Furthermore we know
Furthermore we know  since
since  applies.
applies.
Example 1
Which area is covered by the sine on the interval ![[0,\pi] [0,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/a79560c6f70853be01bb23f7539e168c.gif) and the
and the  -axis?
To determination the area we simply have to evaluate the integral
-axis?
To determination the area we simply have to evaluate the integral
 That means
That means ![\int_0^{\pi} \sin(\tau) \, \mathrm{d}\tau = \left[-\cos(\tau)\right]_{\tau=0}^{\tau=\pi} =
-\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 2. \int_0^{\pi} \sin(\tau) \, \mathrm{d}\tau = \left[-\cos(\tau)\right]_{\tau=0}^{\tau=\pi} =
-\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 2.](https://mycourses.aalto.fi/filter/tex/pix.php/ed010b1da078996da59e937f6091bf5f.gif) Again make a sketch for this example.
Again make a sketch for this example.
Example 2
How can the integral  be expressed analytically?
be expressed analytically?
To determine the integral we use the antiderivative of the cosine:  . However, the inner derivativ has to be considered in the
given function and thus we get
. However, the inner derivativ has to be considered in the
given function and thus we get 
Example 1
Solution. The antiderivative of  is
is  so we have that
so we have that
 The antiderivative of
The antiderivative of  is
is  and thus
and thus

Example 2
Solution. The antiderivative might look something like  , where we can find the factor
, where we can find the factor  through differentiation:
through differentiation:
 hence if
hence if  we get the correct antiderivative. Thus
we get the correct antiderivative. Thus
 This integral can also be solved using integration by substitution; more on this method later.
This integral can also be solved using integration by substitution; more on this method later.
Geometric applications
Area of a plane region
Suppose that  and
and  are piecewise continuous functions. The area of a region bounded by the graphs
are piecewise continuous functions. The area of a region bounded by the graphs  ,
,  and the vertical lines
and the vertical lines  and
and  is given by the integral
is given by the integral

Especially if  is a non-negative function on the interval
is a non-negative function on the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) and
and  for all
for all  then the integral
then the integral
 is the area of the region bounded by the graph
is the area of the region bounded by the graph  , the
, the  -axis and the vertical lines
-axis and the vertical lines  and
and  .
.
Arc length
Surface of revolution
The area of a surface generated by rotating the graph  around the
around the  -axis on the interval
-axis on the interval ![\left[a,b\right] \left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/22be842f9527b4b0ef3b7085b5486b7b.gif) is given by
is given by
 Heuristic reasoning: An area element of the surface is approximately
Heuristic reasoning: An area element of the surface is approximately

Solid of revolution
Suppose that the cross-sectional area of a solid is given by the function  when
when ![x\in\left[a,b\right] x\in\left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/2f48f5b87131a8927f62cdab351ef9f5.gif) . Then the volume of the solid is given by the integral
. Then the volume of the solid is given by the integral
 If the graph
If the graph  is rotated around the
is rotated around the  -axis between the lines
-axis between the lines  and
and  the volume of the generated figure (the solid of revolution) is
the volume of the generated figure (the solid of revolution) is
 This follows from the fact that the cross-sectional area of the figure at
This follows from the fact that the cross-sectional area of the figure at  is a circle with radius
is a circle with radius  i.e.
i.e.  .
.
More generally: Let  and suppose that the region bounded by
and suppose that the region bounded by  and
and  and the lines
and the lines  and
and  is rotated around the
is rotated around the  -axis. The volume of this solid of revolution is
-axis. The volume of this solid of revolution is

Improper integral
Definition: Improper integral
One limitation of the improper integration is that the limit must be taken with respect to one endpoint at a time.
Example
 Provided that both of the integrals on the right-hand side converge. If either of the two is divergent then so is the integral.
Provided that both of the integrals on the right-hand side converge. If either of the two is divergent then so is the integral.
Definition
Let  be a piecewise continuous function. Then
be a piecewise continuous function. Then
 provided that the limit exists and is finite. We say that the improper integral of
provided that the limit exists and is finite. We say that the improper integral of  converges over
converges over  .
.
Likewise for ![f\colon\left]-\infty,b\right]\to\mathbb{R} f\colon\left]-\infty,b\right]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/cc67a3edd5c24ca829bb065e2a3d65b4.gif) we define
we define
 provided that the limit exists and is finite.
provided that the limit exists and is finite.
Example
Solution. Notice that
 as
as  . Thus the improper integral converges and
. Thus the improper integral converges and

Definition
Let  be a piecewise continuous function. Then
be a piecewise continuous function. Then
 if both of the two integrals on the right-hand side converge.
if both of the two integrals on the right-hand side converge.
However, this doesn't apply in general. For example, let  . Note that even though
. Note that even though
 for all
for all  the improper integral
the improper integral
 does not converge.
does not converge.
Improper integrals of the 2nd kind are handled in a similar way using limits. As there are many different (but essentially rather similar) cases, we leave the matter to one example only.
Comparison test
Example 2
Notice that
 and that the integral
and that the integral
 converges. Thus by the comparison test the integral
converges. Thus by the comparison test the integral
 also converges and its value is less than or equal to
also converges and its value is less than or equal to  .
.
Example 3
Likewise
 and because
and because  converges so does
converges so does
 and its value is less than or equal to
and its value is less than or equal to  .
.
Note. The choice of the dominating function depends on both the original function and the interval of integration.
Example 4
Determine whether the integral
 converges or diverges.
converges or diverges.
Solution. Notice that  for all
for all  and therefore
and therefore
 Now, because the integral
Now, because the integral  diverges then by the comparison test so does the original integral.
diverges then by the comparison test so does the original integral.
Integration techniques
Logarithmic integration
Given a quotient of differentiable functions, we know to apply the quotient rule. However, this is not so easy with integration. Here only for a few special cases we will state rules in this chapter.
Logarithmic integration As we already know the derivative of  , i.e. the natural logarithm to the base
, i.e. the natural logarithm to the base  , equal to
, equal to  . According to the chain rule the derivative of differentiable function with positive function values is
. According to the chain rule the derivative of differentiable function with positive function values is  . This means that for a quotient of functions where the numerator is the derivative of the denominator yields the rule: \begin{equation} \int \frac{f'(x)}{f(x)}\, \mathrm{d} x= \ln \left(|f(x)|\right) +c,\,c\in\mathbb{R}.\end{equation} Using the absolute value of the function is important, since the logarithm is defined on
. This means that for a quotient of functions where the numerator is the derivative of the denominator yields the rule: \begin{equation} \int \frac{f'(x)}{f(x)}\, \mathrm{d} x= \ln \left(|f(x)|\right) +c,\,c\in\mathbb{R}.\end{equation} Using the absolute value of the function is important, since the logarithm is defined on  .
.
Examples
Integration of rational functions - partial fraction decomposition
The logarithmic integration works well in special cases of broken rational functions where the counter is a multiple of the derivation of the denominator. However, other cases can sometimes be traced back to this. This method is called partial fractional decomposition, which represents rational functions as the sum of proper rational functions.
Example 1
The function  cannot be integrated at first glance. However, the denominator
cannot be integrated at first glance. However, the denominator  can be written as
can be written as  and the function can finally reads as
and the function can finally reads as  by partial fraction decomposition. This expression can be integrated, as demonstrated now: \begin{eqnarray} \int \dfrac{1}{1-x^2} \,\mathrm dx &= & \int \dfrac{\frac{1}{2}}{1+x} + \dfrac{\frac{1}{2}}{1-x}\, \mathrm dx \\ & =& \frac{1}{2} \int \dfrac{1}{1+x}\, \mathrm dx - \frac{1}{2} \int \dfrac{-1}{1-x}\, \mathrm dx\\ & = &\frac{1}{2} \ln|1+x| +c_1 - \frac{1}{2} \ln|1-x| +c_2\\ &= &\frac{1}{2} \ln \left|\dfrac{1+x}{1-x}\right|+c,\,c\in\mathbb{R}. \end{eqnarray} This procedure is now described in more detail for some special cases.
by partial fraction decomposition. This expression can be integrated, as demonstrated now: \begin{eqnarray} \int \dfrac{1}{1-x^2} \,\mathrm dx &= & \int \dfrac{\frac{1}{2}}{1+x} + \dfrac{\frac{1}{2}}{1-x}\, \mathrm dx \\ & =& \frac{1}{2} \int \dfrac{1}{1+x}\, \mathrm dx - \frac{1}{2} \int \dfrac{-1}{1-x}\, \mathrm dx\\ & = &\frac{1}{2} \ln|1+x| +c_1 - \frac{1}{2} \ln|1-x| +c_2\\ &= &\frac{1}{2} \ln \left|\dfrac{1+x}{1-x}\right|+c,\,c\in\mathbb{R}. \end{eqnarray} This procedure is now described in more detail for some special cases.
Case 1:  with
with  . In this case,
. In this case,  has the representation
has the representation  and can be transformed to
and can be transformed to  By multiplying with
By multiplying with  it yields ot
it yields ot 
 and
and  are now obtained by the method of equating the coefficients.
are now obtained by the method of equating the coefficients.
Example 2
Determe the partial fraction decomposition of  .
.
Start with the equation  to get the parameters
to get the parameters  and
and  . Multiplication by
. Multiplication by  leads to
leads to  Now we get the system of linear equations
Now we get the system of linear equations
\begin{eqnarray}A+B & = & 2 \\ 5A - 4 B &=& 3\end{eqnarray} with the solution  and
and  . The representation with proper rational functions is
. The representation with proper rational functions is  The integral of the type
The integral of the type  is no longer mystic.
is no longer mystic.
With the help of partial fraction decomposition, this integral can now be calculated in the following manner \begin{eqnarray}\int \frac{ax+b}{(x-\lambda_1)(x-\lambda_2)}\mathrm{d} x &=& \int\frac{A}{(x-\lambda_1)}+\frac{B}{(x-\lambda_2)}\mathrm{d} x \\ &=&A\int\frac{1}{(x-\lambda_1)}\mathrm{d} x +B\int\frac{1}{(x-\lambda_2)}\mathrm{d} x \\ & = & A\ln(|x-\lambda_1|) + B\ln(|x-\lambda_2|).\end{eqnarray}
Example 3
Determine the antiderivative for  , i.e.
, i.e. 
From the above example we already know: 
Using the idea explained above immediately follow:  So is the result
So is the result 
In this case  has the representation
has the representation  and the ansatz
and the ansatz  is used.
is used.
By multiplying the equation with  we get
we get  Again equating the coefficients leads us to a system of linear equations in
Again equating the coefficients leads us to a system of linear equations in  and
and 
In this case  has the representation
has the representation  and the representation can not be simplified.
and the representation can not be simplified.
Only the special case  is now considered.
is now considered.
Integration by Parts
The derivative of a product of two continuously differentiable functions  and
and  is
is 
This leads us to the following theorem:
Theorem: Integration by Parts
Let and
and  be continuously differentiable functions on the interval
be continuously differentiable functions on the interval ![\left[a,b\right] \left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/22be842f9527b4b0ef3b7085b5486b7b.gif) . Then
. Then
 Likewise for the indefinite integral it holds that
Likewise for the indefinite integral it holds that

It follows from the product rule that
 or rearranging the terms
or rearranging the terms
 Integrating both sides of the equation with respect to
Integrating both sides of the equation with respect to  and ignoring the constant of integration now yields
and ignoring the constant of integration now yields

Example
Solution. Set  and
and  . Then
. Then  and
and  and the integration by parts gives
and the integration by parts gives


Notice that had we chosen  and
and  the other way around this would have led to an even more complicated integral.
the other way around this would have led to an even more complicated integral.
Integration by Substitution
Example 1
Find the value of the integral  .
.
Solution. Making the substitution  when
when  we have
we have  . Solving the limits from the inverse formula i.e.
. Solving the limits from the inverse formula i.e.  we find that
we find that  and
and  . Hence
. Hence

Here the latter integral was solved applying integration by parts in the previous example.
Example 2
![L(f)=' + rsums[1].Value().toFixed(3) + ' L(f)=' + rsums[1].Value().toFixed(3) + '](https://mycourses.aalto.fi/filter/tex/pix.php/7cca90fbd11588571c4518f7bebf98c8.gif) '; }
],{
useMathJax : true,
fontSize : 14,
fixed : true
}));
b1.fullUpdate();
b2.fullUpdate();
};
plotButton.click();
})();
',
label : { useMathJax : true, offset : [0, 30] }
});
board.create('integral', [[0.2, 1.4], graph], { fillColor : 'blue', curveRight : { visible : false }, curveLeft : { visible : false },
withLabel : false,
baseLeft : { visible : true, showinfobox : false, size : 1, strokeColor : 'black', withLabel : true, name : '
'; }
],{
useMathJax : true,
fontSize : 14,
fixed : true
}));
b1.fullUpdate();
b2.fullUpdate();
};
plotButton.click();
})();
',
label : { useMathJax : true, offset : [0, 30] }
});
board.create('integral', [[0.2, 1.4], graph], { fillColor : 'blue', curveRight : { visible : false }, curveLeft : { visible : false },
withLabel : false,
baseLeft : { visible : true, showinfobox : false, size : 1, strokeColor : 'black', withLabel : true, name : ' ', label : { useMathJax : true, offset : [0, -1] }},
baseRight : { visible : true, showinfobox : false, size : 1, strokeColor : 'black', withLabel : true, name : '
', label : { useMathJax : true, offset : [0, -1] }},
baseRight : { visible : true, showinfobox : false, size : 1, strokeColor : 'black', withLabel : true, name : ' ', label : { useMathJax : true, offset : [0, -1] }}
} );
board.fullUpdate();
})();
', label : { useMathJax : true, offset : [0, -1] }}
} );
board.fullUpdate();
})();
9. Differentiaaliyhtälöt
Johdanto
Differentiaaliyhtälö on yhtälö, joka sisältää tuntemattoman funktion, esimerkiksi  , ja sen derivaattoja
, ja sen derivaattoja  . Tässä tuntematon funktio on yhden muuttujan funktio, jolloin puhutaan tavallisista differentiaaliyhtälöistä (ordinary differential equation ODE) tai lyhyesti vain differentiaaliyhtälöistä (DY). Jos tuntematon funktio riippuu useammista muuttujista, niin kyseessä on osittaisdifferentiaaliyhtälö (partial differential equation PDE), mutta niitä ei käsitellä tällä kurssilla.
. Tässä tuntematon funktio on yhden muuttujan funktio, jolloin puhutaan tavallisista differentiaaliyhtälöistä (ordinary differential equation ODE) tai lyhyesti vain differentiaaliyhtälöistä (DY). Jos tuntematon funktio riippuu useammista muuttujista, niin kyseessä on osittaisdifferentiaaliyhtälö (partial differential equation PDE), mutta niitä ei käsitellä tällä kurssilla.
Radioaktiivinen hajoaminen on tyyppillinen ilmiö, joka johtaa differentiaaliyhtälöön. Jos  on radiaktiivisten ydinten lukumäärä ajan hetkellä
on radiaktiivisten ydinten lukumäärä ajan hetkellä  , niin lyhyellä aikavälillä
, niin lyhyellä aikavälillä  ydinten lukumäärän muutos on suunnilleen
ydinten lukumäärän muutos on suunnilleen  , jossa
, jossa  on aineesta riippuva positiivinen vakio (hajoamisvakio). Approksimaatio paranee, kun
on aineesta riippuva positiivinen vakio (hajoamisvakio). Approksimaatio paranee, kun  , joten
, joten  . Näin ollen differentiaaliyhtälö
. Näin ollen differentiaaliyhtälö  on radioaktiivisen hajoamisen matemaattinen malli. Todellisuudessa ydinten lukumäärä
on radioaktiivisen hajoamisen matemaattinen malli. Todellisuudessa ydinten lukumäärä  on kokonaisluku, joka pienenee hyppäyksittäin, eikä se voi olla derivoituva (tai oikeastaan derivaatta on enimmäkseen pelkkää nollaa!). Näin ollen malli kuvaa jonkin idealisoidun version
on kokonaisluku, joka pienenee hyppäyksittäin, eikä se voi olla derivoituva (tai oikeastaan derivaatta on enimmäkseen pelkkää nollaa!). Näin ollen malli kuvaa jonkin idealisoidun version  käyttäytymistä. Tämä ilmiö toistuu useissa matemaattisissa malleissa.
käyttäytymistä. Tämä ilmiö toistuu useissa matemaattisissa malleissa.
Kertaluku
Differentiaaliyhtälön ratkaisu
Kertalukua n oleva DY on yleisesti muotoa
DY:n ratkaisu on sellainen n kertaa derivoituva funktio  , joka toteuttaa yhtälön kaikilla
, joka toteuttaa yhtälön kaikilla  , kun
, kun  on jokin reaaliakselin avoin väli.
on jokin reaaliakselin avoin väli.
Ratkaisut eivät yleensä ole yksikäsitteisiä, vaan niitä on äärettömän monta. Tarkastellaan esimerkiksi differentiaaliyhtälöä  Tämän DY:n ratkaisuja ovat mm.
Tämän DY:n ratkaisuja ovat mm.
Tässä  ,
,  ja
ja  ovat yksittäisratkaisuja. DY:n yleinen ratkaisu on muotoa
ovat yksittäisratkaisuja. DY:n yleinen ratkaisu on muotoa  . Yleisestä ratkaisusta saadaan yksittäisratkaisuja kiinnittämällä parametrille
. Yleisestä ratkaisusta saadaan yksittäisratkaisuja kiinnittämällä parametrille  jokin arvo. Ratkaisuja, joita ei saada tällä tavalla yleisestä ratkaisuta, kutsutaan DY:n erikoisratkaisuiksi.
jokin arvo. Ratkaisuja, joita ei saada tällä tavalla yleisestä ratkaisuta, kutsutaan DY:n erikoisratkaisuiksi.
Kaikilla differentiaaliyhtälöillä ei ole lainkaan ratkaisuja. Esimerkiksi 1. kertaluvun DY:llä  ei ole lainkaan ratkaisuja. Jos 1. kertaluvun DY voidaan kirjoittaa normaalimuodossa
ei ole lainkaan ratkaisuja. Jos 1. kertaluvun DY voidaan kirjoittaa normaalimuodossa  , jossa
, jossa  on jatkuva kahden muuttujan funktio, niin ratkaisuja on olemassa.
on jatkuva kahden muuttujan funktio, niin ratkaisuja on olemassa.
Alkuehdot
Yleisessä ratkaisussa esiintyvät vakiot kiinnittyvät yleensä, jos ratkaisulta vaaditaan joitakin lisäehtoja. Voimme esimerkiksi vaatia, että ratkaisu saa arvon  kohdassa
kohdassa  asettamalla alkuehto
asettamalla alkuehto  Ensimmäisen kertaluvun differentiaaliyhtälöiden kohdalla yksi alkuehto riittää (yleensä) takaamaan ratkaisun yksikäsitteisyyden. Toisen kertaluvun DY:iden kohdalla tarvitaan kaksi ehtoa, jos halutaan saada yksikäsitteinen ratkaisu. Tällöin alkuehdot tulevat muotoon
Ensimmäisen kertaluvun differentiaaliyhtälöiden kohdalla yksi alkuehto riittää (yleensä) takaamaan ratkaisun yksikäsitteisyyden. Toisen kertaluvun DY:iden kohdalla tarvitaan kaksi ehtoa, jos halutaan saada yksikäsitteinen ratkaisu. Tällöin alkuehdot tulevat muotoon
Huom: Reunaehtojen  ,
,  tapauksessa tilanne on hankalampi.
tapauksessa tilanne on hankalampi.
Yleisen kertalukua n olevan differentiaaliyhtälön tapauksessa tarvitaan n lisäehtoa, jotta ratkaisusta tulee yksikäsitteinen. Differentiaaliyhtälöä yhdessä alkuehtojen kanssa kutsutaan alkuarvotehtäväksi.
Esimerkki 1.
Aikaisemmin todettiin, että differentiaaliyhtälön  yleinen ratkaisu on muotoa
yleinen ratkaisu on muotoa  Näin ollen alkuarvotehtävän
Näin ollen alkuarvotehtävän
Kokeile! Yllä on esitetty joitakin ratkaisuja differentiaaliyyhtälölle
 Tutki, miten alkuehdon muuttaminen vaikuttaa ratkaisuun (siirrä alkuehtopistettä hiirellä). Saatko eri ratkaisukäyrät (ratkaisujen kuvaajat) leikkaamaan toisiaan?
Tutki, miten alkuehdon muuttaminen vaikuttaa ratkaisuun (siirrä alkuehtopistettä hiirellä). Saatko eri ratkaisukäyrät (ratkaisujen kuvaajat) leikkaamaan toisiaan?
Suuntakenttä
Differentiaaliyhtälö  voidaan tulkita myös geometrisesti: jos ratkaisukäyrä (eli ratkaisun kuvaaja) kulkee tason pisteen
voidaan tulkita myös geometrisesti: jos ratkaisukäyrä (eli ratkaisun kuvaaja) kulkee tason pisteen  kautta, niin ratkaisulle pätee
kautta, niin ratkaisulle pätee  , t.s. ratkaisukäyrän tangentin kulmakerroin voidaan määrittää ilman varsinaista ratkaisua
, t.s. ratkaisukäyrän tangentin kulmakerroin voidaan määrittää ilman varsinaista ratkaisua  . Differentiaaliyhtälön suuntakenttä on vektoreiden
. Differentiaaliyhtälön suuntakenttä on vektoreiden  muodostama kenttä, kun niitä piirretään sopiviin hilapisteisiin
muodostama kenttä, kun niitä piirretään sopiviin hilapisteisiin  . Suuntakentästä voidaan usein päätellä ratkaisujen kuvaajien muoto ainakin kvalitatiivisesti..
. Suuntakentästä voidaan usein päätellä ratkaisujen kuvaajien muoto ainakin kvalitatiivisesti..
Ensimmäisen kertaluvun differentiaaliyhtälö
Differentiaaliyhtälöiden teorian suurin vaikeus on siinä, ettei ole olemassa mitään yleispätevää ratkaisumenetelmää, joka toimii kaikissa tai edes yleisemmissä tapauksissa. Monille varsin yksinkertaisillekaan yhtälöille ei ole esimerkiksi mitään ratkaisukaavaa, ja tilanne vaikeutuu entisestään kertaluvun kasvaessa. Tämän vuoksi seuraavassa käsitellään muutamia sellaisia differentiaaliyhtälöitä, jotka voidaan ratkaista ("integroimalla"). Hankalammissa tapauksissa on joskus hyötyä pelkästään siitä, että tiedetään ratkaisun olemassaolo tai yksikäsitteisyys tietyillä alkuehdoilla.
Lineaarinen 1. kertaluvun DY
Muotoa
olevaa DY:ä kutsutaan lineaariseksi differentiaaliyhtälöksi. Vasemman puolen lauseke on lineaarikombinaatio tuntemattomasta funktiosta ja se derivativaatoista, joiden kertoimina ovat funktiot  . Ensimmäisen kertaluvun lineaarinen DY on siis muotoa
. Ensimmäisen kertaluvun lineaarinen DY on siis muotoa
Jos  kaikilla
kaikilla  , niin yhtälö on homogeeninen. Muuten yhtälö on epähomogeeninen.
, niin yhtälö on homogeeninen. Muuten yhtälö on epähomogeeninen.
Lause 1.
Tarkastellan normaalimuotoista differentiaaliyhtälöä
Jos funktiot  ja
ja  ovat jatkuvia välillä
ovat jatkuvia välillä  , joka sisältää alkuehtokohdan
, joka sisältää alkuehtokohdan  , niin alkuarvotehtävällä on yksikäsitteinen ratkaisu.
, niin alkuarvotehtävällä on yksikäsitteinen ratkaisu.
Normaalimuoto on tärkeä vaatimus. Esimerkiksi DY:n  ratkaisujen lukumäärä voi olla nolla tai ääretön alkuehdoista riippuen: Sijoittamalla yhtälöön
ratkaisujen lukumäärä voi olla nolla tai ääretön alkuehdoista riippuen: Sijoittamalla yhtälöön  nähdään heti, että ehto
nähdään heti, että ehto  on välttämätön ratkaisun olemassaololle. Yleisemmin korkeimman derivaatan kerroinfunktion nollakohdat hankaloittavat tilannetta, koska muuten tämä kerroin voidaan jakaa pois, ja yhtälö tulee normaalimuotoon.
on välttämätön ratkaisun olemassaololle. Yleisemmin korkeimman derivaatan kerroinfunktion nollakohdat hankaloittavat tilannetta, koska muuten tämä kerroin voidaan jakaa pois, ja yhtälö tulee normaalimuotoon.
1. kertaluvun DY:n ratkaiseminen
Lineaarinen 1. kertaluvun DY voidaan ratkaista ns. integroivan tekijän avulla. Menetelmän ideana idea on kertoa yhtälön
 molemmat puolet integroivalla tekijällä
molemmat puolet integroivalla tekijällä  , jolloin yhtälö tulee muotoon
, jolloin yhtälö tulee muotoon
Integroidaan tämän yhtälön molemmat puolet, jolloin saadaan
Tätä kaavaa ei kannata opetella ulkoa, vaan mieluummin yrittää muistaa metelmän olennaiset välivaiheet, jotta niitä pystyy soveltamaan konkreettisiin tapauksiin.
Esimerkki 1.
Ratkaistaan DY  Integroiva tehijä on
Integroiva tehijä on  , joten kerrotaan yhtälö puolittain tällä lausekkeella:
, joten kerrotaan yhtälö puolittain tällä lausekkeella:
Esimerkki 2.
Ratkaistaan alkuarvotehtävä
Kirjoitetaan yhtälö ensin normaalimuodossa:
Integroiva tekijä on nyt  Näin saadaan
Näin saadaan
Tämä on DY:n yleinen ratkaisu. Koska
 , niin alkuehto ei voi toteutua koskaan, joten alkuarvotehtävällä ei ole ratkaisua. Syy tähän on se, että alkuehto on annettu johdassa
, niin alkuehto ei voi toteutua koskaan, joten alkuarvotehtävällä ei ole ratkaisua. Syy tähän on se, että alkuehto on annettu johdassa  , jossa DY:n normaalimuotoa ei ole määritelty. Mikä tahansa muu kohta
, jossa DY:n normaalimuotoa ei ole määritelty. Mikä tahansa muu kohta  tuottaa yksikäsitteisen ratkaisun.
tuottaa yksikäsitteisen ratkaisun.
Esimerkki 3.
Muodosta  nähdään, että kyseessä on lineaarinen DY. Integroiva tekijä on
nähdään, että kyseessä on lineaarinen DY. Integroiva tekijä on

Separoituva DY
Ensimmäisen kertaluvun DY on separoituva, jos se voidaan kirjoittaa muodossa  , kun
, kun  ja
ja  ovat jatkuvia funktioita. Tulkitsemalla
ovat jatkuvia funktioita. Tulkitsemalla  epätäsmällisesti jakolaskuksi, kertomalla symbolilla
epätäsmällisesti jakolaskuksi, kertomalla symbolilla  ja jakamalla lausekkeella
ja jakamalla lausekkeella  saadaan
saadaan  .
Integroidaan vasemmalla puolella muuttujan
.
Integroidaan vasemmalla puolella muuttujan  suhteen ja oikealla muuttujan
suhteen ja oikealla muuttujan  suhteen saadaan
suhteen saadaan
Tämä on ratkaisun implisiittinen muoto, josta voidaan usein ratkaista eksplisiittisesti  . Menetelmä voidaan perustella tarkemmin käyttämällä muuttujanvaihtoa integraalissa (eli ilman
. Menetelmä voidaan perustella tarkemmin käyttämällä muuttujanvaihtoa integraalissa (eli ilman  -pyörittelyä).
-pyörittelyä).
Esimerkki 4.
Ratkaistaan DY  separointimenetelmällä. (Tämän DY:n voi poikkeuksellisesti ratkaista myös lineaarisena!)
separointimenetelmällä. (Tämän DY:n voi poikkeuksellisesti ratkaista myös lineaarisena!)
Viimeisessä vaiheessa merkittiin  yksinkertaisuuden vuoksi. Tapaus
yksinkertaisuuden vuoksi. Tapaus  on myös sallittu, sillä se johtaa triviaaliratkaisuun
on myös sallittu, sillä se johtaa triviaaliratkaisuun  , vrt. alla.
, vrt. alla.
Esimerkki 5.
Ratkaistaan alkuarvotehtävä
Koska yleistä ratkaisua ei kysytä, voidaan oikaista käyttämällä määrättyä integraalia seuraavalla tavalla:
Separoituvan DY:n eikoisratkaisut
Separointimenetelmällä saadusta yleisestä ratkaisusta puuttuu useinfunktion  nollakohtiin liittyviä erikoisratkaisuja. Syy tähän on hyvin luonnollinen, sillä jakolaskussa täytyy olettaa
nollakohtiin liittyviä erikoisratkaisuja. Syy tähän on hyvin luonnollinen, sillä jakolaskussa täytyy olettaa  . Huomataan kuitenkin, että jokaista funktion
. Huomataan kuitenkin, että jokaista funktion  nollakohtaa
nollakohtaa  vastaa DY:n
vastaa DY:n  vakioratkaisu
vakioratkaisu  , koska tällöin
, koska tällöin . Näitä ratkaisuja kutsutaan triviaaliratkaisuiksi tai erikoisratkaisuiksi (vrt. yleinen ratkaisu).
. Näitä ratkaisuja kutsutaan triviaaliratkaisuiksi tai erikoisratkaisuiksi (vrt. yleinen ratkaisu).
Jos seuraavan lauseen ehdot ovat voimassa, niin separoituvan DY:n kaikki ratkaisut saadaan yleisen ratkaisun ja erikoisratkaisujen avulla.
Lause 2.
Tarkastellaan alkuarvotehtävää  .
.
- Jos
 on jatkuva (kahden muuttujan funktio), niin on olemassa ainakin yksi ratkaisu jollakin pisteen
on jatkuva (kahden muuttujan funktio), niin on olemassa ainakin yksi ratkaisu jollakin pisteen  sisältävällä välillä.
sisältävällä välillä. - Jos lisäksi
 on jatkuvasti derivoituva muuttujan
on jatkuvasti derivoituva muuttujan  suhteen, niin alkuarvotehtävän ratkaisu on yksikäsitteinen.
suhteen, niin alkuarvotehtävän ratkaisu on yksikäsitteinen. - Yksikäsitteisyys on voimassa myö silloin, kun kohdan (i) lisäksi funktio
 on jatkuvasti derivoituva muuttujan
on jatkuvasti derivoituva muuttujan  suhteen ja
suhteen ja  .
.
Lauseen todistamisessa voidaan käyttää ns. Picardin-Lindelöfin iterointia, jonka keksi ranskalainen Emile Picard ja jota edelleen kehitti suomalainen mathemaatikko Ernst Lindelöf (1870-1946), ja muutkin.
Separoituvien DY:iden kohdalla edellinen lause saa seuraavan muodon.
Jokaisen pisteen  kautta kulkeva ratkaisukäyrä on silloin yksikäsitteinen. Erityisesti kaksi ratkaisukäyrää ei voi leikata toisiaan, eikä yksi ratkaisukäyrä voi haarautua useampaan osaan.
kautta kulkeva ratkaisukäyrä on silloin yksikäsitteinen. Erityisesti kaksi ratkaisukäyrää ei voi leikata toisiaan, eikä yksi ratkaisukäyrä voi haarautua useampaan osaan.
∴ Muut ratkaisukäyrän eivät silloin voi leikata triviaaliratkaisujen kuvaajia eli vaakasuoria  . Tällöin ehto
. Tällöin ehto  on automaattisesti voimassa muille ratkaisuille.
on automaattisesti voimassa muille ratkaisuille.
Lause 6.
Ratkaistaan lineaarinen homogeeninen DY  separointimenetelmän avulla.
separointimenetelmän avulla.
DY:llä on triviaaliratkaisu  . Muut ratkaisut eivät saa arvoa 0, joten:
. Muut ratkaisut eivät saa arvoa 0, joten:
 Separoituvaksi muuntuvat DY:t
Separoituvaksi muuntuvat DY:t
Some differential equations can made separable by using a suitable substitution.
i) ODEs of the form 
Example 7.
Let us solve the differential equation  The equation is not separable in this form, but we can make if separable by substituting
The equation is not separable in this form, but we can make if separable by substituting
 resulting to
resulting to  We get
We get
Separating the variables and integrating both sides, we get
Substituting  and simplifying yields
and simplifying yields
Here, it is not possible to derive an expression for y so we have to make do with just the implicit solution. The solutions can be visualized graphically:
As we can see, the solutions are spirals expanding in the positive direction that are suitably cut for demonstration purposes. This is clear from the solutions' polar coordinate representation which we obtain by using the substitution
Hence, the solution is
ii) ODEs of the form 
Another type of differential equation that can be made separable are equations of the form
To rewrite the equation as separable, we use the substitution 
Example 8.
Let us find the solution to the differential equation
 Eulerin menetelmä
Eulerin menetelmä
In practice, it is usually not feasible to find analytical solutions to differential equations. In these cases, the only choice for us is to resort to numerical methods. A prominent example of this kind of technique is called Euler's method. The idea behind the method is the observation made earlier with direction fields: even if we do not know the solution itself, we are still able to determine the tangents of the solution curve. In other words, we are seeking solutions for the initial value problem
In Euler's method, we begin the solving process by choosing the step length  and using the iteration formula
and using the iteration formula
The iteration starts from the index  by substituting the given initial value to the right side of the iteration formula.
Since
by substituting the given initial value to the right side of the iteration formula.
Since  is the slope of the tangent of the solution at
is the slope of the tangent of the solution at  , on each step we move the distance expressed by the step length in the direction of the
tangent. Because of this, an error occurs, which grows as the step length is increased.
, on each step we move the distance expressed by the step length in the direction of the
tangent. Because of this, an error occurs, which grows as the step length is increased.
Esimerkki 9.
Use the gadget on the right to examine the solution to the initial value problem
obtained by using Euler's method and compare the result to the precise solution.
2. ja korkeamman kertaluvun DY
Korkeamman kertaluvun differentiaaliyhtälöille on usein mahdotonta löytää jollakin yksinkertaisella lausekkeella määriteltyä ratkaisua. Tässä luvussa käsitellään tiettyjä tärkeitä erikoistapauksia, joissa ratkaisun lauseke voidaan muodostaa. Nämä ovat kaikki lineaarisia differentiaaliyhtälöitä. Keskitymme toisen kertaluvun differentiaaliyhtälöihin, koska niillä on paljon sovelluksia ja myös niiden ratkaiseminen on helpompaa, vaikkakin teoriassa hyvin samanlaista kuin korkeampien kertalukujen tapauksessa.
Homogeenisen DY:n ratkaiseminen
Toisen kertaluvun lineaariselle differentiaaliyhtälölle ei ole mitään yleistä helppoa ratkaisutapaa. Aloitamme tarkastelun homogeenisesta DY:stä
kun  ja
ja  ovat jatkuvia funktioita jollakin avoimella välillä. Tällöin pätee:
ovat jatkuvia funktioita jollakin avoimella välillä. Tällöin pätee:
1) DY:llä on lineaarisesti riippumattomat ratkaisut  ja
ja  , joita kutsutaan perusratkaisuiksi. Intuitiivinen määritelmä lineaariselle riippumattomuudelle on se, ettei suhde
, joita kutsutaan perusratkaisuiksi. Intuitiivinen määritelmä lineaariselle riippumattomuudelle on se, ettei suhde  ole vakio, ts. ratkaisut ovat tietyssä mielessä olennaisesti erilaisia.
ole vakio, ts. ratkaisut ovat tietyssä mielessä olennaisesti erilaisia.
2) DY:n yleinen ratkaisu (= kaikki ratkaisut tässä tapauksessa) voidaan esittää perusratkaisujen avulla muodossa  , kun
, kun  ja
ja  ovat vakioita.
ovat vakioita.
3) Jos kiinnitetään alkuehdot  , niin ratkaisu on yksikäsitteinen.
, niin ratkaisu on yksikäsitteinen.
Perusratkaisujen  ja
ja  löytämiseen ei ole mitään yleispätevää menetelmää, ellei sarjakehitelmiä niiksi lasketa. Tietyille yhtälötyypeille ratkaisun yleinen muoto voidaan kuitenkin arvata ja tarkistaa sijoittamalla yhtälöön.
löytämiseen ei ole mitään yleispätevää menetelmää, ellei sarjakehitelmiä niiksi lasketa. Tietyille yhtälötyypeille ratkaisun yleinen muoto voidaan kuitenkin arvata ja tarkistaa sijoittamalla yhtälöön.
Yllä esitetty menetelmä yleistyy korkeampiin kertalukuihin, mutta perusratkaisuja, yleisiä kertoimia ja alkuehtoja tarvitaan aina DY:n kertaluvun osoittama määrä.
Esimerkki 1.
Differentiaaliyhtälön  ratkaisuja ovat
ratkaisuja ovat  ja
ja  Nämä ovat lineaarisesti riippumattomia, joten DY:n yleinen ratkaisu on muotoa
Nämä ovat lineaarisesti riippumattomia, joten DY:n yleinen ratkaisu on muotoa 
Vakiokertoimiset DY:t
Yksinkertaisimpana tapauksena tarkastellaan differentiaaliyhtälöä
Yhtälön ratkaisemiseksi kokeillaan, onko sillä muotoa  olevia ratkaisuja jollakin vakion
olevia ratkaisuja jollakin vakion  arvolla. Sijoittamalla tällainen arvaus differentiaaliyhtälöön saadaan
arvolla. Sijoittamalla tällainen arvaus differentiaaliyhtälöön saadaan
Viimeinen yhtälö on nimeltään DY:n karakteristinen yhtälö. Karakteristisen yhtälön avulla saadaan alkuperäisen DY:n ratkaisuja. Karakteristisen yhtälön juurten suhteen esiintyy kolme eri tapausta:
1) Karakteristisella yhtälöllä on kaksi erisuurta reaalista juurta  . Silloin perusratkaisuiksi voidaan valita
. Silloin perusratkaisuiksi voidaan valita  ja
ja 
2) Karakteristisella yhtälöllä on (reaalinen) kaksoisjuuri  . Silloin perusratkaisuiksi voidaan valita
. Silloin perusratkaisuiksi voidaan valita  ja
ja 
3) Karakteristisen yhtälön juuret ovat kompleksilukuja ja muotoa  ,
,  . Silloin perusratkaisut ovat muotoa
. Silloin perusratkaisut ovat muotoa  ja
ja 
Toinen kohta voidaan perustella (esimerkiksi) sijoittamalla DY:ön ja kolmas kohta Eulerin kaavan  avulla. Sama idea yleistyy pienin muutoksin myös korkeampiin kertalukuihin.
avulla. Sama idea yleistyy pienin muutoksin myös korkeampiin kertalukuihin.
Koska karakterisitisen yhtälön kertoimet ovat täsmälleen samat kuin alkuperäisessä DY:ssä, niin sitä ei tarvitse joka kerta johtaa uudelleen, vaan tuloksen voi kirjoittaa suoraan DY:tä katsomalla.
Esimerkki 2.
Ratkaise reuna-arvotehtävä
Karakteristinen yhtälö on muotoa  , joten sen juuret ovat
, joten sen juuret ovat  ja
ja  Yleinen ratkaisu on siis muotoa
Yleinen ratkaisu on siis muotoa  . Vakiot kiinnittyvät reunaehtojen avulla:
. Vakiot kiinnittyvät reunaehtojen avulla:
Esimerkki 3.
Tarkastellaan korkeamman kertaluvun DY:ä
Karakteristinen yhtälö on nyt  , jonka juuret ovat
, jonka juuret ovat  ja
ja  . Perusratkaisut ovat
. Perusratkaisut ovat  ,
,  ,
,  ja
ja  . Niiden avulla saadaan yleinen ratkaisu
. Niiden avulla saadaan yleinen ratkaisu
Esimerkki 4.
Olkoon  vakio. DY:n
vakio. DY:n
 karakteristinen yhtälö on
karakteristinen yhtälö on  , jonka juuret ovat
, jonka juuret ovat  . Näin ollen
. Näin ollen  ja
ja  kolmannessa kohdassa. Koska kyseessä on ns. harmonisen oskillaattorin DY, niin käytetään muuttujana aikaa
kolmannessa kohdassa. Koska kyseessä on ns. harmonisen oskillaattorin DY, niin käytetään muuttujana aikaa  . Näin saadaan yleinen ratkaisu
. Näin saadaan yleinen ratkaisu
 , jossa
, jossa  ovat vakioita. Ne määräytyvät yksikäsitteisellä tavalla, jos tiedetään systeemin alkukohta
ovat vakioita. Ne määräytyvät yksikäsitteisellä tavalla, jos tiedetään systeemin alkukohta  ja alkunopeus
ja alkunopeus  . Kaikki ratkaisut ovat jaksollisia ja niiden jaksonaika on
. Kaikki ratkaisut ovat jaksollisia ja niiden jaksonaika on  . Oikean reunan animaatiossa
. Oikean reunan animaatiossa  ; voit itse valita kulmataajuuden
; voit itse valita kulmataajuuden  ja alkukohdan
ja alkukohdan  .
.
Eulerin lineaarinen DY
Toinen melko tavallinen 2. kertaluvun lineaarinen DY on Eulerin differentiaaliyhtälö
jossa  ja
ja  ovat vakioita. Tällainen DY voidaan ratkaista kokeilemalla muotoa
ovat vakioita. Tällainen DY voidaan ratkaista kokeilemalla muotoa  . Sijoittamalla tämä yhtälöön saadaan
. Sijoittamalla tämä yhtälöön saadaan
Tämän yhtälön juurten tyypin perusteella saadaan DY:n perusratkaisut jälleen kolmesta eri vaihtoehdosta:
1) Jos juuret ovat erisuuria reaalilukuja, niin  ja
ja  .
.
2) Jos kyseessä on reaalinen kaksoisjuuri, niin  ja
ja  .
.
3) Jos juuret ovat muotoa  , niin
, niin  ja
ja  .
.
Esimerkki 5.
Ratkaistaan DY  . Kyseessä on Eulerin differentiaaliyhtälö, joten kokeillaan yritettä
. Kyseessä on Eulerin differentiaaliyhtälö, joten kokeillaan yritettä  . Sijoittamalla saadaan
. Sijoittamalla saadaan  joten
joten  . DY:n yleinen ratkaisu on siis
. DY:n yleinen ratkaisu on siis
Epähomogeeniset DY:t
Epähomogeenisen toisen kertaluvun DY:n
yleinen ratkaisu on muotoa "vastaavan homogeenisen DY:n yleinen ratkaisu"  jokin epähomogeenisen DY:n yksittäinen ratkaisu", t.s.
jokin epähomogeenisen DY:n yksittäinen ratkaisu", t.s.
Yksittäisratkaisu  löydetään yleensä kokeilemalla (mutta systemaattisiakin menetelmiä on) muotoa "
löydetään yleensä kokeilemalla (mutta systemaattisiakin menetelmiä on) muotoa " yleisillä kertoimilla" olevia lausekkeita. Sijoittamalla tällainen yrite epähomogeeniseen DY:öön, voidaan nämä kertoimet usein ratkaista. Asia selvinnee parhaiten esimerkkien avulla.
yleisillä kertoimilla" olevia lausekkeita. Sijoittamalla tällainen yrite epähomogeeniseen DY:öön, voidaan nämä kertoimet usein ratkaista. Asia selvinnee parhaiten esimerkkien avulla.
Alla oleva taulukko antaa ohjeita yritteen valintaan silloin, kun homogeeninen osa on vakiokertoiminen ja epähomogeeninen termi on jotakin perustyyppiä. Jos  sisältää useita erilaisia taulukon funktioita, niin yritteeseen tulee mukaan kaikki vastaavat termit yleisillä kertoimilla. Taulukossa käytetään lyhennysmerkintänä karakteristista polynomia
sisältää useita erilaisia taulukon funktioita, niin yritteeseen tulee mukaan kaikki vastaavat termit yleisillä kertoimilla. Taulukossa käytetään lyhennysmerkintänä karakteristista polynomia  .
.
 sisältää sisältää |
Yritteeseen tulee mukaan |
|---|---|
 :nnen asteen polynomin :nnen asteen polynomin |
 ( (  , jos , jos  ) ) |
 |
 , jos , jos  |
 |
 , jos , jos  |
 |
 , jos , jos
 |
 |
 , jos , jos  |
 |
 , jos , jos  ja ja  |
 |
 , jos , jos  |
Huom. Muista, että toisen asteen polynomille pätee
Esimerkki 6.
Määritä DY:n  yleinen ratkaisu, kun
yleinen ratkaisu, kun
a) Sijoitettamalla yrite  saadaan
saadaan
 , josta ratkeaa
, josta ratkeaa  .
.
b) Tässä tapauksessa yrite  ei onnistu, koska se on vastaavan homogeenisen DY:n yleisen ratkaisun osa, ja tuottaa pelkän nollan, kun se sijoitetaan epähomogeenisen DY:n vasemmalle puolelle. Oikea yrite on nyt muotoa
ei onnistu, koska se on vastaavan homogeenisen DY:n yleisen ratkaisun osa, ja tuottaa pelkän nollan, kun se sijoitetaan epähomogeenisen DY:n vasemmalle puolelle. Oikea yrite on nyt muotoa  . Sijoittamalla saadaan
. Sijoittamalla saadaan

Näillä vakioiden  ja
ja  arvoilla saadaan epähomogeenisen DY:n yleinen ratkaisu, johon jää jäljelle kertoimet
arvoilla saadaan epähomogeenisen DY:n yleinen ratkaisu, johon jää jäljelle kertoimet  ja
ja  .
.
Esimerkki 7.
Edellisen esimerkin perusteella yleinen ratkaisu on  . Derivoimalla saadaan
. Derivoimalla saadaan
 . Alkuehdoista saadaan yhtälöpari
. Alkuehdoista saadaan yhtälöpari

jonka ratkaisu on  ja
ja  . Alkuarvotehtävän ratkaisu on siis
. Alkuarvotehtävän ratkaisu on siis
 .
.
Example 8.
Tyypillinen 2. kertaluvun DY:n sovellus on ns. RLC-piiri, jossa esiintyy sarjaan kytkettyinä vastus (resistanssi  ), käämi ( induktanssi
), käämi ( induktanssi  ), kondensaattori (kapasitanssi
), kondensaattori (kapasitanssi  ) ja ajasta riippuva lähdejännite
) ja ajasta riippuva lähdejännite  . Piirissä kulkeva virta
. Piirissä kulkeva virta  toteuttaa DY:n
toteuttaa DY:n  Ratkaistaan tämä DY (keinotekoisilla kertoimilla) tapauksessa
Ratkaistaan tämä DY (keinotekoisilla kertoimilla) tapauksessa 
Homogeenisen DY:n karakteristinen yhtälö on  , jonka ratkaisut ovat
, jonka ratkaisut ovat  . Näin saadaan homogeenisen DY:n perusratkaisut
. Näin saadaan homogeenisen DY:n perusratkaisut  ja
ja  . Etsitään yksittäisratkaisu yritteellä
. Etsitään yksittäisratkaisu yritteellä  . Sijoittamalla yrite epähomogeeniseen yhtälöön ja ryhmittelemällä termejä saadaan yhtälö
. Sijoittamalla yrite epähomogeeniseen yhtälöön ja ryhmittelemällä termejä saadaan yhtälö  Tämä yhtälö toteutuu kaikilla
Tämä yhtälö toteutuu kaikilla  (vain) silloin, kun
(vain) silloin, kun

josta saadaan  ja
ja  . Yleinen ratkaisu on siis muotoa
. Yleinen ratkaisu on siis muotoa
 Huom. Eksponenttitermit menevät nollaan hyvin nopeasti ("transienttivirta") ja jäljelle jää värähtely
Huom. Eksponenttitermit menevät nollaan hyvin nopeasti ("transienttivirta") ja jäljelle jää värähtely 



















































































































































































































![c\in\, ]a,b[ c\in\, ]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/6f236009a7b059c955079cfe11525d74.gif)
![S:=\{x\in [a,b]: f(x)\lt s\} S:=\{x\in [a,b]: f(x)\lt s\}](https://mycourses.aalto.fi/filter/tex/pix.php/eacb7a7945e692016628d17fe60e5153.gif)

![S\subset [a,b] S\subset [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/1c4412382a7e6967fa515506b9ec2bbc.gif)
![c:=\sup(S)\in [a,b] c:=\sup(S)\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/5dc3d86393d63fe98ba4cf254eb1874f.gif)





![c+1/k\in [a,b]\setminus S c+1/k\in [a,b]\setminus S](https://mycourses.aalto.fi/filter/tex/pix.php/c2ea33254226bed6e819ab8c9354774f.gif)












![c \in\, ]-1, 1[ c \in\, ]-1, 1[](https://mycourses.aalto.fi/filter/tex/pix.php/6a919d7f572c8fb013a2411a4499d90c.gif)







![x\in [a,b] x\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/8290bddba5acf9822dcbf61f4ac67d1b.gif)
![x_k\in [a,b] x_k\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/b4550c07770bd027aa227a5d7a44bbf8.gif)




![\lim_{j\to \infty}x_{k_{j}}= c \in [a,b] \lim_{j\to \infty}x_{k_{j}}= c \in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/0fafbfdfac0075be8df774f5e57e7659.gif)



![f\colon ]0,1]\to \mathbb{R} f\colon ]0,1]\to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/1edd3f53fa21601c9c26312f91b77db5.gif)


![c,d\in [a,b] c,d\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/768405dea1bf3697b134e29f5fb7355c.gif)



![y=\sup_{x\in [a,b]} f(x)>y-\frac{1}{k} y=\sup_{x\in [a,b]} f(x)>y-\frac{1}{k}](https://mycourses.aalto.fi/filter/tex/pix.php/b013411dfd804f02f65e8c2c55791353.gif)
![x_{k}\in [a,b] x_{k}\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2a73f7d15bff135e06fed9829c845b98.gif)



![\lim_{j\to \infty}x_{k_{j}}=d\in [a,b] \lim_{j\to \infty}x_{k_{j}}=d\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/c52627f7ca86c7368161a63752761407.gif)








![[-1, 2] [-1, 2]](https://mycourses.aalto.fi/filter/tex/pix.php/dca4fcf792a3e27e8d0e6ffd6d3dc13c.gif)







![\begin{aligned}f'(x) &=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to 0} \frac{[a(x+h)+b]-[ax+b]}{h} \\ &=\lim_{h\to 0} a \\ &=a.\end{aligned} \begin{aligned}f'(x) &=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to 0} \frac{[a(x+h)+b]-[ax+b]}{h} \\ &=\lim_{h\to 0} a \\ &=a.\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/5af936863c453fd1ea52d94c4e9b5344.gif)
















![\begin{aligned}\frac{(f+g)(x+h)-(f+g)(x)}{h} \ & \ = \ \frac{[f(x+h)+g(x+h)]-[f(x)+g(x)]}{h} \\ & \ = \ \frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\end{aligned} \begin{aligned}\frac{(f+g)(x+h)-(f+g)(x)}{h} \ & \ = \ \frac{[f(x+h)+g(x+h)]-[f(x)+g(x)]}{h} \\ & \ = \ \frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/ef8575955c1913eb61f3bda0de6c3ee8.gif)













![\begin{aligned}\frac{d}{dx} [(x^4-2)(2x+1)] &= \frac{d}{dx}(x^4-2) \cdot (2x+1) + (x^4-2) \cdot \frac{d}{dx}(2x + 1) \\ &= 4x^3(2x+1) + 2(x^4-2) \\ &= 8x^4+4x^3+2x^4-4 \\ &= 10x^4+4x^3-4.\end{aligned} \begin{aligned}\frac{d}{dx} [(x^4-2)(2x+1)] &= \frac{d}{dx}(x^4-2) \cdot (2x+1) + (x^4-2) \cdot \frac{d}{dx}(2x + 1) \\ &= 4x^3(2x+1) + 2(x^4-2) \\ &= 8x^4+4x^3+2x^4-4 \\ &= 10x^4+4x^3-4.\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/8c708f0f3c9ec809601fbd059363c2b4.gif)
![\frac{d}{dx} [(x^4-2)(2x+1)] = \frac{d}{dx} (2x^5 +x^4 -4x -2) = 10x^4 +4x^3 -4. \frac{d}{dx} [(x^4-2)(2x+1)] = \frac{d}{dx} (2x^5 +x^4 -4x -2) = 10x^4 +4x^3 -4.](https://mycourses.aalto.fi/filter/tex/pix.php/d030d685c2973158b90ad35a97a50d5b.gif)







![x_0\in \, ]a,b[ x_0\in \, ]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/b4b89672d69ecf8369f43f7dd31f0d2c.gif)

![]x_0-\delta,x_0+\delta[ ]x_0-\delta,x_0+\delta[](https://mycourses.aalto.fi/filter/tex/pix.php/c9bd44b465175498c9476b6701b55fca.gif)





![c\in \, ]x_0,x[ c\in \, ]x_0,x[](https://mycourses.aalto.fi/filter/tex/pix.php/5c97c28ce97d3f291e533efe3f450068.gif)


![\begin{aligned}\sin'(t) & = \lim_{h\to 0} \frac{\sin(t+h)-\sin(t)}{h} \\
& = \lim_{h\to 0} \frac{[\sin(t)\cos(h)+\cos(t)\sin(h)]-\sin(t)}{h} \\
& = \lim_{h\to 0}\sin(t)\frac{\cos(h)-1}{h}+\lim_{h\to 0}\cos(t)\frac{\sin(h)}{h}.
\end{aligned} \begin{aligned}\sin'(t) & = \lim_{h\to 0} \frac{\sin(t+h)-\sin(t)}{h} \\
& = \lim_{h\to 0} \frac{[\sin(t)\cos(h)+\cos(t)\sin(h)]-\sin(t)}{h} \\
& = \lim_{h\to 0}\sin(t)\frac{\cos(h)-1}{h}+\lim_{h\to 0}\cos(t)\frac{\sin(h)}{h}.
\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/43dab0c7e1606d265f8428433a47b025.gif)
























![\frac{f(g(x+h))-f(g(x))}{h}=[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}. \frac{f(g(x+h))-f(g(x))}{h}=[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}.](https://mycourses.aalto.fi/filter/tex/pix.php/4772424382ad3806e0cca96db8c05fd1.gif)

![[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}\to f'(g(x))g'(x). [E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}\to f'(g(x))g'(x).](https://mycourses.aalto.fi/filter/tex/pix.php/57e9195f36e9ff554cd408a7b174bd50.gif)

















![x_0\in [a,b] x_0\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/f1f8b7afdbcc5f31096799e43c43711e.gif)

























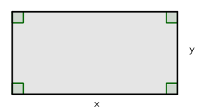

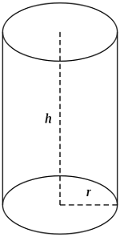













![f[A]=B f[A]=B](https://mycourses.aalto.fi/filter/tex/pix.php/c0dfc65c448fbf8cef4d8969eab57661.gif)




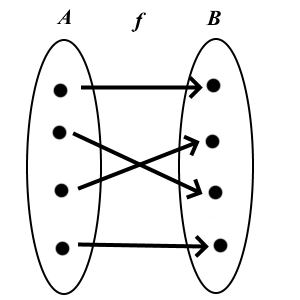
















![\sin \colon [-\pi/2,\pi/2]\to [-1,1]
\sin \colon [-\pi/2,\pi/2]\to [-1,1]](https://mycourses.aalto.fi/filter/tex/pix.php/8516ac159a27828b8807ae8346208684.gif)
![\cos \colon [0,\pi] \to [-1,1]
\cos \colon [0,\pi] \to [-1,1]](https://mycourses.aalto.fi/filter/tex/pix.php/7b6724fb6d58f64ba500defadc44773d.gif)
![\tan \colon ]-\pi/2,\pi/2[\, \to \mathbb{R}
\tan \colon ]-\pi/2,\pi/2[\, \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/04f0656b3b1805879518b5a4d600ae97.gif)
![\arctan \colon \mathbb{R}\to \ ]-\pi/2,\pi/2[, \arctan \colon \mathbb{R}\to \ ]-\pi/2,\pi/2[,](https://mycourses.aalto.fi/filter/tex/pix.php/5a0cfc94ec76b4bb98759ea997a6814e.gif)
![\arcsin \colon [-1,1]\to [-\pi/2,\pi/2], \arcsin \colon [-1,1]\to [-\pi/2,\pi/2],](https://mycourses.aalto.fi/filter/tex/pix.php/c4d09554c2fd5fc1cbf2d81a599c1b95.gif)
![\arccos \colon [-1,1]\to [0,\pi] \arccos \colon [-1,1]\to [0,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/ae1f9e9c619a7daceef40e2227521839.gif)
![x = \tan \alpha \Leftrightarrow \alpha = \arctan x \ \ \text{for } \alpha \in \ ]-\pi/2,\pi/2[ x = \tan \alpha \Leftrightarrow \alpha = \arctan x \ \ \text{for } \alpha \in \ ]-\pi/2,\pi/2[](https://mycourses.aalto.fi/filter/tex/pix.php/1e8adfc9de7373123d3e37d24295583b.gif)
![x = \sin \alpha \Leftrightarrow \alpha = \arcsin x \ \ \text{for } \alpha \in \, [-\pi/2,\pi/2] x = \sin \alpha \Leftrightarrow \alpha = \arcsin x \ \ \text{for } \alpha \in \, [-\pi/2,\pi/2]](https://mycourses.aalto.fi/filter/tex/pix.php/e0f134a17e198c541c553b3c2e9305f0.gif)
![x = \cos \alpha \Leftrightarrow \alpha = \arccos x \ \ \text{for } \alpha \in \, [0,\pi] x = \cos \alpha \Leftrightarrow \alpha = \arccos x \ \ \text{for } \alpha \in \, [0,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/eab3cb1a5193c48cde03e2046ec37027.gif)
















![\exp\colon\mathbb{R}\to\, ]0,\infty[ \exp\colon\mathbb{R}\to\, ]0,\infty[](https://mycourses.aalto.fi/filter/tex/pix.php/463736f26c065deb116e8539cc1e1c90.gif)
















![\ln\colon \ ]0,\infty[ \ \to \mathbb{R}
\ln\colon \ ]0,\infty[ \ \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/a57877163d9051a40ddff6a55fb8ea50.gif)










































![f\colon\left[-1,1\right] f\colon\left[-1,1\right]](https://mycourses.aalto.fi/filter/tex/pix.php/8fa1143ca458419d8b2c9fe6b3bc7b98.gif)













![p=\inf_{x\in\left[a,b\right]}f(x) p=\inf_{x\in\left[a,b\right]}f(x)](https://mycourses.aalto.fi/filter/tex/pix.php/df0ba13db5d97e1ab617c25bf3f053f3.gif)
![s=\sup_{x\in\left[a,b\right]}f(x) s=\sup_{x\in\left[a,b\right]}f(x)](https://mycourses.aalto.fi/filter/tex/pix.php/74dbac954365a4026b75091df793c18d.gif)





![c\in\,]a,b[ c\in\,]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/0645c1a33227f3466be2997827a643b5.gif)

![x\in\,]a,b[ x\in\,]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/72fa533e00aaedd77d6d52d82313b48e.gif)

![c\in\,[x,x+h] c\in\,[x,x+h]](https://mycourses.aalto.fi/filter/tex/pix.php/318888fc5bb357cd31a47f39bdaf0103.gif)
































![\left[x,x+\Delta x\right] \left[x,x+\Delta x\right]](https://mycourses.aalto.fi/filter/tex/pix.php/4d8fd407309f8f47e5b678de4fddac7f.gif)



![\left[a,\infty\right[,\left]-\infty,b\right] \left[a,\infty\right[,\left]-\infty,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/6d8fe0a29c1bae92fcd9c6684a5d437c.gif)





























































































































