Differentiaali- ja integraalilaskenta 2
| Site: | MyCourses |
| Course: | MS-A0201 - Differentiaali- ja integraalilaskenta 2 (TFM), Luento-opetus, 9.1.2024-19.2.2024 |
| Book: | Differentiaali- ja integraalilaskenta 2 |
| Printed by: | Guest user |
| Date: | Wednesday, 11 December 2024, 10:29 AM |
1. Taso- ja avaruuskäyrät
1.1. Parametrisointi
Parametrisointi
Muodollisesti käyrällä tarkoitetaan parametrisoitua joukkoa  , joka voidaan esittää muodossa
, joka voidaan esittää muodossa
 missä
missä  on väli ja funktio
on väli ja funktio  on jatkuva.
Vektoriarvoisen funktion
on jatkuva.
Vektoriarvoisen funktion  jatkuvuus tarkoittaa, että sen kaikki koordinaattifunktiot ovat jatkuvia missä tahansa kantaesityksessä.
jatkuvuus tarkoittaa, että sen kaikki koordinaattifunktiot ovat jatkuvia missä tahansa kantaesityksessä.
Funktio  on eräs käyrän
on eräs käyrän  parametrisointi ja
parametrisointi ja  on tätä parametrisointia vastaava parametriväli.
Väli
on tätä parametrisointia vastaava parametriväli.
Väli  voi olla avoin
voi olla avoin  , suljettu
, suljettu ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) tai puoliavoin
tai puoliavoin ![(a,b],\,[a,b) (a,b],\,[a,b)](https://mycourses.aalto.fi/filter/tex/pix.php/bf492f2250f45ec12514122fc88339c6.gif) ja myös rajoittamaton.
ja myös rajoittamaton.
Avaruuskäyrän ( ) parametrisointi voidaan antaa muodossa
) parametrisointi voidaan antaa muodossa
 Vaihtoehtoisesti voidaan myös käyttää koordinaattimuotoa
Vaihtoehtoisesti voidaan myös käyttää koordinaattimuotoa
 tai vektorimuotoa
tai vektorimuotoa
 jossa
jossa  ja
ja  ovat
ovat  :n luonnolliset kantavektorit. Myös pystyvektoriesitys
:n luonnolliset kantavektorit. Myös pystyvektoriesitys ![[x(t),y(t),z(t)]^T [x(t),y(t),z(t)]^T](https://mycourses.aalto.fi/filter/tex/pix.php/ac191007218c1cf472a6ef725b1f7043.gif) voi olla hyödyllinen, jos parametrisointiin halutaan soveltaa matriisioperaatioita kuten kiertoja tai peilauksia.
voi olla hyödyllinen, jos parametrisointiin halutaan soveltaa matriisioperaatioita kuten kiertoja tai peilauksia.
Edellä funktion  jatkuvuus tarkoittaa siis koordinaattifunktioiden
jatkuvuus tarkoittaa siis koordinaattifunktioiden  jatkuvuutta parametrivälillä
jatkuvuutta parametrivälillä  .
.
Huomautus. Samalla käyrällä on useita eri parametrisointeja. Miksi? Kuinka pääset yhdestä parametrisoinnista toiseen?
Esimerkki, suora tasossa
Kahden  -tason pisteen
-tason pisteen  ja
ja  kautta kulkeva suora voidaan parametrsioida
kautta kulkeva suora voidaan parametrsioida
 Havaitaan, että
Havaitaan, että  joten valitsemalla
parametriväliksi
joten valitsemalla
parametriväliksi ![I=[0,1] I=[0,1]](https://mycourses.aalto.fi/filter/tex/pix.php/e56ebb3d9782176e00be7a6f25e2f8df.gif) saadaan pisteitä
saadaan pisteitä  ja
ja  yhdistävä jana.
yhdistävä jana.
Esimerkki, reaalifunktion kuvaaja
Jatkuvan funktion ![f\colon[a,b]\rightarrow\mathbb{R} f\colon[a,b]\rightarrow\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/f512365dad0a1a2382aa289ee8bfceea.gif) kuvaaja
kuvaaja  voidaan ajatella
voidaan ajatella  -tason käyränä. Tämä käyrä voidaan parametrisoida
-tason käyränä. Tämä käyrä voidaan parametrisoida
 missä
missä ![t\in[a,b] t\in[a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/37b02e50d3262a530368502875a76e1c.gif) . Tai vastaavasti vektorimuodossa
. Tai vastaavasti vektorimuodossa

Esimerkki, Helix-käyrä eli kierrejousi
Helix-käyrä eli kierrejousi voidaan parametrisoida
 missä
missä  ovat parametreja. Parametri
ovat parametreja. Parametri  on jousen säde ja parametria
on jousen säde ja parametria  voidaan ajatella jousen venymänä.
voidaan ajatella jousen venymänä.
Vaihtoehtoisesti voidaan tietysti tässäkin käyttää myös vektorimuotoa

Suunta
Usein parametriväli on suljettu väli ![I=[a,b] I=[a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/aa922a30ce1173792a5bbaaeec5dd22c.gif) . On lisäksi mahdollista, että
. On lisäksi mahdollista, että  tai
tai  .
.
Parametrisointi määrää käyrälle positiivisen suunnan, jolloin  on käyrän alkupiste ja
on käyrän alkupiste ja  sen päätepiste.
Käyrää, jonka alku- ja päätepiste ovat samoja kutsutaan umpinaiseksi (engl. 'closed').
sen päätepiste.
Käyrää, jonka alku- ja päätepiste ovat samoja kutsutaan umpinaiseksi (engl. 'closed').
Voidaan muodostaa myös vastakkainen parametrisointi, jossa käyrä pysyy samana, mutta sen kulkusuunta vaihtuu. Tällöin myös parametrisointiin liittyvät alku- ja päätepiste vaihtuvat toisikseen.
Esimerkiksi tapauksessa ![\mathbf{r}\colon[0,1]\rightarrow C \mathbf{r}\colon[0,1]\rightarrow C](https://mycourses.aalto.fi/filter/tex/pix.php/3134a15d54433f472a41b7dfaaa47509.gif) vastakkainen parametrisointi
vastakkainen parametrisointi  saadaan helposti kaavalla
saadaan helposti kaavalla
![\mathbf{r}_{-}(t)=\mathbf{r}(1-t), \quad t\in [0,1]. \mathbf{r}_{-}(t)=\mathbf{r}(1-t), \quad t\in [0,1].](https://mycourses.aalto.fi/filter/tex/pix.php/1c2a838f4035abc9bda4820175b2d786.gif)
Esimerkki, ympyrän kehä tasossa
Olkoon  ja
ja  .
.  -keskisen ja
-keskisen ja  -säteisen ympyrän kehän parametrisoinniksi saadaan
-säteisen ympyrän kehän parametrisoinniksi saadaan
 Jos halutaan parametrisoida koko kehä, voidaan parametriväliksi valita esimerkiksi
Jos halutaan parametrisoida koko kehä, voidaan parametriväliksi valita esimerkiksi ![[0,2\pi] [0,2\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/1cc5fb6d3b10cf0b4029e23d46fa7fc0.gif) tai
tai ![[-\pi,\pi] [-\pi,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/a5d4b5c6dcadd17bce3289ba1891d927.gif) .
Lisäksi havaitaan, että
.
Lisäksi havaitaan, että  ja
ja  joten käyrä on umpinainen.
joten käyrä on umpinainen.
Suunnistus voidaan vaihtaa päinvastaiseksi korvaamalla  parametrisoinnissa. Tällöin
parametrisoinnissa. Tällöin  ,
,  ja
ja

Implisiittinen muoto
Tasokäyrän yhtälö voidaan usein ilmaista myös implisiittisessä muodossa  , missä
, missä  on jokin kahden muuttujan lauseke.
Konkreettisia esimerkkejä ovat funktion kuvaaja
on jokin kahden muuttujan lauseke.
Konkreettisia esimerkkejä ovat funktion kuvaaja  , joka voidaan määritellä muodossa
, joka voidaan määritellä muodossa  , ja
, ja  -säteinen ympyrä
-säteinen ympyrä  .
.
Huomautus. Yleisessä tapauksessa yhtälön  määräämä tasojoukko voi olla hyvin yllättävän näköinen.
Jos esimerkiksi
määräämä tasojoukko voi olla hyvin yllättävän näköinen.
Jos esimerkiksi  on mikä tahansa suljettu tasojoukko (reunapisteet kuuluvat joukkoon), niin funktio
on mikä tahansa suljettu tasojoukko (reunapisteet kuuluvat joukkoon), niin funktio

 on jatkuva, mutta yhtälö
on jatkuva, mutta yhtälö  esittää koko alkuperäistä joukkoa
esittää koko alkuperäistä joukkoa  .
.
1.2. Tangenttivektori
Käyrän tangentti
Tarkastellaan 3-ulotteista parametrisointia  , joka on derivoituva.
Tämä tarkoittaa, että vektorin
, joka on derivoituva.
Tämä tarkoittaa, että vektorin  jokaisen koordinaattifunktion täytyy olla derivoituva.
jokaisen koordinaattifunktion täytyy olla derivoituva.
Parametriväliä ![[t,t+\Delta t] [t,t+\Delta t]](https://mycourses.aalto.fi/filter/tex/pix.php/e9ceeb8058726ba0a6fb37e1363a2cb3.gif) vastaava käyrän sekantti on vektori
vastaava käyrän sekantti on vektori
 Kun
Kun  , niin
, niin  kääntyy yhä enemmän käyrän tangentin suuntaiseksi, mutta samalla sen pituus kutistuu kohti nollaa.
Skaalamalla kertoimella
kääntyy yhä enemmän käyrän tangentin suuntaiseksi, mutta samalla sen pituus kutistuu kohti nollaa.
Skaalamalla kertoimella  saadaan kuitenkin erotusosamäärää vastaava lauseke, josta nähdään, että raja-arvo
saadaan kuitenkin erotusosamäärää vastaava lauseke, josta nähdään, että raja-arvo
 on olemassa ja se voidaan käytännössä laskea kaavalla
on olemassa ja se voidaan käytännössä laskea kaavalla
 Vektorin
Vektorin  ensimmäinen koordinaatti on nimittäin
ensimmäinen koordinaatti on nimittäin
 ja samoin käy myös muissa koordinaateissa. Tämän vuoksi määritelmä näyttää järkevältä.
ja samoin käy myös muissa koordinaateissa. Tämän vuoksi määritelmä näyttää järkevältä.
Määritelmä. Jos käyrällä  on derivoituva parametrisointi
on derivoituva parametrisointi  , niin pisteessä
, niin pisteessä  vektori
vektori
 on käyrän tangenttivektori. Tason tapauksessa
on käyrän tangenttivektori. Tason tapauksessa  -koordinaatti jää tietysti pois.
-koordinaatti jää tietysti pois.
Fysikaalisessa tulkinnassa  on käyrää
on käyrää  pitkin liikkuvan kappaleen hetkellinen nopeus ja
pitkin liikkuvan kappaleen hetkellinen nopeus ja  kappaleen vauhti hetkellä
kappaleen vauhti hetkellä  . Lisäksi
. Lisäksi
 on kappaleen hetkellinen kiihtyvyys.
on kappaleen hetkellinen kiihtyvyys.
Huomautus. Tangenttivektorin määritelmästä saadaan lisäksi hyödyllinen approksimaatio:
 Muistisääntö: Siirtymä on suunnilleen sama kuin alkunopeus kertaa aikavälin pituus.
Muistisääntö: Siirtymä on suunnilleen sama kuin alkunopeus kertaa aikavälin pituus.
Esimerkki
Sykloidi kuvaa vierivään renkaaseen tarttuneen hiukkasen ratakäyrää. Se voidaan parametrisoida kulman  avulla muodossa
avulla muodossa
 Tangenttivektoriksi saadaan tällöin
Tangenttivektoriksi saadaan tällöin
 ja edelleen voidaan ratkaista kiihtyvyys
ja edelleen voidaan ratkaista kiihtyvyys
 Tästä seuraa
Tästä seuraa  tasaisen pyörimisliikkeen kiihtyvyys.
tasaisen pyörimisliikkeen kiihtyvyys.
Huomautus. Sykloidin parametrisoinnissa  , eli hetkellinen nopeus on nolla (niissä kohdissa, joissa hiukkanen koskettaa vierimisalustaa, vrt. yllä.).
Tällöin käyrän suunta voi muuttua jyrkästi, vaikka sen parametrisointi onkin jatkuvasti derivoituva.
, eli hetkellinen nopeus on nolla (niissä kohdissa, joissa hiukkanen koskettaa vierimisalustaa, vrt. yllä.).
Tällöin käyrän suunta voi muuttua jyrkästi, vaikka sen parametrisointi onkin jatkuvasti derivoituva.
1.3. Kaarenpituus
Kaarenpituus
Olkoon ![\mathbf{r}\colon[a,b]\rightarrow\mathbb{R}^n \mathbf{r}\colon[a,b]\rightarrow\mathbb{R}^n](https://mycourses.aalto.fi/filter/tex/pix.php/ae71efff2bf5119390c4e5f06578200d.gif) käyrän
käyrän  jatkuvasti derivoituva parametrisointi.
Jos käyrää approksimoidaan sekanteista muodostetulla murtoviivalla ja annetaan approksimaation tihentyä, voidaan havaita murtoviivan pituuden suppenevan kohti kaaren pituutta
jatkuvasti derivoituva parametrisointi.
Jos käyrää approksimoidaan sekanteista muodostetulla murtoviivalla ja annetaan approksimaation tihentyä, voidaan havaita murtoviivan pituuden suppenevan kohti kaaren pituutta  .
.
Kaarenpituus (tai käyränpituus) voidaankin määrittää integraalina
 missä merkintä
missä merkintä  tarkoittaa vektorin (euklidista) normia eli pituutta avaruudessa
tarkoittaa vektorin (euklidista) normia eli pituutta avaruudessa  . Tapauksessa
. Tapauksessa  on siis
on siis  .
.
Perustelu. Olkoot  välin
välin ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) ositus. Tällöin vektorien
ositus. Tällöin vektorien  ja
ja  välisen sekanttivektorin lauseke on
välisen sekanttivektorin lauseke on
 (vrt. aiempaan määritelmään, kun
(vrt. aiempaan määritelmään, kun  ).
).
Toisaalta sekanttivektorien pituudelle pätee approksimaatio
 joten kaarenpituuden approksimaatioksi
joten kaarenpituuden approksimaatioksi  kappaleella sekanttivektoreita saadaan
kappaleella sekanttivektoreita saadaan
 Vaaditaan lisäksi, että jokaisen jakovälin pituus
Vaaditaan lisäksi, että jokaisen jakovälin pituus  suppenee kohti nollaa, kun
suppenee kohti nollaa, kun  , jolloin edellinen lauseke on funktion
, jolloin edellinen lauseke on funktion
 Riemannin summa. Toisaalta, kun jakovälejä tihennetään, lähestyy approksimaatio kaaren todellista pituutta.
Näin ollen integraalin määritelmästä seuraa
Riemannin summa. Toisaalta, kun jakovälejä tihennetään, lähestyy approksimaatio kaaren todellista pituutta.
Näin ollen integraalin määritelmästä seuraa

Jos käyrän parametrisointi on ainoastaan paloittain jatkuvasti derivoituva, saadaan koko käyrän kaarenpituus laskemalla osien kaarenpituudet yhteen.
Vaikka käyrällä onkin aina äärettömän monta eri parametrisointia, voidaan osoittaa, ettei kaarenpituus riipu (injektiivisen) parametrisoinnin valinnasta eikä suunnasta.
Esimerkki
Määritetään Helix-käyrän  kaarenpituus parametrivälillä
kaarenpituus parametrivälillä ![t\in[0,2\pi] t\in[0,2\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/fe633d652f3e72a8166a95d781b83845.gif) . Tangenttivektoriksi saadaan
. Tangenttivektoriksi saadaan
 joten
joten
 Kaarenpituudeksi saadaan
Kaarenpituudeksi saadaan

Esimerkki
Johdetaan kaava funktion kuvaajan  kaarenpituudelle välillä
kaarenpituudelle välillä ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) . Asetetaan
. Asetetaan  , kun
, kun ![t\in[a,b] t\in[a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/37b02e50d3262a530368502875a76e1c.gif) . Tällöin
. Tällöin
 joten kaarenpituudeksi saadaan
joten kaarenpituudeksi saadaan

Huomautus. Kaarenpituutta voidaan tutkia myös sellaisille käyrille, joiden parametrisointi on muodostettu rajoittamattomalla välillä tai käyrä on "rajoittamaton" tai "itsensä päälle laskostuva" avoimen parametrivälinsä päätepisteen läheisyydessä. Kaarenpituusintegraalista tulee tällöin epäoleellinen. Jos tämä integraali on suppeneva, niin käyrää kutsutaan suoristuvaksi.
Esimerkki
Olkoot käyrällä parametrisointi  , kun
, kun  . Lasketaan tälle kaarenpituus.
. Lasketaan tälle kaarenpituus.
Tangenttivektorin  pituus on
pituus on  , joten kaarenpituudeksi saadaan nyt
, joten kaarenpituudeksi saadaan nyt
2. Usean muuttujan funktiot
Usean muuttujan funktiot
Usean muuttujan reaaliarvoisella funktiolla tarkoitetaan funktiota  , missä
, missä  ,
,  on funktion
määrittelyjoukko. Tällainen funktio siis liittää reaalisiin parametreihin
on funktion
määrittelyjoukko. Tällainen funktio siis liittää reaalisiin parametreihin  reaaliluvun
reaaliluvun  .
Joskus (erityisesti fysiikassa) tällaista funktiota sanotaan skalaarikentäksi.
.
Joskus (erityisesti fysiikassa) tällaista funktiota sanotaan skalaarikentäksi.
Esimerkiksi kaava  määrittelee kahden muuttujan
määrittelee kahden muuttujan  funktion. Tämän funktion arvo on sylinterin tilavuus, kun
funktion. Tämän funktion arvo on sylinterin tilavuus, kun  on sen säde ja
on sen säde ja  korkeus. Tähän sovellukseen liittyvä funktion määrittelyjoukko on tason ensimmäinen neljännes,
korkeus. Tähän sovellukseen liittyvä funktion määrittelyjoukko on tason ensimmäinen neljännes,
 mutta funktion määräävä matemaattinen kaava on kuitenkin määritelty ja mielekäs kaikilla
mutta funktion määräävä matemaattinen kaava on kuitenkin määritelty ja mielekäs kaikilla  , siis myös negatiivisilla luvuilla.
, siis myös negatiivisilla luvuilla.
2.1. Osittaisderivaatta
Avoin joukko
Avoimessa joukossa voidaan jokaisesta pisteestä siirtyä ainakin lyhyt etäisyys kaikkiin mahdollisiin suuntiin. Tällaisessa joukossa määritellyn funktion arvojen muutosta voidaan siis tutkia kaikissa eri suunnissa, mikä on tärkeää funktion osittaisderivaattojen tapauksessa. Tarkemmin:Määritelmä
Joukko on avoin, jos sen jokaille pisteelle
on avoin, jos sen jokaille pisteelle  löytyy sellainen
löytyy sellainen  , että
, että
 Joukko
Joukko  on pallo(n sisäpuoli), jonka keskipiste on
on pallo(n sisäpuoli), jonka keskipiste on  ja säde
ja säde  .
Tasossa käytetään myös nimitystä kiekko, mutta merkintä
.
Tasossa käytetään myös nimitystä kiekko, mutta merkintä  = 'ball' sopii kaikkiin ulottuvuuksiin. Englannin kielen sana 'sphere' käännetään myös palloksi, mutta sekaannusten välttämiseksi siitä on matematiikassa toisinaan hyvä käyttää nimitystä "pallopinta".
= 'ball' sopii kaikkiin ulottuvuuksiin. Englannin kielen sana 'sphere' käännetään myös palloksi, mutta sekaannusten välttämiseksi siitä on matematiikassa toisinaan hyvä käyttää nimitystä "pallopinta".
Osittaisderivaatta
Olkoon ,
,  avoin ja
avoin ja  funktio. Tällöin kaikille
funktio. Tällöin kaikille  funktion
funktion  osittaisderivaatta muuttujan
osittaisderivaatta muuttujan  suhteen on
suhteen on
 jos kyseinen raja-arvo on olemassa. Tässä
jos kyseinen raja-arvo on olemassa. Tässä  on
on  :s yksikkökantavektori.
:s yksikkökantavektori.
Huom. Erityisesti tapauksissa  ja
ja  tai
tai  käytetään osittaisderivaatoille yleensä merkintöjä
käytetään osittaisderivaatoille yleensä merkintöjä

 on
on
 ja
ja

Käytännössä osittaisderivointi jonkin muuttujan suhteen tapahtuu samaan tapaan kuin yhden muuttujan tapauksessa, muistetaan vain tulkita kaikki muut muuttujat ikään kuin vakioiksi.
Syy: Esimerkiksi kahden muuttujan funktiosta  voidaan muodostaa yhden muuttujan
funktio
voidaan muodostaa yhden muuttujan
funktio  kiinnittämällä muuttuja
kiinnittämällä muuttuja  . Tällöin funktion
. Tällöin funktion  tavallinen yhden muuttujan erotusosamäärä on sama lauseke kuin funktion
tavallinen yhden muuttujan erotusosamäärä on sama lauseke kuin funktion  erotusosamäärässä ensimmäisen muuttujan suhteen:
erotusosamäärässä ensimmäisen muuttujan suhteen:

Esimerkki
Esimerkki
Olkoon funktio  ,
,  Sen osittaisderivaatat ovat
Sen osittaisderivaatat ovat

Merkintätavat osittaisderivaatoille
Funktion  osittaisderivaattaa muuttujan
osittaisderivaattaa muuttujan  suhteen merkitään mm. seuraavilla tavoilla
suhteen merkitään mm. seuraavilla tavoilla

Tapauksessa  usein kirjoitetaan
usein kirjoitetaan  , jolloin voidaan myös käyttää merkintöjä
, jolloin voidaan myös käyttää merkintöjä

Osittaisderivaatalle käytetään erillistä symbolia  ("doo"), jotta se ei sekoittuisi tavalliseen derivaattaan.
Tähän palataan vähän myöhemmin ketjusäännön yhteydessä.
("doo"), jotta se ei sekoittuisi tavalliseen derivaattaan.
Tähän palataan vähän myöhemmin ketjusäännön yhteydessä.
Osittaisderivaatan arvo
Funktion  osittaisderivaatan
osittaisderivaatan  arvoa pisteessä
arvoa pisteessä  merkitään
merkitään
 jossa muuttuja
jossa muuttuja  määritellään
määritellään  .
.
Esimerkiksi, jos  ja
ja  , niin
\begin{align}
f_{u}(\mathbf{w})&=f_{u}(x^2,xy) =\left.\bigg(\frac{\partial}{\partial u}f(u,v)\bigg)\right|_{(x^2,xy)} \\
&=2uv\Big|_{u=x^2,\,v=xy}= 2(x^2)(xy)=2x^3y.
\end{align}
, niin
\begin{align}
f_{u}(\mathbf{w})&=f_{u}(x^2,xy) =\left.\bigg(\frac{\partial}{\partial u}f(u,v)\bigg)\right|_{(x^2,xy)} \\
&=2uv\Big|_{u=x^2,\,v=xy}= 2(x^2)(xy)=2x^3y.
\end{align}
Esimerkki
Lasketaan
 kun
kun  . Tällöin saadaan
. Tällöin saadaan

Esimerkki
Etsitään  , kun
, kun  . Tästä saadaan
. Tästä saadaan
 Siten
Siten

Ketjusäännön soveltaminen
Tavallisiin derivaattoihin liittyvä ketjusääntö
 on voimassa myös osittaisderivaattojen tapauksessa.
Jos esimerkiksi
on voimassa myös osittaisderivaattojen tapauksessa.
Jos esimerkiksi  ja
ja  niin
niin
 ja
ja
 Myöhemmin esitetään myös ketjusääntö monen muuttujan funktioille.
Myöhemmin esitetään myös ketjusääntö monen muuttujan funktioille.
Esimerkki
Osoitetaan, että derivoituva funktio  toteuttaa seuraavan osittaisdifferentiaaliyhtälön, kun
toteuttaa seuraavan osittaisdifferentiaaliyhtälön, kun  :
:
 Ketjusäännön perusteella
Ketjusäännön perusteella
 Siten
Siten

Korkeammat osittaisderivaatat
Funktiolle  voidaan määritellä myös korkeampia osittaisderivaattoja.
Jos
voidaan määritellä myös korkeampia osittaisderivaattoja.
Jos  , niin saadaan esimerkiksi
, niin saadaan esimerkiksi
 ja
ja
 Vastaavasti, jos
Vastaavasti, jos  , saadaan vaikkapa
, saadaan vaikkapa

Esimerkki
Etsitään funktion  toiset osittaisderivaatat. Saadaan aluksi
toiset osittaisderivaatat. Saadaan aluksi
 Siten
\begin{align*}
f_{xx}(x,y)&=\frac{\partial }{\partial x}3x^2y^4=6xy^4, \\
f_{yx}(x,y)&=\frac{\partial}{\partial x}4x^3y^3=12x^2y^3, \\
f_{xy}(x,y)&=\frac{\partial}{\partial y}3x^2y^4=12x^2y^3, \\
f_{yy}(x,y)&=\frac{\partial }{\partial y}4x^3y^3=12x^3y^2.
\end{align*}
Siten
\begin{align*}
f_{xx}(x,y)&=\frac{\partial }{\partial x}3x^2y^4=6xy^4, \\
f_{yx}(x,y)&=\frac{\partial}{\partial x}4x^3y^3=12x^2y^3, \\
f_{xy}(x,y)&=\frac{\partial}{\partial y}3x^2y^4=12x^2y^3, \\
f_{yy}(x,y)&=\frac{\partial }{\partial y}4x^3y^3=12x^3y^2.
\end{align*}
Huom. Edellisestä voidaan havaita, että  . Tämä ei ole sattumaa!
. Tämä ei ole sattumaa!
Jos funktio  sekä sen osittaisderivaatat
sekä sen osittaisderivaatat  ja
ja  ovat kaikki jatkuvia, niin
ovat kaikki jatkuvia, niin
 Toisin sanoen derivoimisjärjestyksellä ei ole tällöin väliä. Vastaava tulos pätee myös yleisesti kaikilla
Toisin sanoen derivoimisjärjestyksellä ei ole tällöin väliä. Vastaava tulos pätee myös yleisesti kaikilla  .
.
2.2. Tangenttitaso ja normaalisuora
Pinnan tangentti ja normaali
Yhden muuttujan tapauksessa derivaatan avulla voidaan löytää lauseke derivoituvan funktion tangentille annetussa pisteessä.
Normaali on kohtisuorassa tangenttia vastaan.
Pinnalle  saadaan puolestaan kaksi tangenttivektoria pisteessä
saadaan puolestaan kaksi tangenttivektoria pisteessä  käyrien
käyrien  ja
ja  tangentteina:
tangentteina:

Pinnan (ylä)normaalivektori  on kohtisuorassa
näitä molempia tangenttivektoreita vastaan. Siksi se saadaan ristitulona
\begin{align*}
\mathbf{N} &= \mathbf{T}_1\times \mathbf{T}_2 =
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
1 & 0 & f_{x}(a,b) \\
0 & 1 & f_{y}(a,b)
\end{vmatrix}
=-f_{x}(a,b)\mathbf{i} - f_{y}(a,b)\mathbf{j} + \mathbf{k}.
\end{align*}
Pinnan yksikkönormaali
on kohtisuorassa
näitä molempia tangenttivektoreita vastaan. Siksi se saadaan ristitulona
\begin{align*}
\mathbf{N} &= \mathbf{T}_1\times \mathbf{T}_2 =
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
1 & 0 & f_{x}(a,b) \\
0 & 1 & f_{y}(a,b)
\end{vmatrix}
=-f_{x}(a,b)\mathbf{i} - f_{y}(a,b)\mathbf{j} + \mathbf{k}.
\end{align*}
Pinnan yksikkönormaali  saadaan normaalista
saadaan normaalista  skaalaamalla sen pituudella:
skaalaamalla sen pituudella:
 sillä yllä olevan kaavan perusteella
sillä yllä olevan kaavan perusteella  ei voi olla nollavektori.
ei voi olla nollavektori.
Tangenttitaso
Olkoon  ,
,  ja
ja  .
Pinnan
.
Pinnan  tangenttitaso pisteessä
tangenttitaso pisteessä  on aina kohtisuorassa normaalia
on aina kohtisuorassa normaalia  vastaan
ja se kulkee pisteen
vastaan
ja se kulkee pisteen  kautta. Merkitään pisteen
kautta. Merkitään pisteen  paikkavektoria
paikkavektoria  .
Tällaisen tason vektorit
.
Tällaisen tason vektorit  toteuttavat yhtälön
toteuttavat yhtälön
 sillä tason suuntaiset vektorin ovat kohtisuorassa normaalia vastaan.
Tangenttitasolle saadaan siis yhtälö
sillä tason suuntaiset vektorin ovat kohtisuorassa normaalia vastaan.
Tangenttitasolle saadaan siis yhtälö

Normaalisuoran yhtälöt
Normaalisuora pinnalle  pisteessä
pisteessä  on normaalivektorin
on normaalivektorin
 suuntainen.
suuntainen.
Merkitään taas pisteen  paikkavektoria
paikkavektoria  . Tällöin normaalisuoran pisteet ovat pistejoukko
. Tällöin normaalisuoran pisteet ovat pistejoukko
 Jos sekä
Jos sekä  ja
ja  , niin voidaan eliminoida parametri
, niin voidaan eliminoida parametri  ja saadaan yhtälöt
ja saadaan yhtälöt

Esimerkki
Etsitään tangentti ja normaali pinnalle  , kun
, kun  ja
ja  .
Tangentti ja normaali kulkevat pisteen
.
Tangentti ja normaali kulkevat pisteen  kautta.
kautta.
Lasketaan osittaisderivaatat:
 Pisteessä
Pisteessä  saadaan
saadaan
 Siten kyseisellä pinnalla on normaalivektori
Siten kyseisellä pinnalla on normaalivektori
 Tangenttitaso on
Tangenttitaso on
 Ja normaalisuoran yhtälöiksi saadaan
Ja normaalisuoran yhtälöiksi saadaan

Kaltevuuskulma
Pinnan kaltevuuskulma mitataan vaakatasosta, mutta se on sama kuin pinnan ylänormaalin ja
yksikkövektorin
mitataan vaakatasosta, mutta se on sama kuin pinnan ylänormaalin ja
yksikkövektorin  välinen kulma: piirrä poikkileikkauskuva! Näin ollen
välinen kulma: piirrä poikkileikkauskuva! Näin ollen

2.3. Gradientti ja suunnattu derivaatta
Gradientti
Olkoon  ,
,  , derivoituva pisteessä
, derivoituva pisteessä  .
.
Määritelmä. Funktion  gradientti on vektori
gradientti on vektori
 Kaikki osittaisderivaatat lasketaan tutkittavassa pisteessä
Kaikki osittaisderivaatat lasketaan tutkittavassa pisteessä  .
.
Gradientti on tavallisen derivaatan oikea vastine usean muuttujan funktioille, koska se ottaa huomioon
kaikki osittaisderivaatat. Myöhemmin nähdään, että gradientti osoittaa siihen suuntaan, johon siirryttäessä
funktio  kasvaa nopeimmin, vrt. esimerkiksi termi "lämpötilagradientti".
Se on vektoriarvoinen funktio
kasvaa nopeimmin, vrt. esimerkiksi termi "lämpötilagradientti".
Se on vektoriarvoinen funktio  .
Tapauksessa
.
Tapauksessa  voidaan kirjoittaa
voidaan kirjoittaa
 Tapauksessa
Tapauksessa  kolmas termi jää pois. Gradientti on Jacobin matriisin erikoistapaus
kolmas termi jää pois. Gradientti on Jacobin matriisin erikoistapaus  , vrt. alla.
, vrt. alla.
Esimerkki
Olkoon  . Tällöin saadaan
. Tällöin saadaan  .
Erityisesti
.
Erityisesti  on kohtisuorassa origokeskisen (yksikkö)ympyrän mielivaltaiseen pisteeseen
on kohtisuorassa origokeskisen (yksikkö)ympyrän mielivaltaiseen pisteeseen  ) piirrettyä tangenttisuoraa vastaan.
Tämä on erikoistapaus yleisemmästä tasa-arvokäyriä koskevasta ominaisuudesta.
) piirrettyä tangenttisuoraa vastaan.
Tämä on erikoistapaus yleisemmästä tasa-arvokäyriä koskevasta ominaisuudesta.
Tasa-arvokäyrät
Olkoon  vakio,
vakio,  ja
ja  funktio.
Tällöin joukko
funktio.
Tällöin joukko  on usein tasokäyrä. Kyseinen pistejoukko voi olla myös tyhjä (jos
on usein tasokäyrä. Kyseinen pistejoukko voi olla myös tyhjä (jos  ei saa arvoa
ei saa arvoa  ) tai vaikkapa koko taso (jos
) tai vaikkapa koko taso (jos  on vakio).
Mikäli joukko
on vakio).
Mikäli joukko  on tasokäyrä, sitä sanotaan funktion
on tasokäyrä, sitä sanotaan funktion  arvoon
arvoon  liittyväksi tasa-arvokäyräksi.
liittyväksi tasa-arvokäyräksi.
Esimerkiksi korkeuskäyrät kartalla ovat tasa-arvokäyriä
funktiolle, joka liittää kartalla olevaan pisteeseen  sen korkeuden meren pinnasta.
sen korkeuden meren pinnasta.
Lause. Olkoon  ,
,  ja
ja  derivoituva
pisteessä
derivoituva
pisteessä  ja
ja  Tällöin
Tällöin  on kohtisuorassa pisteen
on kohtisuorassa pisteen  kautta kulkevaa
funktion
kautta kulkevaa
funktion  tasa-arvokäyrää (t.s., sen tangenttia) vasten.
tasa-arvokäyrää (t.s., sen tangenttia) vasten.
Seuraus: Jos piste  on funktion
on funktion  paikallinen
ääriarvo (minimi tai maksimi), niin
paikallinen
ääriarvo (minimi tai maksimi), niin  .
Gradientin nollakohta ei kuitenkaan välttämättä ole funktion ääriarvo.
Edes skalaarifunktion derivaatan nollakohta ei välttämättä ole minimi
eikä maksimi, kuten nähdään jos
.
Gradientin nollakohta ei kuitenkaan välttämättä ole funktion ääriarvo.
Edes skalaarifunktion derivaatan nollakohta ei välttämättä ole minimi
eikä maksimi, kuten nähdään jos  .
.
Todistus. Olkoon ![I = [-1,1] I = [-1,1]](https://mycourses.aalto.fi/filter/tex/pix.php/f0ca2e6cb7cc0e84726a5ef5509d1cac.gif) ja
ja  tasa-arvokäyrän sellainen parametrisointi,
että
tasa-arvokäyrän sellainen parametrisointi,
että  . Koska
. Koska  on tasa-arvokäyrä, kaikilla
on tasa-arvokäyrä, kaikilla  pätee
pätee  eli vakio.
Ketjusäännöstä saadaan (koska vakiofunktion derivaatta on nolla)
eli vakio.
Ketjusäännöstä saadaan (koska vakiofunktion derivaatta on nolla)
 Erityisesti pisteessä
Erityisesti pisteessä  tämä tarkoittaa, että
tämä tarkoittaa, että
 eli toisin sanoen vektori
eli toisin sanoen vektori  ja tangentin suuntainen
ja tangentin suuntainen  ovat kohtisuorassa.
ovat kohtisuorassa.
Suunnattu derivaatta
Edellinen tulos voidaan tulkita niin, että tasa-arvokäyrän tangentti antaa suunnan, johon edettäessä funktio ei kasva eikä vähene. Niinpä funktio kasvaa jyrkimmin gradienttinsa suuntaan, joka on tasa-arvokäyrän normaalivektori.
Muihin suuntiin liikuttessa kasvunopeuden antaa suunnattu derivaatta
 ja
ja  on yksikkösuuntavektori.
on yksikkösuuntavektori.
Lause. Olkoon  funktio,
funktio,  ja
ja  sellainen vektori, että
sellainen vektori, että  . Tällöin funktion
. Tällöin funktion  suunnattu derivaatta suuntaan
suunnattu derivaatta suuntaan  saadaan kaavasta
saadaan kaavasta

Esimerkki
Lasketaan

 a)
a)  ja siten
ja siten  . Saadaan
. Saadaan

Huomaa, että tässä  ja
ja  ovat yhdensuuntaiset.
ovat yhdensuuntaiset.
b)  ja siten
ja siten  . Saadaan
. Saadaan
 Vektorit
Vektorit  ja
ja  ovat siis kohtisuorassa.
ovat siis kohtisuorassa.
c)  ja siten
ja siten  . Saadaan
. Saadaan
 Tämä on sama kuin
Tämä on sama kuin  .
.
Määritelmä
Olkoon  ja
ja  vektori, missä
jokainen funktion
vektori, missä
jokainen funktion  komponentti on funktio
komponentti on funktio  ja
ja
 .
Tällainen vektori määrittelee vektoriarvoisen funktion
.
Tällainen vektori määrittelee vektoriarvoisen funktion  , jota kutsutaan myös vektorikentäksi.
Usein käytetään merkintää
, jota kutsutaan myös vektorikentäksi.
Usein käytetään merkintää  .
.
Vektoriarvoisia funktiota esiintyy usein mm. fysiikassa sellaisten suureiden yhteydessä, joilla on voimakkuus ja suunta (esimerkiksi nopeus- ja voimakentät).
Vektoriarvoisen funktion derivointi
Derivaatan luonnollinen vastine vektoriarvoisen funktion  tapauksessa on Jacobin matriisi
tapauksessa on Jacobin matriisi
 Jos
Jos  , Jacobin matriisi on neliömatriisi ja sen
determinattia sanotaan funktion
, Jacobin matriisi on neliömatriisi ja sen
determinattia sanotaan funktion  Jacobin determinantiksi
pisteessä
Jacobin determinantiksi
pisteessä  . Tätä determinanttia tarvitaan kurssin loppuosassa.
. Tätä determinanttia tarvitaan kurssin loppuosassa.
Jacobin matriiseilla ketjusääntö voidaan kirjoittaa yleisessä muodossa

Sovellus: implisiittifunktiolause
Oletetaan, että skalaarifunktiot  ovat derivoituvia. Tutkitaan yhtälöryhmää
ovat derivoituvia. Tutkitaan yhtälöryhmää
 pisteen
pisteen  lähellä.
Muuttujat
lähellä.
Muuttujat  voidaan esittää muuttujien
voidaan esittää muuttujien
 funktioina pisteen
funktioina pisteen  lähellä, jos
funktion
lähellä, jos
funktion  Jacobin
determinatti
Jacobin
determinatti

Esimerkki
Osoitetaan, että  voidaan esittää muuttujien
voidaan esittää muuttujien  funktiona systeemistä
funktiona systeemistä
 pisteen
pisteen  lähellä.
lähellä.
Selvästi  .
Muodostetaan Jacobin determinatti
.
Muodostetaan Jacobin determinatti
 Koska determinantti ei ole nolla,
voidaan kirjoittaa
Koska determinantti ei ole nolla,
voidaan kirjoittaa  kolmen muuttujan funktioina. Kaavoja näille funktioille ei kuitenkaan voida yleensä antaa.
kolmen muuttujan funktioina. Kaavoja näille funktioille ei kuitenkaan voida yleensä antaa.
2.4. Lineaarinen approksimaatio ja differentiaali
Approksimaatiot
Yksiulotteisessa tapauksessa muotoa  olevan funktion kuvaajan tangenttisuora
olevan funktion kuvaajan tangenttisuora  pisteessä
pisteessä  saadaan kaavasta
saadaan kaavasta
 Tangenttisuoran lauseke antaa myös tavan approksimoida funktiota
Tangenttisuoran lauseke antaa myös tavan approksimoida funktiota  pisteen
pisteen  läheisyydessä:
läheisyydessä:  .
.
Miksi approksimaatiota tarvitaan, jos kerran tietokone voi laskea nopeasti ja tarkasti?
Kun halutaan löytää "peukalosääntö" päässälaskun helpottamiseksi ja ymmärryksen lisäämiseksi.
Kun funktio  on olemassa ainoastaan taulukoituna, esimerkiksi
mittaustuloksista.
on olemassa ainoastaan taulukoituna, esimerkiksi
mittaustuloksista.
Lineaariset approksimaatiot usean muuttujan funktioille
Tapauksessa  saadaan funktiota
saadaan funktiota  approksimoiva tangenttitaso
approksimoiva tangenttitaso  , joka voidaan muodostaa osittaisderivaattojen avulla kaavasta
, joka voidaan muodostaa osittaisderivaattojen avulla kaavasta
 Kolmen muuttujan tapauksessa saadaan samannäköinen
approksimaatio
Kolmen muuttujan tapauksessa saadaan samannäköinen
approksimaatio

Esimerkki
Etsitään lineaarinen approksimaatio funktiolle
 pisteessä
pisteessä  , ja arvioidaan funktion arvoa pisteessä
, ja arvioidaan funktion arvoa pisteessä  .
.
Saadaan  . Funktion osittaisderivaatat ovat
. Funktion osittaisderivaatat ovat
 ja
ja
 Siten
Siten
 Haluttu approksimaatio siis on
Haluttu approksimaatio siis on
 Vertailun vuoksi funktion
Vertailun vuoksi funktion  todellinen arvo pisteessä
todellinen arvo pisteessä  on noin
on noin  .
.
Differentiaali
Lineaarisen approksimaation lauseketta kutsutaan funktion differentiaaliksi (tai kokonaisdifferentiaaliksi) ja se voidaan kirjoittaa kahden muuttujan tapauksessa muodossa
 Differentiaalia merkitään
Differentiaalia merkitään  . Tarkasti ottaen merkintään liittyy sekä tutkittava piste että siirtymävektori.
. Tarkasti ottaen merkintään liittyy sekä tutkittava piste että siirtymävektori.
 on jatkuvat osittaisderivaatat, niin differentiaaliin liittyvä virhetermi voidaan esittää muodossa
on jatkuvat osittaisderivaatat, niin differentiaaliin liittyvä virhetermi voidaan esittää muodossa  , jossa
, jossa  , kun
, kun  .
Tässä siis
.
Tässä siis  ja
ja  . Yleinen differentiaalikaava
. Yleinen differentiaalikaava  -ulotteisessa tapauksessa on muotoa
-ulotteisessa tapauksessa on muotoa
 Makroskooppisen virheen arviointiin voidaan käyttää approksimaatiota
Makroskooppisen virheen arviointiin voidaan käyttää approksimaatiota
 jossa viimeinen muoto koskee tapausta
jossa viimeinen muoto koskee tapausta  . Tässä merkintä
. Tässä merkintä  viittaa siihen, että epäyhtälö
viittaa siihen, että epäyhtälö  ei tarkasti ottaen ole voimassa, koska virhetermi on jätetty pois.
ei tarkasti ottaen ole voimassa, koska virhetermi on jätetty pois.
Huomautuksia
Toisin kuin yksiulotteisessa tapauksessa pelkkä osittaisderivaattojen olemassaolo ei riitä takaamaan edes funktion  jatkuvuutta.
Esimerkiksi funktiolle
jatkuvuutta.
Esimerkiksi funktiolle
 on
on  , mutta funktio on epäjatkuva pisteessä
, mutta funktio on epäjatkuva pisteessä  .
Toinen samanlainen esimerkki on funktio
.
Toinen samanlainen esimerkki on funktio
 Siksi tilannetta on tarpeen analysoida tarkemmin. Halutaan ehto,
joka kertoo milloin lineaarinen approksimaatio on mielekäs funktiolle
Siksi tilannetta on tarpeen analysoida tarkemmin. Halutaan ehto,
joka kertoo milloin lineaarinen approksimaatio on mielekäs funktiolle  lähellä pistettä
lähellä pistettä  .
.
Differentioituvuus
Määritelmä. Funktio  on differentioituva pisteessä
on differentioituva pisteessä  , jos
, jos

Differentiaalikaavan avulla (virhetermi mukana!) voidaan todistaa seuraava tulos:
Lause. Jos  ovat jatkuvia jossakin pisteen
ovat jatkuvia jossakin pisteen  ympäristössä, niin
ympäristössä, niin  on differentioituva pisteessä
on differentioituva pisteessä  .
.
Esimerkki
Osittaisderivaatoiksi saadaan  ja
ja  , joten
\begin{align*}
&f(x+h,y+k)-f(x,y)-h\,f_{x}(x,y)-k\,f_{y}(x,y) \\
&\quad =(x+h)^3+(x+h)(y+k)^2-x^3-xy^2-(3x^2+y^2)h -2xyk\\
&\quad=3xh^2+h^3+2yhk+hk^2+xk^2. \\
\end{align*}
Lausekeen
, joten
\begin{align*}
&f(x+h,y+k)-f(x,y)-h\,f_{x}(x,y)-k\,f_{y}(x,y) \\
&\quad =(x+h)^3+(x+h)(y+k)^2-x^3-xy^2-(3x^2+y^2)h -2xyk\\
&\quad=3xh^2+h^3+2yhk+hk^2+xk^2. \\
\end{align*}
Lausekeen  - ja
- ja  -termit lähestyvät nollaa vähintään samalla nopeudella kuin
-termit lähestyvät nollaa vähintään samalla nopeudella kuin  , kun
, kun  , joten differentioituvuuden
määritelmä selvästi toteutuu.
, joten differentioituvuuden
määritelmä selvästi toteutuu.
2.5. Ketjusäännöt ja lineaarinen approksimointi
Motivaatio
Yleistetään derivoinnin ketjusääntö
 usean muuttujan funktioille
usean muuttujan funktioille  .
.
Ketjusääntö liittyy suoraan myös moniin käytännön sovelluksiin. Voidaan ajatella fysikaalista suuretta kuten lämpötilaa tai mekaanisen systeemin kokonaisenergiaa, jotka riippuvat useista eri toissijaisista muuttujista (kuten ajasta, paikasta tai nopeudesta). Nämä muuttujat voivat riippua edelleen kolmansista muuttujista (paikka ja nopeus esimerkiksi ajasta). Halutaan tarkastella kiinnostavan fysikaalisen suureen muutosnopeutta mainittujen kolmansien muuttujien suhteen.
Esimerkki
Retkeilijä liikkuu karttaa käyttäen mäkisessä maastossa. Olkoon  retkeilijän paikka kartalla,
retkeilijän paikka kartalla,  kulloinenkin korkeus meren pinnasta ja
kulloinenkin korkeus meren pinnasta ja
 retkeilijän paikka kartalla hetkellä
retkeilijän paikka kartalla hetkellä  .
Retkeilijän paikan korkeus eli etäisyys meren pinnan tasosta hetkellä
.
Retkeilijän paikan korkeus eli etäisyys meren pinnan tasosta hetkellä  on siis yhdistetty funktio
on siis yhdistetty funktio
 Kuinka nopeasti retkelijän paikan korkeus muuttuu ajan kuluessa?
Kuinka nopeasti retkelijän paikan korkeus muuttuu ajan kuluessa?
Ilmeisestikin vastaus kysymykseen on funktion  derivaatta. Lasketaan:
\begin{align*}
\lim_{h\to 0}\frac{g(t+h)-g(t)}{h}
&= \lim_{h\to 0}\frac{f(u(t+h),v(t+h))-f(u(t),v(t))}{h} \\
&= \lim_{h\to 0}\frac{f(u(t+h),v(t+h))-f(u(t),v(t+h))}{h}\\
&\quad + \lim_{h\to 0}\frac{f(u(t),v(t+h))-f(u(t),v(t))}{h}
\end{align*}
Yhden muuttujan ketjusäännön perusteella
derivaatta. Lasketaan:
\begin{align*}
\lim_{h\to 0}\frac{g(t+h)-g(t)}{h}
&= \lim_{h\to 0}\frac{f(u(t+h),v(t+h))-f(u(t),v(t))}{h} \\
&= \lim_{h\to 0}\frac{f(u(t+h),v(t+h))-f(u(t),v(t+h))}{h}\\
&\quad + \lim_{h\to 0}\frac{f(u(t),v(t+h))-f(u(t),v(t))}{h}
\end{align*}
Yhden muuttujan ketjusäännön perusteella

Ketjusäännöt
Olkoon  muuttujien
muuttujien  jatkuvasti derivoituva funktio (eli funktio, jolla on jatkuvat 1. kertaluvun osittaisderivaatat).
Jos
jatkuvasti derivoituva funktio (eli funktio, jolla on jatkuvat 1. kertaluvun osittaisderivaatat).
Jos  ovat muuttujan
ovat muuttujan  jatkuvasti derivoituvia funktioita, niin
jatkuvasti derivoituvia funktioita, niin
 Jos
Jos  ovat kahden muuttujan
ovat kahden muuttujan  jatkuvasti derivoituvia funktioita, niin
\begin{equation}
\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial s}
+ \frac{\partial z}{\partial y}\frac{\partial y}{\partial s}
\end{equation}
ja
\begin{equation}
\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial t}
+ \frac{\partial z}{\partial y}\frac{\partial y}{\partial t}.
\end{equation}
jatkuvasti derivoituvia funktioita, niin
\begin{equation}
\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial s}
+ \frac{\partial z}{\partial y}\frac{\partial y}{\partial s}
\end{equation}
ja
\begin{equation}
\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial t}
+ \frac{\partial z}{\partial y}\frac{\partial y}{\partial t}.
\end{equation}
Ketjusäännöt voidaan todistaa soveltamalla tutkittavaan erotusosamäärään lineaarisen approksimaation kaavoja virhetermeineen.
Huom. Derivaatan ketjusääntö voidaan kirjoittaa myös gradientin avulla: Jos  , niin
, niin

Keskeisiä kysymyksiä:
Mikä on yleinen idea näissä kaavoissa?
Kuinka voidaan muodostaa yleisessä tapauksessa laskentakaava yhdistetyn funktion (osittais)derivaatoille?
Ajatellaanpa, että  , jossa
, jossa  ja
ja  . Tarkastellaan graafina "infinitesimaalisen muutoksen etenemistä"
muuttujasta
. Tarkastellaan graafina "infinitesimaalisen muutoksen etenemistä"
muuttujasta  muuttujaan
muuttujaan  kaikkien etenemisreittien kautta.
kaikkien etenemisreittien kautta.
Kuinka tilanne muuttuu, jos lisäksi  ja
ja  jolloin
jolloin  ja kysytään kaavaa derivaatalle
ja kysytään kaavaa derivaatalle  ?
Saadaan
?
Saadaan
 ja
\begin{align*}
\frac{d z}{d t} & = \frac{\partial f}{\partial u} \left ( \frac{\partial u}{\partial x} \frac{d x}{d t} + \frac{\partial u}{\partial y} \frac{d y}{d t} \right ) \\
&\quad+ \frac{\partial f}{\partial v} \left ( \frac{\partial v }{\partial t} + \frac{\partial v}{\partial y} \frac{d y}{d t} \right ) + \frac{\partial f}{\partial t},
\end{align*}
jossa on yhteensä viisi termiä.
ja
\begin{align*}
\frac{d z}{d t} & = \frac{\partial f}{\partial u} \left ( \frac{\partial u}{\partial x} \frac{d x}{d t} + \frac{\partial u}{\partial y} \frac{d y}{d t} \right ) \\
&\quad+ \frac{\partial f}{\partial v} \left ( \frac{\partial v }{\partial t} + \frac{\partial v}{\partial y} \frac{d y}{d t} \right ) + \frac{\partial f}{\partial t},
\end{align*}
jossa on yhteensä viisi termiä.
Esimerkki
Olkoon  jatkuvasti derivoituva. Etsitään
jatkuvasti derivoituva. Etsitään

Saadaan \begin{align*} \frac{\partial}{\partial x} f(x^2y,x+2y) &= f_{x}(x^2y,x+2y)\frac{\partial}{\partial x} (x^2y) \\ &\quad +f_{y}(x^2y,x+2y)\frac{\partial}{\partial x}(x+2y) \\ &= 2xy f_{x}(x^2y,x+2y)+ f_{y}(x^2y,x+2y). \end{align*} Vastaavasti voidaan laskea \begin{align*} \frac{\partial}{\partial y} f(x^2y,x+2y) &= f_{x}(x^2y,x+2y)\frac{\partial}{\partial y} (x^2y) \\ & +f_{y}(x^2y,x+2y)\frac{\partial}{\partial y}(x+2y) \\ &= x^2 f_{x}(x^2y,x+2y)+ 2f_{y}(x^2y,x+2y). \end{align*}
Esimerkki
Lämpötila ilmakehässä C) riippuu paikasta
C) riippuu paikasta  sekä ajasta
sekä ajasta  . Ajatellaan lämpötilaa näistä parametrista riippuvana funktiona
. Ajatellaan lämpötilaa näistä parametrista riippuvana funktiona  .
Jos funktio
.
Jos funktio  esittää sääpalloon liitetyn lämpömittarin mittaamaa lämpötilaa, määritetään
esittää sääpalloon liitetyn lämpömittarin mittaamaa lämpötilaa, määritetään  :n muutos ajan suhteen.
:n muutos ajan suhteen.
Määritetään lämpötilan muutos hetkellä  , kun
, kun
 ja sääpallo etenee reittiä
ja sääpallo etenee reittiä  .
Koska lämpömittarin lukeman muutos riippuu kaikista neljästä parametrista, mitään niistä ei voida jättää huomiotta.
.
Koska lämpömittarin lukeman muutos riippuu kaikista neljästä parametrista, mitään niistä ei voida jättää huomiotta.
Lämpötilan muutoksen kaavaksi saadaan siten
 Koordinaattifunktioiden arvot hetkellä
Koordinaattifunktioiden arvot hetkellä  ovat
ovat
 Koordinaattifunktioiden derivaattojen arvot hetkellä
Koordinaattifunktioiden derivaattojen arvot hetkellä  ovat
ovat
 Siten hetkellä
Siten hetkellä  saadaan
\begin{align*}
\frac{\partial T}{\partial x} &= \frac{y}{1+z}(1+t)=4,
&&\frac{\partial T}{\partial y} = \frac{x}{1+z}(1+t)=2, \\
\frac{\partial T}{\partial z} &= \frac{-xy}{(1+z)^2}(1+t)=-4,
&&\frac{\partial T}{\partial t} = \frac{xy}{1+z}=2.
\end{align*}
Näin ollen,
saadaan
\begin{align*}
\frac{\partial T}{\partial x} &= \frac{y}{1+z}(1+t)=4,
&&\frac{\partial T}{\partial y} = \frac{x}{1+z}(1+t)=2, \\
\frac{\partial T}{\partial z} &= \frac{-xy}{(1+z)^2}(1+t)=-4,
&&\frac{\partial T}{\partial t} = \frac{xy}{1+z}=2.
\end{align*}
Näin ollen,

3. Taylorin polynomi ja sarja
Taylorin kaava
Yhden muuttujan tapauksessa  kertaa jatkuvasti derivoituvaa funktiota
kertaa jatkuvasti derivoituvaa funktiota  voidaan approksimoida kaavalla
voidaan approksimoida kaavalla
 kun
kun  .
.
Tämä idea yleistyy usean muuttujan tapaukseen: Jos  ,
,  ja funktiolla
ja funktiolla  on
jatkuvat kertaluvun
on
jatkuvat kertaluvun  osittaisderivaatat pisteitä
osittaisderivaatat pisteitä
 yhdistävällä janalla, niin
yhdistävällä janalla, niin

Perustelu. Yksinkertaisuuden vuoksi johdetaan tässä kaava tapauksessa  riittävän sileille funktioille.
Olkoon
riittävän sileille funktioille.
Olkoon  avoin ja funktio
avoin ja funktio
 äärettömän monta kertaa jatkuvasti derivoituva.
Lisäksi oletetaan, että
äärettömän monta kertaa jatkuvasti derivoituva.
Lisäksi oletetaan, että  , kun
, kun  . Tällöin oleellisesti myös apufunktion
. Tällöin oleellisesti myös apufunktion
 kaikki derivaatat ovat jatkuvia suljetulla välillä
kaikki derivaatat ovat jatkuvia suljetulla välillä ![\left[0,1\right] \left[0,1\right]](https://mycourses.aalto.fi/filter/tex/pix.php/4f27db35c23e1b587a92f6ba055a4b94.gif) .
.
Ketjusäännön nojalla saadaan apufunktiota derivoimalla



 Tästä havaitaan, että
Tästä havaitaan, että  ja siten yhden muuttujan funktion
ja siten yhden muuttujan funktion  Taylorin sarjakehitelmä on
muotoa
Taylorin sarjakehitelmä on
muotoa
 Asettamalla tässä
Asettamalla tässä  saadaan haluttu tulos,
saadaan haluttu tulos,


Esimerkki
Olkoon  ja
ja  neljä kertaa jatkuvasti derivoituva kiekossa
neljä kertaa jatkuvasti derivoituva kiekossa  -keskisessä
-keskisessä  -säteisessä kiekossa.
Etsitään 3. asteen approksimaatio. Jos
-säteisessä kiekossa.
Etsitään 3. asteen approksimaatio. Jos  , niin
\begin{align*}
f(a+h,b+k)&\approx
f(a,b) + (hD_1+kD_2)f(a,b) +\frac{1}{2!}(hD_1+kD_2)^2f(a,b) \\
&\quad +\frac{1}{3!}(hD_1+kD_2)^3f(a,b) \\
&= f(a,b) + hf_{x}(a,b)+kf_{y}(a,b) \\
&\quad+ \frac{1}{2!}\Big(h^2f_{xx}(a,b)+2hkf_{xy}(a,b)+k^2f_{yy}(a,b)\Big) \\
&\quad+\frac{1}{3!}\Big(h^3f_{xxx}(a,b)+ 3h^2kf_{xxy}(a,b)+3hk^2f_{xyy}(a,b)+k^3f_{yyy}(a,b)\Big).
\end{align*}
, niin
\begin{align*}
f(a+h,b+k)&\approx
f(a,b) + (hD_1+kD_2)f(a,b) +\frac{1}{2!}(hD_1+kD_2)^2f(a,b) \\
&\quad +\frac{1}{3!}(hD_1+kD_2)^3f(a,b) \\
&= f(a,b) + hf_{x}(a,b)+kf_{y}(a,b) \\
&\quad+ \frac{1}{2!}\Big(h^2f_{xx}(a,b)+2hkf_{xy}(a,b)+k^2f_{yy}(a,b)\Big) \\
&\quad+\frac{1}{3!}\Big(h^3f_{xxx}(a,b)+ 3h^2kf_{xxy}(a,b)+3hk^2f_{xyy}(a,b)+k^3f_{yyy}(a,b)\Big).
\end{align*}
Huom. 1. asteen Taylor-approksimaatio on sama kuin tangenttitaso.
Esimerkki
Etsitään 2. asteen Taylor-approksimaatio funktiolle  pisteen
pisteen  ympäristössä.
ympäristössä.
Lasketaan  ,
,
 eli
eli  ja
ja  .
Edelleen
.
Edelleen


 Siten
\begin{align*}
f(1+h,2+k) &\approx 3 + \frac{1}{3}h + 2k +
\frac{1}{2!}\Big(\frac{8}{27}h^2+2\Big(-\frac{2}{9}\Big)hk+\frac{2}{3}k^2\Big) \\
&= \frac{4}{27}h^2-\frac{2}{9}hk+\frac{1}{3}k^2+\frac{1}{3}h + 2k + 3.
\end{align*}
Siten
\begin{align*}
f(1+h,2+k) &\approx 3 + \frac{1}{3}h + 2k +
\frac{1}{2!}\Big(\frac{8}{27}h^2+2\Big(-\frac{2}{9}\Big)hk+\frac{2}{3}k^2\Big) \\
&= \frac{4}{27}h^2-\frac{2}{9}hk+\frac{1}{3}k^2+\frac{1}{3}h + 2k + 3.
\end{align*}
4. Ääriarvot
Kertausta: ääriarvot yhden muuttujan tapauksessa
Funktiolla on lokaali (paikallinen) maksimi pisteessä
on lokaali (paikallinen) maksimi pisteessä  , jos
, jos  kaikilla
kaikilla  :n arvoilla jossakin
:n arvoilla jossakin  :n ympäristössä (eli riittävän lähellä pistettä
:n ympäristössä (eli riittävän lähellä pistettä  ). Vastaavasti lokaali minimi tarkoittaa sitä, että
). Vastaavasti lokaali minimi tarkoittaa sitä, että  jossakin
jossakin  :n ympäristössä. Maksimi tai minimi on globaali, jos kyseinen epäyhtälö on voimassa kaikilla
:n ympäristössä. Maksimi tai minimi on globaali, jos kyseinen epäyhtälö on voimassa kaikilla  .
. Ääriarvoja voi esiintyä:
Seuraavaksi yleistetään vastaavat ehdot funktion  tapaukseen.
tapaukseen.
Ääriarvot ja usean muuttujan funktiot
Funktiolla on pisteessä
on pisteessä  lokaali maksimi, jos jossakin pisteen
lokaali maksimi, jos jossakin pisteen  ympäristössä
ympäristössä  pätee
pätee  kaikilla
kaikilla  . Vastaavasti
. Vastaavasti  on pisteessä
on pisteessä  lokaali minimi, jos löytyy sellainen pisteen
lokaali minimi, jos löytyy sellainen pisteen  ympäristö
ympäristö  , että
, että  kaikilla
kaikilla  . Ääriarvo on globaali eli absoluuttinen, jos kyseinen epäyhtälö on voimassa kaikilla
. Ääriarvo on globaali eli absoluuttinen, jos kyseinen epäyhtälö on voimassa kaikilla  .
. Ääriarvoja voi esiintyä:
 kriittistä pistettä
kriittistä pistettä  , joka ei ole maksimi tai minimi, kutsutaan funktion
, joka ei ole maksimi tai minimi, kutsutaan funktion  satulapisteeksi.
satulapisteeksi.
Esimerkki
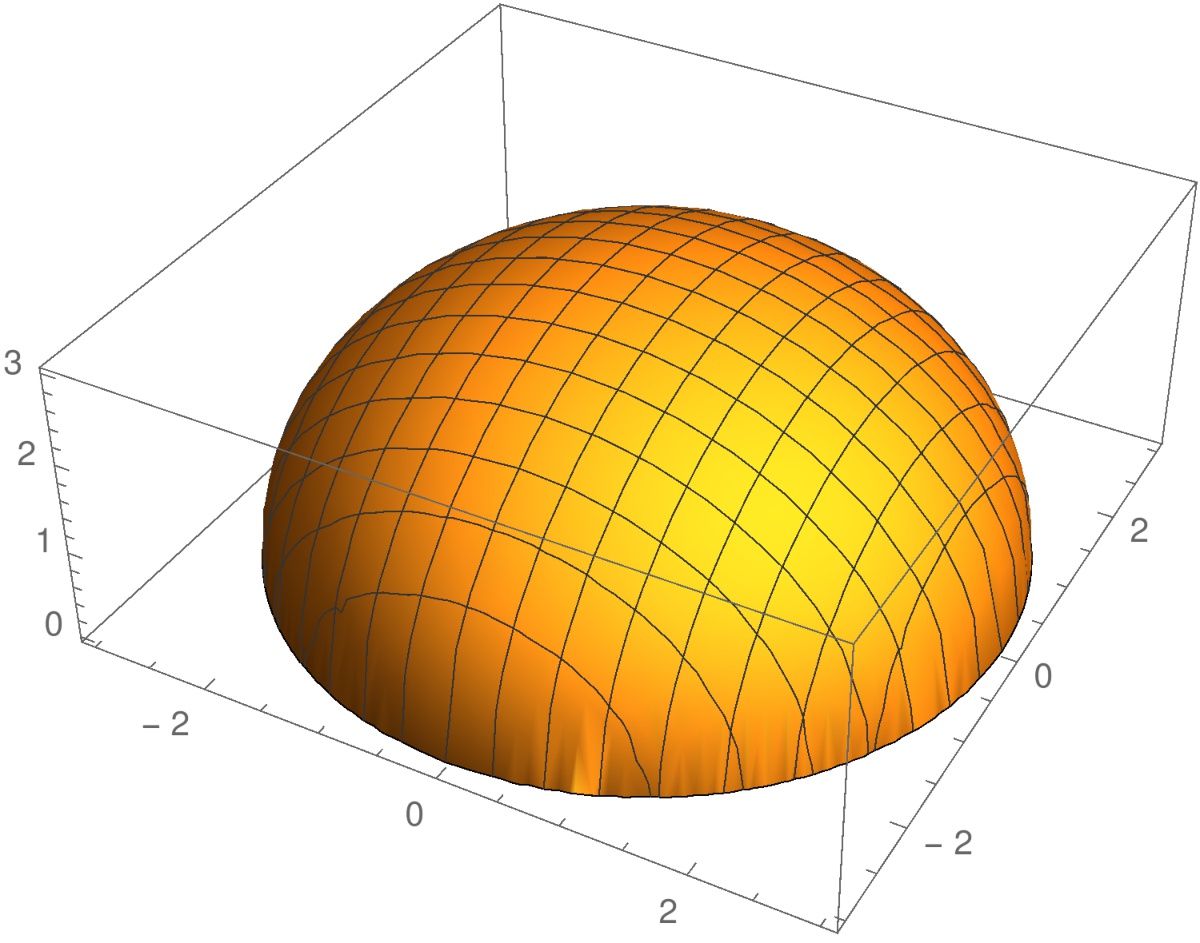
Funktiolla  on globaali maksimi
on globaali maksimi  pisteessä
pisteessä  . Tämä piste on funktion
. Tämä piste on funktion  kriittinen piste, koska
kriittinen piste, koska 
Esimerkki
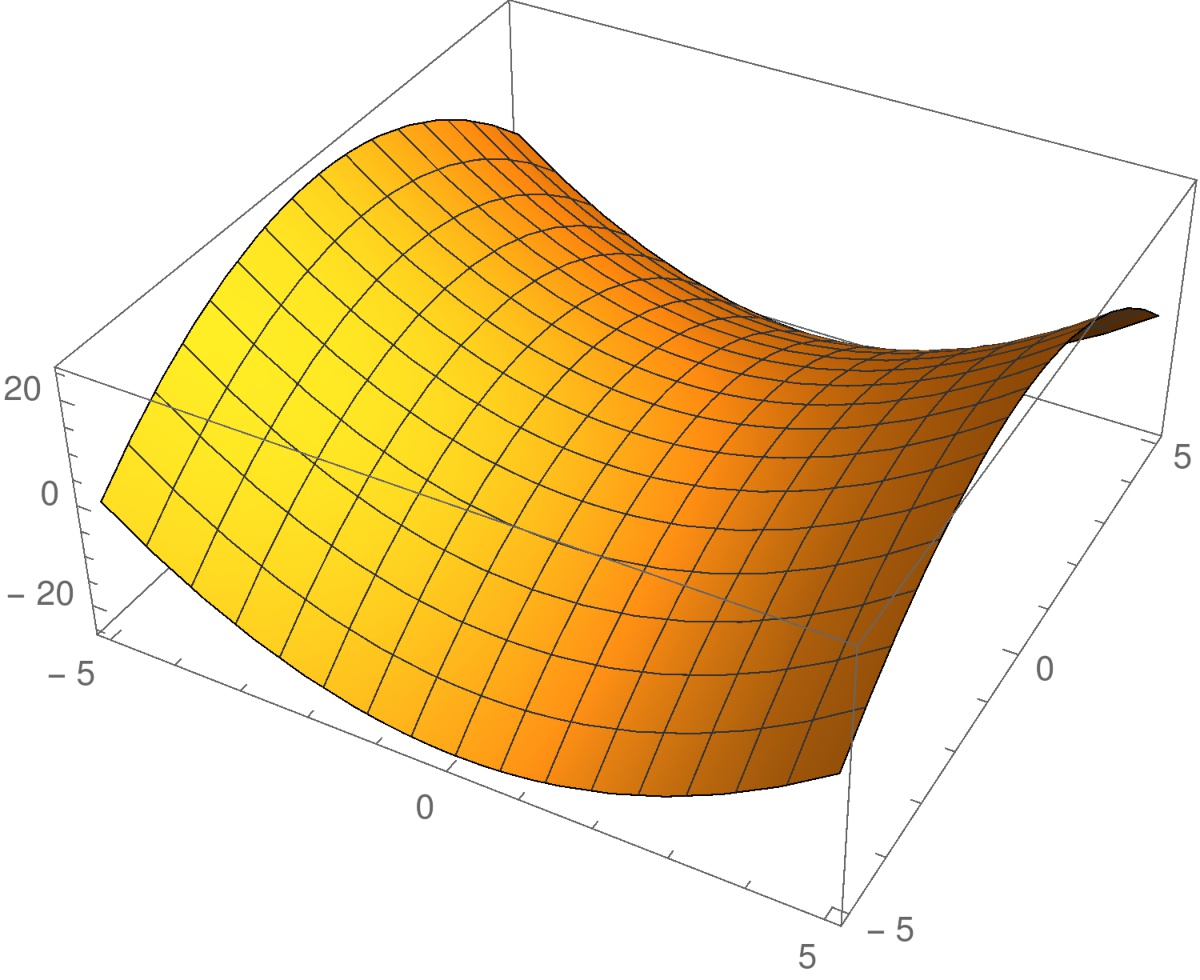
 on satulapiste
on satulapiste  . Tämä piste on funktion
. Tämä piste on funktion  kriittinen piste, koska
kriittinen piste, koska 
Esimerkki
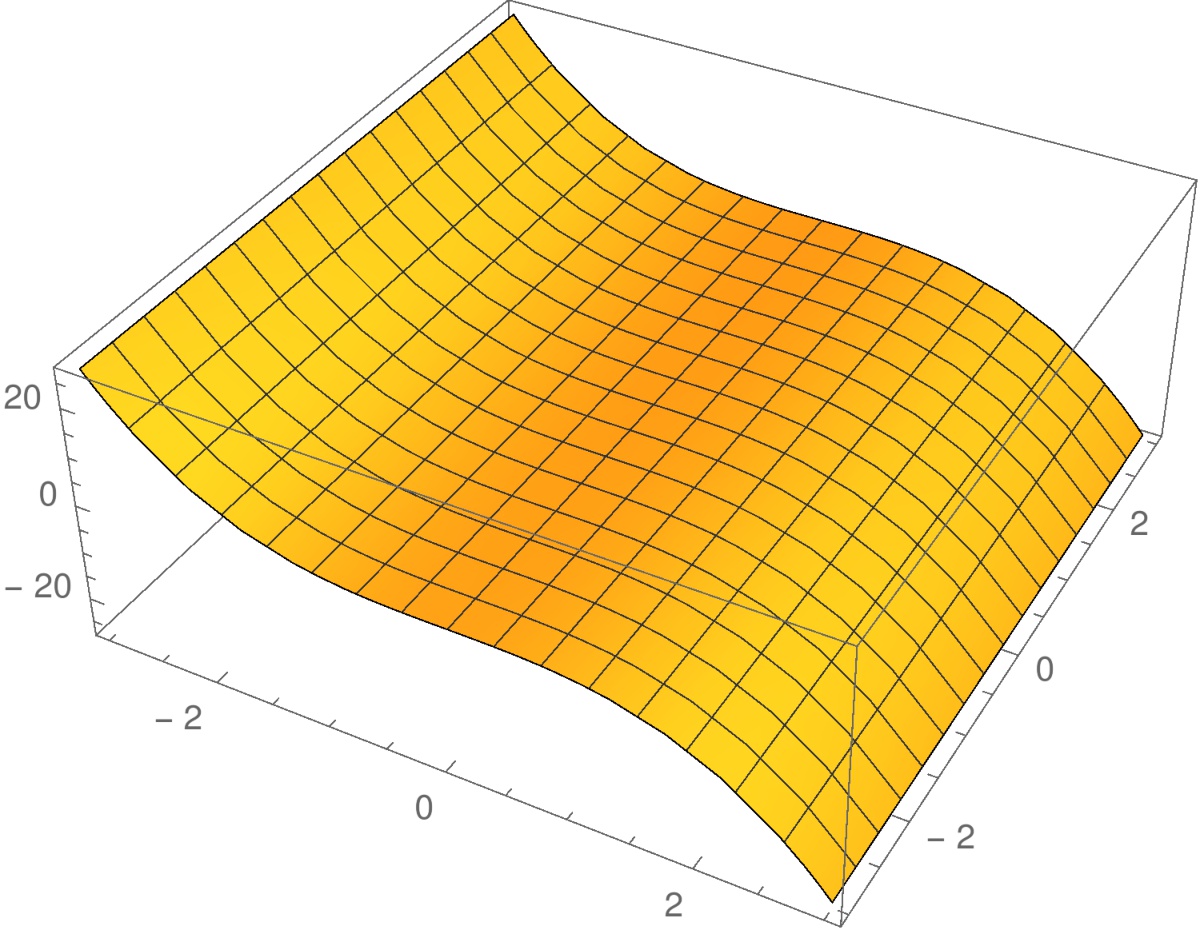
 ovat funktion
ovat funktion  satulapisteitä. Huomaa, että
satulapisteitä. Huomaa, että 
Esimerkki
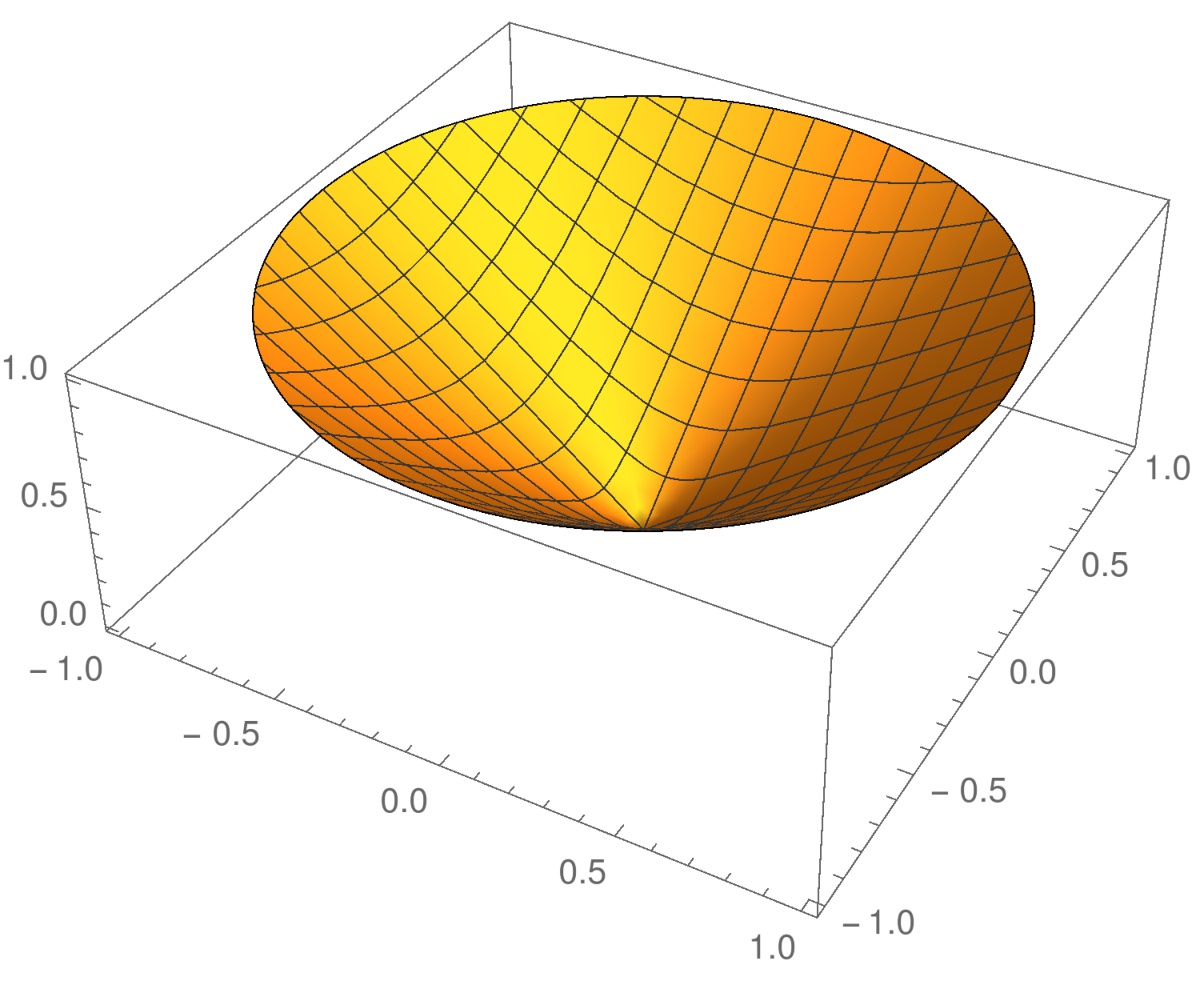
 on lokaali minimi
on lokaali minimi  pisteessä
pisteessä  . Funktio
. Funktio  on jatkuva, mutta sen gradientti
on jatkuva, mutta sen gradientti  ei ole määritelty tässä pisteessä.
ei ole määritelty tässä pisteessä.
Esimerkki
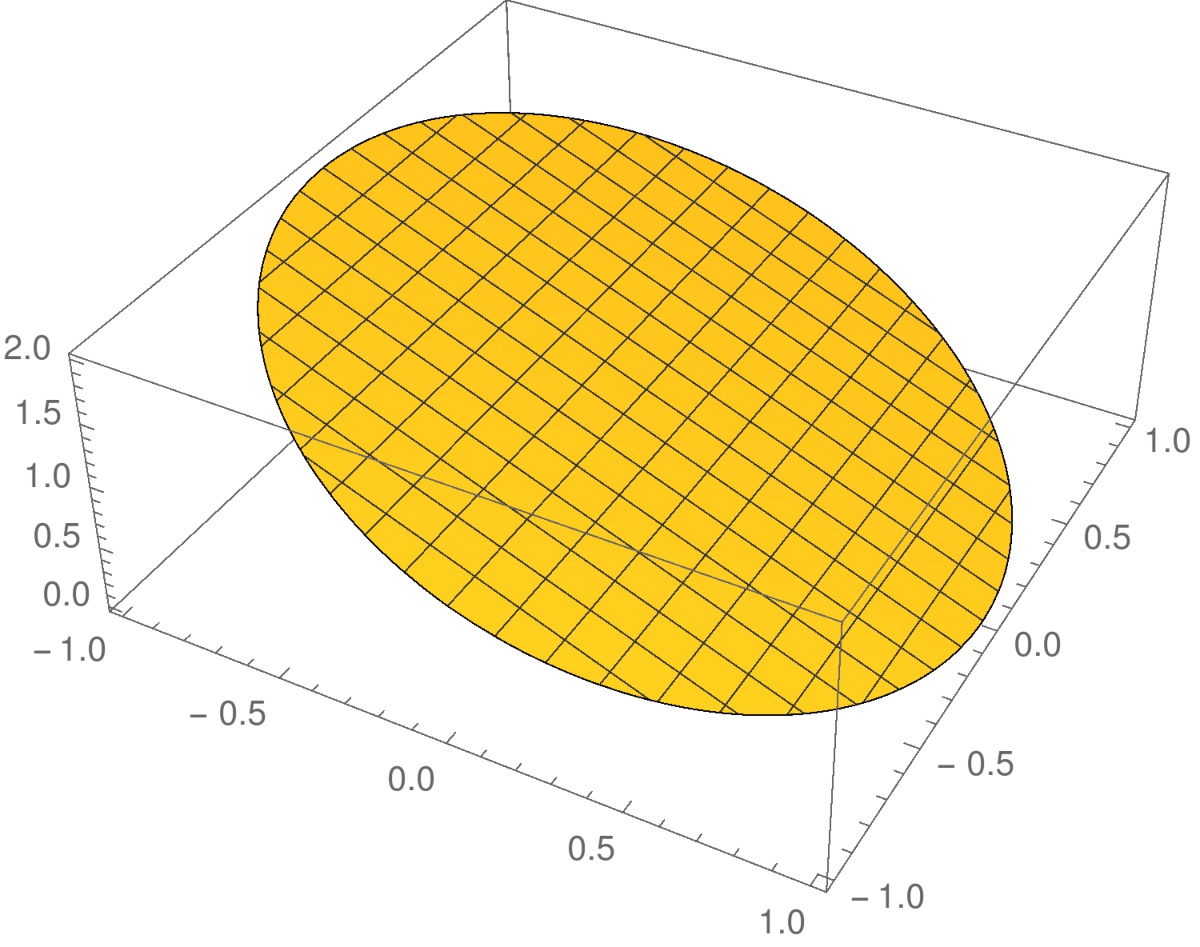
 ei ole paikallisia ääriarvoja, jos sen määrittelyjoukko on koko taso
ei ole paikallisia ääriarvoja, jos sen määrittelyjoukko on koko taso  . Jos määrittelyjoukoksi kuitenkin ajatellaan esimerkiksi kiekko
. Jos määrittelyjoukoksi kuitenkin ajatellaan esimerkiksi kiekko  , niin sen reunalla saadaan maksimi
, niin sen reunalla saadaan maksimi  ja minimi
ja minimi  .
.
4.1. Kriittisten pisteiden luokittelu
Johdanto
Ääriarvojen luokittelu perustuu suureen  tarkasteluun kriittisessä pisteessä
tarkasteluun kriittisessä pisteessä  . Jos
. Jos  saa vain positiivisia arvoja (kun
saa vain positiivisia arvoja (kun  on pieni), on piste
on pieni), on piste  minimi ja negatiivisessa tapauksessa maksimi. Jos
minimi ja negatiivisessa tapauksessa maksimi. Jos  vaihtaa merkkiä, niin piste
vaihtaa merkkiä, niin piste  ei ole minimi eikä maksimi. Tämä johtaa funktion
ei ole minimi eikä maksimi. Tämä johtaa funktion  toisen derivaatan tarkasteluun kriittisessä pisteessä.
toisen derivaatan tarkasteluun kriittisessä pisteessä.
Yhden muuttujan tapauksessa:
Hessen matriisi
Olkoon funktio, jolla on jatkuvat toisen kertaluvun osittaisderivaatat. Funktion
funktio, jolla on jatkuvat toisen kertaluvun osittaisderivaatat. Funktion  luonnollinen derivaattakäsite on gradientti, joka itsessään on vektoriarvoinen funktio
luonnollinen derivaattakäsite on gradientti, joka itsessään on vektoriarvoinen funktio  . Siten funktion
. Siten funktion  toinen derivaatta on matriisi, jota nimitetään Hessen matriisiksi
toinen derivaatta on matriisi, jota nimitetään Hessen matriisiksi  Koska
Koska  on kaksi kertaa jatkuvasti derivoituva, derivoinnin järjestystä voidaan vaihtaa, ja kyseinen matriisi on symmetrinen.
on kaksi kertaa jatkuvasti derivoituva, derivoinnin järjestystä voidaan vaihtaa, ja kyseinen matriisi on symmetrinen.
Miksi Hessen matriisi kiinnostaa meitä? Kun gradientin avulla voidaan kirjoittaa lineaarinen (ensimmäisen asteen) approksimaatio funktiolle  , niin Hessen matriisilla saadaan kvadraattinen tarkennus:
, niin Hessen matriisilla saadaan kvadraattinen tarkennus:  jossa (vaaka)vektori
jossa (vaaka)vektori  on pieni.
on pieni.
Tämä kaava on itse asiassa ainoastaan uusi tapa kirjoittaa toisen kertaluvun Taylorin approksimaatio  :n muuttujan funktiolle. Muotoa
:n muuttujan funktiolle. Muotoa  oleva lauseke on
oleva lauseke on  -neliömatriisille
-neliömatriisille  niin kutsuttu neliömuoto, jossa
niin kutsuttu neliömuoto, jossa  on
on  -pystyvektori.
-pystyvektori.
Kirjoita kaava auki tapauksessa  !
!
Pisteessä, jossa  , on voimassa approksimaatio
, on voimassa approksimaatio  Tätä voidaan käyttää hyväksi mahdollisen ääriarvon luokittelussa pisteessä
Tätä voidaan käyttää hyväksi mahdollisen ääriarvon luokittelussa pisteessä  ajattelemalla, että
ajattelemalla, että  .
.
Matriisin (ja neliömuodon) definiittisyys
Symmetristä  -matriisia
-matriisia  sanotaan positiividefiniitiksi, jos sen kaikki ominaisarvot ovat positiivisia ja negatiividefiniitiksi, jos
sanotaan positiividefiniitiksi, jos sen kaikki ominaisarvot ovat positiivisia ja negatiividefiniitiksi, jos  on positiividefiniitti. Matriisin sanotaan olevan indefiniitti, jos sen kaikki ominaisarvot ovat nollasta poikkeavia ja sillä on vähintään yksi positiivinen sekä yksi negatiivinen ominaisarvo. Positiivi/negatiividefiniiteillä matriiseilla on monia samoja ominaisuuksia kuin positiivisilla/negatiivisilla reaaliluvuilla.
on positiividefiniitti. Matriisin sanotaan olevan indefiniitti, jos sen kaikki ominaisarvot ovat nollasta poikkeavia ja sillä on vähintään yksi positiivinen sekä yksi negatiivinen ominaisarvo. Positiivi/negatiividefiniiteillä matriiseilla on monia samoja ominaisuuksia kuin positiivisilla/negatiivisilla reaaliluvuilla.
Symmetrisen matriisin  definiittiys tai indefiniittiys periytyy sitä vastaavalle neliömuodolle.
definiittiys tai indefiniittiys periytyy sitä vastaavalle neliömuodolle.
 on positiividefiniitti
on positiividefiniitti 
 kaikilla nollasta poikkeavilla pystyvektoreilla
kaikilla nollasta poikkeavilla pystyvektoreilla  .
.
 on negatiividefiniitti
on negatiividefiniitti 
 kaikilla nollasta poikkeavilla pystyvektoreilla
kaikilla nollasta poikkeavilla pystyvektoreilla  .
.
 on indefiniitti
on indefiniitti 
 saavuttaa sekä negatiivisia että positiivisia arvoja pystyvektorin
saavuttaa sekä negatiivisia että positiivisia arvoja pystyvektorin  vaihdellessa.
vaihdellessa.
 muotoon
muotoon  , jossa diagonaalimatriisi
, jossa diagonaalimatriisi  sisältää
sisältää  :n ominaisarvot.
:n ominaisarvot.
Toisen derivaatan testi monen muuttajan tapauksessa
Lause. Olkoon funktio, jolla on jatkuvat toisen kertaluvun osittaisderivaatat kriittisen pisteen
funktio, jolla on jatkuvat toisen kertaluvun osittaisderivaatat kriittisen pisteen  ympäristössä. Tällöin:
ympäristössä. Tällöin:
Lause seuraa approksimaatiosta  kun
kun  . Väite täytyy nimittäin ainoastaan tarkastaa Hessen matriisin määräämälle neliömuodolle.
. Väite täytyy nimittäin ainoastaan tarkastaa Hessen matriisin määräämälle neliömuodolle.
Esimerkki
Etsitään ja luokitellaan funktion  kriittiset pisteet.
kriittiset pisteet.
Yhtälöt kriittisille pisteille ovat \begin{align*} 0 &= f_{x}(x,y,z)=2xy-2,\\ 0 &= f_{y}(x,y,z)=x^2+2yz,\\ 0 &= f_{z}(x,y,z)=y^2+2z.\\ \end{align*} Nämä yhtälöt ratkaisemalla nähdään, että funktion  ainoa kriittinen piste on
ainoa kriittinen piste on  .
.
Lasketaan Hessen matriisi ![H_f(1,1,-1/2)=\left [ \begin{smallmatrix} 2 & 2 & 0 \\ 2 & -1 & 2 \\ 0 & 2 & 2 \end{smallmatrix} \right ] H_f(1,1,-1/2)=\left [ \begin{smallmatrix} 2 & 2 & 0 \\ 2 & -1 & 2 \\ 0 & 2 & 2 \end{smallmatrix} \right ]](https://mycourses.aalto.fi/filter/tex/pix.php/67e1c90e30413fa189c4208b87d24fc9.gif) ja lasketaan matriisin ominaisarvot vaikkapa MATLABilla
ja lasketaan matriisin ominaisarvot vaikkapa MATLABilla
>> a = [2 2 0 ; 2 -1 2 ; 0 2 2]
a =
2 2 0
2 -1 2
0 2 2
>> eig(a)
ans =
-2.7016
2.0000
3.7016
Koska ominaisarvoissa on erimerkkisiä lukuja, niin funktiolla  on satulapiste pisteessä
on satulapiste pisteessä  .
.
4.2. Maksimi ja minimi
Puuttuu vielä.4.3. Lagrangen kertoimet
Lagrangen kertoimet
Usein optimointitehtävissä halutaan asettaa rajoitusehtoja
optimoitaville muuttujille.
Tyypillinen esimerkki tällaisesta tehtävästä on peltipurkin muodon optimointi: Halutaan minimoida purkin pinta-ala (eli käytetty materiaali)  niin, että tilavuus
niin, että tilavuus
 on vakio.
on vakio.
Duaalitehtävä: Halutaan maksimoida purkin tilavuus  siten, että pinta-ala
siten, että pinta-ala  on vakio.
Primaali- ja duaalitehtävillä on sama ratkaisu. Tämän sanoo maalaisjärkikin, mutta itse asiassa ratkaisuun johtavat yhtälötkin ovat (olennaisesti) samoja.
on vakio.
Primaali- ja duaalitehtävillä on sama ratkaisu. Tämän sanoo maalaisjärkikin, mutta itse asiassa ratkaisuun johtavat yhtälötkin ovat (olennaisesti) samoja.
Havaitaan, että mikäli ongelmalla on ratkaisu, niin ratkaisupisteessä  vektorien
vektorien  ja
ja  on oltava joko yhdensuuntaisia tai vastakkaissuuntaisia (mikäli
on oltava joko yhdensuuntaisia tai vastakkaissuuntaisia (mikäli  ).
Miksi? Koska muussa tapauksessa funktiolla
).
Miksi? Koska muussa tapauksessa funktiolla  olisi nollasta poikkeva suunnattu derivaatta käyrän
olisi nollasta poikkeva suunnattu derivaatta käyrän  tangentin suuntaan pisteessä
tangentin suuntaan pisteessä  , ja siis minimi ei voi olla pisteessä
, ja siis minimi ei voi olla pisteessä  .
.
Entä jos tehtävänä olisi maksimoida  ehdolla
ehdolla  ?
Entä jos tehtävänä olisi maksimoida
?
Entä jos tehtävänä olisi maksimoida  ehdolla
ehdolla  ?
?
Mikäli optimipiste on olemassa, se on Lagrangen funktion
 kriittinen piste (eli gradientin nollakohta).
Menetelmä yleistyy myös useammalle muuttujalle. Esimerkiksi kolmen muuttujan tapauksessa Lagrangen funktio on
kriittinen piste (eli gradientin nollakohta).
Menetelmä yleistyy myös useammalle muuttujalle. Esimerkiksi kolmen muuttujan tapauksessa Lagrangen funktio on
 missä
missä  on minimoitava funktio ja rajoite-ehdot ovat
on minimoitava funktio ja rajoite-ehdot ovat  sekä
sekä  .
.
Esimerkki
Minimoidaan funktio  ehdolla
ehdolla  .
Muodostetaan aluksi Lagrangen funktio
.
Muodostetaan aluksi Lagrangen funktio
 Yhtälöt kriittisille pisteille ovat
\begin{align*}
0 &=\frac{\partial L}{\partial x} = 2x(1+\lambda y),\\
0 &=\frac{\partial L}{\partial y} = 2y+\lambda x^2,\\
0 &=\frac{\partial L}{\partial \lambda}= x^2y-16,\\
\end{align*}
joista viimeinen on aina itse rajoitusehto.
Yhtälöt kriittisille pisteille ovat
\begin{align*}
0 &=\frac{\partial L}{\partial x} = 2x(1+\lambda y),\\
0 &=\frac{\partial L}{\partial y} = 2y+\lambda x^2,\\
0 &=\frac{\partial L}{\partial \lambda}= x^2y-16,\\
\end{align*}
joista viimeinen on aina itse rajoitusehto.
Ensimmäisestä yhtälöstä saadaan  tai
tai  , mutta
, mutta  on ristiriidassa kolmannen yhtälön kanssa.
Siten toisesta yhtälöstä
on ristiriidassa kolmannen yhtälön kanssa.
Siten toisesta yhtälöstä
 Tästä saadaan edelleen
Tästä saadaan edelleen  , ja
, ja  eli
eli  .
Ääriarvoja (mahdollisia minimejä) on siis kaksi
.
Ääriarvoja (mahdollisia minimejä) on siis kaksi  .
Pitää selvittää muilla keinoin, ovatko nämä minimejä vai maksimeja.
.
Pitää selvittää muilla keinoin, ovatko nämä minimejä vai maksimeja.
Esimerkki
Yritetään etsiä Lagrangen kertoimien menetelmällä funktion  minimi ehdolla
minimi ehdolla  .
Helposti havaitaan, että minimi
.
Helposti havaitaan, että minimi  saavutetaan pisteessä
saavutetaan pisteessä  .
.
Muodostetaan Lagrangen funktio
 Saadaan yhtälöt
Saadaan yhtälöt
 Nämä yhtälöt ovat keskenään ristiriidassa, joten ratkaisua niille ei ole. Huomaa, että
Nämä yhtälöt ovat keskenään ristiriidassa, joten ratkaisua niille ei ole. Huomaa, että  minimipisteessä. Tästä nähdään, että
Lagrangen kertoimet näkevät ääriarvoja vain
pisteissä, joissa
minimipisteessä. Tästä nähdään, että
Lagrangen kertoimet näkevät ääriarvoja vain
pisteissä, joissa  .
.
Esimerkki
Etsitään ääriarvot funktiolle  ehdoilla
ehdoilla  ja
ja  .
.
Koska  on jatkuva ja annettujen leikkausjoukkojen leikkaus on ympyräviiva (eli rajoitettu ja suljettu joukko), niin ääriarvot ovat olemassa.
Muodostetaan Lagrangen funktio
on jatkuva ja annettujen leikkausjoukkojen leikkaus on ympyräviiva (eli rajoitettu ja suljettu joukko), niin ääriarvot ovat olemassa.
Muodostetaan Lagrangen funktio
 Lagrangen funktion osittaisderivaatoista saadaan yhtälöt
\begin{align*}
& y+\lambda+2\mu x=0, \\
& x+\lambda+2\mu y=0, \\
& 2+\lambda+2\mu z=0, \\
& x+y+z = 0,\text{ ja } \\
& x^2+y^2+z^2-24=0.
\end{align*}
Kahden ensimmäisen yhtälön erotus johtaa yhtälöön
Lagrangen funktion osittaisderivaatoista saadaan yhtälöt
\begin{align*}
& y+\lambda+2\mu x=0, \\
& x+\lambda+2\mu y=0, \\
& 2+\lambda+2\mu z=0, \\
& x+y+z = 0,\text{ ja } \\
& x^2+y^2+z^2-24=0.
\end{align*}
Kahden ensimmäisen yhtälön erotus johtaa yhtälöön  , joten joko
, joten joko  tai
tai  . Tutkitaan molemmat tapaukset.
. Tutkitaan molemmat tapaukset.
Tapaus I ( ): Toisen ja kolmannen yhtälön perusteella
): Toisen ja kolmannen yhtälön perusteella
 Neljännestä yhtälöstä saadaan
Neljännestä yhtälöstä saadaan  ja
ja  . Viimeisen yhtälön perusteella
. Viimeisen yhtälön perusteella
 .
Koska
.
Koska  , saadaan
, saadaan  ja
ja  .
Nyt
.
Nyt  , joten
, joten  .
Yhdessä yhtälön
.
Yhdessä yhtälön  kanssa tästä saadaan kaksi kriittistä pistettä
kanssa tästä saadaan kaksi kriittistä pistettä
 Kummassakin pisteessä
Kummassakin pisteessä  .
.
Tapaus II ( ): Neljännestä yhtälöstä nähdään, että
): Neljännestä yhtälöstä nähdään, että
 , ja viimeisen yhtälön perusteella
, ja viimeisen yhtälön perusteella  eli
eli  .
Näin ollen, kriittiset pisteet ovat
.
Näin ollen, kriittiset pisteet ovat
 Saadaan
Saadaan
 Siten funktion
Siten funktion  maksimi on
maksimi on  ja minimi
ja minimi  .
.
5. PNS-menetelmä
Regressio-ongelma
Regressioanalyysissa pyritään valitsemaan parametrin  arvo siten, että käyrä
arvo siten, että käyrä  kulkisi mahdollisimman läheltä jokaista havaintopistettä
kulkisi mahdollisimman läheltä jokaista havaintopistettä  Tällaista optimaalisesti valittua käyrää kutsutaan regressiomalliksi
Tällaista optimaalisesti valittua käyrää kutsutaan regressiomalliksi  , jossa funktion
, jossa funktion  muoto on valittu tilanteen ja harkinnan mukaan. Kunhan
muoto on valittu tilanteen ja harkinnan mukaan. Kunhan  on valittu, niin eräs ratkaisu käyränsovitusongelmaan on pienimmän neliösumman menetelmä.
on valittu, niin eräs ratkaisu käyränsovitusongelmaan on pienimmän neliösumman menetelmä.
Pienimmän neliösumman menetelmä
Pienimmän neliösumman menetelmässä pyritään minimoimaan regressiomallin virhetermien 
 neliösummaa eli funktiota
neliösummaa eli funktiota  muuttamalla parametrivektorin
muuttamalla parametrivektorin  arvoa. Optimaalinen
arvoa. Optimaalinen  :n arvo on parametrin
:n arvo on parametrin  pienimmän neliösumman estimaatti eli PNS-estimaatti.
pienimmän neliösumman estimaatti eli PNS-estimaatti.
Kysymys: Miksi ei minimoitaisi lauseketta  neliösumman sijasta?
neliösumman sijasta?
PNS-sovitus
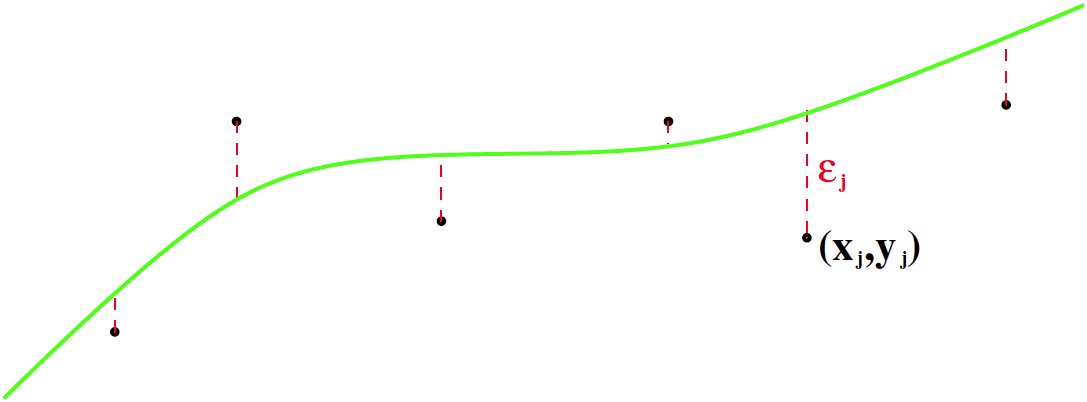
Kuvassa vihreällä parametreista  riippuva sovitettava funktio
riippuva sovitettava funktio  eräällä kiinteällä parametrin arvolla. Datapisteet
eräällä kiinteällä parametrin arvolla. Datapisteet  ja vastaavat virhetermit
ja vastaavat virhetermit  , kun
, kun  .
.
Lineaarinen regressio
Lineaarisessa regressiossa  jossa
jossa  ja neliösumma on
ja neliösumma on  Etsitään piste
Etsitään piste  siten, että
siten, että  .
.
Lasketaan osittaisderivaatta  Ratkaistaan nollakohta
Ratkaistaan nollakohta  missä
missä  on datavektorin
on datavektorin  komponenttien aritmeettinen keskiarvo.
komponenttien aritmeettinen keskiarvo.
Lasketaan seuraavaksi osittaisderivaatta  Sijoittamalla
Sijoittamalla  :n lauseke, saadaan
:n lauseke, saadaan  Ratkaistaan nollakohta:
Ratkaistaan nollakohta:  Tarkista jälkimmäinen yhtälö!
Tarkista jälkimmäinen yhtälö!
Esimerkki
Sovita PNS-suora dataan
 | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 |
|---|---|---|---|---|---|
 |
2.10 | 1.92 | 1.84 | 1.71 | 1.64 |
ja estimoi (ekstrapoloi)  kun
kun  .
.
Saadaan  ,
,  , ja
, ja  Siten
Siten  . Näin ollen
. Näin ollen  , ja kysytty estimaatti pisteessä
, ja kysytty estimaatti pisteessä  on
on  .
.
Esimerkki: Toisen asteen sovitus
Tutkitaan lisäaineen määrän  vaikutusta kuivumisaikaan
vaikutusta kuivumisaikaan  . Eri lisäaineen määrillä
. Eri lisäaineen määrillä  (grammaa) saatiin kuivumisajat
(grammaa) saatiin kuivumisajat  (tuntia),
(tuntia),  :
:
Huomataan, että kuivumisajan riippuvuus lisäaineen määrästä on epälineaarista.
Minimikohdan estimoimiseksi sovitetaan havaintoihin paraabeli 
Pienimmän neliösumman yhtälöryhmä mallille on  Näistä saadaan yhtälöryhmä
Näistä saadaan yhtälöryhmä  Laskemalla yhtälöryhmän kertoimet havainnoista saadaan
Laskemalla yhtälöryhmän kertoimet havainnoista saadaan 
Ratkaisuna ovat  ,
,  ja
ja  . Pienimmän neliösumman mielessä parhaiten havaintoihin liittyvä paraabeli on siten
. Pienimmän neliösumman mielessä parhaiten havaintoihin liittyvä paraabeli on siten 
6. Newtonin menetelmä
Newtonin iterointi
Newtonin menetelmällä voidaan löytää (vähintäänkin derivoituvan) funktion  nollakohta eli yhtälön
nollakohta eli yhtälön  ratkaisu.
Silloin kun menetelmä toimii, se suppenee hyvin nopeasti. Silloin kun ei, niin...
ratkaisu.
Silloin kun menetelmä toimii, se suppenee hyvin nopeasti. Silloin kun ei, niin...
Lähdetään liikkeelle jostakin pisteestä  , joka on alkuarvaus yhtälön ratkaisulle.
Arvioidaan funktiota
, joka on alkuarvaus yhtälön ratkaisulle.
Arvioidaan funktiota  sen tangenttisuoralla pisteessä, eli funktiolla
sen tangenttisuoralla pisteessä, eli funktiolla  .
Ratkaistaan yhtälö
.
Ratkaistaan yhtälö  . Toistetaan edellinen käyttäen alkuarvauksena lukua
. Toistetaan edellinen käyttäen alkuarvauksena lukua  luvun
luvun  sijasta jne.
Tämä menettely johtaa algoritmiin, jossa iteraatioaskeleet saadaan kaavasta
sijasta jne.
Tämä menettely johtaa algoritmiin, jossa iteraatioaskeleet saadaan kaavasta
 Suppeneminen ja löytyvä nollakohta riippuvat alkuarvauksesta
Suppeneminen ja löytyvä nollakohta riippuvat alkuarvauksesta  .
.
Esimerkki
Etsitään likiarvo luvulle  .
.
Koska  , niin valitaan
, niin valitaan  läheltä ratkaisua. Tässä
läheltä ratkaisua. Tässä  , joten
, joten  . Saadaan
. Saadaan


Huomaa, että  , eli jo kahdella iteraatiolla saatiin varsin hyvä likiarvo.
, eli jo kahdella iteraatiolla saatiin varsin hyvä likiarvo.
Esimerkki
Etsitään funktion  nollakohdat.
nollakohdat.
Piirtämällä kuvaaja nähdään, että funktiolla on vain yksi nollakohta jossain pisteiden  ja
ja  välissä. Asetetaan
välissä. Asetetaan  .
.
Koska  iteratioksi saadaan
iteratioksi saadaan
 Saadaan
Saadaan


Newtonin menetelmä monen muuttujan tapauksessa
Newtonin menetelmä toimii myös funktion  tapauksessa.
Tällöin iteraatiokaavassa oleva derivaatta pitää korvata Jacobin matriisilla
tapauksessa.
Tällöin iteraatiokaavassa oleva derivaatta pitää korvata Jacobin matriisilla
 Iteraatioaskeleeksi saadaan
Iteraatioaskeleeksi saadaan
 missä
missä  on
on  :n käänteismatriisi.
:n käänteismatriisi.
Esimerkki
Etsitään  , kun
, kun  ja
ja

Saadaan
 ja voidaan laskea
ja voidaan laskea
 mikä on terveellisintä tehdä tietokoneella.
mikä on terveellisintä tehdä tietokoneella.
Nähdään, että iteraatiot konvergoivat kohti pistettä  ,
joka on tehtävän tarkka (ja kaikesta päätellen ainoa) ratkaisu.
,
joka on tehtävän tarkka (ja kaikesta päätellen ainoa) ratkaisu.
7. Taso- ja avaruusintegraalit
7.1. Tasointegraali
Tasointegraali
Olkoon  joukko tasossa ja
joukko tasossa ja  skalaarikenttä. Halutaan määritellä tasointegraali
skalaarikenttä. Halutaan määritellä tasointegraali  Integraalin arvo on pinnan
Integraalin arvo on pinnan  ja
ja  -tason väliin jäävän alueen tilavuus.
-tason väliin jäävän alueen tilavuus.
Tutkitaan aluksi erikoistapausta ![D=[a,b]\times [c,d] D=[a,b]\times [c,d]](https://mycourses.aalto.fi/filter/tex/pix.php/9f6016ad24de0832985e8558f48470c2.gif) .
.
Yhden muuttujan tapaus
Yhden muuttujan tapauksessa integraali saadaan Riemannin summien raja-arvona.
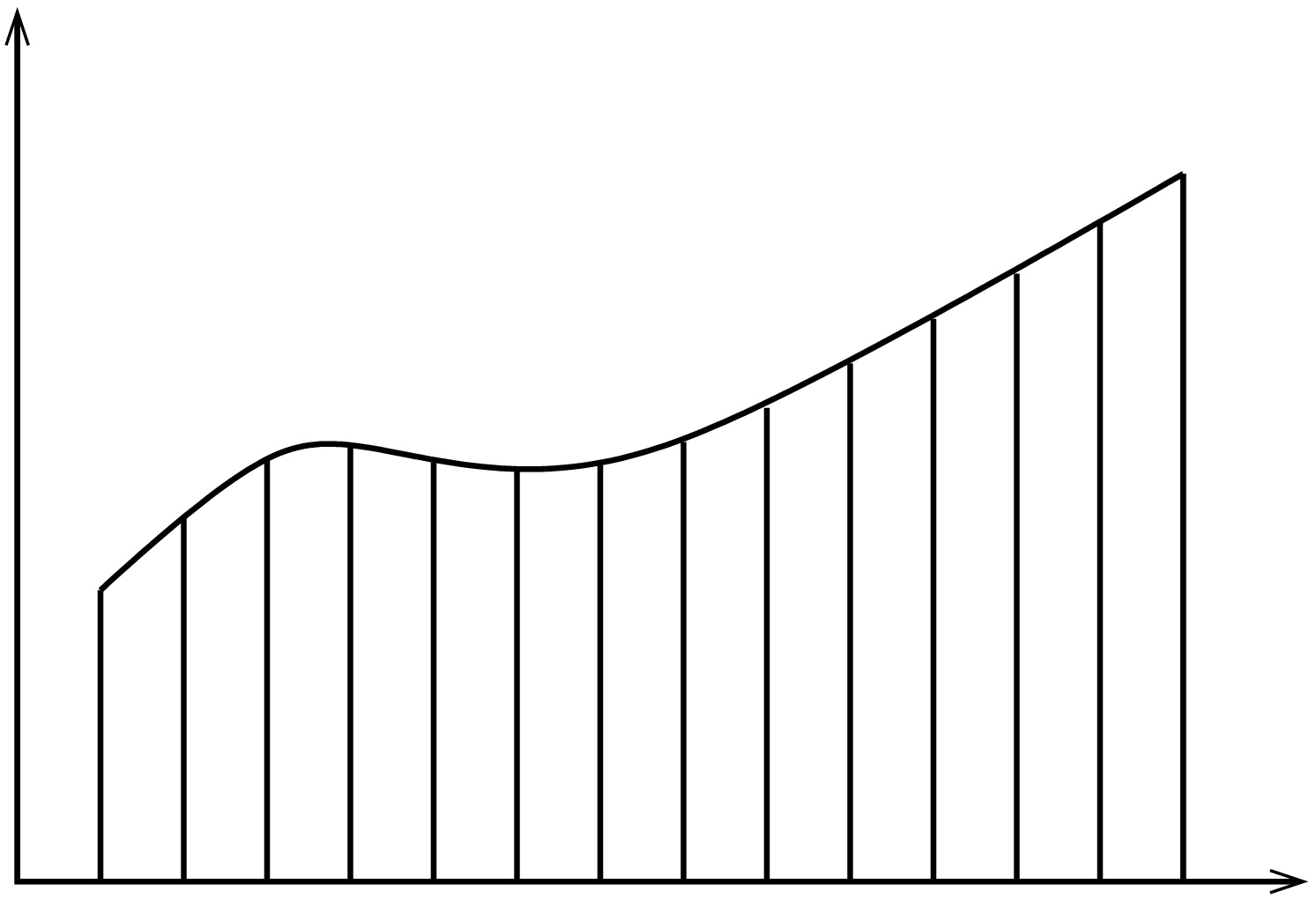
Formaalisti  missä
missä  on välin
on välin ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) tasavälinen jako ja
tasavälinen jako ja  on jakovälin pituus.
on jakovälin pituus.
Usean muuttujan tapaus (tasointegraali,  )
)
Jaetaan tason osajoukko ![D=[a,b]\times [c,d] D=[a,b]\times [c,d]](https://mycourses.aalto.fi/filter/tex/pix.php/9f6016ad24de0832985e8558f48470c2.gif) tasavälisesti ruudukoksi niin, että kummallakin akselilla on
tasavälisesti ruudukoksi niin, että kummallakin akselilla on  jakopistettä.
jakopistettä.
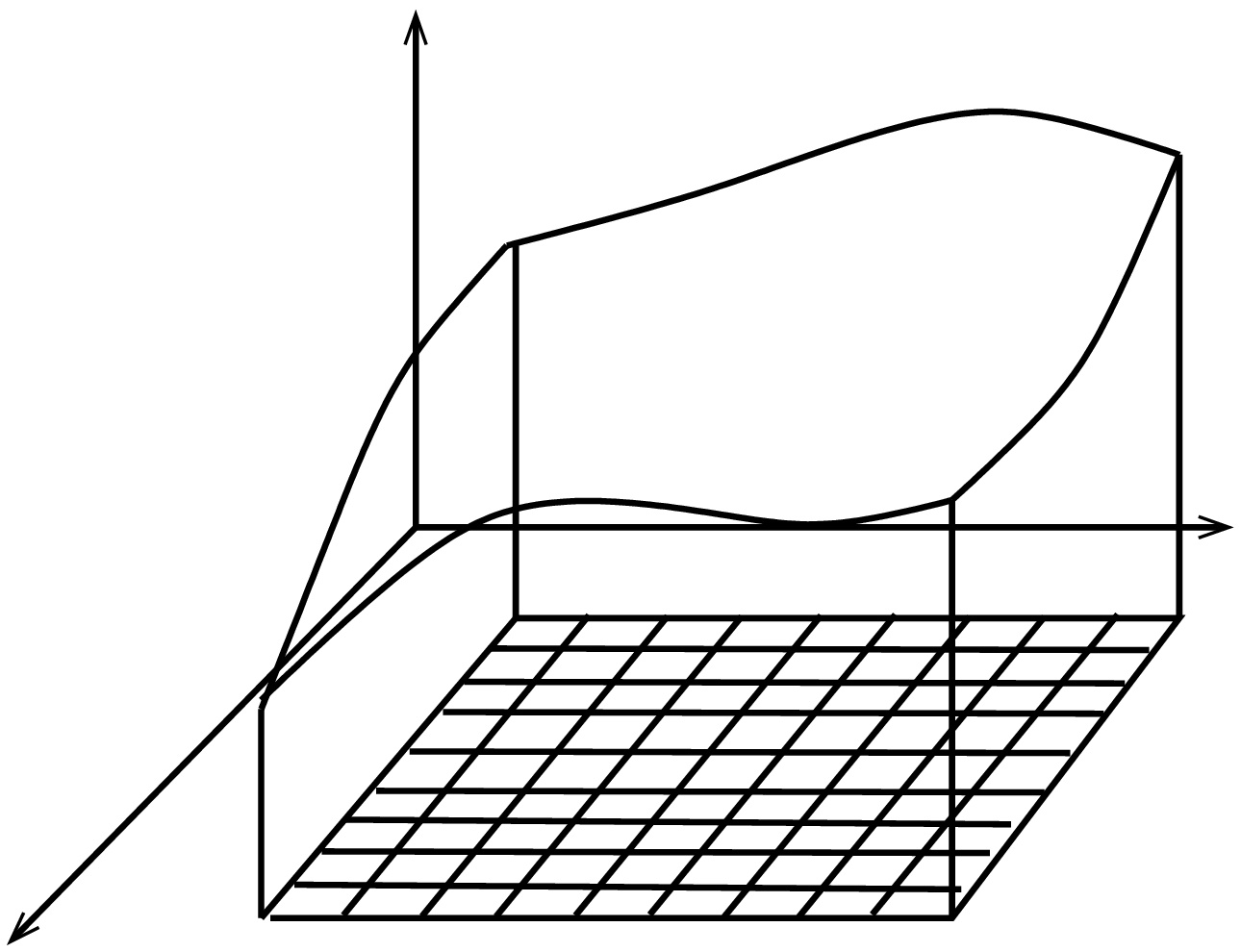
Nyt voidaan määritellä  missä
missä  ja
ja  sekä
sekä  vastaavat jakovälien pituutta
vastaavat jakovälien pituutta  ja
ja  -suunnassa:
-suunnassa: 
Huomautuksia
Yhden muuttujan tapauksessa integraaleille pätee Analyysin (ensimmäinen) peruslause: ![f(x)=\frac{d}{dx}\int_c^x f(t)\,dt,\textrm{ kun }c,x\in[a,b] f(x)=\frac{d}{dx}\int_c^x f(t)\,dt,\textrm{ kun }c,x\in[a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/142579790fdbdca671697cb8ba0740cc.gif) ja
ja ![f\colon [a,b]\to\mathbb{R} f\colon [a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/63f70baa16a71438df78c61a2f6709f2.gif) on jatkuva funktio.
on jatkuva funktio.
Analyysin peruslauseesta seuraa, että integrointi ja derivointi ovat toistensa vastaoperaatiota, mikä johtaa moniin integroinnissa hyödyllisiin kaavoihin. Analyysin peruslauseella ei kuitenkaan ole aivan samanlaista vastinetta usean muuttujan tapauksessa; Greenin, Gaussin ja Stokesin lauseet ovat kuitenkin sille sukua.
Moninkertainen integraali
Monen muuttujan integraaleja voidaan usein kuitenkin laskea moninkertaisina integraaleina. Kaksiulotteinen tapaus (integrointialue suorakulmio) ![\iint_D f(x,y)\,dA = \int_c^d \int_a^b f(x,y)\,dx\,dy, \text{ kun } D=[a,b]\times [c,d]. \iint_D f(x,y)\,dA = \int_c^d \int_a^b f(x,y)\,dx\,dy, \text{ kun } D=[a,b]\times [c,d].](https://mycourses.aalto.fi/filter/tex/pix.php/130a8aa2f794eb9ce5b967db988f8751.gif)
Mikäli funktio  on jatkuva, niin integroimisjärjestyksellä ei ole väliä integraalin arvon kannalta. Laskujen helppouden kannalta väliä kuitenkin on.
on jatkuva, niin integroimisjärjestyksellä ei ole väliä integraalin arvon kannalta. Laskujen helppouden kannalta väliä kuitenkin on.
Esimerkki
Olkoon  . Lasketaan
. Lasketaan 
Aluksi kirjoitetaan tasointegraali kaksinkertaisena integraalina, ja lasketaan \begin{align*} \iint_D xy^2\,dA &= \int_0^1\int_0^1 xy^2\,dx\,dy = \int_0^1\bigg[\frac{x^2y^2}{2}\bigg]_{x=0}^{1}\,dy \\ &= \int_0^1 \frac{y^2}{2}\,dy \bigg[\frac{y^3}{6}\bigg]_{y=0}^1 = \frac{1}{6}. \end{align*}
Integrointi yleisemmissä alueissa
Tutkitaan funktiota  , joka on määritelty tason osajoukossa
, joka on määritelty tason osajoukossa  . Tähän asti on oletettu, että
. Tähän asti on oletettu, että  on suorakulmio. Yleisemmässä tapauksessa voidaan tarkastella suorakulmiota
on suorakulmio. Yleisemmässä tapauksessa voidaan tarkastella suorakulmiota  , jolle
, jolle  . Jotta integraali olisi määritelty, täytyy joukon
. Jotta integraali olisi määritelty, täytyy joukon  olla ''siisti'' (riittää esimerkiksi, että reuna on paloittain sileä).
olla ''siisti'' (riittää esimerkiksi, että reuna on paloittain sileä).
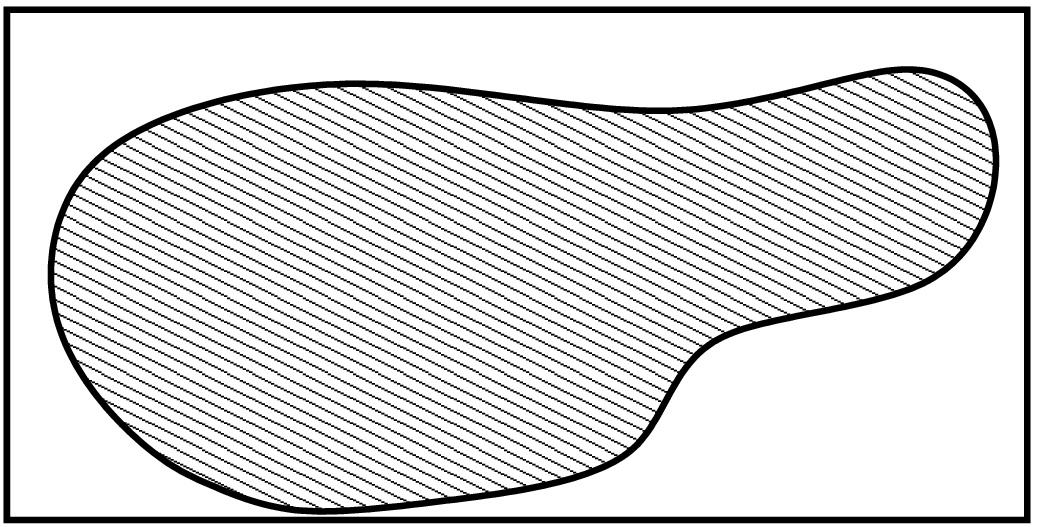
Määritellään funktio  seuraavasti:
seuraavasti:  Nyt voidaan määritellä
Nyt voidaan määritellä  Samaan tapaan voidaan määritellä myös avaruusintegraali ei-suorakulmaisen integroimisalueen tapauksessa:
Samaan tapaan voidaan määritellä myös avaruusintegraali ei-suorakulmaisen integroimisalueen tapauksessa:  kun
kun  on suorakulmainen särmiö ja
on suorakulmainen särmiö ja  .
.
Esimerkki
Olkoon  . Lasketaan funktion
. Lasketaan funktion  integraali yli alueen
integraali yli alueen  .
.
\begin{align*} &\iint_D xy\,dA = \int_0^1\bigg(\int_0^x xy\,dy\bigg)dx \\ &\quad \int_0^1\frac{xy^2}{2}\bigg|_{y=0}^x\,dx = \int_0^1\frac{x^3}{2}\,dx = \frac{x^4}{8}\bigg|_{x=0}^1 =\frac{1}{8}. \end{align*} Integrointi on mahdollista suorittaa myös toisessa järjestyksessä: \begin{align*} &\iint_D xy\,dA = \int_0^1\bigg(\int_y^1 xy\,dx\bigg)dy \\ &\quad = \int_0^1\frac{x^2y}{2}\bigg|_{x=y}^1\,dy = \int_0^1\frac{y}{2}-\frac{y^3}{2}\,dy \\ &\quad = \bigg[\frac{y^2}{4}-\frac{y^4}{8}\bigg]_{y=0}^1 = \frac{1}{4}-\frac{1}{8} = \frac{1}{8}. \\ \end{align*}
Esimerkki
7.2. Avaruusintegraali
Usean muuttujan tapaus (avaruusintegraali,  )
)
Tasointegraalia mukaillen voidaan samaan tapaan määritellä avaruusintegraali:  kun
kun ![D=[a_1,b_1]\times [a_2,b_2]\times[a_3,b_3] \subset \mathbb{R}^2 D=[a_1,b_1]\times [a_2,b_2]\times[a_3,b_3] \subset \mathbb{R}^2](https://mycourses.aalto.fi/filter/tex/pix.php/1b7f8ae96ce60ae2c94364916e82ebee.gif) ja
ja  . Tässä
. Tässä  Vieläkin useamman muuttujan funktioita
Vieläkin useamman muuttujan funktioita  , missä
, missä  , voi integroida samaan tapaan.
, voi integroida samaan tapaan.
Huomautuksia
Yhden muuttujan tapauksessa integraaleille pätee Analyysin (ensimmäinen) peruslause: ![f(x)=\frac{d}{dx}\int_c^x f(t)\,dt,\textrm{ kun }c,x\in[a,b] f(x)=\frac{d}{dx}\int_c^x f(t)\,dt,\textrm{ kun }c,x\in[a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/142579790fdbdca671697cb8ba0740cc.gif) ja
ja ![f\colon [a,b]\to\mathbb{R} f\colon [a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/63f70baa16a71438df78c61a2f6709f2.gif) on jatkuva funktio.
on jatkuva funktio.
Analyysin peruslauseesta seuraa, että integrointi ja derivointi ovat toistensa vastaoperaatiota, mikä johtaa moniin integroinnissa hyödyllisiin kaavoihin. Analyysin peruslauseella ei kuitenkaan ole aivan samanlaista vastinetta usean muuttujan tapauksessa; Greenin, Gaussin ja Stokesin lauseet ovat kuitenkin sille sukua.
Moninkertainen integraali
Monen muuttujan integraaleja voidaan usein kuitenkin laskea moninkertaisina integraaleina. Kolmiulotteinen tapaus (integrointialue suorakulmainen särmiö)  kun
kun ![D=[a_1,b_1]\times [a_2,b_2]\times [a_3,b_3] D=[a_1,b_1]\times [a_2,b_2]\times [a_3,b_3]](https://mycourses.aalto.fi/filter/tex/pix.php/698a7e1b8e7c18d974f5d5e90aa37ae3.gif) .
.
Mikäli funktio  on jatkuva, niin integroimisjärjestyksellä ei ole väliä integraalin arvon kannalta. Laskujen helppouden kannalta väliä kuitenkin on.
on jatkuva, niin integroimisjärjestyksellä ei ole väliä integraalin arvon kannalta. Laskujen helppouden kannalta väliä kuitenkin on.
Esimerkki
Olkoon . Lasketaan
. Lasketaan ![\iiint_D f(x,y,z)\,dV,\text{ missä } D=[0,2]\times [0,1] \times [-1,1]. \iiint_D f(x,y,z)\,dV,\text{ missä } D=[0,2]\times [0,1] \times [-1,1].](https://mycourses.aalto.fi/filter/tex/pix.php/7f3a53ca5d83258514f7ab3bc5319ec8.gif)
Kirjoitetaan avaruusintegraali kolminkertaisena integraalina. Lasketaan \begin{align*} &\iiint_D xye^z\,dV = \int_{-1}^1\int_0^1\int_0^2 xye^z\,dx\,dy\,dz \\ &\quad = \int_{-1}^1\int_0^1 \frac{x^2ye^z}{2}\bigg|_{x=0}^2\,dy\,dz = \int_{-1}^1\int_0^1 2ye^z\,dy\,dz \\ &\quad = \int_{-1}^1 y^2e^z\bigg|_{y=0}^1\,dz = \int_{-1}^1 e^z\,dz = e^z\Big|_{z=-1}^1 = e -e^{-1}. \end{align*}
Integrointi yleisemmissä alueissa
Tutkitaan funktiota  , joka on määritelty avaruuden osajoukossa
, joka on määritelty avaruuden osajoukossa  . Tähän asti on oletettu, että
. Tähän asti on oletettu, että  on suorakulmainen särmiö. Yleisemmässä tapauksessa voidaan tarkastella suorakulmaista särmiötä
on suorakulmainen särmiö. Yleisemmässä tapauksessa voidaan tarkastella suorakulmaista särmiötä  , jolle
, jolle  . Jotta integraali olisi määritelty, täytyy joukon
. Jotta integraali olisi määritelty, täytyy joukon  olla ''siisti'' (riittää esimerkiksi, että reuna on paloittain sileä).
olla ''siisti'' (riittää esimerkiksi, että reuna on paloittain sileä).
Määritellään funktio  seuraavasti:
seuraavasti:  Nyt voidaan määritellä avaruusintegraali ei-suorakulmaisen integroimisalueen tapauksessa:
Nyt voidaan määritellä avaruusintegraali ei-suorakulmaisen integroimisalueen tapauksessa:  kun
kun  on suorakulmainen särmiö ja
on suorakulmainen särmiö ja  .
.
7.3. Taso- ja avaruusintegraalien sovelluksia
Moninkertaisten integraalien sovelluksia
Tähän mennessä moninkertaisten integraalien sovelluksina on esiintynyt:
Mekaniikassa tulevat lisäksi vastaan nämä:
Kappaleen massa
 ja hitausmomentti kappaleen pyöriessä
ja hitausmomentti kappaleen pyöriessä  -akselin ympäri:
-akselin ympäri:
 Tässä
Tässä  on materiaalin tiheys pisteessä
on materiaalin tiheys pisteessä  .
.Kaksiulotteisen tasolevyn keskiön (painopiste)
 laskeminen
laskeminen
 jossa pinta-ala
jossa pinta-ala  on laskettu tasointegraalilla jo aiemmin.
on laskettu tasointegraalilla jo aiemmin.Jos levyn massa ei ole tasaisesti jakautunut, integraalia korjataan paikasta riippuvalla tiheydellä

 jossa massa
jossa massa  lasketaan tasointegraalilla.
lasketaan tasointegraalilla.
Massakeskipiste
Kolmiulotteisen kappaleen  massakeskipiste
massakeskipiste 


 missä
missä  on kappaleen tiheys pisteessä
on kappaleen tiheys pisteessä  ja
ja  on kappaleen massa (tilavuusintegraalilla).
Kaava voidaan kirjoittaa myös vektorimuodossa
on kappaleen massa (tilavuusintegraalilla).
Kaava voidaan kirjoittaa myös vektorimuodossa
 missä
missä  .
.
Esimerkki
Lasketaan epäyhtälöiden  ,
,  ja
ja  määräämän yksikkökuution
määräämän yksikkökuution  massakeskipiste, kun tiheys
massakeskipiste, kun tiheys  .
.
Huomautus. Yksikkökuutio  voidaan myös määritellä käyttäen niin kutsuttua karteesista tuloa:
voidaan myös määritellä käyttäen niin kutsuttua karteesista tuloa:
![D = [0,1] \times [0,1] \times [0,1] = [0,1]^3.
D = [0,1] \times [0,1] \times [0,1] = [0,1]^3.](https://mycourses.aalto.fi/filter/tex/pix.php/b48ea9f898096948af587144d5873259.gif) Tämä merkintätapa tarkoittaa samaa kuin ylläoleva määritelmä epäyhtälöiden avulla.
Tämä merkintätapa tarkoittaa samaa kuin ylläoleva määritelmä epäyhtälöiden avulla.
Vastaavasti
 Edelleen voidaan laskea
Edelleen voidaan laskea

 Massakeskipisteeksi saadaan
Massakeskipisteeksi saadaan

Hitausmomentti
Tarkastellaan tilannetta, jossa pistemäiset kappaleet kiertävät origoa  -tasossa ympyrän muotoista rataa pitkin
samalla kulmanopeudella.
-tasossa ympyrän muotoista rataa pitkin
samalla kulmanopeudella.
Kappaleiden yhteenlaskettu liike-energia saadaan laskemalla summa
![E= \sum_{i=1}^N \frac{1}{2} m_iv_i^2= \frac{1}{2} \Big[\sum_{i=1}^N m_i r_i^2\Big]\omega^2= \frac{1}{2}\Big[\sum_{i=1}^N m_i(x_i^2+y_i^2)\Big]\omega^2,
E= \sum_{i=1}^N \frac{1}{2} m_iv_i^2= \frac{1}{2} \Big[\sum_{i=1}^N m_i r_i^2\Big]\omega^2= \frac{1}{2}\Big[\sum_{i=1}^N m_i(x_i^2+y_i^2)\Big]\omega^2,](https://mycourses.aalto.fi/filter/tex/pix.php/a0a2db51ec02c4ba815fca426f88d181.gif) missä
missä  on kulmanopeus ja
on kulmanopeus ja  ,
,  sekä
sekä  ovat
ovat  :nnen kappaleen massa ja paikka.
Summaa
:nnen kappaleen massa ja paikka.
Summaa
 kutsutaan hitausmomentiksi.
Ajattelemalla
kutsutaan hitausmomentiksi.
Ajattelemalla  -akselin ympäri pyörivä kappale joukoksi "infinitesimaalisen pieniä" pisteitä, voidaan edelläolevasta summasta päätellä kappaleen liike-energia:
-akselin ympäri pyörivä kappale joukoksi "infinitesimaalisen pieniä" pisteitä, voidaan edelläolevasta summasta päätellä kappaleen liike-energia:
![E=\frac{1}{2} \bigg[ \iiint_D (x^2+y^2)\rho(x,y,z)\,dV\bigg]\omega^2
=\frac{1}{2} I_z\omega^2,
E=\frac{1}{2} \bigg[ \iiint_D (x^2+y^2)\rho(x,y,z)\,dV\bigg]\omega^2
=\frac{1}{2} I_z\omega^2,](https://mycourses.aalto.fi/filter/tex/pix.php/9d88f174f894c7b3fbbdb03af14d8cf2.gif) missä
missä
 on kappaleen hitausmomentti
on kappaleen hitausmomentti  -akselin suhteen (
-akselin suhteen ( ja massa-alkio
ja massa-alkio
 ).
).
Esimerkki
Lasketaan sylinterin
 hitausmomentti
hitausmomentti  -akselin suhteen, kun tiheys on vakio
-akselin suhteen, kun tiheys on vakio  .
.
Lasketaan


 Toisaalta sylinterin massa on
Toisaalta sylinterin massa on
 Siten hitausmomentti voidaan kirjoittaa
Siten hitausmomentti voidaan kirjoittaa

7.4. Yleinen muuttujanvaihto
Muuttujanvaihto tasointegraaleissa
Tutkitaan funktiota  , missä
, missä  ja
ja  ovat
ovat  :n osajoukkoja. Oletetaan, että funktion
:n osajoukkoja. Oletetaan, että funktion  kaikki osittaisderivaatat ovat olemassa ja jatkuvia. Lisäksi oletetaan, että
kaikki osittaisderivaatat ovat olemassa ja jatkuvia. Lisäksi oletetaan, että  on bijektio: Jokaista pistettä
on bijektio: Jokaista pistettä  vastaa yksikäsitteinen piste
vastaa yksikäsitteinen piste  , jolle
, jolle  . Tällöin erityisesti
. Tällöin erityisesti  .
.
Tutkitaan aluksi muuttujanvaihtoa tasointegraalin tapauksessa:  Tarvitaan tieto siitä, miten pinta-ala skaalautuu funktiossa
Tarvitaan tieto siitä, miten pinta-ala skaalautuu funktiossa  .
.
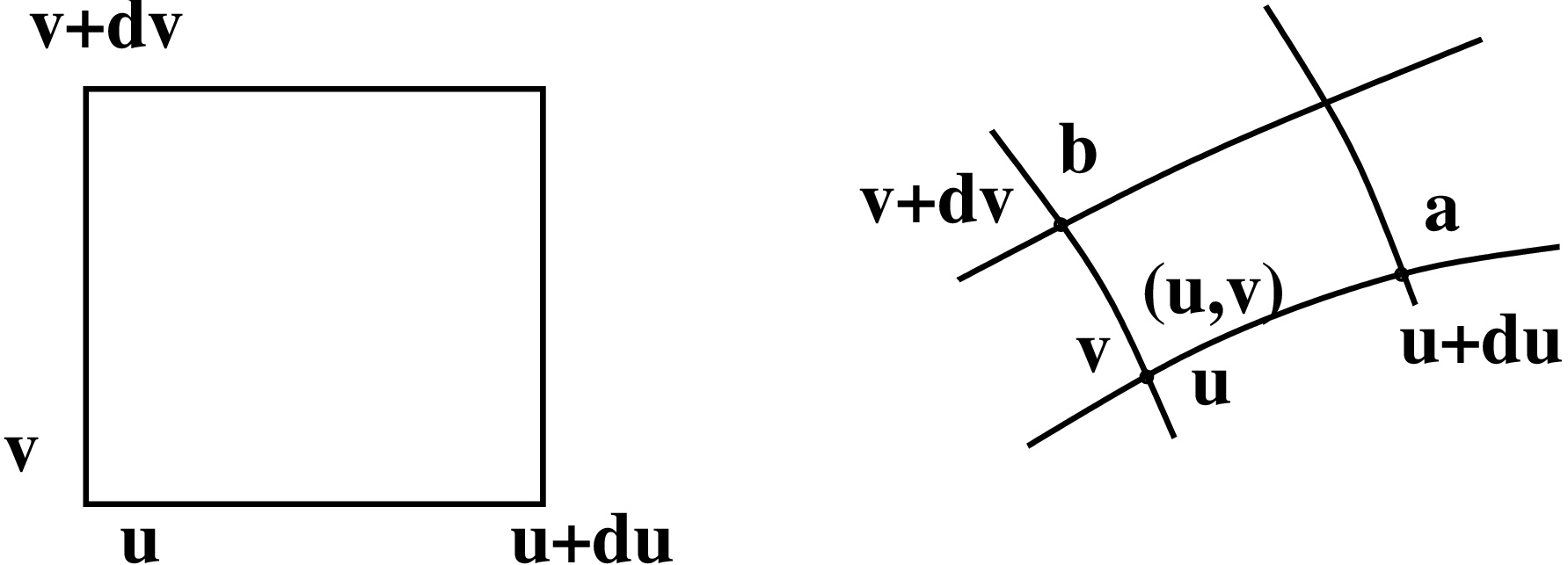
Ketjusäännöllä  Edettäessä vektorin
Edettäessä vektorin  suuntaan
suuntaan  -koordinaateissa, koordinaatti
-koordinaateissa, koordinaatti  on vakio ja siten
on vakio ja siten  . Saadaan
. Saadaan  Samaan tapaan voidaan päätellä, että
Samaan tapaan voidaan päätellä, että  Tässä
Tässä  ja
ja  ovat koordinaattiakseleiden suuntaiset yksikkövektorit.
ovat koordinaattiakseleiden suuntaiset yksikkövektorit.
Approksimaatiokaava pinta-alaelementin  muutokselle siis on
muutokselle siis on  Käytetään merkintää (huom. neliömatriiseille
Käytetään merkintää (huom. neliömatriiseille  )
)  Determinantti
Determinantti  on funktion
on funktion  Jacobin determinantti. Sille käytetään myös merkintää
Jacobin determinantti. Sille käytetään myös merkintää 
Jacobin determinantin itseisarvo  kertoo paikallisen pinta-alan muutoksen kuvattaessa
kertoo paikallisen pinta-alan muutoksen kuvattaessa  -koordinaattien infinitesimaalinen pinta-ala
-koordinaattien infinitesimaalinen pinta-ala  vastaavalle
vastaavalle  -koordinaateissa lausutulle pinta-alalle
-koordinaateissa lausutulle pinta-alalle  funktion
funktion  välityksellä.
välityksellä.
Tasointegraalin muuttujanvaihtokaavaksi siis saadaan  missä
missä  ja
ja  . Tässä
. Tässä  on integroimisalueiden
on integroimisalueiden  ja
ja  välinen bijektio. Jacobin determinantin etumerkki kertoo, onko
välinen bijektio. Jacobin determinantin etumerkki kertoo, onko  suunnan säilyttävä vai kääntävä. Itseisarvo tarvitaan, jotta positiivisen funktion integraali ei muuttuisi negatiiviseksi eräillä
suunnan säilyttävä vai kääntävä. Itseisarvo tarvitaan, jotta positiivisen funktion integraali ei muuttuisi negatiiviseksi eräillä  .
.
Esimerkki
Lasketaan neljän paraabelin  ,
,  ,
,  ja
ja  rajoittamaan alueen
rajoittamaan alueen  pinta-ala.
pinta-ala.
Huomataan, että integroimisalue kuvautuu suorakulmioksi ![G = [1/2 , 1] \times [1/3 , 1] G = [1/2 , 1] \times [1/3 , 1]](https://mycourses.aalto.fi/filter/tex/pix.php/f1c9f915649ee6dd8d38f38afa355761.gif) muunnoksella
muunnoksella 
Halutaan kuitenkin käänteiskuvaus  , joka vie koordinaatit
, joka vie koordinaatit  käyräviivaisille
käyräviivaisille  -koordinaateille. Lineaarialgebran perusteella
-koordinaateille. Lineaarialgebran perusteella  Lasketaan
Lasketaan  Saadaan myös
Saadaan myös 
Lasketaan edelleen 
 Tulokseksi siis saadaan
Tulokseksi siis saadaan  Yleensä ei käy niin onnellisesti, että sama koordinaatistomuunnos vie integroitavan alueen suorakulmiolle samalla kun integroitava funktio menee vakioksi.
Yleensä ei käy niin onnellisesti, että sama koordinaatistomuunnos vie integroitavan alueen suorakulmiolle samalla kun integroitava funktio menee vakioksi.
7.5. Muuttujanvaihto tasointegraalissa
Napakoordinaatit
Piste  voidaan kirjoittaa muodossa
voidaan kirjoittaa muodossa  , missä
, missä  ja
ja  . Napakulma
. Napakulma  on yksikäsitteinen jos
on yksikäsitteinen jos  .
.
Alkeisgeometriasta saadaan kaavat  Vrt. kompleksiluvun polaarimuoto
Vrt. kompleksiluvun polaarimuoto  .
.
Koordinaatistomuunnoksen  Jacobin determinantille saadaan kaava
Jacobin determinantille saadaan kaava  Siten muuttujanvaihtokaavaa varten saadaan pinta-alan venytys
Siten muuttujanvaihtokaavaa varten saadaan pinta-alan venytys  Tasointegraali napakoordinaateissa
Tasointegraali napakoordinaateissa  missä
missä  .
.
Esimerkki
(i) Olkoon  . Lasketaan napakoordinaateissa integraali
. Lasketaan napakoordinaateissa integraali  Saadaan
Saadaan 
(ii) Integraali  on erittäin tärkeä mm. todennäköisyyslaskennassa ja tilastotieteessä. Tämä integraali on vaikea, koska integraalifunktiota ei ole mahdollista kirjoittaa alkeisfunktioiden avulla.
on erittäin tärkeä mm. todennäköisyyslaskennassa ja tilastotieteessä. Tämä integraali on vaikea, koska integraalifunktiota ei ole mahdollista kirjoittaa alkeisfunktioiden avulla.
Integraali on kuitenkin mahdollista laskea seuraavan tempun avulla: Huomataan aluksi, että  Laskemalla epäoleellinen tasointegraali napakoordinaateissa
Laskemalla epäoleellinen tasointegraali napakoordinaateissa 

Nyt  , joten integraaliksi saadaan:
, joten integraaliksi saadaan:  Viemällä
Viemällä  tulee
tulee  ja siitä alkuperäisen integraalin arvo
ja siitä alkuperäisen integraalin arvo  Miksi temppu toimi?
Miksi temppu toimi?
7.6. Muuttujanvaihto avaruusintegraalissa
Muuttujanvaihto avaruusintegraalissa
Muunnoskaavat  ovat
ovat  Tällöin
Tällöin  missä
missä  Jos siis
Jos siis  , niin
, niin 
Sylinterikoordinaatit
Koordinaatit , missä
, missä  ,
,  ,
,  . Suoralla
. Suoralla  (eli
(eli  -akselilla) napakulma
-akselilla) napakulma  ei ole yksikäsitteinen.
ei ole yksikäsitteinen.
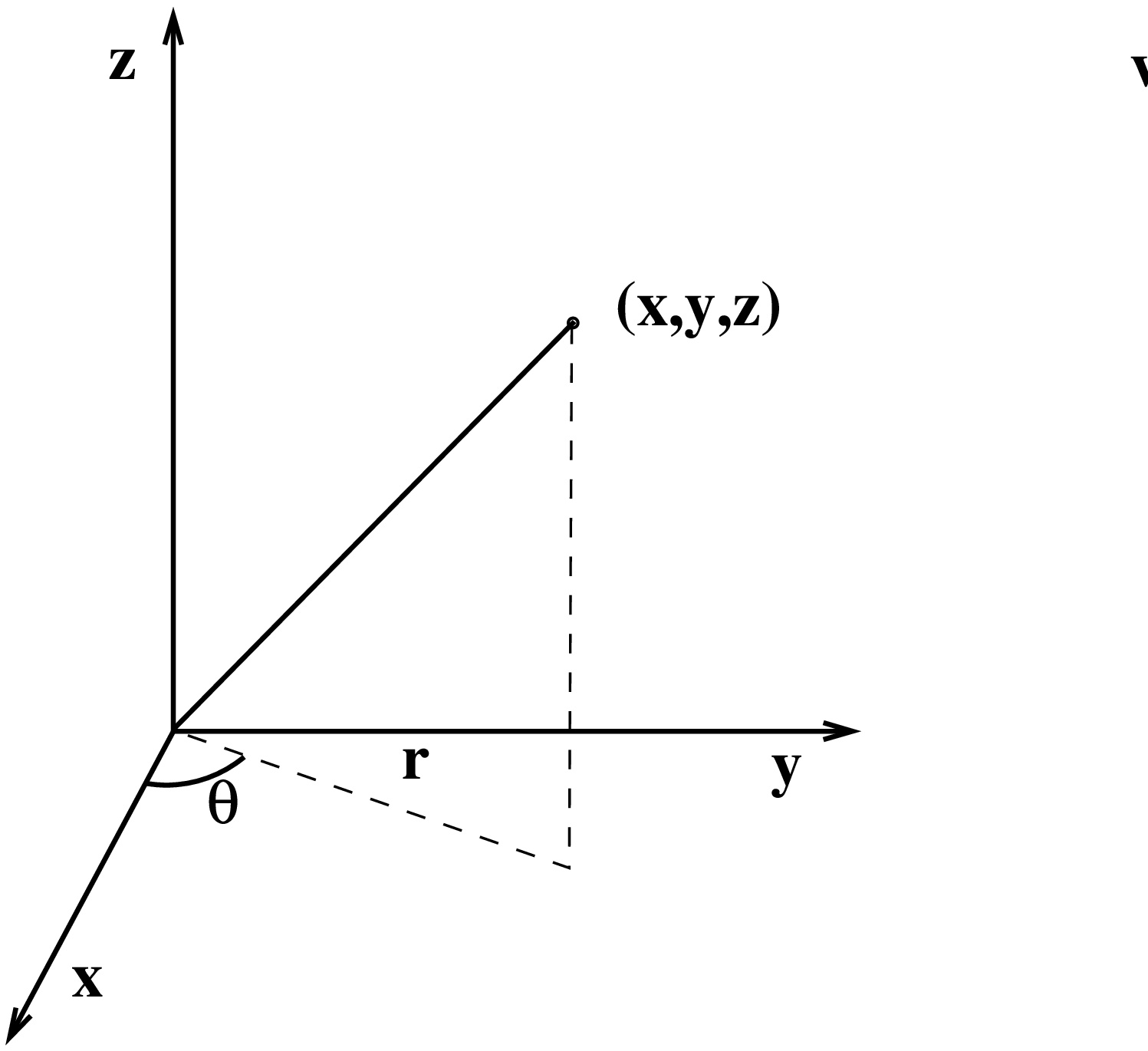
Tällöin muunnoskaavat  ovat \begin{align*} \begin{cases} x &= r\cos\theta, \\ y &= r\sin\theta, \\ z &= z. \end{cases} \end{align*} Ja muunnoksen Jacobin determinantiksi saadaan
ovat \begin{align*} \begin{cases} x &= r\cos\theta, \\ y &= r\sin\theta, \\ z &= z. \end{cases} \end{align*} Ja muunnoksen Jacobin determinantiksi saadaan 
Sylinterikoordinaateissa on helppo esittää pyörähdyskappaleita  -akselin ympäri muodossa
-akselin ympäri muodossa ![r = f(z), \quad \text{jossa} \quad z \in [a,b] \text{ ja } \theta \in [0, 2 \pi), r = f(z), \quad \text{jossa} \quad z \in [a,b] \text{ ja } \theta \in [0, 2 \pi),](https://mycourses.aalto.fi/filter/tex/pix.php/3ed9515366f90ebd6ca5ee292a63a54d.gif) missä
missä  on ei-negatiivinen funktio. Sylinterisymmetriset tehtävät!
on ei-negatiivinen funktio. Sylinterisymmetriset tehtävät!
Esimerkki
Lasketaan funktion  määräämän pyörähdyskappaleen
määräämän pyörähdyskappaleen  tilavuus
tilavuus 
 mikä lienee tuttu kaava.
mikä lienee tuttu kaava.
Pallokoordinaatit
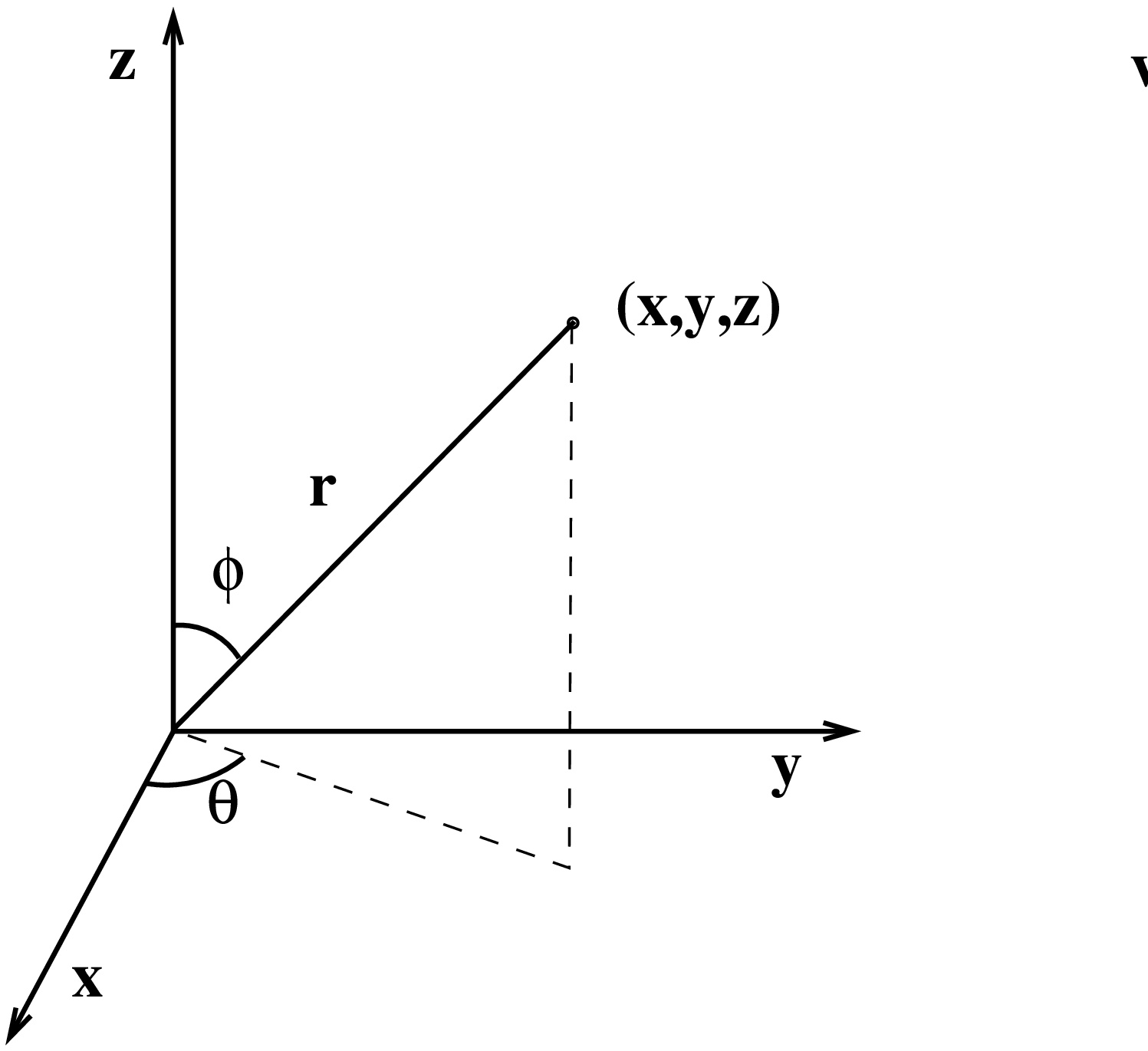
Korotus- eli napakulmaa  käytetään usein
käytetään usein  :n sijasta. Atsimuuttikulma
:n sijasta. Atsimuuttikulma  ja korotuskulma ovat yksikäsitteisiä, jos pisteen etäisyys
ja korotuskulma ovat yksikäsitteisiä, jos pisteen etäisyys  -akselista
-akselista  . Muunnoskaavat ovat \begin{align*} \begin{cases} x&=r\sin\phi \cos\theta,\\ y&=r\sin\phi \sin\theta,\\ z&=r\cos\phi, \end{cases} \end{align*} ja muunnoksen Jacobin determinantiksi saadaan
. Muunnoskaavat ovat \begin{align*} \begin{cases} x&=r\sin\phi \cos\theta,\\ y&=r\sin\phi \sin\theta,\\ z&=r\cos\phi, \end{cases} \end{align*} ja muunnoksen Jacobin determinantiksi saadaan 
Esimerkki
7.7. Epäoleelliset integraalit. Muuttujanvaihto taso- ja avaruusintegraaleissa
Epäoleelliset integraalit
Tähän asti integrointi on tapahtunut rajoitetussa alueessa rajoitetulle funktiolle (integrandille). Joskus voidaan kuitenkin integroida rajoittamattomia funktioita ja/tai rajoittamattomassa alueessa.
Tarkastellaan ainoastaan tapausta, jossa funktio  on ei-negatiivinen eli
on ei-negatiivinen eli  kaikilla
kaikilla  . Lasketaan funktion
. Lasketaan funktion  integraali alueessa suorien
integraali alueessa suorien  rajoittamassa rajoittamattomassa alueessa
rajoittamassa rajoittamattomassa alueessa  , jossa
, jossa  . Mikäli integraali on suppenee, sen arvo saadaan laskemalla
. Mikäli integraali on suppenee, sen arvo saadaan laskemalla 
 Integraalin laskemiseksi huomataan, että
Integraalin laskemiseksi huomataan, että  . Siten
. Siten 
Esimerkki
Olkoon  ja rajoittamaton funktio
ja rajoittamaton funktio  .
.
(ii) Lasketaan saman funktion integraali alueessa 

 Suppeneminen riippuu integroitavan funktion lisäksi myös alueesta!
Suppeneminen riippuu integroitavan funktion lisäksi myös alueesta!
7.8. Pintaintegraali
Kaksiulotteinen pinta-ala avaruudessa
Tutkitaan kaksiulotteista kaareutuvaa pintaa  , joka on (piirtämisen helpottamiseksi)
, joka on (piirtämisen helpottamiseksi)  -tason yläpuolella avaruudessa
-tason yläpuolella avaruudessa  .
.
Tarkastellaan aluksi  -tason neliön yläpuolelle jäävän osan pinta-alaa. Se on ilmeisesti suurempi tai yhtäsuuri kuin vastaavan neliön pinta-ala.
-tason neliön yläpuolelle jäävän osan pinta-alaa. Se on ilmeisesti suurempi tai yhtäsuuri kuin vastaavan neliön pinta-ala.
Tästä johtuen pinta-aladifferentiaali  on suurempi tai yhtäsuuri kuin kuin
on suurempi tai yhtäsuuri kuin kuin  . Itseasiassa
. Itseasiassa  saadaan, jos
saadaan, jos  projisoidaan
projisoidaan  -tasoon. Projektio voidaan kirjoittaa kaavana
-tasoon. Projektio voidaan kirjoittaa kaavana  missä
missä  on pinnan
on pinnan  normaalivektorin
normaalivektorin  ja
ja  -akselin suuntaisen yksikkövektorin
-akselin suuntaisen yksikkövektorin  välinen kulma. Toisaalta pistetulon määritelmästä saadaan
välinen kulma. Toisaalta pistetulon määritelmästä saadaan  ja siis
ja siis 
Aikaisemmin on johdettu pinnan (ylöspäin suunnatulle) normaalivektorille esitys  Saadaan
Saadaan  Lisäksi
Lisäksi  ja
ja  , joten
, joten  Kaltevuuden huomioiva korjaustekijä yleistää tasointegraalin pintaintegraaliksi.
Kaltevuuden huomioiva korjaustekijä yleistää tasointegraalin pintaintegraaliksi.
Esimerkki
Tarkastellaan sylinterin  ,
,  leikkaamaa palasta hyperbolisesta paraboloidista
leikkaamaa palasta hyperbolisesta paraboloidista  . Mikä on palasen pinta-ala?
. Mikä on palasen pinta-ala?
Lasketaan  Siten pinta-aladifferentiaaliksi saadaan
Siten pinta-aladifferentiaaliksi saadaan 

 napakoordinaateissa ilmaistuna.
napakoordinaateissa ilmaistuna.




































![\textbf{r}_1,\textbf{r}_2\colon [a,b]\to D\cup \{\textbf{y}_0\} \textbf{r}_1,\textbf{r}_2\colon [a,b]\to D\cup \{\textbf{y}_0\}](https://mycourses.aalto.fi/filter/tex/pix.php/99975a7d724c4ae4a075f28f977b7fc8.gif)























































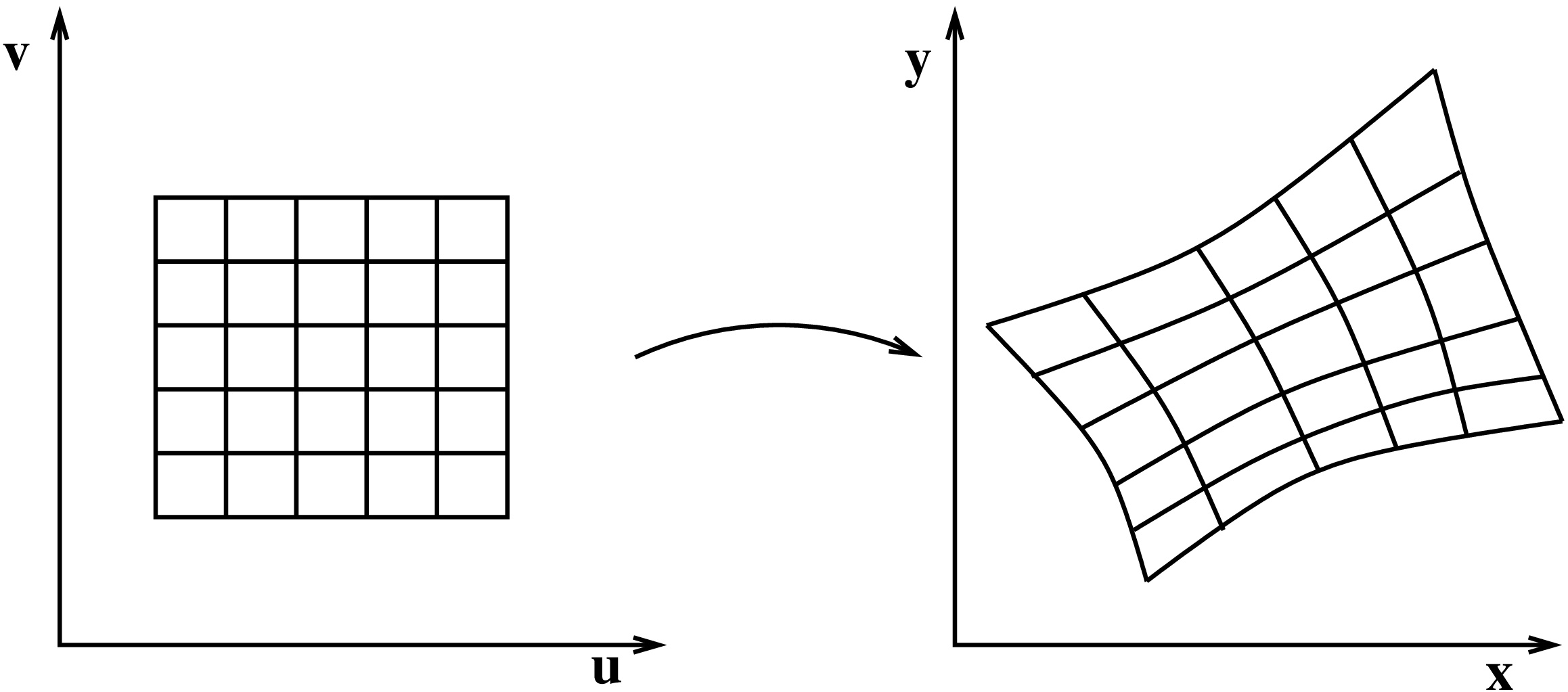












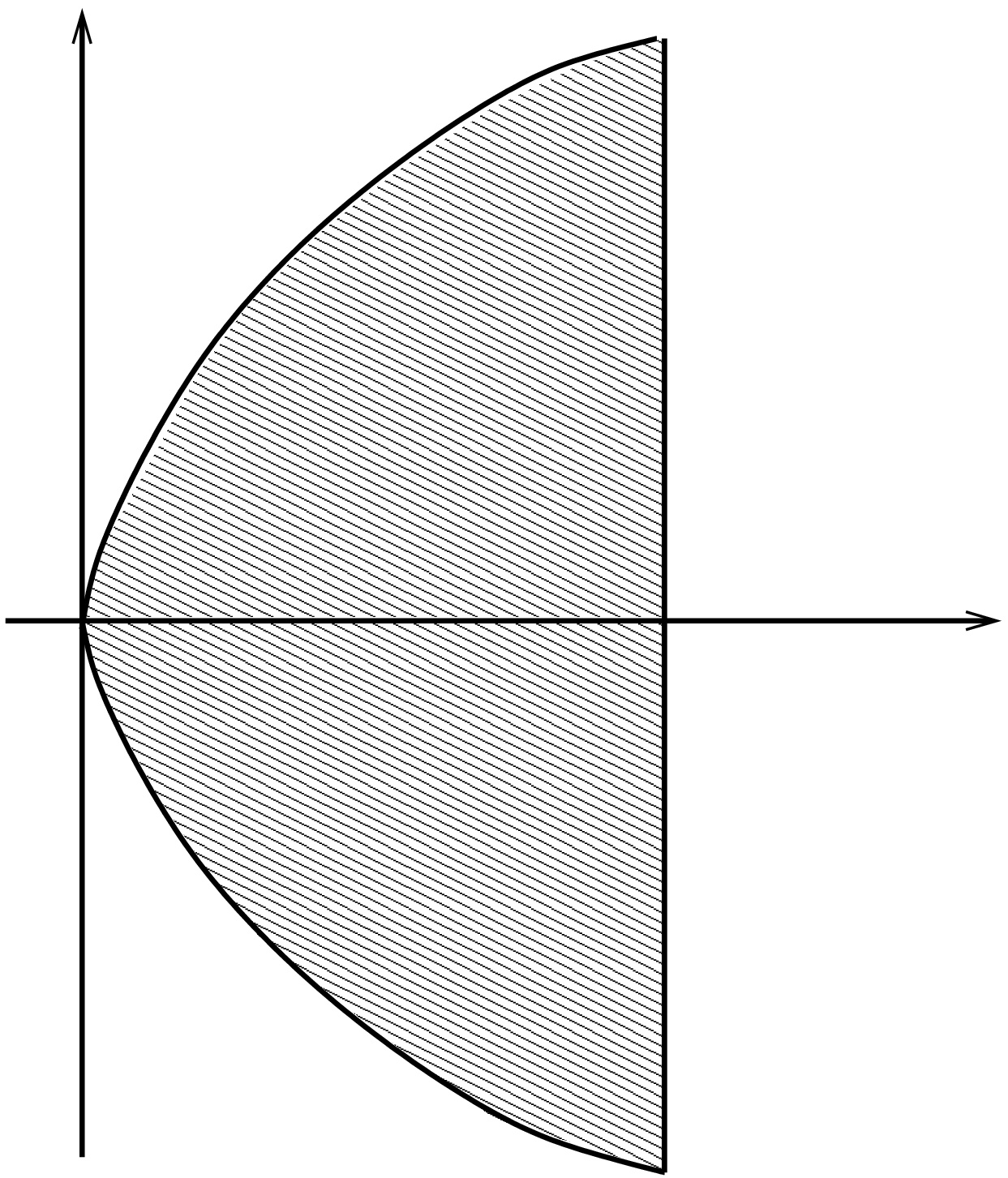



![= \frac{\pi}{4} \bigg|_{r=0}^a\frac{2}{3}(1+4r^2)^{3/2} =\frac{\pi}{6} \big[(1+4a^2)^{3/2} -1\big]. = \frac{\pi}{4} \bigg|_{r=0}^a\frac{2}{3}(1+4r^2)^{3/2} =\frac{\pi}{6} \big[(1+4a^2)^{3/2} -1\big].](https://mycourses.aalto.fi/filter/tex/pix.php/71e226128ed6cf6aadc1612006256a4c.gif)