Differential and Integral Calculus
| Site: | MyCourses |
| Course: | MS-A0111 - Differential and Integral Calculus 1, Lecture, 13.9.2021-27.10.2021 |
| Book: | Differential and Integral Calculus |
| Printed by: | Guest user |
| Date: | Wednesday, 19 February 2025, 1:10 AM |
1. Sequences
Basics of sequences
This section contains the most important definitions about sequences. Through these definitions the general notion of sequences will be explained, but then restricted to real number sequences.
Note. Characteristics of the set  give certain characteristics to the sequence. Because
give certain characteristics to the sequence. Because  is ordered, the terms of the sequence are ordered.
is ordered, the terms of the sequence are ordered.
Definition: Terms and Indices
A sequence can be denoted denoted as
instead of  The numbers
The numbers  are called the terms of the sequence.
are called the terms of the sequence.
Because of the mapping
 we can assign a unique number
we can assign a unique number  to each term. We write this number as a subscript and define it as the index; it follows that we can identify any term of the sequence by its index.
to each term. We write this number as a subscript and define it as the index; it follows that we can identify any term of the sequence by its index.
A few easy examples
Example 1: The sequence of natural numbers
The sequence  defined by
defined by  is called the sequence of natural numbers. Its first few terms are:
is called the sequence of natural numbers. Its first few terms are:
 This special sequence has the property that every term is the same as its index.
This special sequence has the property that every term is the same as its index.
![]()
Example 2: The sequence of triangular numbers
Triangular numbers get their name due to the following geometric visualization: Stacking coins to form a triangular shape gives the following diagram:
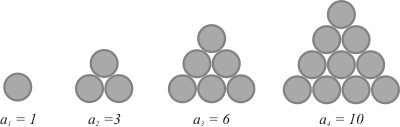
To the first coin in the first layer we add two coins in a second layer to form the second picture  . In turn, adding three coins to
. In turn, adding three coins to  forms
forms  . From a mathematical point of view, this sequence is the result of summing natural numbers. To calculate the 10th triangular number we need to add the first 10 natural numbers:
. From a mathematical point of view, this sequence is the result of summing natural numbers. To calculate the 10th triangular number we need to add the first 10 natural numbers:
 In general form the sequence is defined as:
In general form the sequence is defined as: 
This motivates the following definition:
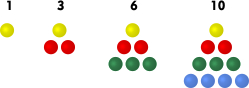
Example 3: Sequence of square numbers
The sequence of square numbers  is defined by:
is defined by:  . The terms of this sequence can also be illustrated by the addition of coins.
. The terms of this sequence can also be illustrated by the addition of coins.
Interestingly, the sum of two consecutive triangular numbers is a square number. So, for example, we have:  and
and  . In general this gives the relationship:
. In general this gives the relationship:

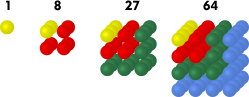
Example 4: Sequence of cube numbers
Analogously to the sequence of square number, we give the definition of cube numbers as  The first terms of the sequence are:
The first terms of the sequence are:  .
.
Example 5.
Example 6.
Given the sequence  with
with  , i.e.
, i.e.
 Let
Let  be its 1st difference sequence. Then it follows that
be its 1st difference sequence. Then it follows that
 A term of
A term of  has the general form
has the general form

Some important sequences
There are a number of sequences that can be regarded as the basis of many ideas in mathematics, but also can be used in other areas (e.g. physics, biology, or financial calculations) to model real situations. We will consider three of these sequences: the arithmetic sequence, the geometric sequence, and Fibonacci sequence, i.e. the sequence of Fibonacci numbers.
The arithmetic sequence
There are many definitions of the arithmetic sequence:
Definition A: Arithmetic sequence
A sequence  is called the arithmetic sequence, when the difference
is called the arithmetic sequence, when the difference  between two consecutive terms is constant, thus:
between two consecutive terms is constant, thus:

Note: The explicit rule of formation follows directly from definition A:
 For the
For the  th term of an arithmetic sequence we also have the recursive formation rule:
th term of an arithmetic sequence we also have the recursive formation rule:

Definition B: Arithmetic sequence
A non-constant sequence  is called an arithmetic sequence (1st order) when its 1st difference sequence is a sequence of constant value.
is called an arithmetic sequence (1st order) when its 1st difference sequence is a sequence of constant value.
This rule of formation gives the arithmetic sequence its name: The middle term of any three consecutive terms is the arithmetic mean of the other two, for example:
Example 1.
The sequence of natural numbers
 is an arithmetic sequence, because the difference,
is an arithmetic sequence, because the difference,  , between two consecutive terms is always given as
, between two consecutive terms is always given as  .
.
The geometric sequence
The geometric sequence has multiple definitions:
Definition: Geometric sequence
A sequence  is called a geometric sequence when the ratio of any two consecutive terms is always constant
is called a geometric sequence when the ratio of any two consecutive terms is always constant  , thus
, thus

Note.The recursive relationship
 of the terms of the geometric sequence and the explicit formula for the calculation of the n
th term of a geometric sequence
of the terms of the geometric sequence and the explicit formula for the calculation of the n
th term of a geometric sequence
 follows directly from the definition.
follows directly from the definition.
Again the name and the rule of formation of this sequence are connected: Here, the middle term of three consecutive terms is the geometric mean of the other two, e.g.:

Example 2.
Let  and
and  be fixed positive numbers. The sequence
be fixed positive numbers. The sequence  with
with  , i.e.
, i.e.
 is a geometric sequence. If
is a geometric sequence. If  the sequence is monotonically increasing. If
the sequence is monotonically increasing. If  it is strictly decreasing. The corresponding range
it is strictly decreasing. The corresponding range  is finite in the case
is finite in the case  (namely, a singleton), otherwise it is infinite.
(namely, a singleton), otherwise it is infinite.
The Fibonacci sequence
The Fibonacci sequence is famous because it plays a role in many biological processes, for instance in plant growth, and is frequently found in nature. The recursive definition is:
Definition: Fibonacci sequence
Let  and let
and let
 for
for  . The sequence
. The sequence  is then called the Fibonacci sequence. The terms of the sequence are called the Fibonacci numbers.
is then called the Fibonacci sequence. The terms of the sequence are called the Fibonacci numbers.
The sequence is named after the Italian mathematician Leonardo of Pisa (ca. 1200 AD), also known as Fibonacci (son of Bonacci). He considered the size of a rabbit population and discovered the number sequence:

Example 3.
The structure of sunflower heads can be described by a system of two spirals, which radiate out symmetrically but contra rotating from the centre; there are 55 spirals which run clockwise and 34 which run counter-clockwise.
Pineapples behave very similarly. There we have 21 spirals running in one direction and 34 running in the other. Cauliflower, cacti, and fir cones are also constructed in this manner.

Convergence, divergence and limits
The following chapter deals with the convergence of sequences. We will first introduce the idea of zero sequences. After that we will define the concept of general convergence.
Preliminary remark: Absolute value in 
The absolute value function  is fundamental in the study of convergence of real number sequences. Therefore we should summarise again some of the main characteristics of the absolute value function:
is fundamental in the study of convergence of real number sequences. Therefore we should summarise again some of the main characteristics of the absolute value function:
Graph of the absolute value function
Theorem: Calculation Rule for the Absolute Value
Parts 1.-3. Results follow directly from the definition and by dividing it up into separate cases of the different signs of  and
and 
Part 4. Here we divide the triangle inequality into different cases.
Case 1.
First let  . Then it follows that
. Then it follows that
 and the desired inequality is shown.
and the desired inequality is shown.
Finally we consider the case  and
and  . Here we have two subcases:
. Here we have two subcases:
For
 we have
we have  and thus
and thus  from the definition of absolute value. Because
from the definition of absolute value. Because  then
then  and therefore also
and therefore also  . Overall we have:
. Overall we have:

For
 then
then  . We have
. We have  . Because
. Because  , we have
, we have  and thus
and thus  . Overall we have:
. Overall we have:

The case  and
and  we prove it analogously to the case 3, in which
we prove it analogously to the case 3, in which  and
and  are exchanged.
are exchanged.
Zero sequences
Definition: Zero sequence
A sequence  s called a zero sequence, if for every
s called a zero sequence, if for every  there exists an index
there exists an index  such that
such that
 for every
for every  . In this case we also say that the sequence converges to zero.
. In this case we also say that the sequence converges to zero.
Informally: We have a zero sequence, if the terms of the sequence with high enough indices are arbitrarily close to zero.
Example 1.
The sequence  defined by
defined by  , i.e.
, i.e.  is called the harmonic sequence. Clearly, it is positive for all
is called the harmonic sequence. Clearly, it is positive for all  , however as
, however as  increases the absolute value of each term decreases getting closer and closer to zero.
increases the absolute value of each term decreases getting closer and closer to zero.
Take for example  , then choosing the index
, then choosing the index  , it follows that
, it follows that  , for all
, for all  .
.
The harmonic sequence converges to zero
Example 2.
Consider the sequence
 Let
Let  .We then obtain the index
.We then obtain the index  in this manner that for all terms
in this manner that for all terms  where
where 
 .
.
Note. To check whether a sequence is a zero sequence, you must choose an (arbitrary)  where
where  . Then search for a index
. Then search for a index  , after which all terms
, after which all terms  are smaller then said
are smaller then said  .
.
Example 3.
We consider the sequence  , defined by
, defined by

Because of the factors  two consecutive terms have different signs; we call a sequence whose signs change in this way an alternating sequence.
two consecutive terms have different signs; we call a sequence whose signs change in this way an alternating sequence.
We want to show that this sequence is a zero sequence. According to the definition we have to show that for every  there exist
there exist  , such that we have the inequality:
, such that we have the inequality:
 for every term
for every term  where
where  .
.
Theorem: Characteristics of Zero sequences
Parts 1 and 2. If  is a zero sequence, then according to the definition there is an index
is a zero sequence, then according to the definition there is an index  , such that
, such that  for every
for every  and an arbitrary
and an arbitrary  . But then we have
. But then we have  ; this proves parts 1 and 2 are correct.
; this proves parts 1 and 2 are correct.
Part 3. If  , then the result is trivial. Let
, then the result is trivial. Let  and choose
and choose  such that
such that
 for all
for all  .
Rearranging we get:
.
Rearranging we get:

Part 4.
Because  is a zero sequence, by the definition we have
is a zero sequence, by the definition we have  for all
for all  . Analogously, for the zero sequence
. Analogously, for the zero sequence  there is a
there is a  with
with  for all
for all  .
.
Then for all  it follows (using the triangle inequality) that:
it follows (using the triangle inequality) that:

Convergence, divergence
The concept of zero sequences can be expanded to give us the convergence of general sequences:
Example 4.
We consider the sequence  where
where
 By plugging in large values of
By plugging in large values of  , we can see that for
, we can see that for 
 and therefore we can postulate that the limit is
and therefore we can postulate that the limit is  .
.
For a vigorous proof, we show that for every  there exists an index
there exists an index  , such that for every term
, such that for every term  with
with  the following relationship holds:
the following relationship holds:

Firstly we estimate the inequality:

Now, let  be an arbitrary constant. We then choose the index
be an arbitrary constant. We then choose the index  , such that
, such that
 Finally from the above inequality we have:
Finally from the above inequality we have:
 Thus we have proven the claim and so by definition
Thus we have proven the claim and so by definition  is the limit of the sequence.
is the limit of the sequence.
If a sequence is convergent, then there is exactly one number which is the limit. This characteristic is called the uniqueness of convergence.
Assume  ; choose
; choose  with
with  Then in particular
Then in particular ![[a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset. [a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset.](https://mycourses.aalto.fi/filter/tex/pix.php/4bac60723e473d9697be98685ce7659a.gif)
Because  converges to
converges to  , there is, according to the definition of convergence, a index
, there is, according to the definition of convergence, a index  with
with  for
for  Furthermore, because
Furthermore, because  converges to
converges to  there is also a
there is also a  with
with  for
for  For
For  we have:
we have:
 Consequently we have obtained
Consequently we have obtained  , which is a contradiction as
, which is a contradiction as  . Therefore the assumption must be wrong, so
. Therefore the assumption must be wrong, so  .
.
Definition: Divergent, Limit
If provided that a sequence  and an
and an  exist, to which the sequence converges, then the sequence is called convergent and
exist, to which the sequence converges, then the sequence is called convergent and  is called the limit of the sequence, otherwise it is called divergent.
is called the limit of the sequence, otherwise it is called divergent.
Notation.  is convergent to
is convergent to  is also written:
is also written:
 Such notation is allowed, as the limit of a sequence is always unique by the above Theorem (provided it exists).
Such notation is allowed, as the limit of a sequence is always unique by the above Theorem (provided it exists).
Rules for convergent sequences
Theorem: Rules
Let  and
and  be sequences with
be sequences with  and
and  . Then for
. Then for  it follows that:
it follows that:
Informally: Sums, differences and products of convergent sequences are convergent.
Part 1. Let  . We must show, that for all
. We must show, that for all  it follows that:
it follows that:
 The left hand side we estimate using:
The left hand side we estimate using:

Because  and
and  converge, for each given
converge, for each given  it holds true that:
it holds true that:

Therefore
 for all numbers
for all numbers  . Therefore the sequence
. Therefore the sequence
 is a zero sequence and the desired inequality is shown.
is a zero sequence and the desired inequality is shown.
Part 2. Let  . We have to show, that for all
. We have to show, that for all 
 Furthermore an estimation of the left hand side follows:
Furthermore an estimation of the left hand side follows:
 We choose a number
We choose a number  , such that
, such that  for all
for all  and
and  . Such a value of
. Such a value of  exists by the Theorem of convergent sequences being bounded. We can then use the estimation:
exists by the Theorem of convergent sequences being bounded. We can then use the estimation:
 For all
For all  we have
we have  and
and  , and - putting everything together - the desired inequality it shown.
, and - putting everything together - the desired inequality it shown.
 '; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
/* fibonacci sequence */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox : [-1, 40, 10, -5 ],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
straightFirst : false, highlight : false,
drawZero : true,
ticks : { drawLabels : false, minorTicks : 0, majorHeight : 15, label : { highlight : false, offset : [0, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
straightFirst : false, highlight : false,
ticks : { minorTicks : 0, majorHeight : 15, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 5; };
var a_k = [1, 1];
var newbar = function(k) {
var y;
if(k-1 > a_k.length-1) {
y = a_k[k-3] + a_k[k-2];
a_k.push(y);
} else {
y = a_k[k-1];
}
return board.create('polygon', [[k-1/4, 0], [k+1/4, 0], [k+1/4, y], [k-1/4, y]] , {
vertices : { visible : false },
borders : { strokeColor : 'black', strokeOpacity : .6, highlight : false },
fillColor : '#b2caeb',
fixed : true,
highlight : false
});
}
var bars = [];
for(var i=0; i < 9; i++) {
const k = i+1;
board.create('text', [k-.1, -.6, function() { return '
'; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
/* fibonacci sequence */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox : [-1, 40, 10, -5 ],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
straightFirst : false, highlight : false,
drawZero : true,
ticks : { drawLabels : false, minorTicks : 0, majorHeight : 15, label : { highlight : false, offset : [0, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
straightFirst : false, highlight : false,
ticks : { minorTicks : 0, majorHeight : 15, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 5; };
var a_k = [1, 1];
var newbar = function(k) {
var y;
if(k-1 > a_k.length-1) {
y = a_k[k-3] + a_k[k-2];
a_k.push(y);
} else {
y = a_k[k-1];
}
return board.create('polygon', [[k-1/4, 0], [k+1/4, 0], [k+1/4, y], [k-1/4, y]] , {
vertices : { visible : false },
borders : { strokeColor : 'black', strokeOpacity : .6, highlight : false },
fillColor : '#b2caeb',
fixed : true,
highlight : false
});
}
var bars = [];
for(var i=0; i < 9; i++) {
const k = i+1;
board.create('text', [k-.1, -.6, function() { return ' '; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
'; }], {
useMathJax : true,
strokeColor : '#2183de',
fontSize : 13,
fixed : true,
highlight : false
});
board.fullUpdate();
})();
'; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
board.create('point', [i, 1/i], {
size : 4,
name : '',
strokeWidth : .5,
strokeColor : 'black',
face : 'diamond',
fillColor : '#cf4490',
fixed : true
});
}
board.fullUpdate();
})();
'; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
'; }], {
useMathJax : true,
strokeColor : '#2183de',
fontSize : 13,
fixed : true,
highlight : false
});
board.fullUpdate();
})();
'; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
board.create('point', [i, 1/i], {
size : 4,
name : '',
strokeWidth : .5,
strokeColor : 'black',
face : 'diamond',
fillColor : '#cf4490',
fixed : true
});
}
board.fullUpdate();
})();
2. Series
Table of Content
Convergence
Convergence
If the sequence of partial sums  has a limit
has a limit  , then
the series of the sequence
, then
the series of the sequence  converges
and its sum is
converges
and its sum is  . This is denoted by
. This is denoted by

Divergence of a series
A series that does ot converge is divergent. This can happen in three different ways:
- the partial sums tend to infinity
- the partial sums tend to minus infinity
- the sequence of partial sums oscillates so that there is no limit.
In the case of a divergent series the symbol  does not really mean anything (it isn't a number). We can then interpret it as the sequence of partial sums, which is always well-defined.
does not really mean anything (it isn't a number). We can then interpret it as the sequence of partial sums, which is always well-defined.
Basic results
Geometric series
A geometric series
 converges if
converges if  (or
(or  ), and then its sum is
), and then its sum is  . If
. If  , then
the series diverges.
, then
the series diverges.
Rules of summation
Properties of convergent series:
Note: Compared to limits, there is no similar product-rule for series, because
even for sums of two elements we have
 The correct generalization is the Cauchy product of two series, where also
the cross terms are taken into account.
The correct generalization is the Cauchy product of two series, where also
the cross terms are taken into account.
Note: The property  cannot be used to justify the convergence of a series; cf. the following examples.
This is one of the most common elementary mistakes many people do when
studying series!
cannot be used to justify the convergence of a series; cf. the following examples.
This is one of the most common elementary mistakes many people do when
studying series!
Example
Explore the convergence of the series

Solution. The limit of the general term of the series is
 As this is different from zero, the series diverges.
As this is different from zero, the series diverges.
This is a classical result first proven in the 14th century by Nicole Oresme after which a number of proofs using different approaches have been published. Here we present two different approaches for comparison.
i) An elementary proof by contradiction. Suppose, for the sake of contradiction, that the harmonic series converges i.e. there exists  such that
such that  . In this case
. In this case
 Now, by direct comparison we get
Now, by direct comparison we get
 hence following from the Properties of summation it follows that
hence following from the Properties of summation it follows that

 But this implies that
But this implies that  , a contradiction. Therefore, the initial assumption that the harmonic series converges must be false and thus the series diverges.
, a contradiction. Therefore, the initial assumption that the harmonic series converges must be false and thus the series diverges.
ii) Proof using integral: Below a histogram with heights  lies the graph of
the function
lies the graph of
the function  , so comparing areas we have
, so comparing areas we have
 as
as  .
.

Positive series
Summing a series is often difficult or even impossible in closed form, sometimes only a numerical approximation can be calculated. The first goal then is to find out whether a series is convergent or divergent.
A series  is positive,
if
is positive,
if  for all
for all  .
.
Convergence of positive series is quite straightforward:
Theorem 2.
A positive series converges if and only if the sequence of partial sums is bounded from above.
Why? Because the partial sums form an increasing sequence.
Example
Show that the partial sums of a superharmonic series
 satisfy
satisfy  for all
for all  , so the series converges.
, so the series converges.
Solution. This is based on the formula
 for
for  , as it implies that
, as it implies that
 for all
for all  .
.
This can also be proven with integrals.
Leonhard Euler found out in 1735 that the sum is actually  . His
proof was based on comparison of the series and product expansion of
the sine function.
. His
proof was based on comparison of the series and product expansion of
the sine function.
Absolute convergence
Theorem 3.
An absolutely convergent series converges (in the usual sense) and

This is a special case of the Comparison principle, see later.
Suppose that  converges. We study separately the positive and negative
parts of
converges. We study separately the positive and negative
parts of  :
Let
:
Let  Since
Since  , the positive series
, the positive series  and
and  converge by Theorem 2.
Also,
converge by Theorem 2.
Also,  , so
, so  converges as a difference of two convergent series.
converges as a difference of two convergent series.

Example
Study the convergence of the alternating (= the signs alternate) series

Solution. Since
 and the superharmonic series
and the superharmonic series
 converges, then the original series is absolutely convergent. Therefore
it also converges in the usual sense.
converges, then the original series is absolutely convergent. Therefore
it also converges in the usual sense.
Alternating harmonic series
The usual convergence and absolute convergence are, however, different concepts:
Example
The alternating harmonic series
 converges, but not absolutely.
converges, but not absolutely.
(Idea) Draw a graph of the partial sums  to get the idea that
even and odd index partial sums
to get the idea that
even and odd index partial sums  and
and  are monotone and
converge to the same limit.
are monotone and
converge to the same limit.
The sum of this series is  , which can be derived by integrating the
formula of a geometric series.
, which can be derived by integrating the
formula of a geometric series.
points are joined by line segments for visualization purposes
Convergence tests
Comparison test
The preceeding results generalize to the following:
Proof for Majorant. Since  and
and
 then
then  is convergent as a difference of two convergent positive series.
Here we use the elementary convergence property (Theorem 2.) for positive series;
this is not a circular reasoning!
is convergent as a difference of two convergent positive series.
Here we use the elementary convergence property (Theorem 2.) for positive series;
this is not a circular reasoning!
Proof for Minorant. It follows from the assumptions that the partial sums of  tend to infinity, and the series is divergent.
tend to infinity, and the series is divergent.

Example
Solution. Since
 for all
for all  , the first series is convergent by the majorant principle.
, the first series is convergent by the majorant principle.
On the other hand,  for all
for all  , so the second series has a divergent harmonic series as a minorant.
The latter series is thus divergent.
, so the second series has a divergent harmonic series as a minorant.
The latter series is thus divergent.
Ratio test
In practice, one of the best ways to study convergence/divergence of a series is the so-called ratio test, where the terms of the sequence are compared to a suitable geometric series:
Limit form of ratio test
(Idea) For a geometric series the ratio of two consecutive terms is
exactly  . According to the ratio test, the convergence of some other
series can also be investigated in a similar way, when the exact ratio
. According to the ratio test, the convergence of some other
series can also be investigated in a similar way, when the exact ratio
 is replaced by the above limit.
is replaced by the above limit.
In the formal definition of a limit  . Thus starting from some index
. Thus starting from some index
 we have
we have
 and the claim follows from Theorem 4.
and the claim follows from Theorem 4.
In the case  the general term of the series does not go to zero,
so the series diverges.
the general term of the series does not go to zero,
so the series diverges.
The last case  does not give any information.
does not give any information.
This case occurs for the harmonic series ( , divergent!) and superharmonic
(
, divergent!) and superharmonic
( , convergent!) series. In these cases the convergence or divergence
must be settled in some other way, as we did before.
, convergent!) series. In these cases the convergence or divergence
must be settled in some other way, as we did before.

3. Continuity
Table of Content
In this section we define a limit of a function  at a point
at a point  . It is assumed that the reader is already familiar with limit of a sequence, the real line and the general concept of a function of one real variable.
. It is assumed that the reader is already familiar with limit of a sequence, the real line and the general concept of a function of one real variable.
Limit of a function
For a subset of real numbers, denoted by  , assume that
, assume that  is such point that there is a sequence of points
is such point that there is a sequence of points  such that
such that  as
as  . Here the set
. Here the set  is often the set of all real numbers, but sometimes an interval (open or closed).
is often the set of all real numbers, but sometimes an interval (open or closed).
Example 1.
Note that it is not necessary for  to be in
to be in  . For example, the sequence
. For example, the sequence  as
as  in
in ![S=]0,2[ S=]0,2[](https://mycourses.aalto.fi/filter/tex/pix.php/29d87817bfac0840e7915f2622194590.gif) , and
, and  for all
for all  but
but  is not in
is not in  .
.
Limit of a function
Example 3.
Example 5.
One-sided limits
An important property of limits is that they are always unique. That is, if  and
and  , then
, then  . Although a function may have only one limit at a given point, it is sometimes useful to study the behavior of the function when
. Although a function may have only one limit at a given point, it is sometimes useful to study the behavior of the function when  approaches the point
approaches the point  from the left or the right side. These limits are called the left and the right limit of the function
from the left or the right side. These limits are called the left and the right limit of the function  at
at  , respectively.
, respectively.
Definition 2: One-sided limits
Suppose  is a set in
is a set in  and
and  is a function defined on the set
is a function defined on the set  . Then we say that
. Then we say that  has a left limit
has a left limit  at
at  , and write
, and write
 if,
if,  as
as  for every sequence
for every sequence  in the set
in the set
![S\cap ]-\infty,x_0[ =\{ x\in S : x < x_0 \} S\cap ]-\infty,x_0[ =\{ x\in S : x < x_0 \}](https://mycourses.aalto.fi/filter/tex/pix.php/c65f5d0e098970db4a09f85ad08fada6.gif) , such that
, such that  as
as  .
.
Similarly, we say that  has a right limit
has a right limit  at
at  , and write
, and write
 if,
if,  as
as  for every sequence
for every sequence  in the set
in the set
![S\cap ]x_0,\infty[ =\{ x\in S : x_0 < x \} S\cap ]x_0,\infty[ =\{ x\in S : x_0 < x \}](https://mycourses.aalto.fi/filter/tex/pix.php/34e4590988ffbbcc84fe6f2077270c14.gif) , such that
, such that  as
as  .
.
Example 6.
Limit rules
The following limit rules are immediately obtained from the definition and basic algebra of real numbers.
Limits and continuity
In this section, we define continuity of the function. The intutive idea behind continuity is that the graph of a continuous function is a connected curve. However, this is not sufficient as a mathematical definition for several reasons. For example, by using this definition, one cannot easily decide if  is a continuous function or not.
is a continuous function or not.
Example 1.
Example 2.
Let  . We define a function
. We define a function  by
by
 Then
Then
 Therefore
Therefore  is not continuous at the point
is not continuous at the point  .
.
Some basic properties of continuous functions of one real variable are given next. From the limit rules (Theorem 2) we obtain:
Theorem 3.
The sum, the product and the difference of continuous functions are continuous. Then, in particular, polynomials are continuous functions. If  and
and  are polynomials and
are polynomials and  , then
, then  is continuous at a point
is continuous at a point  .
.
A composition of continuous functions is continuous if it is defined:
Theorem 4.
Let  and
and  . Suppose that
. Suppose that  is continuous at a point
is continuous at a point  and
and  is continuous at
is continuous at  . Then
. Then  is continuous at a point
is continuous at a point  .
.
Note. If  is continuous, then
is continuous, then  is continuous.
is continuous.
Why?
Note. If  and
and  are continuous, then
are continuous, then  and
and  are continuous. (Here
are continuous. (Here  .)
.)
Why?
 '}], {
strokeColor : colors[1],
fontSize : 16,
visible : false
});
l[2] = board.create('text', [-4, 3, function() { return '
'}], {
strokeColor : colors[1],
fontSize : 16,
visible : false
});
l[2] = board.create('text', [-4, 3, function() { return ' '}], {
strokeColor : colors[2],
fontSize : 16,
visible : false
});
g[0] = board.create('functiongraph', [f0, -6, 6], {
visible : true,
strokeWidth : 1.5,
strokeColor : colors[0],
highlight : false
});
g[1] = board.create('functiongraph', [f1, -6, 6], {
visible : false,
strokeWidth : 1.5,
strokeColor : colors[1],
highlight : false
});
g[2] = board.create('functiongraph', [f2, -6, 6], {
visible : false,
strokeWidth : 1.5,
strokeColor : colors[2],
highlight : false
});
var currentGraph = g[0];
var currentLabel = l[0];
select.on('drag', function() {
currentGraph.setAttribute({ visible : false });
currentLabel.setAttribute({ visible : false });
currentGraph = g[select.Value()];
currentLabel = l[select.Value()];
currentGraph.setAttribute({ visible : true });
currentLabel.setAttribute({ visible : true, useMathJax : true });
select.setAttribute({ fillColor : colors[select.Value()] });
board.update();
});
board.fullUpdate();
})();
/* Example 2. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox16', {
boundingbox : [-3.5, 4.5, 3.5, -1.25],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]]);
xaxis.removeAllTicks();
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
drawZero : true,
ticks : { majorHeight : 5, minorTicks : 0, ticksDistance : 1.0 }
});
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var xtick = board.create('segment', [[1, .05],[1, -.1]], {
strokeWidth : 1, strokeColor : 'black', strokeOpacity : .4,
highlight : false });
var f = function(x) { return 2; }
var g = function(x) { return 3; }
board.create('functiongraph', [f, -3.5, 1], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [g, 1, 3.5], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.create('point', [1, f(1)], {
name : '',
fillColor : 'white',
strokeColor : 'black',
strokeWidth : .5,
size : 2,
fixed : true,
showInfobox : false
});
board.create('point', [1, g(1)], {
name : '',
fillColor : 'black',
strokeColor : 'black',
strokeWidth : .5,
size : 2,
fixed : true,
showInfobox : false
});
var x0 = board.create('text', [1, 0, function() { return '
'}], {
strokeColor : colors[2],
fontSize : 16,
visible : false
});
g[0] = board.create('functiongraph', [f0, -6, 6], {
visible : true,
strokeWidth : 1.5,
strokeColor : colors[0],
highlight : false
});
g[1] = board.create('functiongraph', [f1, -6, 6], {
visible : false,
strokeWidth : 1.5,
strokeColor : colors[1],
highlight : false
});
g[2] = board.create('functiongraph', [f2, -6, 6], {
visible : false,
strokeWidth : 1.5,
strokeColor : colors[2],
highlight : false
});
var currentGraph = g[0];
var currentLabel = l[0];
select.on('drag', function() {
currentGraph.setAttribute({ visible : false });
currentLabel.setAttribute({ visible : false });
currentGraph = g[select.Value()];
currentLabel = l[select.Value()];
currentGraph.setAttribute({ visible : true });
currentLabel.setAttribute({ visible : true, useMathJax : true });
select.setAttribute({ fillColor : colors[select.Value()] });
board.update();
});
board.fullUpdate();
})();
/* Example 2. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox16', {
boundingbox : [-3.5, 4.5, 3.5, -1.25],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]]);
xaxis.removeAllTicks();
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
drawZero : true,
ticks : { majorHeight : 5, minorTicks : 0, ticksDistance : 1.0 }
});
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var xtick = board.create('segment', [[1, .05],[1, -.1]], {
strokeWidth : 1, strokeColor : 'black', strokeOpacity : .4,
highlight : false });
var f = function(x) { return 2; }
var g = function(x) { return 3; }
board.create('functiongraph', [f, -3.5, 1], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [g, 1, 3.5], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.create('point', [1, f(1)], {
name : '',
fillColor : 'white',
strokeColor : 'black',
strokeWidth : .5,
size : 2,
fixed : true,
showInfobox : false
});
board.create('point', [1, g(1)], {
name : '',
fillColor : 'black',
strokeColor : 'black',
strokeWidth : .5,
size : 2,
fixed : true,
showInfobox : false
});
var x0 = board.create('text', [1, 0, function() { return ' '; }], {
useMathJax : true
});
board.fullUpdate();
})();
'; }], {
useMathJax : true
});
board.fullUpdate();
})();
Delta-epsilon definition
The so-called  -definition for continuity is given next. The basic idea behind this test is that, for a function
-definition for continuity is given next. The basic idea behind this test is that, for a function  continuous at
continuous at  , the values of
, the values of  should get closer to
should get closer to  as
as  gets closer to
gets closer to  .
.
This is the standard definition of continuity in mathematics, because it also works for more general classes of functions than ones on this course, but it not used in high-school mathematics. This important definition will be studied in-depth in Analysis 1 / Mathematics 1.
Example 3.
 ', fillColor : '#bd4444', snapWidth : 0.01,
label : { useMathJax : true, strokeColor : '#bd4444', offset : [0, 25] }});
var x1 = board.create('glider', [1/2, 0, xaxis],
{ name: '
', fillColor : '#bd4444', snapWidth : 0.01,
label : { useMathJax : true, strokeColor : '#bd4444', offset : [0, 25] }});
var x1 = board.create('glider', [1/2, 0, xaxis],
{ name: ' ', strokeColor : 'black', strokeWidth : .5, fillColor : '#446abd', showinfobox : false,
label : { useMathJax : true, strokeColor : '#446abd', offset : [5, 25] } });
/*board.suspendUpdate();*/
var y1 = board.create('point', [0, function(){return f(x1.X());}],
{ name : '
', strokeColor : 'black', strokeWidth : .5, fillColor : '#446abd', showinfobox : false,
label : { useMathJax : true, strokeColor : '#446abd', offset : [5, 25] } });
/*board.suspendUpdate();*/
var y1 = board.create('point', [0, function(){return f(x1.X());}],
{ name : ' ', size : 2, strokeColor : 'black', strokeWidth : .5, fillColor : '#bd4444',
showinfobox : false, highlight : false,
label : { useMathJax : true, strokeColor : '#bd4444', offset : [5, 25] }});
var y2 = board.create('point', [0, function(){return f(x1.X())-s.Value();}], { visible : false });
var y3 = board.create('point', [0, function(){return f(x1.X())+s.Value();}], { visible : false });
var z1 = board.create('point', [function(){return y1.Y()/4;}, function(){return y1.Y();}], { visible : false });
var z2 = board.create('point', [function(){return y2.Y()/4;}, function(){return y2.Y();}], { visible : false });
var z3 = board.create('point', [function(){return y3.Y()/4;}, function(){return y3.Y();}], { visible : false });
var v1 = board.create('segment', [z1, y1], { strokeColor : '#bd4444', strokeWidth : 1, highlight : false });
var v2 = board.create('line', [z2, y2], { strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var v3 = board.create('line', [z3, y3], { strokeColor: '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var epsilon = board.create('polygon', [function() { return [-.5, y2.Y()]; }, function() { return [2.5, y2.Y()]; },
function() { return [2.5, y3.Y()]; }, function() { return [-.5, y3.Y()]; }],
{ fillColor : '#bd4444', fillOpacity : .3, highlight : false, vertices : { visible : false }, borders : { visible : false }});
var h1 = board.create('segment', [function() { return x1; }, function() { return z1; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var h2 = board.create('segment', [function() { return [z2.X(), 0]; },
function() { return [z2.X(), 8]}], { strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var h3 = board.create('segment', [function() { return [z3.X(), 0]; },
function() { return [z3.X(), 8]}], { strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var delta = board.create('polygon', [h2.point1, h2.point2, h3.point2, h3.point1],
{ fillColor : '#446abd', fillOpacity : .3, highlight : false, vertices : { visible : false }, borders : { visible : false }});
var txt = board.create('text', [-2.5, .7, function() {
return '
', size : 2, strokeColor : 'black', strokeWidth : .5, fillColor : '#bd4444',
showinfobox : false, highlight : false,
label : { useMathJax : true, strokeColor : '#bd4444', offset : [5, 25] }});
var y2 = board.create('point', [0, function(){return f(x1.X())-s.Value();}], { visible : false });
var y3 = board.create('point', [0, function(){return f(x1.X())+s.Value();}], { visible : false });
var z1 = board.create('point', [function(){return y1.Y()/4;}, function(){return y1.Y();}], { visible : false });
var z2 = board.create('point', [function(){return y2.Y()/4;}, function(){return y2.Y();}], { visible : false });
var z3 = board.create('point', [function(){return y3.Y()/4;}, function(){return y3.Y();}], { visible : false });
var v1 = board.create('segment', [z1, y1], { strokeColor : '#bd4444', strokeWidth : 1, highlight : false });
var v2 = board.create('line', [z2, y2], { strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var v3 = board.create('line', [z3, y3], { strokeColor: '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var epsilon = board.create('polygon', [function() { return [-.5, y2.Y()]; }, function() { return [2.5, y2.Y()]; },
function() { return [2.5, y3.Y()]; }, function() { return [-.5, y3.Y()]; }],
{ fillColor : '#bd4444', fillOpacity : .3, highlight : false, vertices : { visible : false }, borders : { visible : false }});
var h1 = board.create('segment', [function() { return x1; }, function() { return z1; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var h2 = board.create('segment', [function() { return [z2.X(), 0]; },
function() { return [z2.X(), 8]}], { strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var h3 = board.create('segment', [function() { return [z3.X(), 0]; },
function() { return [z3.X(), 8]}], { strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var delta = board.create('polygon', [h2.point1, h2.point2, h3.point2, h3.point1],
{ fillColor : '#446abd', fillOpacity : .3, highlight : false, vertices : { visible : false }, borders : { visible : false }});
var txt = board.create('text', [-2.5, .7, function() {
return ' '; }], {
strokeColor : '#446abd', useMathJax : true, fixed : true
});
/*board.unsuspendUpdate();*/
board.fullUpdate();
})();
'; }], {
strokeColor : '#446abd', useMathJax : true, fixed : true
});
/*board.unsuspendUpdate();*/
board.fullUpdate();
})();
Example 4.
Let  . We define a function
. We define a function  by
by
 In Example 2 we saw that this function is not continuous at the point
In Example 2 we saw that this function is not continuous at the point  . To prove this using the
. To prove this using the  -test, we need to find some
-test, we need to find some  and some
and some  such that for all
such that for all  ,
,  , but
, but  .
.
Proof. Let  and
and  . By choosing
. By choosing  , we have
, we have
 and
and
 Therefore by Theorem 5
Therefore by Theorem 5  is not continuous at the point
is not continuous at the point  .
.

 ', strokeWidth : .3, strokeColor : 'black', fillColor : '#446abd', showinfobox : false,
highlight : false, fixed : true,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#446abd' }});
board.suspendUpdate();
var x2 = board.create('point', [ function(){return x1.X()-s.Value();}, 0],
{ visible : false });
var x3 = board.create('point', [function(){return x1.X()+s.Value();},0],
{ visible : false });
var y1 = board.create('point', [-2, function() { return f(x1.X()); }],
{ size : 2, name: '
', strokeWidth : .3, strokeColor : 'black', fillColor : '#446abd', showinfobox : false,
highlight : false, fixed : true,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#446abd' }});
board.suspendUpdate();
var x2 = board.create('point', [ function(){return x1.X()-s.Value();}, 0],
{ visible : false });
var x3 = board.create('point', [function(){return x1.X()+s.Value();},0],
{ visible : false });
var y1 = board.create('point', [-2, function() { return f(x1.X()); }],
{ size : 2, name: ' ', strokeWidth : .3, strokeColor : 'black', fillColor : '#446abd', showinfobox : false,
highlight : false,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#446abd' } });
var yd = board.create('point', [-2, function() { return f(x2.X()); }], {
size : 2, name: '
', strokeWidth : .3, strokeColor : 'black', fillColor : '#446abd', showinfobox : false,
highlight : false,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#446abd' } });
var yd = board.create('point', [-2, function() { return f(x2.X()); }], {
size : 2, name: ' ', strokeWidth : .3, strokeColor : 'black', fillColor : '#bd4444', showinfobox : false,
highlight : false,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#bd4444' }
});
/* doesn't really do anything atm... */
var dist = function() { if (Math.abs(f(x1)-f(x2.X())) != 0 || Math.abs(f(x1)-f(x3.X())) != 0) { return .5; } else { return 0; } };
var y2 = board.create('point', [0, function() {
return y1.Y()-dist(); }],
{ visible : false });
var y3 = board.create('point', [0, function() {
return y1.Y()+dist(); }],
{ visible : false });
var endpoint1 = board.create('point', [0, 2],
{ name : '', fixed : true, size : 2, fillColor : 'white', strokeWidth : .5, strokeColor : 'black', showinfobox : false });
var endpoint2 = board.create('point', [0, 3],
{ name : '', fixed : true, size : 2, fillColor : 'black', strokeWidth : .5, strokeColor : 'black', showinfobox : false });
var v1 = board.create('segment', [x1, function() { return [x1.X(), y1.Y()]; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var v2 = board.create('line', [x2, function() { return [x2.X(), x2.Y()+1]; }],
{ strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var v3 = board.create('line', [x3, function() { return [x3.X(), x3.Y()+1]; }],
{ strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var delta = board.create('polygon', [function() { return [x2.X(), -5]; }, function() { return [x2.X(), 6]; },
function() { return [x3.X(), 6]; }, function() { return [x3.X(), -5]; }], {
highlight : false, fixed : true, vertices : { visible : false }, borders : { visible : false }, fillColor : '#446abd',
fillOpacity : .2
});
var h1 = board.create('segment', [y1, function() { return [x1.X(), y1.Y()]; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var h2 = board.create('line', [function() { return y2; }, function() { return [y2.X()+1, y2.Y()]; }],
{ strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var h3 = board.create('line', [function() { return y3; }, function() { return [y3.X()+1, y3.Y()]; }],
{ strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var epsilon = board.create('polygon', [[-5, 3.5],[10, 3.5],[10, 2.5], [-5, 2.5]], {
highlight : false, fixed : true, vertices : { visible : false }, borders : { visible : false }, fillColor : '#bd4444',
fillOpacity : .2
});
var txt = board.create('text', [4.2, -1.5, function() {
return '
', strokeWidth : .3, strokeColor : 'black', fillColor : '#bd4444', showinfobox : false,
highlight : false,
label : { useMathJax : true, offset : [5, 25], strokeColor : '#bd4444' }
});
/* doesn't really do anything atm... */
var dist = function() { if (Math.abs(f(x1)-f(x2.X())) != 0 || Math.abs(f(x1)-f(x3.X())) != 0) { return .5; } else { return 0; } };
var y2 = board.create('point', [0, function() {
return y1.Y()-dist(); }],
{ visible : false });
var y3 = board.create('point', [0, function() {
return y1.Y()+dist(); }],
{ visible : false });
var endpoint1 = board.create('point', [0, 2],
{ name : '', fixed : true, size : 2, fillColor : 'white', strokeWidth : .5, strokeColor : 'black', showinfobox : false });
var endpoint2 = board.create('point', [0, 3],
{ name : '', fixed : true, size : 2, fillColor : 'black', strokeWidth : .5, strokeColor : 'black', showinfobox : false });
var v1 = board.create('segment', [x1, function() { return [x1.X(), y1.Y()]; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var v2 = board.create('line', [x2, function() { return [x2.X(), x2.Y()+1]; }],
{ strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var v3 = board.create('line', [x3, function() { return [x3.X(), x3.Y()+1]; }],
{ strokeColor : '#446abd', dash : 2, strokeWidth : 1, highlight : false });
var delta = board.create('polygon', [function() { return [x2.X(), -5]; }, function() { return [x2.X(), 6]; },
function() { return [x3.X(), 6]; }, function() { return [x3.X(), -5]; }], {
highlight : false, fixed : true, vertices : { visible : false }, borders : { visible : false }, fillColor : '#446abd',
fillOpacity : .2
});
var h1 = board.create('segment', [y1, function() { return [x1.X(), y1.Y()]; }],
{ strokeColor : '#446abd', strokeWidth : 1, highlight : false });
var h2 = board.create('line', [function() { return y2; }, function() { return [y2.X()+1, y2.Y()]; }],
{ strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var h3 = board.create('line', [function() { return y3; }, function() { return [y3.X()+1, y3.Y()]; }],
{ strokeColor : '#bd4444', dash : 2, strokeWidth : 1, highlight : false });
var epsilon = board.create('polygon', [[-5, 3.5],[10, 3.5],[10, 2.5], [-5, 2.5]], {
highlight : false, fixed : true, vertices : { visible : false }, borders : { visible : false }, fillColor : '#bd4444',
fillOpacity : .2
});
var txt = board.create('text', [4.2, -1.5, function() {
return ' '/*Math.max(Math.abs(y2.Y() - y1.Y()), Math.abs(y1.Y() - y3.Y())).toFixed(2)*/;
}], { strokeColor: '#bd4444', useMathJax : true, fixed : true });
board.unsuspendUpdate();
board.fullUpdate();
})();
'/*Math.max(Math.abs(y2.Y() - y1.Y()), Math.abs(y1.Y() - y3.Y())).toFixed(2)*/;
}], { strokeColor: '#bd4444', useMathJax : true, fixed : true });
board.unsuspendUpdate();
board.fullUpdate();
})();
Properties of continuous functions
This section contains some fundamental properties of continuous functions. We start with the Intermediate Value Theorem for continuous functions, also known as Bolzano's Theorem. This theorem states that a function that is continuous on a given (closed) real interval, attains all values between its values at endpoints of the interval. Intuitively, this follows from the fact that the graph of a function defined on a real interval is a continuous curve.
The Intermediate Value Theorem.
Example 1.
Let function  , where
, where
 Show that there is at least one
Show that there is at least one  such that
such that  .
.
Solution. As a polynomial function,  is continuous. And because
is continuous. And because
 and
and
 by the Intermediate Value Theorem there is at least one
by the Intermediate Value Theorem there is at least one ![c \in ]-1, 1[ c \in ]-1, 1[](https://mycourses.aalto.fi/filter/tex/pix.php/1d1e7e33b0ebb4086ca0cfea832f3789.gif) such that
such that  .
.
Example 2.
By the Intermediate Value Theorem we have  for
for  or
or  . Similarly,
. Similarly,  for
for  or
or  , because:
, because:
 '}], { strokeColor : 'black', fontSize : 13, fixed : true });
var fright = board.create('text', [9.1, 7.6, function() { return '
'}], { strokeColor : 'black', fontSize : 13, fixed : true });
var fright = board.create('text', [9.1, 7.6, function() { return ' '}], { strokeColor : 'black', fontSize : 13, fixed : true });
var xleft = board.create('text', [1.1, -.1, function() { return '
'}], { strokeColor : 'black', fontSize : 13, fixed : true });
var xleft = board.create('text', [1.1, -.1, function() { return ' ' }], { strokeColor : 'black', fontSize : 13, fixed : true });
var xright = board.create('text', [9.1, -.1, function() { return '
' }], { strokeColor : 'black', fontSize : 13, fixed : true });
var xright = board.create('text', [9.1, -.1, function() { return ' ' }], { strokeColor : 'black', fontSize : 13, fixed : true });
l.on('drag', function() {
if(l.point1.Y() >= 7) {
l.point1.moveTo([0, 7]);
l.point2.moveTo([1, 7]);
}
else if(l.point1.Y() <= 4) {
l.point1.moveTo([0, 4]);
l.point2.moveTo([1, 4]);
}
});
var intersections = [];
intersections[0] = board.create('intersection', [l, g, 0], { name : '
' }], { strokeColor : 'black', fontSize : 13, fixed : true });
l.on('drag', function() {
if(l.point1.Y() >= 7) {
l.point1.moveTo([0, 7]);
l.point2.moveTo([1, 7]);
}
else if(l.point1.Y() <= 4) {
l.point1.moveTo([0, 4]);
l.point2.moveTo([1, 4]);
}
});
var intersections = [];
intersections[0] = board.create('intersection', [l, g, 0], { name : ' ', showinfobox : false,
label : { fontSize : 13, offset : [0, -15], strokeColor : 'blue', strokeWidth : .5} });
intersections[1] = board.create('intersection', [l, g, 1], { name : '
', showinfobox : false,
label : { fontSize : 13, offset : [0, -15], strokeColor : 'blue', strokeWidth : .5} });
intersections[1] = board.create('intersection', [l, g, 1], { name : ' ', showinfobox : false,
label : { fontSize : 13, offset : [8, 22], strokeColor : 'blue', strokeWidth : .5} });
intersections[2] = board.create('intersection', [l, g, 2], { name : '
', showinfobox : false,
label : { fontSize : 13, offset : [8, 22], strokeColor : 'blue', strokeWidth : .5} });
intersections[2] = board.create('intersection', [l, g, 2], { name : ' ', showinfobox : false,
label : { fontSize : 13, offset : [0, -15], strokeColor : 'blue', strokeWidth : .5} });
board.unsuspendUpdate();
})();
/* Example 1. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox17', {
boundingbox : [-3.5, 2.5, 3.5, -3.5],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return (Math.pow(x,5)-3*x-1); }
board.create('functiongraph', [f, -3.5, 3.5], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.fullUpdate();
})();
/* Example 2. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox18', {
boundingbox : [-3.2, 2.9, 3.2, -2.9],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return (x*x*x-x); }
board.create('functiongraph', [f, -3.2, -1], {
strokeColor : 'blue',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, -1, 0], {
strokeColor : 'red',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, 0, 1], {
strokeColor : 'blue',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, 1, 3.2], {
strokeColor : 'red',
strokeWidth : 2,
highlight : false
});
board.fullUpdate();
})();
', showinfobox : false,
label : { fontSize : 13, offset : [0, -15], strokeColor : 'blue', strokeWidth : .5} });
board.unsuspendUpdate();
})();
/* Example 1. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox17', {
boundingbox : [-3.5, 2.5, 3.5, -3.5],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return (Math.pow(x,5)-3*x-1); }
board.create('functiongraph', [f, -3.5, 3.5], {
strokeColor : 'black',
strokeWidth : 2,
highlight : false
});
board.fullUpdate();
})();
/* Example 2. */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox18', {
boundingbox : [-3.2, 2.9, 3.2, -2.9],
showcopyright : false,
shownavigation : false});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
ticks : { majorHeight : 7, minorTicks : 0, drawZero : true }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return (x*x*x-x); }
board.create('functiongraph', [f, -3.2, -1], {
strokeColor : 'blue',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, -1, 0], {
strokeColor : 'red',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, 0, 1], {
strokeColor : 'blue',
strokeWidth : 2,
highlight : false
});
board.create('functiongraph', [f, 1, 3.2], {
strokeColor : 'red',
strokeWidth : 2,
highlight : false
});
board.fullUpdate();
})();
Next we prove that a continuous function defined on a closed real interval is necessarily bounded. For this result, it is important that the interval is closed. A counter example for an open interval is given after the next theorem.
Example 4.
Example 5.
Let ![f:[-1,2] \to \mathbb{R} f:[-1,2] \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/46f6b5865e82341801d84f074d5275a9.gif) , where
, where
 The domain of the function is
The domain of the function is ![[-1,2] [-1,2]](https://mycourses.aalto.fi/filter/tex/pix.php/939b17134a44bb821e6c01efd044b32e.gif) . To determine the range of the function, we first notice that the function is decreasing. We will now show this.
. To determine the range of the function, we first notice that the function is decreasing. We will now show this.
Because  ,
,
 and
and
 Thus, if
Thus, if  then
then  , which means that the function
, which means that the function  is decreasing.
is decreasing.
We know that a decreasing function has its minimum value in the right endpoint of the interval. Thus, the minimum value of ![f:[-1,2] \to \mathbb{R} f:[-1,2] \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/46f6b5865e82341801d84f074d5275a9.gif) is
is
 Respectively, a decreasing function has it's maximum value in the left endpoint of the interval and so the maximum value of
Respectively, a decreasing function has it's maximum value in the left endpoint of the interval and so the maximum value of ![f:[-1,2] \to \mathbb{R} f:[-1,2] \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/46f6b5865e82341801d84f074d5275a9.gif) is
is

As a polynomial function,  is continuous and it therefore has all the values between it's minimum and maximum values. Hence, the range of
is continuous and it therefore has all the values between it's minimum and maximum values. Hence, the range of  is
is ![[-7, 5] [-7, 5]](https://mycourses.aalto.fi/filter/tex/pix.php/e8699196563455925f438ba7d4253294.gif) .
.
Example 6.
Suppose that  is a polynomial. Then
is a polynomial. Then  is continuous on
is continuous on  and, by Theorem 7,
and, by Theorem 7,  is bounded on every closed interval
is bounded on every closed interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) ,
,  . Furthermore, by Theorem 3,
. Furthermore, by Theorem 3,  must have minimum and maximum values on
must have minimum and maximum values on ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) .
.
Note. Theorem 8 is connected to the Intermediate Value Theorem in the following way:
4. Derivative
Derivative
The definition of the derivative of a function is given next. We start with an example illustrating the idea behind the formal definition.
Example 0.
The graph below shows how far a cyclist gets from his starting point.
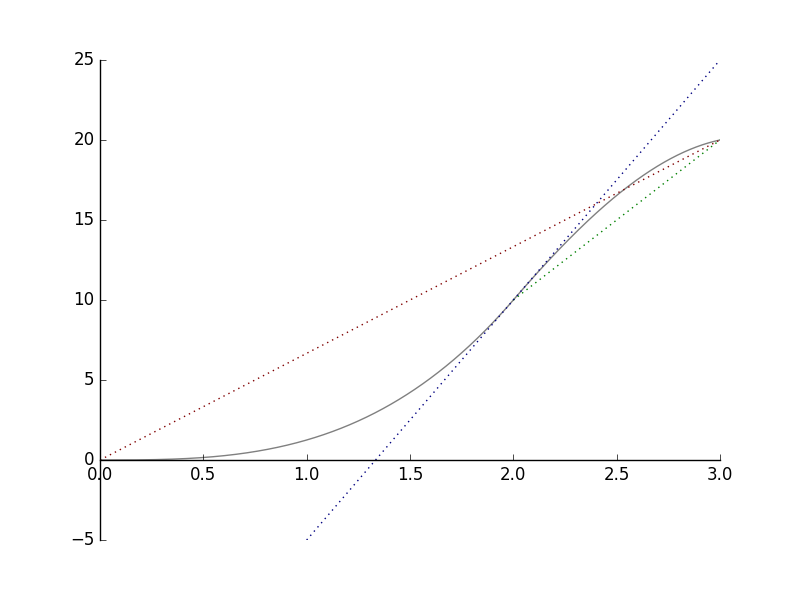
a) Look at the red line. We can see that in three hours, the cyclist moved  km. The average speed of the whole trip is
km. The average speed of the whole trip is  km/h.
km/h.
b) Now look at the green line. We can see that during the third hour the cyclist moved  km further. That makes the average speed of that time interval
km further. That makes the average speed of that time interval  km/h.
km/h.
Notice that the slope of the red line is  and that the slope of the blue line is
and that the slope of the blue line is  . These are the same values as the corresponding average speeds.
. These are the same values as the corresponding average speeds.
c) Look at the blue line. It is the tangent of the curve at the point  . Using the same principle as with average speeds, we conclude that after two hours of the departure, the speed of the cyclist was
. Using the same principle as with average speeds, we conclude that after two hours of the departure, the speed of the cyclist was  km/h
km/h  km/h.
km/h.
Now we will proceed to the general definition:
Definition: Derivative
Let  . The derivative of function
. The derivative of function  at the point
at the point  is
is  If
If  exists, then
exists, then  is said to be differentiable at the point
is said to be differentiable at the point  .
.
Note: Since  , then
, then  , and thus the definition can also be written in the form
, and thus the definition can also be written in the form 
Interpretation. Consider the curve  . Now if we draw a line through the points
. Now if we draw a line through the points  and
and  , we see that the slope of this line is
, we see that the slope of this line is  When
When  , the line intersects with the curve
, the line intersects with the curve  only in the point
only in the point  . This line is the tangent of the curve
. This line is the tangent of the curve  at the point
at the point  and its slope is
and its slope is  which is the derivative of the function
which is the derivative of the function  at
at  . Hence, the tangent is given by the equation
. Hence, the tangent is given by the equation 
Interactivity. Move the point of intersection and observe changes on the tangent line of the curve.
Example 2.
Let  be the function
be the function  . We find the derivative of
. We find the derivative of  .
.
Immediately from the definition we get: ![\begin{aligned}f'(x) &=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to 0} \frac{[a(x+h)+b]-[ax+b]}{h} \\ &=\lim_{h\to 0} a \\ &=a.\end{aligned} \begin{aligned}f'(x) &=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to 0} \frac{[a(x+h)+b]-[ax+b]}{h} \\ &=\lim_{h\to 0} a \\ &=a.\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/5af936863c453fd1ea52d94c4e9b5344.gif)
Here  is the slope of the tangent line. Note that the derivative at
is the slope of the tangent line. Note that the derivative at  does not depend on
does not depend on  because
because  is the equation of a line.
is the equation of a line.
Note. When  , we get
, we get  and
and  . The derivative of a constant function is zero.
. The derivative of a constant function is zero.
Example 3.
Let  be the function
be the function  . Does
. Does  have a derivative at
have a derivative at  ?
?
The graph  has no tangent at the point
has no tangent at the point  :
:  Thus
Thus  does not exist.
does not exist.
Conclusion. The function  is not differentiable at the point
is not differentiable at the point  .
.
Remark. Let  . If
. If  exists for every
exists for every  then we get a function
then we get a function  . We write:
. We write:
| (1) |  |
=  , , |
|
| (2) |  |
=  |
=  , , |
| (3) |  |
=  |
=  , , |
| (4) |  |
=  |
=  , , |
| ... |
Here  is called the second derivative of
is called the second derivative of  at
at  ,
,  is the third derivative, and so on.
is the third derivative, and so on.
We introduce the notation \begin{eqnarray} C^n\bigl( ]a,b[\bigr) =\{ f\colon \, ]a,b[\, \to \mathbb{R} & \mid & f \text{ is } n \text{ times differentiable on the interval } ]a,b[ \nonumber \\ & & \text{ and } f^{(n)} \text{ is continuous}\}. \nonumber \end{eqnarray} These functions are said to be n times continuously differentiable.
Example 4.
The distance moved by a cyclist (or a car) is given by  . Then the speed at the moment
. Then the speed at the moment  is
is  and the acceleration is
and the acceleration is  .
.
Linearization and differential
 where the right-handed side is the linearization or the differential of
where the right-handed side is the linearization or the differential of  at
at  . The differential is denoted by
. The differential is denoted by  . The graph of the linearization,
. The graph of the linearization,  is the tangent line drawn on the graph of the function
is the tangent line drawn on the graph of the function  at the point
at the point  . Later, in multi-variable calculus, the true meaning of the differential becomes clear. For now, it is not necessary to get troubled by the details.
. Later, in multi-variable calculus, the true meaning of the differential becomes clear. For now, it is not necessary to get troubled by the details.
Properties of derivative
Next we give some useful properties of the derivative. These properties allow us to find derivatives for some familiar classes of functions such as polynomials and rational functions.
Continuity and derivative
If  is differentiable at the point
is differentiable at the point  , then
, then  is continuous at the point
is continuous at the point  :
:  Why? Because if
Why? Because if  is differentiable, then we get
is differentiable, then we get  as
as  .
.
Note. If a function is continuous at the point  , it doesn't have to be differentiable at that point. For example, the function
, it doesn't have to be differentiable at that point. For example, the function  is continuous, but not differentiable at the point
is continuous, but not differentiable at the point  .
.
Differentiation Rules
For  we repeteadly apply the product rule, and obtain
we repeteadly apply the product rule, and obtain 
The case of negative  is obtained from this and the product rule applied to the identity
is obtained from this and the product rule applied to the identity  .
.
From the power rule we obtain a formula for the derivative of a polynomial. Let  where
where  . Then
. Then 
Suppose that  is differentiable at
is differentiable at  and
and  . We determine
. We determine 
From the definition we obtain: 
Example 3.
The one-sided limits of the difference quotient have different signs at a local extremum. For example, for a local maximum it holds that \begin{eqnarray} \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative} }{\text{positive}}&\le& 0, \text{ when } h>0, \nonumber \\ \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative}}{\text{negative}}&\ge& 0, \text{ when } h<0 \nonumber \end{eqnarray} and  is so small that
is so small that  is a maximum on the interval
is a maximum on the interval ![[x_0-h,x_0+h] [x_0-h,x_0+h]](https://mycourses.aalto.fi/filter/tex/pix.php/fa82e5aaac1e1a7465724ab32e282839.gif) .
.
Derivatives of Trigonometric Functions
In this section, we give differentiation formulas for trigonometric functions  ,
,  and
and  .
.
The Chain Rule
In this section we learn a formula for finding the derivative of a composite function. This important formula is known as the Chain Rule.
The Chain Rule.
Proof.Example 1.
Example 2.
Example 3.
Extremal Value Problems
We will discuss the Intermediate Value Theorem for differentiable functions, and its connections to extremal value problems.
Definition: Local Maxima and Minima
A function  has a a local maximum at the point
has a a local maximum at the point  , if for some
, if for some  and for all
and for all  such that
such that  , we have
, we have  .
.
Similarly, a function  has a local minimum at the point
has a local minimum at the point  , if for some
, if for some  and for all
and for all  such that
such that  , we have
, we have  .
.
A local extreme is a local maximum or a local minimum.
Remark. If  is a local maximum value and
is a local maximum value and  exists, then
exists, then
 Hence
Hence  .
.
We get:
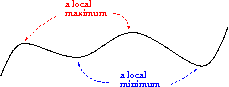
Example 1.
Let  be defined by
be defined by
 Then
Then
 and we can see that at the points
and we can see that at the points  and
and  the local maximum and minimum of
the local maximum and minimum of  are obtained,
are obtained,

Finding the global extrema
In practice, when we are looking for the local extrema of a given function, we need to check three kinds of points:
the zeros of the derivative
the endpoints of the domain of definition (interval)
points where the function is not differentiable
If we happened to know beforehand that the function has a minimum/maximum, then we start off by finding all the possible local extrema (the points described above), evaluate the function at these points and pick the greatest/smallest of these values.
Example 2.
Let us find the smallest and greatest value of the function ![f\colon [0,2]\to \mathbf{R} f\colon [0,2]\to \mathbf{R}](https://mycourses.aalto.fi/filter/tex/pix.php/ee77c8a9721b9494f327d61422eb2068.gif) ,
,  . Since the function is continuous on a closed interval, then it has a maximum and a minimum. Since the function is differentiable, it is sufficient to examine the endpoints of the interval and the zeros of the derivative that are contained in the interval.
. Since the function is continuous on a closed interval, then it has a maximum and a minimum. Since the function is differentiable, it is sufficient to examine the endpoints of the interval and the zeros of the derivative that are contained in the interval.
The zeros of the derivative:  .
Since
.
Since ![-\sqrt{2}\not\in [0,2] -\sqrt{2}\not\in [0,2]](https://mycourses.aalto.fi/filter/tex/pix.php/601d5044bf746b9e7af4678c2c3463a1.gif) , we only need to evaluate the function at three points,
, we only need to evaluate the function at three points,  ,
,  and
and  . From these we can see that the smallest value of the function is
. From these we can see that the smallest value of the function is  and the greatest value is
and the greatest value is  , respectively.
, respectively.
Next we will formulate a fundamental result for differentiable functions. The basic idea here is that the change on an interval can only happen, if there is change at some point on the inverval.
Theorem 2.
(The Intermediate Value Theorem for Differentiable Functions). Let ![f\colon [a,b]\to \mathbb{R} f\colon [a,b]\to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/fb88b7c4cd82a1b35ba68754b552ae78.gif) be continuous in the interval
be continuous in the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) and differentiable in the interval
and differentiable in the interval  . Then
. Then
 for some
for some 
Let  be continuous in the interval
be continuous in the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) and differentiable in the interval
and differentiable in the interval  . Let us define
. Let us define

Now  and
and  is differentiable in the interval
is differentiable in the interval  . According to Rolle's Theorem, there exists
. According to Rolle's Theorem, there exists  such that
such that  . Hence
. Hence

This result has an important application:
Theorem 3.
Example 3.
Example 4.
We need to find a rectangle so that its area is  and it has the least possible perimeter.
and it has the least possible perimeter.
Let  and
and  be the sides of the rectangle. Then
be the sides of the rectangle. Then  and we get
and we get  . Now the perimeter is
. Now the perimeter is
 In which point does the function
In which point does the function  get its minimum value? Function
get its minimum value? Function  is continuous and differentiable, when
is continuous and differentiable, when  and using the quotient rule, we get
and using the quotient rule, we get
 Now
Now  , when
, when
 but we have defined that
but we have defined that  and therefore are only interested in the case
and therefore are only interested in the case  . Let's draw a table:
. Let's draw a table:
 |
 |
|
|---|---|---|
 |
 |
 |
 |
decr. | incr. |
As the function  is continuous, we now know that it attains its minimum at the point
is continuous, we now know that it attains its minimum at the point  . Now we calculate the other side of the rectangle:
. Now we calculate the other side of the rectangle:  .
.
Thus, the rectangle, which has the least possible perimeter is actually a square, which sides are of the length  .
.
Example 5.
We must make a one litre measure, which is shaped as a right circular cylinder without a lid. The problem is to find the best size of the bottom and the height so that we need the least possible amount of material to make the measure.
Let  be the radius and
be the radius and  the height of the cylinder. The volume of the cylinder is
the height of the cylinder. The volume of the cylinder is  dm
dm and we can write
and we can write  from which we get
from which we get

The amount of material needed is the surface area

Let function  be defined by
be defined by
 We must find the minimum value for function
We must find the minimum value for function  , which is continuous and differentiable, when
, which is continuous and differentiable, when  . Using the reciprocal rule, we get
. Using the reciprocal rule, we get
 Now
Now  , when
, when
![\begin{aligned}2\pi r^3 - 2 &= 0 \\
2\pi r^3 &= 2 \\
r^3 &= \frac{1}{\pi} \\
r &= \frac{1}{\sqrt[3]{\pi}}.\end{aligned} \begin{aligned}2\pi r^3 - 2 &= 0 \\
2\pi r^3 &= 2 \\
r^3 &= \frac{1}{\pi} \\
r &= \frac{1}{\sqrt[3]{\pi}}.\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/ffb8cf82115510a023a5408e30bf2b57.gif)
Let's draw a table:
 |
![r>\frac{1}{\sqrt[3]{\pi}} r>\frac{1}{\sqrt[3]{\pi}}](https://mycourses.aalto.fi/filter/tex/pix.php/70296efeaa006fb5cd9c2f29b5d0a0e2.gif) |
|
|---|---|---|
 |
 |
 |
 |
decr. | incr. |
As the function  is continuous, we now know that it gets its minimum value at the point
is continuous, we now know that it gets its minimum value at the point ![r= \frac{1}{\sqrt[3]{\pi}} \approx 0.683 r= \frac{1}{\sqrt[3]{\pi}} \approx 0.683](https://mycourses.aalto.fi/filter/tex/pix.php/ef4b63276241174d0f518a6b4301d081.gif) . Then
. Then
![h = \frac{1}{\pi r^2} = \frac{1}{\pi \left(\frac{1}{\sqrt[3]{\pi}}\right)^2} = \frac{1}{\frac{\pi}{\pi^{2/3}}} = \frac{1}{\sqrt[3]{\pi}} \approx 0.683. h = \frac{1}{\pi r^2} = \frac{1}{\pi \left(\frac{1}{\sqrt[3]{\pi}}\right)^2} = \frac{1}{\frac{\pi}{\pi^{2/3}}} = \frac{1}{\sqrt[3]{\pi}} \approx 0.683.](https://mycourses.aalto.fi/filter/tex/pix.php/8af221027cf46db4d652e5781ac056d2.gif)
This means that it would take least materials to make a measure, which is approximately  dm
dm  dm
dm  cm in diameter and
cm in diameter and  dm
dm  cm high.
cm high.
 ',
label : { strokeColor : 'blue' }
});
var t = board.create('tangent', [g1], {
strokeWidht : 2,
strokeOpacity : .8
});
var text1 = board.create('text', [-4, 5, function() { return '
',
label : { strokeColor : 'blue' }
});
var t = board.create('tangent', [g1], {
strokeWidht : 2,
strokeOpacity : .8
});
var text1 = board.create('text', [-4, 5, function() { return ' '}], {
useMathJax : true,
fontSize : 14,
strokeColor : 'black'
});
var text2 = board.create('text', [-4, 4, function() {
var k = t.getSlope();
var b = g1.Y()-k*g1.X();
var temp = '';
if(k == 0) {
temp = '
'}], {
useMathJax : true,
fontSize : 14,
strokeColor : 'black'
});
var text2 = board.create('text', [-4, 4, function() {
var k = t.getSlope();
var b = g1.Y()-k*g1.X();
var temp = '';
if(k == 0) {
temp = ' ';
} else {
if(b < 0) {
temp = '
';
} else {
if(b < 0) {
temp = ' ';
} else {
temp = '
';
} else {
temp = ' ';
}
}
return temp;
}
], {
useMathJax : true,
fontSize : 14,
strokeColor : 'blue'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox : [-3.5, 3, 3.5, -3],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0],[1, 0]], {
ticks : { majorHeight : 5 }
});
var yaxis = board.create('axis' ,[[0, 0],[0, 1]], {
ticks : { majorHeight : 5}
});
var f = function(x) { return x*x*x+1; }
var graph = board.create('functiongraph', [f, -3.5, 3.5], {
strokeWidth : 1.5,
strokeColor : 'black'
});
var g1 = board.create('glider', [1, f(1), graph], { strokeColor : 'black', size : 2, fillColor : 'red', name : '' });
var t = board.create('tangent', [g1], { strokeColor : 'red', strokeWidth : 1.5 });
var a = board.create('segment', [[function() { return g1.X() }, function() { return g1.Y()-t.getSlope(); }],
[function() { return g1.X()-1; }, function() { return g1.Y()-t.getSlope() }]], {
strokeWidth : 2,
strokeOpacity : .8,
dash : 1,
highlight : false
});
var b = board.create('segment', [[ function() { return g1.X(); }, function() { return g1.Y(); }],
[ function() { return a.point1.X(); }, function() { return a.point1.Y(); } ]], {
strokeWidth : 2,
strokeOpacity : .8,
dash : 1,
highlight : false
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox04', {
boundingbox : [-5, 5, 5, -2],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return Math.abs(x); }
board.create('functiongraph', [f, -5, 5], {
strokeWidth : 2,
strokeColor : '#2183de',
highlight : false
});
board.create('text', [1.5, 1.2, function() { return '
';
}
}
return temp;
}
], {
useMathJax : true,
fontSize : 14,
strokeColor : 'blue'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox : [-3.5, 3, 3.5, -3],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0],[1, 0]], {
ticks : { majorHeight : 5 }
});
var yaxis = board.create('axis' ,[[0, 0],[0, 1]], {
ticks : { majorHeight : 5}
});
var f = function(x) { return x*x*x+1; }
var graph = board.create('functiongraph', [f, -3.5, 3.5], {
strokeWidth : 1.5,
strokeColor : 'black'
});
var g1 = board.create('glider', [1, f(1), graph], { strokeColor : 'black', size : 2, fillColor : 'red', name : '' });
var t = board.create('tangent', [g1], { strokeColor : 'red', strokeWidth : 1.5 });
var a = board.create('segment', [[function() { return g1.X() }, function() { return g1.Y()-t.getSlope(); }],
[function() { return g1.X()-1; }, function() { return g1.Y()-t.getSlope() }]], {
strokeWidth : 2,
strokeOpacity : .8,
dash : 1,
highlight : false
});
var b = board.create('segment', [[ function() { return g1.X(); }, function() { return g1.Y(); }],
[ function() { return a.point1.X(); }, function() { return a.point1.Y(); } ]], {
strokeWidth : 2,
strokeOpacity : .8,
dash : 1,
highlight : false
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox04', {
boundingbox : [-5, 5, 5, -2],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var f = function(x) { return Math.abs(x); }
board.create('functiongraph', [f, -5, 5], {
strokeWidth : 2,
strokeColor : '#2183de',
highlight : false
});
board.create('text', [1.5, 1.2, function() { return ' '; }], {
useMathJax : true,
strokeColor : '#2183de',
fontSize : 13,
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox05', {
boundingbox : [-1.7, 10.1, 1.7, -10.1],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 5; };
var f = function(x) { return (x*x*x*x-2)*(2*x+1); }
board.create('functiongraph', [f, -1.7, 1.7], {
strokeWidth : 2.5,
strokeColor : 'black',
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox06', {
boundingbox : [-6.1, 6.5, 6.1, -6.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return x*x*x/(1+x*x); }
board.create('functiongraph', [f, -6.1, 6.1], {
strokeWidth : 2.5,
strokeColor : 'black',
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox07', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.sin(x); }
var df = function(x) { return Math.cos(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'red'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox08', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.cos(x); }
var df = function(x) { return Math.sin(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox09', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.tan(x); }
var df = function(x) { return 1/Math.pow(Math.cos(x),2); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'green'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox10', {
boundingbox : [-3.2, 4.5, 4.8, -2.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(2*x*x-1, 3); }
var df = function(x) { return 6*Math.pow(2*x*x-1, 2); }
board.create('functiongraph', [f, 0, 4.8], {
strokeWidth : 1.5,
strokeColor : 'green'
});
board.create('functiongraph', [df, 0, 4.8], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox11', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.sin(3*x); }
var df = function(x) { return 3*Math.cos(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'red'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox12', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(Math.cos(2*x), 3); }
var df = function(x) { return -6*Math.sin(2*x)*Math.pow(Math.cos(2*x), 2); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox13', {
boundingbox : [-4.73, 4.2, 4.73, -4.2],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return x*x*x-3*x+1; }
var df = function(x) { return 3*x*x-3; }
board.create('functiongraph', [f, -3.2, 3.2], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -3.2, 3.2], {
strokeWidth : 1.5,
strokeColor : 'red'
});
var p = [];
p[0] = board.create('point', [-1, f(-1)]);
p[1] = board.create('point', [-1, df(-1)]);
p[2] = board.create('point', [1, f(1)]);
p[3] = board.create('point', [1, df(1)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
strokeColor : 'black',
size : .5,
name : '',
fillColor : 'black',
fixed : true
});
}
board.create('segment', [p[0],p[1]], {
strokeColor : 'black',
dash : 1,
highlight : false
});
board.create('segment', [p[2],p[3]], {
strokeColor : 'black',
dash : 1,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox14', {
boundingbox : [-6.76, 1, 6.76, -11],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(x, 4)/4-2*x*x-7; }
board.create('functiongraph', [f, -5.6, 5.6], {
strokeWidth : 1.5,
strokeColor : 'black'
});
var p = [];
p[0] = board.create('point', [-2, 0], {
});
p[1] = board.create('point', [-2, f(-2)], {
});
p[2] = board.create('point', [0, 0], {
});
p[3] = board.create('point', [0, f(0)], {
});
p[4] = board.create('point', [2, 0], {
});
p[5] = board.create('point', [2, f(2)], {
});
for(var i=0; i < p.length; i++) {
p[i].setAttribute({ visible : false });
}
board.create('segment', [p[0],p[1]], {
strokeColor : 'red',
highlight : false,
fixed : true
});
board.create('segment', [p[2],p[3]], {
strokeColor : 'blue',
highlight : false,
fixed : true
});
board.create('segment', [p[4],p[5]], {
strokeColor : 'red',
highlight : false,
fixed : true
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox15', {
boundingbox : [-1, 15, 10, -1.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return (2*x*x+18)/x; }
var graph = board.create('functiongraph', [f, -1, 15.9], {
strokeColor : 'black',
strokeWidth : 2.5,
highlight : false
});
var p = [];
p[0] = board.create('point', [3, 0]);
p[1] = board.create('point', [3,f(3)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
name : '',
size : 1,
strokeColor : 'black',
strokeWidth : .5,
fixed : true });
}
board.create('segment', [p[0], p[1]], {
dash : 1,
strokeWidth : 2,
strokeColor : 'red',
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox16', {
boundingbox : [-1, 13, 5, -1],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return Math.PI*x*x+2/x; }
var graph = board.create('functiongraph', [f, 0, 5], {
strokeColor : 'black',
strokeWidth : 2.5,
highlight : false
});
var p = [];
var a = 1/Math.pow(Math.PI,1/3);
p[0] = board.create('point', [a, 0]);
p[1] = board.create('point', [a, f(a)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
name : '',
size : 1,
strokeColor : 'black',
fixed : true });
}
board.create('segment', [p[0], p[1]], {
dash : 1,
strokeWidth : 2,
strokeColor : 'red',
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox17', {
boundingbox : [-4, 4, 4, -4],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var s = board.create('slider', [[-3.5, 3.5], [-.5, 3.5], [-10, 0, 10]],{
suffixLabel : '
'; }], {
useMathJax : true,
strokeColor : '#2183de',
fontSize : 13,
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox05', {
boundingbox : [-1.7, 10.1, 1.7, -10.1],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 5; };
var f = function(x) { return (x*x*x*x-2)*(2*x+1); }
board.create('functiongraph', [f, -1.7, 1.7], {
strokeWidth : 2.5,
strokeColor : 'black',
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox06', {
boundingbox : [-6.1, 6.5, 6.1, -6.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return x*x*x/(1+x*x); }
board.create('functiongraph', [f, -6.1, 6.1], {
strokeWidth : 2.5,
strokeColor : 'black',
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox07', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.sin(x); }
var df = function(x) { return Math.cos(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'red'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox08', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.cos(x); }
var df = function(x) { return Math.sin(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox09', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.tan(x); }
var df = function(x) { return 1/Math.pow(Math.cos(x),2); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'green'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox10', {
boundingbox : [-3.2, 4.5, 4.8, -2.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(2*x*x-1, 3); }
var df = function(x) { return 6*Math.pow(2*x*x-1, 2); }
board.create('functiongraph', [f, 0, 4.8], {
strokeWidth : 1.5,
strokeColor : 'green'
});
board.create('functiongraph', [df, 0, 4.8], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox11', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.sin(3*x); }
var df = function(x) { return 3*Math.cos(x); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'red'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox12', {
boundingbox : [-6.77, 6, 6.77, -6],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(Math.cos(2*x), 3); }
var df = function(x) { return -6*Math.sin(2*x)*Math.pow(Math.cos(2*x), 2); }
board.create('functiongraph', [f, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -6.77, 6.77], {
strokeWidth : 1.5,
strokeColor : 'black'
});
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox13', {
boundingbox : [-4.73, 4.2, 4.73, -4.2],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return x*x*x-3*x+1; }
var df = function(x) { return 3*x*x-3; }
board.create('functiongraph', [f, -3.2, 3.2], {
strokeWidth : 1.5,
strokeColor : 'blue'
});
board.create('functiongraph', [df, -3.2, 3.2], {
strokeWidth : 1.5,
strokeColor : 'red'
});
var p = [];
p[0] = board.create('point', [-1, f(-1)]);
p[1] = board.create('point', [-1, df(-1)]);
p[2] = board.create('point', [1, f(1)]);
p[3] = board.create('point', [1, df(1)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
strokeColor : 'black',
size : .5,
name : '',
fillColor : 'black',
fixed : true
});
}
board.create('segment', [p[0],p[1]], {
strokeColor : 'black',
dash : 1,
highlight : false
});
board.create('segment', [p[2],p[3]], {
strokeColor : 'black',
dash : 1,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox14', {
boundingbox : [-6.76, 1, 6.76, -11],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
var f = function(x) { return Math.pow(x, 4)/4-2*x*x-7; }
board.create('functiongraph', [f, -5.6, 5.6], {
strokeWidth : 1.5,
strokeColor : 'black'
});
var p = [];
p[0] = board.create('point', [-2, 0], {
});
p[1] = board.create('point', [-2, f(-2)], {
});
p[2] = board.create('point', [0, 0], {
});
p[3] = board.create('point', [0, f(0)], {
});
p[4] = board.create('point', [2, 0], {
});
p[5] = board.create('point', [2, f(2)], {
});
for(var i=0; i < p.length; i++) {
p[i].setAttribute({ visible : false });
}
board.create('segment', [p[0],p[1]], {
strokeColor : 'red',
highlight : false,
fixed : true
});
board.create('segment', [p[2],p[3]], {
strokeColor : 'blue',
highlight : false,
fixed : true
});
board.create('segment', [p[4],p[5]], {
strokeColor : 'red',
highlight : false,
fixed : true
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox15', {
boundingbox : [-1, 15, 10, -1.5],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return (2*x*x+18)/x; }
var graph = board.create('functiongraph', [f, -1, 15.9], {
strokeColor : 'black',
strokeWidth : 2.5,
highlight : false
});
var p = [];
p[0] = board.create('point', [3, 0]);
p[1] = board.create('point', [3,f(3)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
name : '',
size : 1,
strokeColor : 'black',
strokeWidth : .5,
fixed : true });
}
board.create('segment', [p[0], p[1]], {
dash : 1,
strokeWidth : 2,
strokeColor : 'red',
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox16', {
boundingbox : [-1, 13, 5, -1],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 2; };
yaxis.defaultTicks.ticksFunction = function() { return 2; };
var f = function(x) { return Math.PI*x*x+2/x; }
var graph = board.create('functiongraph', [f, 0, 5], {
strokeColor : 'black',
strokeWidth : 2.5,
highlight : false
});
var p = [];
var a = 1/Math.pow(Math.PI,1/3);
p[0] = board.create('point', [a, 0]);
p[1] = board.create('point', [a, f(a)]);
for(var i=0; i < p.length; i++) {
p[i].setAttribute({
name : '',
size : 1,
strokeColor : 'black',
fixed : true });
}
board.create('segment', [p[0], p[1]], {
dash : 1,
strokeWidth : 2,
strokeColor : 'red',
fixed : true,
highlight : false
});
board.fullUpdate();
})();
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox17', {
boundingbox : [-4, 4, 4, -4],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
highlight : false,
drawZero : true,
ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
highlight : false,
ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 1; };
var s = board.create('slider', [[-3.5, 3.5], [-.5, 3.5], [-10, 0, 10]],{
suffixLabel : '  ',
label : { useMathJax : true, fontSize : 13 },
fillColor : '#31d490',
withTicks : false,
precision : 2,
snapWidth : 1
});
var f = function(x) { return x*x*x-x; }
var g = function(x) { return s.Value()*(x*x*x-x); }
var graph1 = board.create('functiongraph', [f, -4, 4], {
strokeColor : '#4260f5',
strokeWidth : 2.5,
highlight : false,
strokeOpacity : 0.6,
highlight : false
});
var graph2 = board.create('functiongraph', [g, -4, 4], {
strokeColor : '#31d490',
strokeWidth : 2.5,
highlight : false,
strokeOpacity : .8,
highlight : false
});
var g0 = board.create('glider', [0, 0, xaxis], {
name : '
',
label : { useMathJax : true, fontSize : 13 },
fillColor : '#31d490',
withTicks : false,
precision : 2,
snapWidth : 1
});
var f = function(x) { return x*x*x-x; }
var g = function(x) { return s.Value()*(x*x*x-x); }
var graph1 = board.create('functiongraph', [f, -4, 4], {
strokeColor : '#4260f5',
strokeWidth : 2.5,
highlight : false,
strokeOpacity : 0.6,
highlight : false
});
var graph2 = board.create('functiongraph', [g, -4, 4], {
strokeColor : '#31d490',
strokeWidth : 2.5,
highlight : false,
strokeOpacity : .8,
highlight : false
});
var g0 = board.create('glider', [0, 0, xaxis], {
name : ' ',
size : 4,
strokeColor : 'black',
strokeWidth : .7,
fillColor : '#42f57e',
label : { useMathJax : true }
});
var g1 = board.create('glider', [0, 0, graph1], {
name : '',
size : 2,
strokeWidth : .7,
strokeColor : 'black',
fillColor : '#42f57e',
fixed : true,
highlight : false
});
var l1 = board.create('line', [g0, g1], {
straightFirst : false,
strokeColor : '#42f57e',
dash : 1,
highlight : false
});
var g2 = board.create('glider', [0, 0, graph2], {
visible : false
});
var t1 = board.create('tangent', [g1], {
strokeColor : '#4260f5',
strokeWidth : 2.5,
strokeOpacity : 0.6,
highlight : false
});
var t2 = board.create('tangent', [g2], {
strokeColor : '#31d490',
strokeWidth : 2.5,
strokeOpacity : .8,
highlight : false
});
board.create('text', [-3.5, 2.8, function() { return '
',
size : 4,
strokeColor : 'black',
strokeWidth : .7,
fillColor : '#42f57e',
label : { useMathJax : true }
});
var g1 = board.create('glider', [0, 0, graph1], {
name : '',
size : 2,
strokeWidth : .7,
strokeColor : 'black',
fillColor : '#42f57e',
fixed : true,
highlight : false
});
var l1 = board.create('line', [g0, g1], {
straightFirst : false,
strokeColor : '#42f57e',
dash : 1,
highlight : false
});
var g2 = board.create('glider', [0, 0, graph2], {
visible : false
});
var t1 = board.create('tangent', [g1], {
strokeColor : '#4260f5',
strokeWidth : 2.5,
strokeOpacity : 0.6,
highlight : false
});
var t2 = board.create('tangent', [g2], {
strokeColor : '#31d490',
strokeWidth : 2.5,
strokeOpacity : .8,
highlight : false
});
board.create('text', [-3.5, 2.8, function() { return ' '; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [-3.5, 2.3, function() { return '
'; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [-3.5, 2.3, function() { return ' '; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [1.5, -2, function() { return '
'; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [1.5, -2, function() { return ' '; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [1.5, -2.5, function() { return '
'; }], {
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
board.create('text', [1.5, -2.5, function() { return ' '; }],{
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
g0.on('drag', function() {
var x = g0.X();
g1.moveTo([x, f(x)]);
g2.moveTo([x, g(x)]);
board.update();
});
board.fullUpdate();
})();
"; }
],
{
fontSize : 15
});*/
board.unsuspendUpdate();
}
}
function addDerivative() {
if (JXG.isFunction(f)) {
board.create('functiongraph',[JXG.Math.Numerics.D(f),
function(){
var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[0,0],board);
return c.usrCoords[1];
},
function(){
var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[board.canvasWidth,0],board);
return c.usrCoords[1];
}], {
dash : 2,
strokeWidth : 2,
strokeColor : '#3ac946'
});
}
}
document.getElementById('plot').onclick = plotter;
document.getElementById('clear all').onclick = clearAll;
document.getElementById('add tangent').onclick = addTangent;
document.getElementById('add Derivative').onclick = addDerivative;
})();
'; }],{
useMathJax : true,
fontSize : 13,
strokeColor : 'black',
fixed : true,
highlight : false
});
g0.on('drag', function() {
var x = g0.X();
g1.moveTo([x, f(x)]);
g2.moveTo([x, g(x)]);
board.update();
});
board.fullUpdate();
})();
"; }
],
{
fontSize : 15
});*/
board.unsuspendUpdate();
}
}
function addDerivative() {
if (JXG.isFunction(f)) {
board.create('functiongraph',[JXG.Math.Numerics.D(f),
function(){
var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[0,0],board);
return c.usrCoords[1];
},
function(){
var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[board.canvasWidth,0],board);
return c.usrCoords[1];
}], {
dash : 2,
strokeWidth : 2,
strokeColor : '#3ac946'
});
}
}
document.getElementById('plot').onclick = plotter;
document.getElementById('clear all').onclick = clearAll;
document.getElementById('add tangent').onclick = addTangent;
document.getElementById('add Derivative').onclick = addDerivative;
})();
5. Taylor polynomial
Taylor polynomial
Definition: Taylor polynomial
Let  be
be  times differentiable at the point
times differentiable at the point  . Then the Taylor polynomial
\begin{align}
P_n(x)&=P_n(x;x_0)\\\
&=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+ \\
& \dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\
&=\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k\\
\end{align}
is the best polynomial approximation of degree
. Then the Taylor polynomial
\begin{align}
P_n(x)&=P_n(x;x_0)\\\
&=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+ \\
& \dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\
&=\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k\\
\end{align}
is the best polynomial approximation of degree  (with respect to the derivative) for a function
(with respect to the derivative) for a function  , close to the point
, close to the point  .
.
Note. The special case  is often called the Maclaurin polynomial.
is often called the Maclaurin polynomial.
If  is
is  times differentiable at
times differentiable at  , then the Taylor polynomial
has the same derivatives at
, then the Taylor polynomial
has the same derivatives at  as the function
as the function  , up to the order
, up to the order  (of the derivative).
(of the derivative).
The reason (case  ): Let
): Let
 so that
\begin{align}
P_n'(x)&=c_1+2c_2x+3c_3x^2+\dots +nc_nx^{n-1}, \\
P_n''(x)&=2c_2+3\cdot 2 c_3x\dots +n(n-1)c_nx^{n-2} \\
P_n'''(x)&=3\cdot 2 c_3\dots +n(n-1)(n-2)c_nx^{n-3} \\
\dots && \\
P^{(k)}(x)&=k!c_k + x\text{ terms} \\
\dots & \\
P^{(n)}(x)&=n!c_n \\
P^{(n+1)}(x)&=0.
\end{align}
so that
\begin{align}
P_n'(x)&=c_1+2c_2x+3c_3x^2+\dots +nc_nx^{n-1}, \\
P_n''(x)&=2c_2+3\cdot 2 c_3x\dots +n(n-1)c_nx^{n-2} \\
P_n'''(x)&=3\cdot 2 c_3\dots +n(n-1)(n-2)c_nx^{n-3} \\
\dots && \\
P^{(k)}(x)&=k!c_k + x\text{ terms} \\
\dots & \\
P^{(n)}(x)&=n!c_n \\
P^{(n+1)}(x)&=0.
\end{align}
From these way we obtain the coefficients one by one:
\begin{align}
c_0= P_n(0)=f(0) &\Rightarrow c_0=f(0) \\
c_1=P_n'(0)=f'(0) &\Rightarrow c_1=f'(0) \\
2c_2=P_n''(0)=f''(0) &\Rightarrow c_2=\frac{1}{2}f''(0) \\
\vdots & \\
k!c_k=P_n^{(k)}(0)=f^{(k)}(0) &\Rightarrow c_k=\frac{1}{k!}f^{(k)}(0). \\
\vdots &\\
n!c_n=P_n^{(n)}(0)=f^{(n)}(0) &\Rightarrow c_k=\frac{1}{n!}f^{(n)}(0).
\end{align}
Starting from index  we cannot pose any new conditions, since
we cannot pose any new conditions, since  .
.
Taylor's Formula
If the derivative  exists and is continuous on
some interval
exists and is continuous on
some interval ![I=\, ]x_0-\delta,x_0+\delta[ I=\, ]x_0-\delta,x_0+\delta[](https://mycourses.aalto.fi/filter/tex/pix.php/80a209f739b80f113803ee7e47c63030.gif) , then
, then
 and the error term
and the error term  satisfies
satisfies
 at some point
at some point ![c\in [x_0,x]\subset I c\in [x_0,x]\subset I](https://mycourses.aalto.fi/filter/tex/pix.php/a6c59d54e8895e424cf74ad41528b3fe.gif) .
If there is a constant
.
If there is a constant  (independent of
(independent of  ) such that
) such that
 for all
for all  , then
, then
 as
as  .
.
\neq omitted here (mathematical induction or integral).
Examples of Maclaurin polynomial approximations: \begin{align} \frac{1}{1-x} &\approx 1+x+x^2+\dots +x^n =\sum_{k=0}^{n}x^k\\ e^x&\approx 1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\dots + \frac{1}{n!}x^n =\sum_{k=0}^{n}\frac{x^k}{k!}\\ \ln (1+x)&\approx x-\frac{1}{2}x^2+\frac{1}{3}x^3-\dots + \frac{(-1)^{n-1}}{n}x^n =\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}x^k\\ \sin x &\approx x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\dots +\frac{(-1)^n}{(2n+1)!}x^{2n+1} =\sum_{k=0}^{n}\frac{(-1)^k}{(2k+1)!}x^{2k+1}\\ \cos x &\approx 1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\dots +\frac{(-1)^n}{(2n)!}x^{2n} =\sum_{k=0}^{n}\frac{(-1)^k}{(2k)!}x^{2k} \end{align}
Example
Which polynomial  approximates the function
approximates the function  in the interval
in the interval
![[-\pi,\pi] [-\pi,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/a5d4b5c6dcadd17bce3289ba1891d927.gif) so that the absolute value of the error is less than
so that the absolute value of the error is less than  ?
?
We use Taylor's Formula for  at
at  . Then
. Then
 independently of
independently of  and the point
and the point  .
Also, in the interval in question, we have
.
Also, in the interval in question, we have  .
The requirement will be satisfied (at least) if
.
The requirement will be satisfied (at least) if
 This inequality must be solved by trying different values of
This inequality must be solved by trying different values of  ; it is
true for
; it is
true for  .
.
The required approximation is achieved with  , which fo sine
is the same as
, which fo sine
is the same as  .
.
Check from graphs:  is not enough, so the theoretical bound is sharp!
is not enough, so the theoretical bound is sharp!
Taylor polynomial and extreme values
If  , then also some higher derivatives may be zero:
, then also some higher derivatives may be zero:
 Then the behaviour of
Then the behaviour of  near
near  is determined by the
leading term (after the constant term
is determined by the
leading term (after the constant term  )
)
 of the Taylor polynomial.
of the Taylor polynomial.
This leads to the following result:
Extreme values
Newton's method
The first Taylor polynomial  is the same as
the linearization of
is the same as
the linearization of  at the point
at the point  . This can be used
in some simple approximations and numerical methods.
. This can be used
in some simple approximations and numerical methods.
Newton's method
The equation  can be solved approximately by
choosing a starting point
can be solved approximately by
choosing a starting point  (e.g. by looking at the graph) and defining
(e.g. by looking at the graph) and defining
 for
for  This leads to a sequence
This leads to a sequence  ,
whose terms usually give better and better approximations for a zero of
,
whose terms usually give better and better approximations for a zero of  .
.
The recursion formula is based on the geometric idea of finding an
approximative zero of  by using its linearization (i.e. the tangent line).
by using its linearization (i.e. the tangent line).
Example
Find an approximate value of  by using Newton's method.
by using Newton's method.
We use Newton's method for the function  and initial value
and initial value  .
The recursion formula becomes
.
The recursion formula becomes
 from which we obtain
from which we obtain  ,
,  ,
,  and so on.
and so on.
By experimenting with these values, we find that the number of correct
decimal places doubles at each step, and  gives already 100 correct
decimal places, if intermediate steps are calculated with enough precision.
gives already 100 correct
decimal places, if intermediate steps are calculated with enough precision.
Taylor series
Taylor series
If the error term  in Taylor's Formula goes to zero as
in Taylor's Formula goes to zero as  increases,
then the limit of the Taylor polynomial
is the Taylor series of
increases,
then the limit of the Taylor polynomial
is the Taylor series of  (= Maclaurin series for
(= Maclaurin series for  ).
).
The Taylor series of  is of the form
is of the form
 This is an example of a power series.
This is an example of a power series.
The Taylor series can be formed as soon as  has derivatives of all
orders at
has derivatives of all
orders at  and they are substituted into this formula.
There are two problems related to this: Does the Taylor series converge for all values of
and they are substituted into this formula.
There are two problems related to this: Does the Taylor series converge for all values of  ?
?
Answer: Not always; for example, the function
 has a Maclaurin series (= geometric series)
converging only for
has a Maclaurin series (= geometric series)
converging only for  , although the function is differentiable for all
, although the function is differentiable for all
 :
:

If the series converges for some  , then does its sum
equal
, then does its sum
equal  ? Answer: Not always; for example, the function
? Answer: Not always; for example, the function
 satisfies
satisfies  for all
for all  (elementary but
difficult calculation). Thus its
Maclaurin series is identically zero and converges to
(elementary but
difficult calculation). Thus its
Maclaurin series is identically zero and converges to
 only at
only at  .
.
Conclusion: Taylor series should be studied carefully using the error terms. In practice, the series are formed by using some well known basic series.
Examples
\begin{align}
\frac{1}{1-x} &= \sum_{k=0}^{\infty} x^k,\ \ |x|< 1 \\
e^x &= \sum_{k=0}^{\infty} \frac{1}{k!}x^k, \ \ x\in \mathbb{R} \\
\sin x &= \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k+1)!} x^{2k+1}, \ \ x\in \mathbb{R} \\
\cos x &= \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k)!} x^{2k},\ \ x\in \mathbb{R} \\
(1+x)^r &= 1+\sum_{k=1}^{\infty} \frac{r(r-1)(r-2)\dots (r-k+1)}{k!}x^k,
|x|<1
\end{align}
The last is called the Binomial Series and is valid for all  . If
. If
 , then starting from
, then starting from
 , all the coefficients are zero and in the beginning
, all the coefficients are zero and in the beginning

Compare this to the Binomial Theorem:
 for
for  .
.
Power series
Definition: Power series
A power series is of the form
 The point
The point  is the centre and the
is the centre and the  are the coefficients of the
series.
are the coefficients of the
series.
There are only three essentially different cases:
Abel's Theorem.
- The power series converges only for
 (and then it consists of
the constant
(and then it consists of
the constant  only)
only) - The power series converges for all

- The power series converges on some interval
![]x_0-R,x_0+R[ ]x_0-R,x_0+R[](https://mycourses.aalto.fi/filter/tex/pix.php/2fd864d834cac73e2a4d36123a80ee3e.gif) (and possibly
in one or both of the end points), and diverges for other values of
(and possibly
in one or both of the end points), and diverges for other values of  .
.
The number  is the radius of convergence of the series. In the first two cases we say that
is the radius of convergence of the series. In the first two cases we say that  or
or  respectively.
respectively.
Example
For which values of the variable  does the power series
does the power series
 converge?
converge?
We use the ratio test with  . Then
. Then
 as
as  . By the ratio test, the series converges for
. By the ratio test, the series converges for  ,
and diverges for
,
and diverges for  . In the border-line cases
. In the border-line cases
 the general term of the series
does not tend to zero, so the series diverges.
the general term of the series
does not tend to zero, so the series diverges.
Result: The series converges for  , and diverges otherwise.
, and diverges otherwise.
Definition: Sum function
In the interval  where the series converges, we can
define a function
where the series converges, we can
define a function  by setting
\begin{equation}
\label{summafunktio}
f(x) = \sum_{k=0}^{\infty} c_k(x-x_0)^k, \tag{1}
\end{equation}
which is called the sum function of the power series.
by setting
\begin{equation}
\label{summafunktio}
f(x) = \sum_{k=0}^{\infty} c_k(x-x_0)^k, \tag{1}
\end{equation}
which is called the sum function of the power series.
The sum function  is continuous and differentiable on
is continuous and differentiable on ![]x_0-R,x_0+R[ ]x_0-R,x_0+R[](https://mycourses.aalto.fi/filter/tex/pix.php/2fd864d834cac73e2a4d36123a80ee3e.gif) .
Moreover, the derivative
.
Moreover, the derivative  can be calculated by differentiating the sum function
term by term:
can be calculated by differentiating the sum function
term by term:
 Note. The constant term
Note. The constant term  disappears and the series starts with
disappears and the series starts with  .
The differentiated series converges in the same interval
.
The differentiated series converges in the same interval
![x\in \, ]x_0-R,x_0+R[ x\in \, ]x_0-R,x_0+R[](https://mycourses.aalto.fi/filter/tex/pix.php/d78ea0cb1a77dcbd15ccf984e92e4a20.gif) ; this may sound a bit surprising because of the
extra coefficient
; this may sound a bit surprising because of the
extra coefficient  .
.
Example
Find the sum function of the power series 
This series is obtained by differentiating termwise the geometric series
(with  ). Therefore,
\begin{align}
1+2x+3x^2+4x^3+\dots &= D(1+x+x^2+x^3+x^4+\dots ) \\
&= \frac{d}{dx}\left( \frac{1}{1-x}\right) = \frac{1}{(1-x)^2}.
\end{align}
Multiplying with
). Therefore,
\begin{align}
1+2x+3x^2+4x^3+\dots &= D(1+x+x^2+x^3+x^4+\dots ) \\
&= \frac{d}{dx}\left( \frac{1}{1-x}\right) = \frac{1}{(1-x)^2}.
\end{align}
Multiplying with  we obtain
we obtain
 which is valid for
which is valid for  .
.
In the case ![[a,b]\subset\ ]x_0-R,x_0+R[ [a,b]\subset\ ]x_0-R,x_0+R[](https://mycourses.aalto.fi/filter/tex/pix.php/8d3ffcad3d0765d5d2a862f2664432be.gif) we can also integrate the sum function
termwise:
we can also integrate the sum function
termwise:
 Often the definite integral can be extended up to the end points of the
interval of convergence, but this is not always the case.
Often the definite integral can be extended up to the end points of the
interval of convergence, but this is not always the case.
Example
Calculate the sum of the alternating harmonic series.
Let us first substitute  to the geometric series. This yields
to the geometric series. This yields
 By integrating both sides from
By integrating both sides from  to
to  we obtain
we obtain
 Note. Extending the limit of integration all the way up to
Note. Extending the limit of integration all the way up to  should be justified
more rigorously here. We shall return to integration later on the course.
should be justified
more rigorously here. We shall return to integration later on the course.
 ',
label : { useMathJax : true }
});
board.update();
i++;
}
function reset(){
i = 0;
document.getElementById("x0").disabled = false;
document.getElementById("x0").value = "";
board.removeObject(points), board.removeObject(segments),
board.removeObject(tangents);
points = [], segments = [], tangents = [];
board.fullUpdate();
}
document.getElementById("iterate").onclick = iterate;
document.getElementById("reset").onclick = reset;
board.fullUpdate();
})();
',
label : { useMathJax : true }
});
board.update();
i++;
}
function reset(){
i = 0;
document.getElementById("x0").disabled = false;
document.getElementById("x0").value = "";
board.removeObject(points), board.removeObject(segments),
board.removeObject(tangents);
points = [], segments = [], tangents = [];
board.fullUpdate();
}
document.getElementById("iterate").onclick = iterate;
document.getElementById("reset").onclick = reset;
board.fullUpdate();
})();
6. Elementary functions
This chapter gives some background to the concept of a function. We also consider some elementary functions from a (possibly) new viewpoint. Many of these should already be familiar from high school mathematics, so in some cases we just list the main properties.
Functions
Definition: Function
A function  is a rule that
determines for each element
is a rule that
determines for each element  exactly one element
exactly one element  .
We write
.
We write  .
.
Definition: Domain and codomain
In the above definition of a function  is the domain (of definition) of the function
is the domain (of definition) of the function  and
and  is called the codomain
of
is called the codomain
of  .
.
Definition: Image of a function
The image of  is the subset
is the subset
![f[A]= \{ f(a) \mid a\in A\} f[A]= \{ f(a) \mid a\in A\}](https://mycourses.aalto.fi/filter/tex/pix.php/c7a396190ef1775b42655b3bae2aeea4.gif) of
of  . An alternative name for image is range.
. An alternative name for image is range.
For example,  ,
,  , has codomain
, has codomain  ,
but its image is
,
but its image is ![f[\mathbb{R} ] =[0,\infty[ f[\mathbb{R} ] =[0,\infty[](https://mycourses.aalto.fi/filter/tex/pix.php/0c14bcce17985fbb3a35d6def4a9a469.gif) .
.
The function in the previous example can also be defined as
 ,
,  , and then the codomain is the same as the image.
In principle, this modification can always be done, but it is not reasonable
in practice.
, and then the codomain is the same as the image.
In principle, this modification can always be done, but it is not reasonable
in practice.
Inverse functions
Observe: A function becomes surjective if all redundant points of the codomain are left out. A function becomes injective if the domain is reduced so that no value of the function is obtained more than once.
Another way of defining these concepts is based on the number of solutions to an equation:
Definition
Definition: Inverse function
If  is bijective, then it has an inverse
is bijective, then it has an inverse
 , which is uniquely determined by the condition
, which is uniquely determined by the condition

The inverse satisfies  for all
for all  and
and
 for all
for all  .
.
The graph of the inverse is the mirror image of the graph of  with respect to the
line
with respect to the
line  : A point
: A point  lies on the graph of
lies on the graph of 




 the point
the point  lies on the
graph of
lies on the
graph of  . The geometric interpretation of
. The geometric interpretation of  is precisely the
reflection with respect to
is precisely the
reflection with respect to  .
.
If  and
and  is strictly monotone, then
the function
is strictly monotone, then
the function ![f\colon A \to f[A] f\colon A \to f[A]](https://mycourses.aalto.fi/filter/tex/pix.php/c6fc43e8a306502af369ccf4e67dfa13.gif) has an inverse.
has an inverse.
If here  is an interval and
is an interval and  is continuous, then also
is continuous, then also  is
is continuous in the set
is
is continuous in the set ![f[A] f[A]](https://mycourses.aalto.fi/filter/tex/pix.php/e81e3f1f3f2f27271e7259b5b1e92b05.gif) .
.
Theorem: Derivative of the inverse
Let ![f\colon \, ]a,b[\, \to\, ]c,d[ f\colon \, ]a,b[\, \to\, ]c,d[](https://mycourses.aalto.fi/filter/tex/pix.php/d743062611593c099de64ea09a96ce0e.gif) be differentiable and bijective, so that it has an inverse
be differentiable and bijective, so that it has an inverse
![f^{-1}\colon \, ]c,d[\, \to\, ]a,b[ f^{-1}\colon \, ]c,d[\, \to\, ]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/12920db7181cead890f182a6b37094a0.gif) . As the graphs
. As the graphs  and
and  are mirror images of each other, it seems geometrically obvious that also
are mirror images of each other, it seems geometrically obvious that also  is differentiable, and we actually have
is differentiable, and we actually have
 if
if  .
.
Transcendental functions
Trigonometric functions
Unit of measurement of an angle = rad: the arclength of the arc on the unit circle, that corresponds to the angle.
The functions
 are defined in terms of the unit circle so that
are defined in terms of the unit circle so that
 ,
, ![x\in [0,2\pi] x\in [0,2\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/45279ec769d88b24314782eea30c7f1e.gif) , is the point on the unit circle corresponding to the
angle
, is the point on the unit circle corresponding to the
angle  , measured counterclockwise from the point
, measured counterclockwise from the point  .
.


Proof: Pythagorean Theorem.
Addition formulas:
Basic properties (from the unit circle!)
Proof: Geometrically, or more easily with vectors and matrices.
Example
It follows that the functions
 and
and  satisfy the
differential equation
satisfy the
differential equation
 that models harmonic oscillation. Here
that models harmonic oscillation. Here  is the time variable
and the constant
is the time variable
and the constant  is the angular frequency of the oscillation.
We will see later that all the solutions of this differential equation
are of the form
is the angular frequency of the oscillation.
We will see later that all the solutions of this differential equation
are of the form
 with
with  constants. They will be uniquely determined if we know
the initial location
constants. They will be uniquely determined if we know
the initial location  and the initial velocity
and the initial velocity  . All solutions
are periodic and their period is
. All solutions
are periodic and their period is  .
.
Arcus functions
The trigonometric functions have inverses if their domain and codomains are chosen in a suitable way.
Here we will only prove the first result (1). By differentiating
both sides of the equation  for
for  :
:



The last row follows also directly from the formula for the derivative of an inverse.
Example
Example
Derive the addition formula for tan, and show that

Solutions: Voluntary exercises. The first can be deduced by looking at
a rectangular triangle with the length of the hypotenuse equal to 1
and one leg of length  .
.
Introduction: Radioactive decay
Let  model the number of radioactive nuclei at time
model the number of radioactive nuclei at time  .
During a short time interval
.
During a short time interval  the number of decaying nuclei is (approximately) directly proportional to
the length of the interval, and also to the number of nuclei at time
the number of decaying nuclei is (approximately) directly proportional to
the length of the interval, and also to the number of nuclei at time  :
:
 The constant
The constant  depends on the substance and is called the decay constant.
From this we obtain
depends on the substance and is called the decay constant.
From this we obtain
 and in the limit as
and in the limit as  we end up with the differential equation
we end up with the differential equation  .
.
Exponential function
Definition: Exponential function
The Exponential function exp:
 This definition (using the series expansion) is based on the conditions
This definition (using the series expansion) is based on the conditions
 and
and  , which imply
that
, which imply
that  for all
for all  ,
so the Maclaurin series is the one above.
,
so the Maclaurin series is the one above.
The connections between different expressions are surprisingly tedious to prove, and we omit the details here. The main steps include the following:
From here on we write  . Properties:
. Properties:
 .
.
Differential equation 
Theorem
Let  be a constant. All solutions
be a constant. All solutions  of the ordinary differenial equation (ODE)
of the ordinary differenial equation (ODE)
 are of the form
are of the form  , where
, where  is a constant. If we know
the value of
is a constant. If we know
the value of  at some point
at some point  , then the constant
, then the constant
 will be uniquely determined.
will be uniquely determined.
Euler's formula
Definition: Complex numbers
Imaginary unit  : a strange creature satisfying
: a strange creature satisfying  . The complex numbers
are of the form
. The complex numbers
are of the form  , where
, where  . We will return to these later.
. We will return to these later.
Theorem: Euler's formula
If we substitute  as a variable in the expontential fuction, and
collect real terms separately, we obtain Euler's formula
as a variable in the expontential fuction, and
collect real terms separately, we obtain Euler's formula

 in the definition of the exponential function and write the series as the sum
of its even (
in the definition of the exponential function and write the series as the sum
of its even ( ) and odd
) and odd  parts. Note that
parts. Note that  and remember the Taylor series of the trigonometric
functions.
and remember the Taylor series of the trigonometric
functions.
As a special case we have Euler's identity  .
It connects the most important numbers
.
It connects the most important numbers  ,
,  ,
,  ,
,  ja
ja  and the
three basic operations sum, multiplication, and power.
and the
three basic operations sum, multiplication, and power.
Logarithms
Hyperbolic functions
Definition: Hyperbolic functions
Hyperbolic sine sinus hyperbolicus  ,
hyperbolic cosine cosinus hyperbolicus
,
hyperbolic cosine cosinus hyperbolicus  and hyperbolic tangent
and hyperbolic tangent
 are defined as
are defined as


![\tanh \colon \mathbb{R}\to \ ]-1,1[, \ \tanh x =\frac{\sinh x}{\cosh x} \tanh \colon \mathbb{R}\to \ ]-1,1[, \ \tanh x =\frac{\sinh x}{\cosh x}](https://mycourses.aalto.fi/filter/tex/pix.php/2ac4198587d98a4f7dd3df05218f66f7.gif)
Properties:  ; all trigonometric have their hyperbolic counterparts,
which follow from the properties
; all trigonometric have their hyperbolic counterparts,
which follow from the properties  ,
,  .
In these formulas, the sign of
.
In these formulas, the sign of  will change, but the other signs remain the same.
will change, but the other signs remain the same.
Hyperbolic inverse functions: the so-called area functions;
area and the shortening ar refer to a certain geometrical area
related to the hyperbola  :
:


 ',
radius : .4,
label : { useMathJax : true, strokeColor : 'black', offset : [0, .5] }
});
var info = board.create('text', [-1.2, -1.25, function() {
return '
',
radius : .4,
label : { useMathJax : true, strokeColor : 'black', offset : [0, .5] }
});
var info = board.create('text', [-1.2, -1.25, function() {
return ' ';
}], {
useMathJax : true,
fixed : true
});
board.fullUpdate();
})();
';
}], {
useMathJax : true,
fixed : true
});
board.fullUpdate();
})();
7. Area
Table of Content
Area in the plane
We consider areas of plane sets bounded by closed curves. In the more general cases, the concept of area becomes theoretically very difficult.
The area of a planar set is defined by reducing to the areas of simpler sets. The area cannot be "calculated", unless we first have a definition of "area" (although this is common practice in school mathematics).
Starting point
Polygon
A (simple) polygon is a plane set bounded by a closed curve that consists of a finite number of line segments without self-intersections.
Definition: Area of a polygon
The area of a polygon is defined by dividing it into a
finite number of triangles (called a
Theorem.
The sum of the areas of triangles in a triangulation of a polygon is the same for all triangulations.
General case
 has an area if for every
has an area if for every  there is an inner polygon
there is an inner polygon  and an outer polygon
and an outer polygon  , whose areas differ by less
than
, whose areas differ by less
than  :
:
 This implies that between all areas
This implies that between all areas  and
and  there is a unique real number
there is a unique real number  ,
which is (by definition) the area of
,
which is (by definition) the area of  .
.
A surprise: The condition that  is bounded by a closed curve (without self-intersections)
does not guarantee that it has an area! Reason: The boundary curve can be so "wiggly",
that it has positive "area". The first such example was constucted by [W.F. Osgood, 1903]:
is bounded by a closed curve (without self-intersections)
does not guarantee that it has an area! Reason: The boundary curve can be so "wiggly",
that it has positive "area". The first such example was constucted by [W.F. Osgood, 1903]:
8. Integral
From sum to integral
Definite integral
Geometric interpretation: Let ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) be such that
be such that  for all
for all
![x\in[a,b] x\in[a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/c7c42309c359c25dfe77f397d5261997.gif) . How can we find the area of the region bounded by the function graph
. How can we find the area of the region bounded by the function graph  , the
x-axis and the two lines
, the
x-axis and the two lines  and
and  ?
?
The answer to this question is given by the definite integral
 Remark. The general definition of the integral does not necessitate the condition
Remark. The general definition of the integral does not necessitate the condition  .
.
Integration of continuous functions
Definition: Partition
Let ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) be continuous. A finite sequence
be continuous. A finite sequence  of real numbers such that
of real numbers such that
 is called a partition of the interval
is called a partition of the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) .
.
Definition: Upper and lower sum
For each partition  we define the related upper sum of the function
we define the related upper sum of the function  as
as
 and the lower sum as
and the lower sum as

If  is a positive function then the upper sum represents the total area of the rectangles circumscribing
the function graph and similarly the lower sum is the total area of the inscribed rectangles.
is a positive function then the upper sum represents the total area of the rectangles circumscribing
the function graph and similarly the lower sum is the total area of the inscribed rectangles.
Properties of partitions
Definition: Integrability
We say that a function ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) is integrable if for every
is integrable if for every  there exists a corresponding partition
there exists a corresponding partition  of
of ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) such that
such that

Definition: Integral
Integrability implies that there exists a unique real number  such that
such that  for every
partition
for every
partition  . This is called the integral of
. This is called the integral of  over the interval
over the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) and denoted by
and denoted by

Remark. This definition of the integral is sometimes referred to as the Darboux integral.
For non-negative functions  this definition of the integral coincides with the idea of making the difference
between the the areas of the circumscribed and the inscribed rectangles arbitrarily small by using ever finer partitions.
this definition of the integral coincides with the idea of making the difference
between the the areas of the circumscribed and the inscribed rectangles arbitrarily small by using ever finer partitions.
Theorem.
A continuous function on a closed interval is integrable.
Here we will only provide the proof for continuous functions with bounded derivatives.
Suppose that ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) is a continuous function and that there exists a constant
is a continuous function and that there exists a constant  such that
such that
 for all
for all ![x\in]a,b[ x\in]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/446e008dffdc84c23608a41270477f2f.gif) . Let
. Let  and define
and define  to be an equally spaced partition of
to be an equally spaced partition of ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) such that
such that
 Let
Let  and
and  for some suitable points
for some suitable points ![y_{k},z_{k}\in[x_{k-1},x_{k}] y_{k},z_{k}\in[x_{k-1},x_{k}]](https://mycourses.aalto.fi/filter/tex/pix.php/b0cc09fba8e4e83e7252a84f0c0d25e5.gif) . The mean value theorem
then states that
. The mean value theorem
then states that
 and thus
and thus

Definition: Riemann integral
Suppose that ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) is a continuous function and let
is a continuous function and let
 be a partition of
be a partition of ![\left[a,b\right] \left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/22be842f9527b4b0ef3b7085b5486b7b.gif) and
and
 be a sequence of real numbers such that
be a sequence of real numbers such that
![z_{k}\in[x_{k-1},x_{k}] z_{k}\in[x_{k-1},x_{k}]](https://mycourses.aalto.fi/filter/tex/pix.php/6699d41c4ee1c2de849bc6a2162fd4e7.gif) for all
for all  . The partial sums
. The partial sums
 are called the Riemann sums of
are called the Riemann sums of  . Suppose further that the partitions are
such that
. Suppose further that the partitions are
such that  as
as  .
The integral of
.
The integral of  can then be defined as the limit
can then be defined as the limit
 This definition of the integral is called the Riemann integral.
This definition of the integral is called the Riemann integral.
Remark. This definition of the integral turns out to be equivalent to that of the Darboux integral i.e. a function is Riemann-integrable if and only if it is Darboux-integrable and the values of the two integrals are always equal.
Example
Find the integral of  over the interval
over the interval ![[0,1] [0,1]](https://mycourses.aalto.fi/filter/tex/pix.php/ccfcd347d0bf65dc77afe01a3306a96b.gif) using Riemann sums.
using Riemann sums.
Let  . Then
. Then  ,
,  and
and  for all
for all
 . Thus the sequence
. Thus the sequence  is a proper
partition of
is a proper
partition of ![\left[0,1\right] \left[0,1\right]](https://mycourses.aalto.fi/filter/tex/pix.php/4f27db35c23e1b587a92f6ba055a4b94.gif) . This partition has the pleasant property hat
. This partition has the pleasant property hat
 is a constant. Estimating the Riemann sums we now find that
is a constant. Estimating the Riemann sums we now find that

 as
as  and hence
and hence

This is of course the area of the triangular region bounded by the line  ,
the
,
the  -axis and the lines
-axis and the lines  and
and  .
.
Remark. Any interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) can be partitioned into equally spaced subintervals by setting
can be partitioned into equally spaced subintervals by setting
 and
and  .
.
Conventions
Piecewise-defined functions
Definition: Piecewise continuity
A function ![f\colon\left[a,b\right]\to\mathbb{R} f\colon\left[a,b\right]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/651a926e83a81b2331659e5bec837922.gif) is called piecewise continuous
if it is continuous except at a finite number of points
is called piecewise continuous
if it is continuous except at a finite number of points
 and the one-sided limits of the function are defined and bounded on each of these
points. It follows that the restriction of
and the one-sided limits of the function are defined and bounded on each of these
points. It follows that the restriction of  on each subinterval
on each subinterval
![\left[c_{k-1},c_{k}\right] \left[c_{k-1},c_{k}\right]](https://mycourses.aalto.fi/filter/tex/pix.php/4c8251634c3e4dcef42dea1404161757.gif) is continuous if the one-sided limits are taken to
be the values of the function at the end points of the subinterval.
is continuous if the one-sided limits are taken to
be the values of the function at the end points of the subinterval.
Definition: Piecewise integration
Let ![f\colon\left[a,b\right] f\colon\left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/9f37a3c940314dccb310e7db856fb524.gif) be a piecewise continuous function. Then
be a piecewise continuous function. Then
 where
where  and
and  is thought as a
continuous function on each subinterval
is thought as a
continuous function on each subinterval ![\left[c_{k-1},c_{k}\right] \left[c_{k-1},c_{k}\right]](https://mycourses.aalto.fi/filter/tex/pix.php/4c8251634c3e4dcef42dea1404161757.gif) . Usually
functions which are continuous yet piecewise defined are also integrated using the
same idea.
. Usually
functions which are continuous yet piecewise defined are also integrated using the
same idea.
Important properties
Properties
Suppose that ![f,g\colon\left[a,b\right]\to\mathbb{R} f,g\colon\left[a,b\right]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/f01d397fa4a741a5373783b544f03897.gif) are piecewise continuous
functions. The integral has the following properties
are piecewise continuous
functions. The integral has the following properties
Fundamental theorem of calculus
Theorem: Mean value theorem
Let ![f\colon[a,b]\to\mathbb{R} f\colon[a,b]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/4bbb5ba4231dc6733dfafd89107596a5.gif) be a continuous function. Then there exists
be a continuous function. Then there exists  such that
such that
 This is the mean value of
This is the mean value of  on the interval
on the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) and we denote it with
and we denote it with  .
.
Antiderivative
If  on some open interval then
on some open interval then  is the antiderivative
(or the primitive function) of
is the antiderivative
(or the primitive function) of  . The fundamental theorem of calculus
guarantees that for every continuous function
. The fundamental theorem of calculus
guarantees that for every continuous function  there exists an antiderivative
there exists an antiderivative
 The antiderivative is not necessarily expressible as a combination of elementary
functions even if
The antiderivative is not necessarily expressible as a combination of elementary
functions even if  were an elementary function, e.g.
were an elementary function, e.g.  .
Such primitives are called nonelementary antiderivatives.
.
Such primitives are called nonelementary antiderivatives.
Suppose that  for all
for all  . Then the derivative of
. Then the derivative of  is identically zero and thus the difference is a constant.
is identically zero and thus the difference is a constant.
(Second) Fundamental theorem of calculus
Let ![f\colon\left[a,b\right]\to\mathbb{R} f\colon\left[a,b\right]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/651a926e83a81b2331659e5bec837922.gif) be a continuous function and
be a continuous function and  an antiderivative of
an antiderivative of  , then
, then

Integrals of elementary functions
Constant Functions
Given the constant function  . The integral
. The integral  has to be determined now.
has to be determined now.
Solution by finding a antiderivative
From the previous chapter it is known that  gives
gives  . This means that
. This means that  is an antiderivative for
is an antiderivative for  . So the following applies
. So the following applies ![\int\limits_a^b c \, \mathrm{d}x = [c \cdot x]_{x=a}^{x=b} = c\cdot b - c \cdot a = c \cdot (b-a). \int\limits_a^b c \, \mathrm{d}x = [c \cdot x]_{x=a}^{x=b} = c\cdot b - c \cdot a = c \cdot (b-a).](https://mycourses.aalto.fi/filter/tex/pix.php/8665eaa9c4f246caaa2ed563cb0a03e8.gif)
Remark: Of course, a function  would also be an antiderivative of
would also be an antiderivative of  , since the constant
, since the constant  is omitted in the derivation. For sake of simplicity
is omitted in the derivation. For sake of simplicity  can be used, since
can be used, since  can be chosen as
can be chosen as  for definite integrals.
for definite integrals.
Solution by geometry
The area under the constant function forms a rectangle with height  and length
and length  . Thus the area is
. Thus the area is  and this corresponds to the solution of the integral. Illustrate this remark by a sketch.
and this corresponds to the solution of the integral. Illustrate this remark by a sketch.
Linear functions
Given is the linear function  . We are looking for the integral
. We are looking for the integral  .
.
Solve by finding a antiderivative
The antiderivative of a linear function is in any case a quadratic function, since  . The derivative of a quadratic function results in a linear function. Here, it is important to consider the leading factor as in
. The derivative of a quadratic function results in a linear function. Here, it is important to consider the leading factor as in  Thus the result is
Thus the result is ![\int\limits_a^b mx \mathrm{d}x = \left[\frac{m}{2}x^2 \right]_{x=a}^{x=b}= \frac{m}{2}b^2 - \frac{m}{2}a^2. \int\limits_a^b mx \mathrm{d}x = \left[\frac{m}{2}x^2 \right]_{x=a}^{x=b}= \frac{m}{2}b^2 - \frac{m}{2}a^2.](https://mycourses.aalto.fi/filter/tex/pix.php/b5241a45e0cf510936549697bfb8ec04.gif)
Solving by geometry
The integral  can be seen geometrically, as subtracting the triangle with the edges
can be seen geometrically, as subtracting the triangle with the edges  ,
,  and
and  from the triangle with the edges
from the triangle with the edges  ,
,  and
and  . Since the area of a triangle ist given by
. Since the area of a triangle ist given by  , the area of the first triangle
, the area of the first triangle  and that of the second triangle is analogous
and that of the second triangle is analogous  . For the integral the result is
. For the integral the result is  . This is consistent with the integral calculated using the antiderivative. Illustrate this remark by a sketch.
. This is consistent with the integral calculated using the antiderivative. Illustrate this remark by a sketch.
Power functions
In constant and linear functions we have already seen that the exponent of a function decreases by one when it is derived. So it has to get bigger when integrating.
The following applies:  It follows that the antiderivative for
It follows that the antiderivative for  must have the exponent
must have the exponent  ,
,  By multiplying the last equation with
By multiplying the last equation with  we get
we get  Finally the antiderivative is
Finally the antiderivative is  .
.
Examples
The formula ![\int x^n\, \mathrm dx = [\frac{1}{n+1} x^{n+1}] \int x^n\, \mathrm dx = [\frac{1}{n+1} x^{n+1}]](https://mycourses.aalto.fi/filter/tex/pix.php/222a5eca783899397010e410d9be1ac6.gif) is also valid, if the exponent of the function is a real number and not equal
is also valid, if the exponent of the function is a real number and not equal  .
.
Examples
Natural Exponential function
The natural exponential function  is one of the easiest function to differentiate and integrate.
Since the derivation of
is one of the easiest function to differentiate and integrate.
Since the derivation of  results in
results in  , it follows
, it follows 
Example 1
Determine the value of the integral  .
.
Example 2
Determine the value of the integral  . Using the same considerations as above we get
. Using the same considerations as above we get  Important is here, that we have to use the factor
Important is here, that we have to use the factor  .
.
Natural Logarithm
The derivative of the natural logarithmic function is  for
for  . It even applies
. It even applies  to
to  . These results together result in for the antiderivative of
. These results together result in for the antiderivative of 

An antiderivative can be specified for the natural logarithm: 
Trigonometric function
The antiderivatives of  and
and  also result logically if you derive "backwards". We have
also result logically if you derive "backwards". We have
 since
since  Furthermore we know
Furthermore we know  since
since  applies.
applies.
Example 1
Which area is covered by the sine on the interval ![[0,\pi] [0,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/a79560c6f70853be01bb23f7539e168c.gif) and the
and the  -axis?
To determination the area we simply have to evaluate the integral
-axis?
To determination the area we simply have to evaluate the integral
 That means
That means ![\int_0^{\pi} \sin(\tau) \, \mathrm{d}\tau = \left[-\cos(\tau)\right]_{\tau=0}^{\tau=\pi} =
-\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 2. \int_0^{\pi} \sin(\tau) \, \mathrm{d}\tau = \left[-\cos(\tau)\right]_{\tau=0}^{\tau=\pi} =
-\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 2.](https://mycourses.aalto.fi/filter/tex/pix.php/ed010b1da078996da59e937f6091bf5f.gif) Again make a sketch for this example.
Again make a sketch for this example.
Example 2
How can the integral  be expressed analytically?
be expressed analytically?
To determine the integral we use the antiderivative of the cosine:  . However, the inner derivativ has to be considered in the
given function and thus we get
. However, the inner derivativ has to be considered in the
given function and thus we get 
Example 1
Solution. The antiderivative of  is
is  so we have that
so we have that
 The antiderivative of
The antiderivative of  is
is  and thus
and thus

Example 2
Solution. The antiderivative might look something like  , where we can find the factor
, where we can find the factor  through differentiation:
through differentiation:
 hence if
hence if  we get the correct antiderivative. Thus
we get the correct antiderivative. Thus
 This integral can also be solved using integration by substitution; more on this method later.
This integral can also be solved using integration by substitution; more on this method later.
Geometric applications
Area of a plane region
Suppose that  and
and  are piecewise continuous functions. The area of a region bounded by the graphs
are piecewise continuous functions. The area of a region bounded by the graphs  ,
,  and the vertical lines
and the vertical lines  and
and  is given by the integral
is given by the integral

Especially if  is a non-negative function on the interval
is a non-negative function on the interval ![[a,b] [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) and
and  for all
for all  then the integral
then the integral
 is the area of the region bounded by the graph
is the area of the region bounded by the graph  , the
, the  -axis and the vertical lines
-axis and the vertical lines  and
and  .
.
Arc length
Surface of revolution
The area of a surface generated by rotating the graph  around the
around the  -axis on the interval
-axis on the interval ![\left[a,b\right] \left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/22be842f9527b4b0ef3b7085b5486b7b.gif) is given by
is given by
 Heuristic reasoning: An area element of the surface is approximately
Heuristic reasoning: An area element of the surface is approximately

Solid of revolution
Suppose that the cross-sectional area of a solid is given by the function  when
when ![x\in\left[a,b\right] x\in\left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/2f48f5b87131a8927f62cdab351ef9f5.gif) . Then the volume of the solid is given by the integral
. Then the volume of the solid is given by the integral
 If the graph
If the graph  is rotated around the
is rotated around the  -axis between the lines
-axis between the lines  and
and  the volume of the generated figure (the solid of revolution) is
the volume of the generated figure (the solid of revolution) is
 This follows from the fact that the cross-sectional area of the figure at
This follows from the fact that the cross-sectional area of the figure at  is a circle with radius
is a circle with radius  i.e.
i.e.  .
.
More generally: Let  and suppose that the region bounded by
and suppose that the region bounded by  and
and  and the lines
and the lines  and
and  is rotated around the
is rotated around the  -axis. The volume of this solid of revolution is
-axis. The volume of this solid of revolution is

Improper integral
Definition: Improper integral
One limitation of the improper integration is that the limit must be taken with respect to one endpoint at a time.
Example
 Provided that both of the integrals on the right-hand side converge. If either of the two is divergent then so is the integral.
Provided that both of the integrals on the right-hand side converge. If either of the two is divergent then so is the integral.
Definition
Let  be a piecewise continuous function. Then
be a piecewise continuous function. Then
 provided that the limit exists and is finite. We say that the improper integral of
provided that the limit exists and is finite. We say that the improper integral of  converges over
converges over  .
.
Likewise for ![f\colon\left]-\infty,b\right]\to\mathbb{R} f\colon\left]-\infty,b\right]\to\mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/cc67a3edd5c24ca829bb065e2a3d65b4.gif) we define
we define
 provided that the limit exists and is finite.
provided that the limit exists and is finite.
Example
Solution. Notice that
 as
as  . Thus the improper integral converges and
. Thus the improper integral converges and

Definition
Let  be a piecewise continuous function. Then
be a piecewise continuous function. Then
 if both of the two integrals on the right-hand side converge.
if both of the two integrals on the right-hand side converge.
However, this doesn't apply in general. For example, let  . Note that even though
. Note that even though
 for all
for all  the improper integral
the improper integral
 does not converge.
does not converge.
Improper integrals of the 2nd kind are handled in a similar way using limits. As there are many different (but essentially rather similar) cases, we leave the matter to one example only.
Comparison test
Example 2
Notice that
 and that the integral
and that the integral
 converges. Thus by the comparison test the integral
converges. Thus by the comparison test the integral
 also converges and its value is less than or equal to
also converges and its value is less than or equal to  .
.
Example 3
Likewise
 and because
and because  converges so does
converges so does
 and its value is less than or equal to
and its value is less than or equal to  .
.
Note. The choice of the dominating function depends on both the original function and the interval of integration.
Example 4
Determine whether the integral
 converges or diverges.
converges or diverges.
Solution. Notice that  for all
for all  and therefore
and therefore
 Now, because the integral
Now, because the integral  diverges then by the comparison test so does the original integral.
diverges then by the comparison test so does the original integral.
Integration techniques
Logarithmic integration
Given a quotient of differentiable functions, we know to apply the quotient rule. However, this is not so easy with integration. Here only for a few special cases we will state rules in this chapter.
Logarithmic integration As we already know the derivative of  , i.e. the natural logarithm to the base
, i.e. the natural logarithm to the base  , equal to
, equal to  . According to the chain rule the derivative of differentiable function with positive function values is
. According to the chain rule the derivative of differentiable function with positive function values is  . This means that for a quotient of functions where the numerator is the derivative of the denominator yields the rule: \begin{equation} \int \frac{f'(x)}{f(x)}\, \mathrm{d} x= \ln \left(|f(x)|\right) +c,\,c\in\mathbb{R}.\end{equation} Using the absolute value of the function is important, since the logarithm is defined on
. This means that for a quotient of functions where the numerator is the derivative of the denominator yields the rule: \begin{equation} \int \frac{f'(x)}{f(x)}\, \mathrm{d} x= \ln \left(|f(x)|\right) +c,\,c\in\mathbb{R}.\end{equation} Using the absolute value of the function is important, since the logarithm is defined on  .
.
Examples
Integration of rational functions - partial fraction decomposition
The logarithmic integration works well in special cases of broken rational functions where the counter is a multiple of the derivation of the denominator. However, other cases can sometimes be traced back to this. This method is called partial fractional decomposition, which represents rational functions as the sum of proper rational functions.
Example 1
The function  cannot be integrated at first glance. However, the denominator
cannot be integrated at first glance. However, the denominator  can be written as
can be written as  and the function can finally reads as
and the function can finally reads as  by partial fraction decomposition. This expression can be integrated, as demonstrated now: \begin{eqnarray} \int \dfrac{1}{1-x^2} \,\mathrm dx &= & \int \dfrac{\frac{1}{2}}{1+x} + \dfrac{\frac{1}{2}}{1-x}\, \mathrm dx \\ & =& \frac{1}{2} \int \dfrac{1}{1+x}\, \mathrm dx - \frac{1}{2} \int \dfrac{-1}{1-x}\, \mathrm dx\\ & = &\frac{1}{2} \ln|1+x| +c_1 - \frac{1}{2} \ln|1-x| +c_2\\ &= &\frac{1}{2} \ln \left|\dfrac{1+x}{1-x}\right|+c,\,c\in\mathbb{R}. \end{eqnarray} This procedure is now described in more detail for some special cases.
by partial fraction decomposition. This expression can be integrated, as demonstrated now: \begin{eqnarray} \int \dfrac{1}{1-x^2} \,\mathrm dx &= & \int \dfrac{\frac{1}{2}}{1+x} + \dfrac{\frac{1}{2}}{1-x}\, \mathrm dx \\ & =& \frac{1}{2} \int \dfrac{1}{1+x}\, \mathrm dx - \frac{1}{2} \int \dfrac{-1}{1-x}\, \mathrm dx\\ & = &\frac{1}{2} \ln|1+x| +c_1 - \frac{1}{2} \ln|1-x| +c_2\\ &= &\frac{1}{2} \ln \left|\dfrac{1+x}{1-x}\right|+c,\,c\in\mathbb{R}. \end{eqnarray} This procedure is now described in more detail for some special cases.
Case 1:  with
with  . In this case,
. In this case,  has the representation
has the representation  and can be transformed to
and can be transformed to  By multiplying with
By multiplying with  it yields ot
it yields ot 
 and
and  are now obtained by the method of equating the coefficients.
are now obtained by the method of equating the coefficients.
Example 2
Determe the partial fraction decomposition of  .
.
Start with the equation  to get the parameters
to get the parameters  and
and  . Multiplication by
. Multiplication by  leads to
leads to  Now we get the system of linear equations
Now we get the system of linear equations
\begin{eqnarray}A+B & = & 2 \\ 5A - 4 B &=& 3\end{eqnarray} with the solution  and
and  . The representation with proper rational functions is
. The representation with proper rational functions is  The integral of the type
The integral of the type  is no longer mystic.
is no longer mystic.
With the help of partial fraction decomposition, this integral can now be calculated in the following manner \begin{eqnarray}\int \frac{ax+b}{(x-\lambda_1)(x-\lambda_2)}\mathrm{d} x &=& \int\frac{A}{(x-\lambda_1)}+\frac{B}{(x-\lambda_2)}\mathrm{d} x \\ &=&A\int\frac{1}{(x-\lambda_1)}\mathrm{d} x +B\int\frac{1}{(x-\lambda_2)}\mathrm{d} x \\ & = & A\ln(|x-\lambda_1|) + B\ln(|x-\lambda_2|).\end{eqnarray}
Example 3
Determine the antiderivative for  , i.e.
, i.e. 
From the above example we already know: 
Using the idea explained above immediately follow:  So is the result
So is the result 
In this case  has the representation
has the representation  and the ansatz
and the ansatz  is used.
is used.
By multiplying the equation with  we get
we get  Again equating the coefficients leads us to a system of linear equations in
Again equating the coefficients leads us to a system of linear equations in  and
and 
In this case  has the representation
has the representation  and the representation can not be simplified.
and the representation can not be simplified.
Only the special case  is now considered.
is now considered.
Integration by Parts
The derivative of a product of two continuously differentiable functions  and
and  is
is 
This leads us to the following theorem:
Theorem: Integration by Parts
Let and
and  be continuously differentiable functions on the interval
be continuously differentiable functions on the interval ![\left[a,b\right] \left[a,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/22be842f9527b4b0ef3b7085b5486b7b.gif) . Then
. Then
 Likewise for the indefinite integral it holds that
Likewise for the indefinite integral it holds that

It follows from the product rule that
 or rearranging the terms
or rearranging the terms
 Integrating both sides of the equation with respect to
Integrating both sides of the equation with respect to  and ignoring the constant of integration now yields
and ignoring the constant of integration now yields

Example
Solution. Set  and
and  . Then
. Then  and
and  and the integration by parts gives
and the integration by parts gives


Notice that had we chosen  and
and  the other way around this would have led to an even more complicated integral.
the other way around this would have led to an even more complicated integral.
Integration by Substitution
Example 1
Find the value of the integral  .
.
Solution. Making the substitution  when
when  we have
we have  . Solving the limits from the inverse formula i.e.
. Solving the limits from the inverse formula i.e.  we find that
we find that  and
and  . Hence
. Hence

Here the latter integral was solved applying integration by parts in the previous example.
Example 2
![L(f)=' + rsums[1].Value().toFixed(3) + ' L(f)=' + rsums[1].Value().toFixed(3) + '](https://mycourses.aalto.fi/filter/tex/pix.php/7cca90fbd11588571c4518f7bebf98c8.gif) '; }
],{
useMathJax : true,
fontSize : 14,
fixed : true
}));
b1.fullUpdate();
b2.fullUpdate();
};
plotButton.click();
})();
',
label : { useMathJax : true, offset : [0, 30] }
});
board.create('integral', [[0.2, 1.4], graph], { fillColor : 'blue', curveRight : { visible : false }, curveLeft : { visible : false },
withLabel : false,
baseLeft : { visible : true, showinfobox : false, size : 1, strokeColor : 'black', withLabel : true, name : '
'; }
],{
useMathJax : true,
fontSize : 14,
fixed : true
}));
b1.fullUpdate();
b2.fullUpdate();
};
plotButton.click();
})();
',
label : { useMathJax : true, offset : [0, 30] }
});
board.create('integral', [[0.2, 1.4], graph], { fillColor : 'blue', curveRight : { visible : false }, curveLeft : { visible : false },
withLabel : false,
baseLeft : { visible : true, showinfobox : false, size : 1, strokeColor : 'black', withLabel : true, name : ' ', label : { useMathJax : true, offset : [0, -1] }},
baseRight : { visible : true, showinfobox : false, size : 1, strokeColor : 'black', withLabel : true, name : '
', label : { useMathJax : true, offset : [0, -1] }},
baseRight : { visible : true, showinfobox : false, size : 1, strokeColor : 'black', withLabel : true, name : ' ', label : { useMathJax : true, offset : [0, -1] }}
} );
board.fullUpdate();
})();
', label : { useMathJax : true, offset : [0, -1] }}
} );
board.fullUpdate();
})();
9. Differential equations
Introduction
Differential equation is an equation containing an unknown function, e.g.  , and its derivatives
, and its derivatives  . This kind of equation where the unknown function depends on a single variable, is called an ordinary differential equation (ODE) or simply a differential equation. If the unknown function contains several variables, it is called partial differential equation, but they are not covered in this course.
. This kind of equation where the unknown function depends on a single variable, is called an ordinary differential equation (ODE) or simply a differential equation. If the unknown function contains several variables, it is called partial differential equation, but they are not covered in this course.
A typical application leading to a differential equation is radioactive decay. If  is the number of radioactive nuclei present at time
is the number of radioactive nuclei present at time  , then during a short time interval
, then during a short time interval  the
change in this number is approximately
the
change in this number is approximately  , where
, where  is a positive constant depending on the radioactive substance. The approximation becomes better as
is a positive constant depending on the radioactive substance. The approximation becomes better as  , so that
, so that  . It follows that the differential equation
. It follows that the differential equation  is a mathematical model for the radioactive decay. In reality, the number of nuclei is an integer, so the function
is a mathematical model for the radioactive decay. In reality, the number of nuclei is an integer, so the function  is not differentiable (or the derivative is mostly zero!). Therefore, the model describes the properties of some idealized smooth version of
is not differentiable (or the derivative is mostly zero!). Therefore, the model describes the properties of some idealized smooth version of  . This is a typical phenomenon in most models.
. This is a typical phenomenon in most models.
Order
The order of a differential equation is the highest order of the derivatives appearing in the equation.
For example, the order of the differential equation  is 1. The order of the differential equation
is 1. The order of the differential equation  is 2.
is 2.
Here the variable of the function  is not visible; the equation is considered to
determine
is not visible; the equation is considered to
determine  implicitly.
implicitly.
Solutions of a differential equation
A differential equation of order n is of the form
The solution to an ODE is an n times differentiable function  satisfying the above equation for all
satisfying the above equation for all  where
where  is an open interval in the real axis.
is an open interval in the real axis.
Typically the solution is not unique and there can be an infinite number of solutions. Consider the equation  The equation has the solutions
The equation has the solutions
Here  ,
,  and
and  are called particular solutions. The general solution is
are called particular solutions. The general solution is  Particular solutions can be derived from the general solution by assigning the parameter
Particular solutions can be derived from the general solution by assigning the parameter  to some value. Solutions that cannot be derived from the general solution are called special solutions.
to some value. Solutions that cannot be derived from the general solution are called special solutions.
Differential equations do not necessarily have any solutions at all. For example, the first order differential equation  does not have any solutions. If a first order equation can be written in normal form
does not have any solutions. If a first order equation can be written in normal form  , where
, where  is continuous, then a solution exists.
is continuous, then a solution exists.
Initial condition
Constants in the general solution can be assigned to some values if the solution is required to satisfy additional properties. We may for example demand that the solution equals  at
at  by setting an initial condition
by setting an initial condition  With first order equations, only one condition is (usually) needed to make the solution unique. With second order equations, we need two conditions, respectively. In this case, the initial condition is of the form
With first order equations, only one condition is (usually) needed to make the solution unique. With second order equations, we need two conditions, respectively. In this case, the initial condition is of the form
In general, for an equation of order n, we need n extra conditions to make the solution unique. A differential equation and its set initial conditions are jointly referred as an initial value problem.
Example 1.
We saw above that the the general solution to the differential equation  is
is  Therefore the solution to the initial value problem
Therefore the solution to the initial value problem
Interactive. In the figure above, some of the solutions to the equation
 are drawn. Try out and see how the initial condition alters the solution. The initial values can be changed by dragging the points. Is it possible to make the solution curves intersect?
are drawn. Try out and see how the initial condition alters the solution. The initial values can be changed by dragging the points. Is it possible to make the solution curves intersect?
Direction field
The differential equation  can be interpreted geometrically: if the solution curve (i.e. graph of a solution)
goes through the point
can be interpreted geometrically: if the solution curve (i.e. graph of a solution)
goes through the point  , then it holds that
, then it holds that  , i.e. we can find the slopes of the tangents of the curve even
if we do not know the solution itself. Direction field or slope field is a vector field
, i.e. we can find the slopes of the tangents of the curve even
if we do not know the solution itself. Direction field or slope field is a vector field  drawn through the points
drawn through the points  . The direction field provides a fairly accurate image of the behavior of the solution curves.
. The direction field provides a fairly accurate image of the behavior of the solution curves.
1st Order Ordinary Differential Equations
A manifesting problem in the theory of differential equations is that there is only a relatively small amount of methods for finding solutions that are generally applicable. Even for a fairly simple differential equation a generalized formula does not usually exist, and especially for higher order differential equations it is rare to be able to find an analytic solution. For some equations it is possible, however, and here some of the most common cases are introduced.
Linear 1st order ODE
If a differential equation is of the form
then it is called a linear differential equation. The left side of the equation is a linear combination of the derivatives with multipliers  . Thus a first order linear ODE is of the form
. Thus a first order linear ODE is of the form
If  for all
for all  , then the equation is called homogeneous. Otherwise the equation is nonhomogeneous.
, then the equation is called homogeneous. Otherwise the equation is nonhomogeneous.
Theorem 1.
Consider a normal form initial value problem
If the functions  and
and  are continuous in the interval
are continuous in the interval  containing the initial point
containing the initial point  , then the initial value problem has a unique solution.
, then the initial value problem has a unique solution.
The condition concerning the normality of the equation is crucial. For example, the equation  may have either zero or an infinite number of solutions depending on the initial condition: substituting
may have either zero or an infinite number of solutions depending on the initial condition: substituting  to the equation automatically forces the initial condition
to the equation automatically forces the initial condition  .
.
Solving a 1st order linear ODE
A first order linear ODE can be solved by using an integrating factor method. The idea of the method is to multiply both sides of the equation
 by the integrating factor
by the integrating factor  , which allows the equation to be written in the form
, which allows the equation to be written in the form
Integrating both sides of the equation, we get
It is not advisable to try to remember the formula as it is, but rather keep in mind the
idea of how the equation should be modified in order to proceed.
Example 1.
Let us solve the differential equation  The integrating factor is
The integrating factor is  so we multiply both sides by this expression:
so we multiply both sides by this expression:
Example 2.
Let us solve the initial value problem
First, we want to express the problem in normal form:
Now the integrating factor is  Hence, we get
Hence, we get
We have found the general solution. Because
 that is, the value of the function does not equal the given initial value, the problem does not have a solution.
The main reason for this is that the initial condition is given at
that is, the value of the function does not equal the given initial value, the problem does not have a solution.
The main reason for this is that the initial condition is given at  , where the normal form of the equation is not defined. Any other choice for
, where the normal form of the equation is not defined. Any other choice for  will lead to a
unique solution.
will lead to a
unique solution.
Example 3.
Let us solve the ODE  given the initial conditions
given the initial conditions
From the form  we see that the equation in question is a linear ODE. The integrating factor is
we see that the equation in question is a linear ODE. The integrating factor is

Multiplying by the integrating factor, we get

so the general solution to the ODE is  . From the initial value
. From the initial value  it follows that
it follows that
 , but the other condition
, but the other condition  leads to a contradiction
leads to a contradiction  .
Therefore, the solution in the (a) part is
.
Therefore, the solution in the (a) part is  , but a solution satisfying the initial condition of part b) does not exist: by substituting
, but a solution satisfying the initial condition of part b) does not exist: by substituting  ,
the equation forces
,
the equation forces  .
.
A first order linear ODE can be solved by using an integrating factor method. The idea of the method is to multiply both sides of the equation
 by the integrating factor
by the integrating factor  , which allows the equation to be written in the form
, which allows the equation to be written in the form
Integrating both sides of the equation, we get
It is not advisable to try to remember the formula as it is, but rather keep in mind the idea of how the equation should be modified in order to proceed.
Example 1.
Let us solve the differential equation  The integrating factor is
The integrating factor is  so we multiply both sides by this expression:
so we multiply both sides by this expression:
Example 2.
Let us solve the initial value problem
First, we want to express the problem in normal form:
Now the integrating factor is  Hence, we get
Hence, we get
We have found the general solution. Because
 that is, the value of the function does not equal the given initial value, the problem does not have a solution.
The main reason for this is that the initial condition is given at
that is, the value of the function does not equal the given initial value, the problem does not have a solution.
The main reason for this is that the initial condition is given at  , where the normal form of the equation is not defined. Any other choice for
, where the normal form of the equation is not defined. Any other choice for  will lead to a
unique solution.
will lead to a
unique solution.
Example 3.
Let us solve the ODE  given the initial conditions
given the initial conditions
From the form  we see that the equation in question is a linear ODE. The integrating factor is
we see that the equation in question is a linear ODE. The integrating factor is

Multiplying by the integrating factor, we get

so the general solution to the ODE is  . From the initial value
. From the initial value  it follows that
it follows that
 , but the other condition
, but the other condition  leads to a contradiction
leads to a contradiction  .
Therefore, the solution in the (a) part is
.
Therefore, the solution in the (a) part is  , but a solution satisfying the initial condition of part b) does not exist: by substituting
, but a solution satisfying the initial condition of part b) does not exist: by substituting  ,
the equation forces
,
the equation forces  .
.
Separable equation
A first order differential equation is separable, if it can be written in the form  where
where
 and
and  are integrable functions in the domain of interest. Treating formally
are integrable functions in the domain of interest. Treating formally  as a fraction, multiplying by
as a fraction, multiplying by  and dividing by
and dividing by
 , we obtain
, we obtain  .
Integrating the left hand side with respect to
.
Integrating the left hand side with respect to  and the right hand side with respect to
and the right hand side with respect to  , we get
, we get
This method gives the solution to the differential equation in implicit form, which we may further be able to solve explicitly for  . The justification for this formal treatment can be made by using change of variables in integrals.
. The justification for this formal treatment can be made by using change of variables in integrals.
Example 4.
Let us solve the differential equation  by separating the variables. (We could also solve the equation by using the method of integrating factors.)
by separating the variables. (We could also solve the equation by using the method of integrating factors.)
In the last step, we wrote  for simplicity. The case
for simplicity. The case  is also allowed, since it leads to the trivial solution
is also allowed, since it leads to the trivial solution  , see below.
, see below.
Example 5.
Let us solve the initial value problem
Because the general solution is not required, we may take a little shortcut by applying integrals in the following way:
The trivial solutions of a separable ODE
General solution achieved by applying the method for separable functions typically lacks information about solutions related to the zeros of the function  .
The reason for this is that in the separation method we need to assume that
.
The reason for this is that in the separation method we need to assume that  in order to be able to divide the expression by
in order to be able to divide the expression by  .
We notice that for each zero
.
We notice that for each zero  of the function
of the function  there exists a corresponding constant solution
there exists a corresponding constant solution  of the ODE
of the ODE  , since
, since
 . These solutions are called trivial solutions (in contrast to the general solution).
. These solutions are called trivial solutions (in contrast to the general solution).
If the conditions of the following theorem hold, then all the solutions to a separable differential equation can be derived from either the general solution or the trivial solutions.
Theorem 2.
Let us consider the initial value problem  .
.
- If
 is continuous (as a function of two variables), then there exists at least one solution in some interval containing the point
is continuous (as a function of two variables), then there exists at least one solution in some interval containing the point  .
. - Also, if
 is continuously differentiable with respect to
is continuously differentiable with respect to  , then the solution satisfying the initial condition is unique.
, then the solution satisfying the initial condition is unique. - The uniqueness also holds, when in addition to (i) the function
 is continuously differentiable with respect to
is continuously differentiable with respect to  and
and  .
.
The proof of the theorem is based on a technique known as Picard-Lindelöf iteration, which was invented by Emile Picard and further developed by the Finnish mathematician Ernst Lindelöf (1870-1946), and others.
Applying the previous theorem, we can formulate the following result for separable equations.
Theorem 3.
Let us consider a separable differential equation  , where
, where  is continuous and
is continuous and  is continuously differentiable.
is continuously differentiable.
The solution curves at each point  of the domain of the equation are always unique. In particular, the curves cannot intersect and it is not possible
for a single curve to split into two or several parts.
of the domain of the equation are always unique. In particular, the curves cannot intersect and it is not possible
for a single curve to split into two or several parts.
∴ The other solution curves of the ODE cannot intersect the curves  corresponding to the trivial solutions. That is, for all the other solutions the condition
corresponding to the trivial solutions. That is, for all the other solutions the condition
 automatically holds!
automatically holds!
Example 6.
Let us solve the linear homogeneous differential equation  by applying the method of separation.
by applying the method of separation.
The equation has the trivial solution  . Since the other solutions do not get the value 0 anywhere, it holds that
. Since the other solutions do not get the value 0 anywhere, it holds that
Here, the expression  has been replaced by a simpler constant
has been replaced by a simpler constant  .
.
 Equations expressible as separable
Equations expressible as separable
Some differential equations can made separable by using a suitable substitution.
i) ODEs of the form 
Example 7.
Let us solve the differential equation  The equation is not separable in this form, but we can make if separable by substituting
The equation is not separable in this form, but we can make if separable by substituting
 resulting to
resulting to  We get
We get
Separating the variables and integrating both sides, we get
Substituting  and simplifying yields
and simplifying yields
Here, it is not possible to derive an expression for y so we have to make do with just the implicit solution. The solutions can be visualized graphically:
As we can see, the solutions are spirals expanding in the positive direction that are suitably cut for demonstration purposes. This is clear from the solutions' polar coordinate representation which we obtain by using the substitution
Hence, the solution is
ii) ODEs of the form 
Another type of differential equation that can be made separable are equations of the form
To rewrite the equation as separable, we use the substitution 
Example 8.
Let us find the solution to the differential equation
Another type of differential equation that can be made separable are equations of the form
To rewrite the equation as separable, we use the substitution 
Example 8.
Let us find the solution to the differential equation
 Euler's method
Euler's method
In practice, it is usually not feasible to find analytical solutions to differential equations. In these cases, the only choice for us is to resort to numerical methods. A prominent example of this kind of technique is called Euler's method. The idea behind the method is the observation made earlier with direction fields: even if we do not know the solution itself, we are still able to determine the tangents of the solution curve. In other words, we are seeking solutions for the initial value problem
In Euler's method, we begin the solving process by choosing the step length  and using the iteration formula
and using the iteration formula
The iteration starts from the index  by substituting the given initial value to the right side of the iteration formula.
Since
by substituting the given initial value to the right side of the iteration formula.
Since  is the slope of the tangent of the solution at
is the slope of the tangent of the solution at  , on each step we move the distance expressed by the step length in the direction of the
tangent. Because of this, an error occurs, which grows as the step length is increased.
, on each step we move the distance expressed by the step length in the direction of the
tangent. Because of this, an error occurs, which grows as the step length is increased.
Example 9.
Use the gadget on the right to examine the solution to the initial value problem
obtained by using Euler's method and compare the result to the precise solution.
2nd and higher order ODEs
For higher order differential equations it is often impossible to find analytical solutions. In this section, we introduce some special cases for which analytical solutions can be found. Most of these cases are linear differential equations. Our focus is on second order differential equations, as they are more common in practical applications and for them it is more likely for an analytical solution to be found, compared to third or higher order differential equations.
Solving a homogeneous ODE
For second order linear equations, there is no easy way to find a general solution. We begin by examining a homogeneous equation
where  and
and  are continuous functions on their domains. Then, it holds that
are continuous functions on their domains. Then, it holds that
1) the equation has linearly independent solutions  and
and  , called fundamental solutions. Roughly speaking, linear independence means that the ratio
, called fundamental solutions. Roughly speaking, linear independence means that the ratio  is not constant, so that the solutions are essentially different from each other.
is not constant, so that the solutions are essentially different from each other.
2) the general solution can expressed by means of any linearly independent pair of solutions in the form  , where
, where  and
and  are constants.
are constants.
3) if the initial values  are fixed, then the solution is unique.
are fixed, then the solution is unique.
A general method for finding explicitly the fundamental solutions  and
and  does not exist. To find the solution, a typical approach is to try to make an educated guess about the solution's form and check the details by substituting this into the equation.
does not exist. To find the solution, a typical approach is to try to make an educated guess about the solution's form and check the details by substituting this into the equation.
The above results can be generalized to higher order homogeneous equations as well, but then the number of required fundamental solutions and initial conditions increases with respect to the order of the equation.
Example 1.
The equation  has solutions
has solutions  and
and  These solutions are linearly independent, so the general solution is of the form
These solutions are linearly independent, so the general solution is of the form 
Equations with constant coefficients
As a relatively simple special case, let us consider the 2nd order equation
In order to solve the equation, we use the guess  , where
, where  is an unknown constant. Substituting the guess into the equation yields
is an unknown constant. Substituting the guess into the equation yields
The last equation is called the characteristic equation of the ODE. Solving the characteristic equation allows us to find the solutions for the actual ODE. The roots of the characteristic equation can be divided into three cases:
1) The characteristic equation has two distinct real roots. Then, the ODE has the solutions  and
and 
2) The characteristic equation has a double root. Then, the ODE has the solutions  and
and 
3) The roots of the characteristic equation are of the form  Then, the ODE has the solutions
Then, the ODE has the solutions  and
and 
The second case can be justified by substitution into the original ODE, and the third case by using the Euler formula  . With minor changes, these results can also be generalized to higher order differential equations.
. With minor changes, these results can also be generalized to higher order differential equations.
Since the characteristic equation has exactly the same coefficients as the original ODE, it is not necessary to derive it again in concrete examples: just write it down by looking at the ODE!
Example 2.
Let us solve the initial value problem
The characteristic equation is  which has the roots
which has the roots  and
and  Thus, the general solution is
Thus, the general solution is  The constants can be determined by using the initial conditions:
The constants can be determined by using the initial conditions:
Hence, the general solution is 
Example 3.
Let us have a look at how the above results hold in higher order equations by solving
Now, the characteristic equation is  which has the roots
which has the roots  and
and  Thus, the fundamental solutions to the ODE are
Thus, the fundamental solutions to the ODE are  ,
,  ,
,  and
and  . The general solution is
. The general solution is
For second order linear equations, there is no easy way to find a general solution. We begin by examining a homogeneous equation
where  and
and  are continuous functions on their domains. Then, it holds that
are continuous functions on their domains. Then, it holds that
1) the equation has linearly independent solutions  and
and  , called fundamental solutions. Roughly speaking, linear independence means that the ratio
, called fundamental solutions. Roughly speaking, linear independence means that the ratio  is not constant, so that the solutions are essentially different from each other.
is not constant, so that the solutions are essentially different from each other.
2) the general solution can expressed by means of any linearly independent pair of solutions in the form  , where
, where  and
and  are constants.
are constants.
3) if the initial values  are fixed, then the solution is unique.
are fixed, then the solution is unique.
A general method for finding explicitly the fundamental solutions  and
and  does not exist. To find the solution, a typical approach is to try to make an educated guess about the solution's form and check the details by substituting this into the equation.
does not exist. To find the solution, a typical approach is to try to make an educated guess about the solution's form and check the details by substituting this into the equation.
The above results can be generalized to higher order homogeneous equations as well, but then the number of required fundamental solutions and initial conditions increases with respect to the order of the equation.
Example 1.
The equation  has solutions
has solutions  and
and  These solutions are linearly independent, so the general solution is of the form
These solutions are linearly independent, so the general solution is of the form 
Equations with constant coefficients
As a relatively simple special case, let us consider the 2nd order equation
In order to solve the equation, we use the guess  , where
, where  is an unknown constant. Substituting the guess into the equation yields
is an unknown constant. Substituting the guess into the equation yields
The last equation is called the characteristic equation of the ODE. Solving the characteristic equation allows us to find the solutions for the actual ODE. The roots of the characteristic equation can be divided into three cases:
1) The characteristic equation has two distinct real roots. Then, the ODE has the solutions  and
and 
2) The characteristic equation has a double root. Then, the ODE has the solutions  and
and 
3) The roots of the characteristic equation are of the form  Then, the ODE has the solutions
Then, the ODE has the solutions  and
and 
The second case can be justified by substitution into the original ODE, and the third case by using the Euler formula  . With minor changes, these results can also be generalized to higher order differential equations.
. With minor changes, these results can also be generalized to higher order differential equations.
Since the characteristic equation has exactly the same coefficients as the original ODE, it is not necessary to derive it again in concrete examples: just write it down by looking at the ODE!
Example 2.
Let us solve the initial value problem
The characteristic equation is  which has the roots
which has the roots  and
and  Thus, the general solution is
Thus, the general solution is  The constants can be determined by using the initial conditions:
The constants can be determined by using the initial conditions:
Hence, the general solution is 
Example 3.
Let us have a look at how the above results hold in higher order equations by solving
Now, the characteristic equation is  which has the roots
which has the roots  and
and  Thus, the fundamental solutions to the ODE are
Thus, the fundamental solutions to the ODE are  ,
,  ,
,  and
and  . The general solution is
. The general solution is
Example 4.
Let  be a constant. The characteristic equation of
the ODE
be a constant. The characteristic equation of
the ODE
 is
is  with roots
with roots  .
So
.
So  and
and  in Case 3). Since this ODE is
a model for harmonic oscillation, we use time
in Case 3). Since this ODE is
a model for harmonic oscillation, we use time  as variable, and obtain
the general solution
as variable, and obtain
the general solution
 with
with  constants. They will be uniquely determined if we know
the initial location
constants. They will be uniquely determined if we know
the initial location  and the initial velocity
and the initial velocity  . All solutions
are periodic and their period is
. All solutions
are periodic and their period is  . In the animation to the right we have
. In the animation to the right we have  and you can choose
and you can choose  and the initial displacement
and the initial displacement  .
.
Euler's differential equation
Another relatively common type of 2nd order differential equation is Euler's differential equation
where  and
and  are constants. An equation of this form is solved by using the guess
are constants. An equation of this form is solved by using the guess  . Substituting the guess in the equation yields
. Substituting the guess in the equation yields
Using the roots of this equation, we obtain the solutions for the ODE in the following way:
1) If the roots are distinct and real, then  and
and  .
.
2) If the equation has a double root, then  and
and  .
.
3) If the equation has roots of the form  , then
, then  and
and  .
.
Example 5.
Let us solve the equation  Noticing that the equation is Euler's differential equation, we proceed by using the guess
Noticing that the equation is Euler's differential equation, we proceed by using the guess  Substituting the guess into the equation, we get
Substituting the guess into the equation, we get  which yields
which yields  Therefore, the general solution to the ODE is
Therefore, the general solution to the ODE is
Another relatively common type of 2nd order differential equation is Euler's differential equation
where  and
and  are constants. An equation of this form is solved by using the guess
are constants. An equation of this form is solved by using the guess  . Substituting the guess in the equation yields
. Substituting the guess in the equation yields
Using the roots of this equation, we obtain the solutions for the ODE in the following way:
1) If the roots are distinct and real, then  and
and  .
.
2) If the equation has a double root, then  and
and  .
.
3) If the equation has roots of the form  , then
, then  and
and  .
.
Example 5.
Let us solve the equation  Noticing that the equation is Euler's differential equation, we proceed by using the guess
Noticing that the equation is Euler's differential equation, we proceed by using the guess  Substituting the guess into the equation, we get
Substituting the guess into the equation, we get  which yields
which yields  Therefore, the general solution to the ODE is
Therefore, the general solution to the ODE is
Nonhomogeneous linear differential equations
The general solution to a nonhomogeneous equation
is the general solution to the corresponding homogeneous equation  particular solution to the nonhomogeneous equation, i.e.
particular solution to the nonhomogeneous equation, i.e.
The particular solution  is usually found by using a guess that is of the same form as
is usually found by using a guess that is of the same form as  with general coefficients. Substituting the guess into the ODE, we can solve these coefficients, but only if the guess is of the correct form.
with general coefficients. Substituting the guess into the ODE, we can solve these coefficients, but only if the guess is of the correct form.
In the table below, we have created a list of possible guesses for second order differential equations with constant coefficients. The form of the guess depends on what kind of elementary functions  consists of. If
consists of. If  is a combination of several different elementary functions, then we need to include corresponding elements for all of these functions in our guess. The characteristic equation of the corresponding homogeneous differential equation is
is a combination of several different elementary functions, then we need to include corresponding elements for all of these functions in our guess. The characteristic equation of the corresponding homogeneous differential equation is  .
.
Note. For roots of a second degree polynomial we have to keep in mind that
Example 6.
Let us find the general solution to the ODE  , when
, when
The solutions are of the form  .
.
a) Substituting the guess  we get
we get
 ,
which solves for
,
which solves for  .
.
b) In this case a guess of the form  is useless, as it is part of the general solution to the corresponding homogeneous equation and yields just zero when substituted to the left side of the ODE. Here, a right guess is of the form
is useless, as it is part of the general solution to the corresponding homogeneous equation and yields just zero when substituted to the left side of the ODE. Here, a right guess is of the form  . Substitution yields
. Substitution yields

Using these values for  and
and  , we can write the general solutions to the given differential equations.
, we can write the general solutions to the given differential equations.
Example 7.
Let us find the solution to the ODE  with the initial conditions
with the initial conditions
 ,
,  .
.
Based on the previous example, the general solution is of the form
 . Differentiation yields
. Differentiation yields
 . From the initial conditions, we get the following pair of equations:
. From the initial conditions, we get the following pair of equations:

which solves for  and
and  . Therefore, the solution to the initial value problem is
. Therefore, the solution to the initial value problem is
 .
.
Example 8.
A typical application of a second order nonhomogeneous ODE is an RLC circuit containing a resistor (with resistance  ), an inductor (with inductance
), an inductor (with inductance  ), a capacitor (with capacitance
), a capacitor (with capacitance  ), and a time-dependent electromotive force
), and a time-dependent electromotive force  . The electric current
. The electric current  in the circuit satisfies the ODE
in the circuit satisfies the ODE  Let us solve this ODE with artificially chosen numerical values in the form
Let us solve this ODE with artificially chosen numerical values in the form 
The homogeneous part has characteristic equation of the form
 with solutions
with solutions  . This gives the solutions
. This gives the solutions  and
and  for the homogeneous equation. For a particular solution we try
for the homogeneous equation. For a particular solution we try  . Substituting this into the nonhomogeneous ODE and collecting similar terms yields to
. Substituting this into the nonhomogeneous ODE and collecting similar terms yields to  This equation will be
satisfied for all
This equation will be
satisfied for all  (only) if
(only) if

which solves for  and
and  . Therefore, the general solution is
. Therefore, the general solution is
 Note. The exponential terms go to zero very fast and eventually, the current oscillates in the form
Note. The exponential terms go to zero very fast and eventually, the current oscillates in the form 
The general solution to a nonhomogeneous equation
is the general solution to the corresponding homogeneous equation  particular solution to the nonhomogeneous equation, i.e.
particular solution to the nonhomogeneous equation, i.e.
The particular solution  is usually found by using a guess that is of the same form as
is usually found by using a guess that is of the same form as  with general coefficients. Substituting the guess into the ODE, we can solve these coefficients, but only if the guess is of the correct form.
with general coefficients. Substituting the guess into the ODE, we can solve these coefficients, but only if the guess is of the correct form.
In the table below, we have created a list of possible guesses for second order differential equations with constant coefficients. The form of the guess depends on what kind of elementary functions  consists of. If
consists of. If  is a combination of several different elementary functions, then we need to include corresponding elements for all of these functions in our guess. The characteristic equation of the corresponding homogeneous differential equation is
is a combination of several different elementary functions, then we need to include corresponding elements for all of these functions in our guess. The characteristic equation of the corresponding homogeneous differential equation is  .
.
Note. For roots of a second degree polynomial we have to keep in mind that
Example 6.
Let us find the general solution to the ODE  , when
, when
The solutions are of the form  .
.
a) Substituting the guess  we get
we get
 ,
which solves for
,
which solves for  .
.
b) In this case a guess of the form  is useless, as it is part of the general solution to the corresponding homogeneous equation and yields just zero when substituted to the left side of the ODE. Here, a right guess is of the form
is useless, as it is part of the general solution to the corresponding homogeneous equation and yields just zero when substituted to the left side of the ODE. Here, a right guess is of the form  . Substitution yields
. Substitution yields

Using these values for  and
and  , we can write the general solutions to the given differential equations.
, we can write the general solutions to the given differential equations.
Example 7.
Let us find the solution to the ODE  with the initial conditions
with the initial conditions
 ,
,  .
.
Based on the previous example, the general solution is of the form
 . Differentiation yields
. Differentiation yields
 . From the initial conditions, we get the following pair of equations:
. From the initial conditions, we get the following pair of equations:

which solves for  and
and  . Therefore, the solution to the initial value problem is
. Therefore, the solution to the initial value problem is
 .
.
Example 8.
A typical application of a second order nonhomogeneous ODE is an RLC circuit containing a resistor (with resistance  ), an inductor (with inductance
), an inductor (with inductance  ), a capacitor (with capacitance
), a capacitor (with capacitance  ), and a time-dependent electromotive force
), and a time-dependent electromotive force  . The electric current
. The electric current  in the circuit satisfies the ODE
in the circuit satisfies the ODE  Let us solve this ODE with artificially chosen numerical values in the form
Let us solve this ODE with artificially chosen numerical values in the form 
The homogeneous part has characteristic equation of the form
 with solutions
with solutions  . This gives the solutions
. This gives the solutions  and
and  for the homogeneous equation. For a particular solution we try
for the homogeneous equation. For a particular solution we try  . Substituting this into the nonhomogeneous ODE and collecting similar terms yields to
. Substituting this into the nonhomogeneous ODE and collecting similar terms yields to  This equation will be
satisfied for all
This equation will be
satisfied for all  (only) if
(only) if

which solves for  and
and  . Therefore, the general solution is
. Therefore, the general solution is
 Note. The exponential terms go to zero very fast and eventually, the current oscillates in the form
Note. The exponential terms go to zero very fast and eventually, the current oscillates in the form 


























































































































































































![c\in ]a,b[ c\in ]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/0eff8d69467c10b57a87a34915f5b2bd.gif)
![S:=\{x\in [a,b]: f(x)\lt s\} S:=\{x\in [a,b]: f(x)\lt s\}](https://mycourses.aalto.fi/filter/tex/pix.php/eacb7a7945e692016628d17fe60e5153.gif)

![S\subset [a,b] S\subset [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/1c4412382a7e6967fa515506b9ec2bbc.gif)
![c:=\sup(S)\in [a,b] c:=\sup(S)\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/5dc3d86393d63fe98ba4cf254eb1874f.gif)





![c+1/k\in [a,b]\setminus S c+1/k\in [a,b]\setminus S](https://mycourses.aalto.fi/filter/tex/pix.php/c2ea33254226bed6e819ab8c9354774f.gif)













![x_k\in [a,b] x_k\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/b4550c07770bd027aa227a5d7a44bbf8.gif)




![\lim_{j\to \infty}x_{k_{j}}= c \in [a,b] \lim_{j\to \infty}x_{k_{j}}= c \in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/0fafbfdfac0075be8df774f5e57e7659.gif)



![f\colon ]a,b[\to \mathbb{R} f\colon ]a,b[\to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/b877964696acedfc796cbe2d8af02c14.gif)
![f\colon ]0,1]\to \mathbb{R} f\colon ]0,1]\to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/1edd3f53fa21601c9c26312f91b77db5.gif)


![c,d\in [a,b] c,d\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/768405dea1bf3697b134e29f5fb7355c.gif)

![x\in [a,b] x\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/8290bddba5acf9822dcbf61f4ac67d1b.gif)


![y=\sup_{x\in [a,b]} f(x)>y-\frac{1}{k} y=\sup_{x\in [a,b]} f(x)>y-\frac{1}{k}](https://mycourses.aalto.fi/filter/tex/pix.php/b013411dfd804f02f65e8c2c55791353.gif)
![x_{k}\in [a,b] x_{k}\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/2a73f7d15bff135e06fed9829c845b98.gif)



![\lim_{j\to \infty}x_{k_{j}}=d\in [a,b] \lim_{j\to \infty}x_{k_{j}}=d\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/c52627f7ca86c7368161a63752761407.gif)








![[-1, 2] [-1, 2]](https://mycourses.aalto.fi/filter/tex/pix.php/dca4fcf792a3e27e8d0e6ffd6d3dc13c.gif)
![x_1,x_2\in [a,b] x_1,x_2\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/e19d698696d7ffab6b38c33a403d0f82.gif)
![f([a,b])=[f(x_1),f(x_2)] f([a,b])=[f(x_1),f(x_2)]](https://mycourses.aalto.fi/filter/tex/pix.php/d38dd7ed255a633b5f3b32a8b4251475.gif)












![\begin{aligned}\frac{(f+g)(x+h)-(f+g)(x)}{h} \ & \ = \ \frac{[f(x+h)+g(x+h)]-[f(x)+g(x)]}{h} \\ & \ = \ \frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\end{aligned} \begin{aligned}\frac{(f+g)(x+h)-(f+g)(x)}{h} \ & \ = \ \frac{[f(x+h)+g(x+h)]-[f(x)+g(x)]}{h} \\ & \ = \ \frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/ef8575955c1913eb61f3bda0de6c3ee8.gif)













![\begin{aligned}\frac{d}{dx} [(x^4-2)(2x+1)] &= \frac{d}{dx}(x^4-2) \cdot (2x+1) + (x^4-2) \cdot \frac{d}{dx}(2x + 1) \\ &= 4x^3(2x+1) + 2(x^4-2) \\ &= 8x^4+4x^3+2x^4-4 \\ &= 10x^4+4x^3-4.\end{aligned} \begin{aligned}\frac{d}{dx} [(x^4-2)(2x+1)] &= \frac{d}{dx}(x^4-2) \cdot (2x+1) + (x^4-2) \cdot \frac{d}{dx}(2x + 1) \\ &= 4x^3(2x+1) + 2(x^4-2) \\ &= 8x^4+4x^3+2x^4-4 \\ &= 10x^4+4x^3-4.\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/8c708f0f3c9ec809601fbd059363c2b4.gif)
![\frac{d}{dx} [(x^4-2)(2x+1)] = \frac{d}{dx} (2x^5 +x^4 -4x -2) = 10x^4 +4x^3 -4. \frac{d}{dx} [(x^4-2)(2x+1)] = \frac{d}{dx} (2x^5 +x^4 -4x -2) = 10x^4 +4x^3 -4.](https://mycourses.aalto.fi/filter/tex/pix.php/d030d685c2973158b90ad35a97a50d5b.gif)







![x_0\in \, ]a,b[ x_0\in \, ]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/b4b89672d69ecf8369f43f7dd31f0d2c.gif)

![]x_0-\delta,x_0+\delta[ ]x_0-\delta,x_0+\delta[](https://mycourses.aalto.fi/filter/tex/pix.php/c9bd44b465175498c9476b6701b55fca.gif)





![c\in \, ]x_0,x[ c\in \, ]x_0,x[](https://mycourses.aalto.fi/filter/tex/pix.php/5c97c28ce97d3f291e533efe3f450068.gif)


![\begin{aligned}\sin'(t) & = \lim_{h\to 0} \frac{\sin(t+h)-\sin(t)}{h} \\
& = \lim_{h\to 0} \frac{[\sin(t)\cos(h)+\cos(t)\sin(h)]-\sin(t)}{h} \\
& = \lim_{h\to 0}\sin(t)\frac{\cos(h)-1}{h}+\lim_{h\to 0}\cos(t)\frac{\sin(h)}{h}.
\end{aligned} \begin{aligned}\sin'(t) & = \lim_{h\to 0} \frac{\sin(t+h)-\sin(t)}{h} \\
& = \lim_{h\to 0} \frac{[\sin(t)\cos(h)+\cos(t)\sin(h)]-\sin(t)}{h} \\
& = \lim_{h\to 0}\sin(t)\frac{\cos(h)-1}{h}+\lim_{h\to 0}\cos(t)\frac{\sin(h)}{h}.
\end{aligned}](https://mycourses.aalto.fi/filter/tex/pix.php/43dab0c7e1606d265f8428433a47b025.gif)
























![\frac{f(g(x+h))-f(g(x))}{h}=[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}. \frac{f(g(x+h))-f(g(x))}{h}=[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}.](https://mycourses.aalto.fi/filter/tex/pix.php/4772424382ad3806e0cca96db8c05fd1.gif)

![[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}\to f'(g(x))g'(x). [E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}\to f'(g(x))g'(x).](https://mycourses.aalto.fi/filter/tex/pix.php/57e9195f36e9ff554cd408a7b174bd50.gif)

















![x_0\in [a,b] x_0\in [a,b]](https://mycourses.aalto.fi/filter/tex/pix.php/f1f8b7afdbcc5f31096799e43c43711e.gif)



































![f[A]=B f[A]=B](https://mycourses.aalto.fi/filter/tex/pix.php/c0dfc65c448fbf8cef4d8969eab57661.gif)




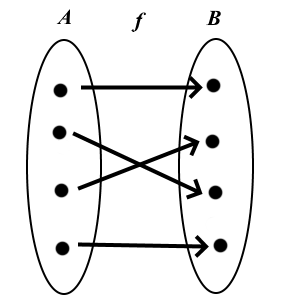
















![\sin \colon [-\pi/2,\pi/2]\to [-1,1]
\sin \colon [-\pi/2,\pi/2]\to [-1,1]](https://mycourses.aalto.fi/filter/tex/pix.php/8516ac159a27828b8807ae8346208684.gif)
![\cos \colon [0,\pi] \to [-1,1]
\cos \colon [0,\pi] \to [-1,1]](https://mycourses.aalto.fi/filter/tex/pix.php/7b6724fb6d58f64ba500defadc44773d.gif)
![\tan \colon ]-\pi/2,\pi/2[\, \to \mathbb{R}
\tan \colon ]-\pi/2,\pi/2[\, \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/04f0656b3b1805879518b5a4d600ae97.gif)
![\arctan \colon \mathbb{R}\to \ ]-\pi/2,\pi/2[, \arctan \colon \mathbb{R}\to \ ]-\pi/2,\pi/2[,](https://mycourses.aalto.fi/filter/tex/pix.php/5a0cfc94ec76b4bb98759ea997a6814e.gif)
![\arcsin \colon [-1,1]\to [-\pi/2,\pi/2], \arcsin \colon [-1,1]\to [-\pi/2,\pi/2],](https://mycourses.aalto.fi/filter/tex/pix.php/c4d09554c2fd5fc1cbf2d81a599c1b95.gif)
![\arccos \colon [-1,1]\to [0,\pi] \arccos \colon [-1,1]\to [0,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/ae1f9e9c619a7daceef40e2227521839.gif)
![x = \tan \alpha \Leftrightarrow \alpha = \arctan x \ \ \text{for } \alpha \in \ ]-\pi/2,\pi/2[ x = \tan \alpha \Leftrightarrow \alpha = \arctan x \ \ \text{for } \alpha \in \ ]-\pi/2,\pi/2[](https://mycourses.aalto.fi/filter/tex/pix.php/1e8adfc9de7373123d3e37d24295583b.gif)
![x = \sin \alpha \Leftrightarrow \alpha = \arcsin x \ \ \text{for } \alpha \in \, [-\pi/2,\pi/2] x = \sin \alpha \Leftrightarrow \alpha = \arcsin x \ \ \text{for } \alpha \in \, [-\pi/2,\pi/2]](https://mycourses.aalto.fi/filter/tex/pix.php/e0f134a17e198c541c553b3c2e9305f0.gif)
![x = \cos \alpha \Leftrightarrow \alpha = \arccos x \ \ \text{for } \alpha \in \, [0,\pi] x = \cos \alpha \Leftrightarrow \alpha = \arccos x \ \ \text{for } \alpha \in \, [0,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/eab3cb1a5193c48cde03e2046ec37027.gif)
















![\exp\colon\mathbb{R}\to\, ]0,\infty[ \exp\colon\mathbb{R}\to\, ]0,\infty[](https://mycourses.aalto.fi/filter/tex/pix.php/463736f26c065deb116e8539cc1e1c90.gif)

















![\ln\colon \ ]0,\infty[ \ \to \mathbb{R}
\ln\colon \ ]0,\infty[ \ \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/a57877163d9051a40ddff6a55fb8ea50.gif)














































![f\colon\left[-1,1\right] f\colon\left[-1,1\right]](https://mycourses.aalto.fi/filter/tex/pix.php/8fa1143ca458419d8b2c9fe6b3bc7b98.gif)













![p=\inf_{x\in\left[a,b\right]}f(x) p=\inf_{x\in\left[a,b\right]}f(x)](https://mycourses.aalto.fi/filter/tex/pix.php/df0ba13db5d97e1ab617c25bf3f053f3.gif)
![s=\sup_{x\in\left[a,b\right]}f(x) s=\sup_{x\in\left[a,b\right]}f(x)](https://mycourses.aalto.fi/filter/tex/pix.php/74dbac954365a4026b75091df793c18d.gif)





![c\in\,]a,b[ c\in\,]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/0645c1a33227f3466be2997827a643b5.gif)

![x\in\,]a,b[ x\in\,]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/72fa533e00aaedd77d6d52d82313b48e.gif)

![c\in\,[x,x+h] c\in\,[x,x+h]](https://mycourses.aalto.fi/filter/tex/pix.php/318888fc5bb357cd31a47f39bdaf0103.gif)
































![\left[x,x+\Delta x\right] \left[x,x+\Delta x\right]](https://mycourses.aalto.fi/filter/tex/pix.php/4d8fd407309f8f47e5b678de4fddac7f.gif)



![\left[a,\infty\right[,\left]-\infty,b\right] \left[a,\infty\right[,\left]-\infty,b\right]](https://mycourses.aalto.fi/filter/tex/pix.php/6d8fe0a29c1bae92fcd9c6684a5d437c.gif)































































































































