Python-oppimateriaali (CHEM-A2600)
| Site: | MyCourses |
| Course: | CHEM-A2600 - Kemiantekniikan ohjelmointikurssi, Luento-opetus, 5.9.2022-2.12.2022 |
| Book: | Python-oppimateriaali (CHEM-A2600) |
| Printed by: | Guest user |
| Date: | Wednesday, 19 February 2025, 12:13 AM |
Table of contents
- 1. Kierros 1
- 1.1. Tulostaminen (print) ja syötteen lukeminen (input)
- 1.2. Muuttujat
- 1.3. Aritmeettiset perusoperaatiot
- 1.4. Tyyppimuunnokset
- 1.5. Lukuarvojen pyöristäminen (round)
- 1.6. if-elif-else ja vertailuoperaattorit
- 1.7. Totuusmuuttujat
- 1.8. Loogiset operaattorit
- 1.9. Laskujärjestyksestä
- 1.10. while-silmukka
- 1.11. for-silmukka ja range
- 2. Kierros 2
- 3. Kierros 3
- 4. Kierros 4
- 5. Kierros 5
- 6. Kierros 6: SciPy
- 7. Kierros 6: Olio-ohjelmointi
- 8. Lisämateriaalia
Oppimateriaalin lisenssi
![]() Creative Commons Attribution-ShareAlike 4.0 International License.
Creative Commons Attribution-ShareAlike 4.0 International License.
Oppimateriaalin tekijät: Antti Karttunen (2016-2022), Tarmo Nieminen (2018), Julia Tofferi (2020), Riku Holopainen (2021)
Kierros 1
Kurssin ensimmäisellä kierroksella tutustutaan ohjelmoinnin peruskäsitteisiin ja Python-ohjelmointikielen perusteisiin.
1. Anaconda-jakelupaketin asentaminen
Ohjelmointitehtävien tekemiseksi tarvitset esimerkiksi Anaconda-jakelupaketin ja Spyder-ohjelmointiympäristön. Oppimateriaalin Lisämateriaalia-luku sisältää Anacondan asennusohjeen ja Spyderin käyttöohjeita.
2. Oppimateriaalin lukuohje
Kun oppimateriaalissa esitetään Python-koodia, se näyttää tältä:
print("Nyt lasketaan!")
print("11*11 on", 11*11)
Kun oppimateriaalissa näytetään, mitä Python-koodi tulostaa, se näyttää tältä:
Nyt lasketaan! 11 * 11 on 121
3. Oppimateriaalin esimerkkiohjelmien kokeileminen itse
- Kopioi esimerkkiohjelman koodi Spyder-editoriin.
- Aja koodi painamalla Spyderissä vihreää "Run"-painiketta tai F5-nappia.
- Esimerkkiohjelmien kokeileminen ja muokkaaminen on erittäin suositeltavaa, koska se helpottaa merkittävästi esimerkkien ymmärtämistä.
4. Ohjelmakoodin kommentointi
Ohjelmien huolellinen kommentointi on ensiarvoisen tärkeää, jotta:
- Muut ymmärtävät, mitä kirjoittamasi koodi tekee
- Muistat itse, mitä kirjoittamasi koodi tekee!
Ohjelmakoodiin voi lisätä kommentteja #-merkin jälkeen:
# Aloitetaan!
print("Eka ohjelmani")
# Jatketaan!
print("Moi!") # Rivin loppuun voi myös lisätä kommentteja
Ylläoleva ohjelma tulostaisi:
Eka ohjelmani
Moi!
Huomaa, että kommentit eivät tulostuneet.
Monirivisiä kommentteja voi kirjoittaa """ kommentti """ –merkinnällä:
print("Eka ohjelmani")
"""
Olipa hieno kokemus!
Tämä on kolmerivinen välikommentti.
Sitten jatketaan!
"""
print("Moi!")
5. Muita Python-oppimateriaaleja
Lisämateriaalin Python-verkkomateriaaleja -kappaleessa on listattu hyviä verkosta löytyviä oppimateriaaleja, joita voi myös hyödyntää Python-ohjelmoinnin opettelussa. Jos pidät opiskelusta videomateriaalien avulla, sivulta löytyy linkkejä videomuotoisiin oppimateriaaleihin.
6. Jos olet aiemmin osallistunut kurssille Ohjelmoinnin peruskurssi Y1
Jos olet aiemmin osallistunut Aallon yleiselle Python-kurssille, tutustuthan lisämateriaalin kappaleeseen main-funktio ennen kuin aloitat tämän kurssin tehtävien tekemisen.
7. Oppimateriaalin sisältämät tehtävät
Oppimateriaali sisältää myös erilaisia tehtäviä, joilla voit tarkistaa, kuinka hyvin olet sisäistänyt oppimateriaalissa käsitellyt asiat.
Oppaassa olevien tehtävien tarkoitus on tukea oppimista, ne eivät vaikuta kurssin arvosteluun!
Alla on kaksi esimerkkiä oppimateriaalin tehtävätyypeistä.
Tehtävä 1.0.1
Tehtävä 1.0.2
Tulostaminen (print) ja syötteen lukeminen (input)
Tulostaminen print-funktiolla
Pythonissa voi tulostaa tietoa ruudulle print-funktiolla:
# Tulostetaan merkkijono "Terve!"
print("Terve!")
tulostaa:
Terve!
(Funktioiden toimintaperiaatteisiin perehdymme tarkemmin kurssin toisella kierroksella. Nyt ensimmäisellä kierroksella hyödynnämme vain muutamia Pythonin sisäänrakennettuja funktioita, joiden käyttö on yhtä suoraviivaista kuin print-funktion käyttö.)
Otetaan toinen esimerkki, jossa print-funktiolle annetaan useita eri arvoja pilkulla erotettuna. Se tulostaa molemmat arvot niin, että niiden välissä on välilyönti:
# Näin voimme tulostaa laskutoimitusten tuloksia
print("11*11 on", 11*11)tulostaa:
11*11 on 121
Laskutoimituksista: Halutessasi voit tehdä laskutoimituksia myös suoraan Spyderin Python-konsolissa. Kokeile kirjoittaa konsoliin esimerkiksi 5*5 ja paina Enter
Isot ja pienet kirjaimet
Pythonissa isot ja pienet kirjaimet ovat merkitseviä. Käsky print on siis eri asia kuin Print tai PRINT.
Käyttäjän syötteen lukeminen input-funktiolla
Käyttäjältä voi kysyä tietoja input-funktiolla:
# Kysytään käyttäjän nimeä
nimi = input("Mikä nimesi on?")
print("Hieno nimi sinulla", nimi)
Lopputulos:
Mikä nimesi on?Marsu
Hieno nimi sinulla Marsu
Esimerkissä siis input-funktiolla kysytään käyttäjältä nimeä ja käyttäjän antama merkkijono tallennetaan muuttujaan nimi. Sen jälkeen muuttujan arvo voidaan tulostaa print-funktion avulla. Muuttujiin voidaan säilöä tietoa ja niistä kerrotaan lisää seuraavassa luvussa.
Kysymys ja vastaus tulostuvat selkeämmin, jos lisätään välilyönti merkkijonon loppuun:
nimi = input("Mikä nimesi on? ")
print("Hieno nimi sinulla", nimi)
Lopputulos:
Mikä nimesi on? Marsu
Hieno nimi sinulla Marsu
Kaikkein selkeintä on yleensä käyttää rivinvaihtoa "\n" kysymyksen lopussa
nimi = input("Mikä nimesi on?\n")
print("Hieno nimi sinulla", nimi)
Lopputulos (Huom! Tästä lähtien käyttäjän input-funktiolle antama syöte merkitään ">"-merkillä):
Mikä nimesi on?
> Marsu
Hieno nimi sinulla Marsu
Kolmas esimerkki, jossa kysytään kaksi eri tietoa ja tulostetaan ne molemmat:
nimi = input("Mikä nimesi on?\n")
kaveri = input("Mikä kaverisi nimi on?\n")
print("Mukava tavata", nimi, "ja", kaveri)
Lopputulos:
Mikä nimesi on?
> Marsu
Mikä kaverisi nimi on?
> Jomppa
Mukava tavata Marsu ja Jomppa
Tärkeää: input-funktio palauttaa aina merkkijonon
input-funktio lukee käyttäjältä aina ns. merkkijonon (engl. string). Tämä koodi:
luku = input("Anna luku niin kerron sen kahdella:\n")
print("Antamasi luku", luku, "kerrottuna kahdella on", 2 * luku)
ei siis annakaan odotettua lopputulosta:
Anna luku niin kerron sen kahdella: > 5 Antamasi luku 5 kerrottuna kahdella on 55
Tämä ongelma ratkeaa seuraavassa luvussa, jossa opimme käsitteet muuttuja ja muuttujan tyyppi.
input-funktio CodeRunner-tehtävissä
CodeRunner-tehtävissä input-funktion kysymystä (esim. "Anna nimi: \n") ei tarkasteta, mutta kannattaa käyttää selkeitä kysymyksiä, jotta kirjoittamasi koodi on selkeää ja luettavaa.
Lisätietoa print-funktiosta: Rivinvaihdot ja end-parametri
print-funktio lisää tekstin loppuun oletuksena rivinvaihdon "\n". Niitä voi myös tulostaa itse lisää:
# Tulostetaan kaksi alkuainesymbolia ja kolme rivinvaihtoa ("\n")
print("Jaloja kaasuja: He ja Ne\n\n\n")
# Tulostetaan pari kaasua lisää
print("Ja lisäksi: Ar ja Kr")
Tulostaa
Jaloja kaasuja: He Ne
Ja lisäksi: Ar Kr
Rivinvaihdon voi muuttaa joksikin muuksi merkiksi print-funktion end-parametrillä:
print("Rivi 1.")
print("Rivi 2. Rivien väliin tuli rivinvaihto.")
print("Teksti 1.", end = " ")
print("Teksti 2. Tekstien väliin tuli välilyönti.")
tulostaa
Rivi 1.
Rivi 2. Rivien väliin tuli rivinvaihto.
Teksti 1. Teksti 2. Tekstien väliin tuli välilyönti.Tehtävä 1.1.1
Tehtävä 1.1.2
Muuttujat
Ohjelmoidessa tallennamme tietoa muuttujiin (engl. variable). Esimerkiksi input-funktio tallentaa tässä esimerkissä käyttäjän syötteen merkkijonona muuttujaan, jonka nimi on etunimi:
etunimi = input("Anna etunimesi\n")
Tavallisia muuttujatyyppejä Pythonissa ovat:
| Muuttujatyyppi | Nimi Pythonissa | Esimerkkejä | Kommentti |
|---|---|---|---|
| Merkkijono | str | "Hei!", 'OK' | Sekä "kaksinkertaiset" että 'yksinkertaiset' lainausmerkit toimivat. |
| Kokonaisluku | int | 2, 0, -2, 1924 | Positiiviset ja negatiiviset kokonaisluvut ja nolla |
| Liukuluku | float | 1.04, -3.0004 | Desimaaliluku |
| Kompleksiluku | complex | 2.0 + 3.0j | Emme käytä tällä kurssilla |
| Totuusarvo | bool | True tai False | Englannin kielen sanasta Boolean |
Muuttujiin voidaan sijoittaa arvoja "="-merkin avulla. Muutama esimerkki muuttujien käytöstä:
iso_luku = 50000005
print("Iso lukumme on", iso_luku)
pieni_luku = 0.0009
print("Pieni lukumme on", pieni_luku)
Ohjelma tulostaa:
Iso lukumme on 50000005
Pieni lukumme on 0.0009
Muuttuja iso_luku on ylläolevassa kokonaisluku, kun taas muuttuja pieni_luku on liukuluku.
Toisin kuin monissa muissa ohjelmointikielissä, Pythonissa muuttujan tyyppiä ei tarvitse määritellä ennen muuttujan käyttämistä. Python päättelee muuttujan tyypin, kun muuttujan arvo asetetaan.
Merkkijonomuuttujien luominen
Esimerkki:
# Tyhjän merkkijonomuuttujan luominen: teksti = "" # Merkkijonomuuttujan alustaminen merkkijonolla: tervehdys = "Hei!" print(tervehdys)
tulostaa
Hei!
Muuttujien nimeäminen
Älä käytä muuttujien nimissä koskaan ääkkösiä (ä, ö, å) tai erikoismerkkejä (*, /, jne.)! Se johtaa ongelmiin.
Lukuarvojen yksikköjen huomiominen
Tieteellisessä laskennassa meidän pitää aina olla selvillä käytössä olevista yksiköistä. Python ei pidä mitenkään kirjaa muuttujan yksiköistä, vaan se on ohjelmoijan vastuulla. Onkin erittäin tärkeää kirjata yksiköt aina muistiin kommentteina. Esimerkiksi:
# Tehtävän lähtöarvot n = 0.334 # ainemäärä, mol V = 0.014 # tilavuus, m^3 p = 101325 # paine, Pa
On erittäin suositeltavaa pitää kaikki lukuarvot SI-yksiköissä aina kun mahdollista.
Lisätietoa: Liukulukujen tieteellinen merkintätapa
Pythonissa voi käyttää myös tieteellistä merkintätapaa, missä 2e5 tarkoittaa 2 * 105. Esimerkki:
tosi_pieni = 0.0000002
print("Luku on:", tosi_pieni)
Tulostaa
Luku on: 2e-07
Tehtävä 1.2.1
Aritmeettiset perusoperaatiot
Laskutoimituksia varten Python tarjoaa mm. seuraavat operaatiot:
| Operaattori | Operaatio | Kokeile Python-konsolissa |
|---|---|---|
| + | Yhteenlasku | 5 + 5 |
| - | Vähennyslasku | 1000 - 4 |
| * | Kertolasku | 11 * 11 |
| / | Jakolasku | 11 / 5 (tulos = 2.2, eli float) |
| // | Katkaiseva jakolasku | 11 // 5 (tulos = 2, eli int) |
| % | Jakojäännös | 11 % 5 (tulos = 1, eli int) |
| ** | Potenssiin korotus | 2 ** 4 |
| abs(x) | Itseisarvo | abs(4-16) |
Laskujärjestyksen säätäminen sulkumerkeillä
Laskujärjestystä voi säätää kaarisulkeilla:
print(2 ** (2 + 2)) print(2 ** 2 + 2)
tulostaa:
16
6
Merkkijonojen yhdistäminen toisiinsa
Merkkijonoja voi yhdistää yhteenlaskuoperaattorilla:
print("Lappeen" + "ranta")
tulostaa
Lappeenranta
Merkkijonojen kertominen kokonaisluvuilla
Merkkijonon (string) saa kertoa kokonaisluvulla (int):
print("tip tap" * 5)
tulostaa
tip tap tip tap tip tap tip tap tip tap
Kokonaislukujen jaollisuuden testaaminen
Jakojäännösoperaattorilla on kätevä testata kokonaislukujen jaollisuutta:
luku = 6 if luku % 3 == 0:
print("Luku on kolmella jaollinen")
tulostaa
Luku on kolmella jaollinenLyhennetyt laskuoperaatiot
Pythonissa voi käyttää myös lyhennettyjä laskuoperaatioita +=, -=, *= ja /=
# Annetaan muuttujalle n alkuarvo n = 10 # Sama kuin: n = n + 1 (eli n on nyt 11) n += 1 # Sama kuin: n = n - 1 (eli n on nyt 10) n -= 1 # Sama kuin: n = n * 2 (eli n on nyt 20) n *= 2 # Sama kuin: n = n / 2 (eli n on nyt 10.0) n /= 2
On puhdas makuasia, kumpaa muotoa haluaa käyttää, pitkää vai lyhyttä. Pitkä on aloittelijalle selkeämpi valinta.
Tehtävä 1.3.1
Tyyppimuunnokset
Monesti on tarpeen muuntaa muuttujia yhdestä tyypistä toiseen.
Merkkijonon muuntaminen lukuarvoiksi
Merkkijonon (str) voi muuntaa kokonaisluvuksi int-funktiolla ja liukuluvuksi float-funktiolla:
luku_str = "2"
print("luku_str * 2 on:", luku_str * 2)
luku_int = int(luku_str)
print("luku_int * 2 on:", luku_int * 2)
luku_float = float(luku_str)
print("luku_float * 2 on:", luku_float * 2)
Lopputulos:
luku_str * 2 on: 22 luku_int * 2 on: 4 luku_float * 2 on: 4.0
Eli ensimmäinen "laskutoimitus" merkkijonoilla vain kaksinkertaistaa merkkijonon pituuden, mutta kaksi jälkimmäistä laskutoimitusta laskevat oikeasti kokonais- ja liukuluvuilla.
Merkkijonon muuntamista lukuarvoksi hyödynnämme varsinkin input-funktion käytön yhteydessä.
Kokonaislukujen kysyminen käyttäjältä input-funktiolla
input-funktio lukee käyttäjältä merkkijonon. Muunnetaan luettu merkkijono kokonaisluvuksi int-funktiolla:
luku = int(input("Anna luku niin kerron sen kahdella\n"))
print("Antamasi luku", luku, "kerrottuna kahdella on", 2 * luku)
Lopputulos (Muista, että ">"-merkki tarkoittaa käyttäjän input-funktiolle antamaa syötettä):
Anna luku niin kerron sen kahdella > 3 Antamasi luku 3 kerrottuna kahdella on 6
Liukulukujen kysyminen käyttäjältä input-funktiolla
Muunnetaan input-funktiolla luettu merkkijono suoraan liukuluvuksi float-funktiolla:
luku = float(input("Anna luku niin kerron sen luvulla 2.6\n"))
print("Antamasi luku", luku, "kerrottuna luvulla 2.6 on", 2.6 * luku)
Lopputulos:
Anna luku niin kerron sen luvulla 2.6
> 5
Antamasi luku 5.0 kerrottuna luvulla 2.6 on 13.0
Lukuarvojen muuntaminen merkkijonoksi
Liukuluvun tai kokonaisluvun voi muuntaa merkkijonoksi str-funktiolla:
mjono1 = str(5)
mjono2 = str(6.5)
print("Merkkijonojen mjono1 ja mjono2 yhdistelmä:", mjono1 + mjono2)
Lopputulos:
Merkkijonojen mjono1 ja mjono2 yhdistelmä: 56.5
Tehtävä 1.4.1
Lukuarvojen pyöristäminen (round)
Edellisessä luvussa opeteltiin lukemaan lukuarvoja input-funktiolla:
luku = float(input("Anna luku niin kerron sen numerolla 2.6\n"))
print("Antamasi luku", luku, "kerrottuna numerolla 2.6 on", 2.6 * luku)
Tarkastellaan, mitä tämä koodi tulostaa, kun annamme syötteeksi liukuluvun 3.0:
Anna luku niin kerron sen numerolla 2.6 3.0 Antamasi luku 3.0 kerrottuna numerolla 2.6 on 7.800000000000001
Miksi koodi tulostaa 7.800000000000001 eikä 7.8? Tämä johtuu tavasta, jolla tietokoneet käsittelevät liukulukuja (lisätietoa aiheesta kiinnostuneille Python-tutoriaalissa). Luonnollisesti meille riittäisi tässä tapauksessa yhden desimaalin tarkkuus. Tutustutaan seuraavaksi pyöristysfunktioon round.
round-funktio
Kokonaisluvun (int) muuntaminen liukuluvuksi (float) on yksinkertaista. Muunnetaan kokonaisluku 5 liukuluvuksi ja tulostetaan se:
print(float(5))
tulostaa
5.0
Mutta liukulukujen muuntamisessa kokonaisluvuiksi tulee olla tarkkana:
print(int(5.1)) print(int(5.9))
tulostaa
5 5
Liukuluvun suora muunnos int-funktiolla siis katkaisee liukuluvun desimaalipisteen kohdalta. Liukuluvun voi pyöristää lähimpään kokonaislukuun round-funktiolla:
print(round(5.1)) print(round(5.9))
tulostaa
5 6
Liukulukuja voi myös pyöristää haluttuun tarkkuuteen. round-funktion toinen parametri kertoo käytettävien desimaalien määrän:
print(round(5.666, 1)) print(round(5.666, 2))
tulostaa
5.7 5.67
round-funktiota voi siis hyödyntää, kun ilmoitamme liukulukulaskujen tuloksia käyttäjälle. Kierroksen 2 materiaalissa kerrotaan tutustumme muotoiltujen merkkijonojen tulostamiseen f-merkkijonoilla tai str.format-funktiolla. Niiden avulla liukulukujen pyöristäminen tulostamista varten on hyvin helppoa.
Huom! Älä koskaan pyöristä liukulukuja laskutoimitusten aikana! Liukuluvuilla työskennellään aina mahdollisimman suurella tarkkuudella ja ainoastaan käyttäjälle ilmoitettava luku pyöristetään johonkin ihmissilmälle sopivampaan tarkkuuteen. Ilmoitustarkkuuteen pätevät tässä samat säännöt kuin normaalistikin, eli tuloksen ilmoitustarkkuus riippuu esim. lähtöarvojen tarkkuudesta.
Lisätietoa: Kokonaislukujen pyöristäminen round-funktiolla
round-funktiolla on myös vähemmän tunnettu ominaisuus, jonka avulla voi helposti pyöristää lukuja haluttuun ilmoitustarkkuuteen myös desimaalipisteen vasemmalta puolen. Tätä ominaisuutta tarvitaan usein luonnontieteissä, kun mittaustarkkuus rajoittaa vastauksen tarkkuutta. Tällöin funktion toinen parametri annetaan negatiivisena:
print(round(5624, -3)) # tarkkuus: 10^3 print(round(5624, -2)) # tarkkuus: 10^2 print(round(5624, -1)) # tarkkuus: 10^1
tulostaa
6000 5600 5620
Tässä esimerkissä pyöristettiin siis kokonaislukuja haluttuun tarkkuuteen. Eli round-funktion toinen parametri ndigits tarkoittaa sekä positiivisten että negatiivisten lukujen kohdalla "pyöristä tarkkuuteen 10-ndigits".
Tehtävä 1.5.1
if-elif-else -ehtolauseet ja vertailuoperaattorit
if-ehtolauseen avulla ohjataan ohjelman suoritusta haluttuun suuntaan. if-ehtolauseen lyhyempi muoto on if-else:
if EHTO:
jos EHTO toteutuu, suoritetaan tässä sisennetty koodi
else:
jos EHTO ei toteudu, suoritetaan tässä sisennetty koodi
if-ehtolauseen pidempi muoto on if-elif-else:
if EHTO1:
jos EHTO1 toteutuu, suoritetaan tässä sisennetty koodi
elif EHTO2:
jos EHTO1 ei toteudu, mutta EHTO2 toteutuu, suoritetaan tässä sisennetty koodi
else:
jos EHTO1 tai EHTO2 ei toteudu, suoritetaan tässä sisennetty koodiHuomaa sisennykset: Pythonissa sisennykset ovat tärkeässä roolissa ja yllä olevat ehtolauseet eivät toimi, jos niitä ei ole sisennetty oikein.
Käydään ensin läpi ehtolauseissa käytettyjä vertailuoperaattoreita, jonka jälkeen siirrytään käytännön esimerkkeihin.
Vertailuoperaattorit
Ehtolauseissa käytetään hyvin usein vertailuoperaattoreita:
| Operaattori | Vertailuoperaattorin merkitys | Esimerkkejä ehtolauseessa |
|---|---|---|
| == | Yhtä suuri kuin | if numero == 1000: if nimi == "Tytti": |
| != | Erisuuri kuin | if hinta != 10: if vierailija != "Loiri": |
| > | Suurempi kuin | if massa > 55.5: |
| < | Pienempi kuin | if lampotla < 0.0: |
| >= | Suurempi tai yhtä suuri kuin | if paine >= 32: |
| <= | Pienempi tai yhtä suuri kuin | if tilavuus <= 24: |
if-else
Tarkastellaan esimerkkiohjelmaa:
luku = int(input("Anna kokonaisluku:\n"))
if luku >= 0:
print("Antamasi luku on suurempi tai yhtä suuri kuin nolla")
else:
print("Antamasi luku on pienempi kuin nolla")
Esimerkkisuoritus:
Anna kokonaisluku: > 5 Antamasi luku on suurempi tai yhtäsuuri kuin nolla
Toinen esimerkkisuoritus eri syötteellä:
Anna kokonaisluku:
> -222
Antamasi luku on pienempi kuin nolla
if-ehtolauseita voi olla useita sisäkkäin. Huomaa sisennysten käyttö tässä esimerkkiohjelmassa:
luku = int(input("Anna kokonaisluku:\n"))
if luku >= 0:
print("Antamasi luku on suurempi tai yhtäsuuri kuin nolla")
if luku > 1000:
print("Se on jopa suurempi kuin 1000")
else:
print("Se on kuitenkin enintään 1000")
else:
print("Antamasi luku on pienempi kuin nolla")
Esimerkkisuoritus:
Anna kokonaisluku: > 999 Antamasi luku on suurempi tai yhtäsuuri kuin nolla Se on kuitenkin enintään 1000
Ensimmäinen ehto "luku >= 0" siis toteutui, mutta ensimmäisen ehtolauseen sisällä oleva ehto "luku > 0" ei toteutunut.
if-elif-else
Ehtolauseeseen voi myös lisätä mielivaltaisen määrän lisäehtoja elif-käskyllä:
luku = int(input("Anna kokonaisluku: "))
if luku > 1000:
print("Antamasi luku on suurempi kuin tuhat")
elif luku > 100:
print("Antamasi luku on suurempi kuin sata")
elif luku > 10:
print("Antamasi luku on suurempi kuin kymmenen")
elif luku >= 0:
print("Antamasi luku on välillä 0..10")
else:
print("Antamasi luku on pienempi kuin nolla")
else-osio ei ole pakollinen:
kuukausi = input("Mikä kuukausi nyt on?\n")
if kuukausi == "joulukuu":
print("Joulu tulla jolkottaa")
elif kuukausi == "elokuu":
print("Vielä on kesää jäljellä")
Lisätietoja: Liukulukujen yhtäsuuruuden vertailu
Huom! Liukulukujen yhtäsuuruuden vertailun kanssa pitää olla tarkkana! Yhtäsuuruuden vertailu on parasta tehdä math.isclose-funktiolla. Palaamme tähän asiaan 2. kierroksen oppimateriaalissa.
Tehtävä 1.6.1
Tehtävä 1.6.2
Totuusmuuttujat
Ehtolauseissa hyödynnetään usein totuusmuuttujia (bool). Totuusmuuttujan arvo on joko True tai False, joten totuusmuuttujaan on kätevä tallentaa tieto siitä, onko joku ehto täyttynyt ja testata tätä ehtoa myöhemmin:
paine = float(input("Anna paine reaktorissa (bar):\n"))
# Jos paine on yli 1 bar, tallennetaan tieto totuusmuuttujaan ylipaine
if paine > 1.0:
ylipaine = True
else:
ylipaine = False
T = float(input("Anna lämpötila (K):\n"))
if T > 385.0:
if ylipaine:
print("Varoitus! Reaktorissa ylipaine ja korkea lämpötila")
else:
print("Olosuhteet OK")
Huomaa, miten totuusmuuttujaa ylipaine voi käyttää if-ehtolauseessa yksinkertaisesti muodossa
if ylipaine:
eikä tarvitse siis kirjoittaa
if ylipaine == True:
Tämä johtuu siitä, että if-ehtolauseen testin arvo on aina True tai False, joten totuusmuuttujan voi laittaa suoraan ehtolauseen testiksi.
Tehtävä 1.7.1
Loogiset operaattorit
Loogiset operaattorit toimivat yhdessä totuusmuuttujien kanssa.
not-operaattori
not-operaattorilla voi kääntää totuusmuuttujan arvon tai ehtolauseen ehdon päinvastaiseksi:
if not ylipaine:
print("Ei vaaraa ylipaineesta")
Toinen esimerkki:
alkuaine = input("Anna suosikkialkuaineesi symboli\n")
if not (alkuaine == "Au"):
print("Et taida olla alkemisti")
and-operaattori
and-operaattorilla voi yhdistää kaksi totuusmuuttujaa (tai ehtolauseen ehtoa). and-lauseen arvo on True, jos molempien ehtojen arvo on True:
if alkuaine1 == "Cu" and alkuaine2 == "O":
print("Kuparioksidi")
if ylipaine and T > 410.0:
print("Kriittiset olosuhteet!")
or-operaattori
or-operaattorilla voi myös yhdistää kaksi totuusmuuttujaa (tai ehtolauseen ehtoa). or-lauseen arvo on True, jos jommankumman ehdon arvo on True:
if kaasu == "He" or kaasu == "Ne":
print("Jalokaasu")
if T < 200.0 or T > 300.0:
print("Lämpötila ei ole optimaalinen reaktion kannalta")
# Ehtoja voi myös "ketjuttaa" useammalla or-lauseella:
if kaasu == "He" or kaasu == "Ne" or kaasu == "Ar":
print("Jalokaasu")
Loogisten ehtojen ryhmittely
Monimutkaisemmat ehdot on parasta ryhmitellä sulkujen avulla:
if massa > 200.0 or (tiheys > 22.59 and tilavuus > 10.0):
print("Kappale on liian painava")
Syventävää tietoa: lyhennetty tapa kirjoittaa vertailuja
Pythonissa voi myös yhdistää eri muuttujien vertailuja tavalla, joka on tuttu matematiikasta. Vertailulauseke
if 10 < luku and luku < 1000:
on mahdollista kirjoittaa myös lyhennetyssä muodossa:
if 10 < luku < 1000:
Jälkimmäinen versio siis "piilottaa" and-operaattorin. Lisätietoja aiheesta Pythonin virallisesta dokumentaatiossa
.
Tehtävä 1.8.1
Laskujärjestyksestä
Alla on Pythonin operaattorien "arvojärjestys" (operator precedence) heikoimmasta vahvimpaan:
| Operaattori | Merkitys |
|---|---|
| or | Looginen operaattori (boolean) |
| and | Looginen operaattori (boolean) |
| not | Looginen operaattori (boolean) |
| <, <=, >, >=, !=, == | Vertailuoperaattorit |
| +, - | Yhteen- ja vähennyslasku |
| *, /, //, % | Kerto- ja jakolasku |
| ** | Potenssiin nosto |
Huom! Ylläolevassa taulukossa on listattu vain tällä kurssilla käytettävät operaattorit. Täydellinen lista, joka sisältää esimerkiksi bittioperaatiot, löytyy osoitteesta https://docs.python.org/3/reference/expressions.html#operator-precedence
Aivan kuten matematiikassa, järjestystä voi säätää suluilla:
print(4 + 2 * 5) print((4 + 2) * 5)
Tulostaa
14
30
Loogiset operaattorit ovat siis heikoimpia operaattoreita. Huomaa niiden arvojärjestys: not on vahvempi kuin and, joka taas on vahvempi kuin or:
# Tulostaa False, koska 3 > 4 ei ole totta print(3 > 4) # Tulostaa True, koska 5 < 6 on totta print(3 > 4 or 5 < 6) # Tulostaa False, koska and on vahvempi kuin or ja 7 > 8 ei ole totta print(3 > 4 or 5 < 6 and 7 > 8) # Lausekkeen voisi siis selkeyden vuoksi kirjoittaa myös # 3 > 4 or (5 < 6 and 7 > 8) # Tulostaa True, koska not kääntää ehdon 7 > 8 arvosta False arvoon True print(3 > 4 or (5 < 6 and not 7 > 8))
Tehtävä 1.9.1
while-silmukka
Silmukkarakenteilla voidaan toistaa tietty koodinpätkä useita kertoja. while-silmukassa toistojen määrä riippuu totuusehdosta:
luku = 1
while luku <= 5:
# Huomaa sisennys: silmukka toistaa sisennettyä osaa!
print(luku)
luku += 1
# luku += 1 tarkoitti samaa kuin luku = luku + 1
# (ks. luku matemaattiset perusoperaattorit)
tulostaa
1 2 3 4 5
Toinen esimerkki, jossa ohjelman suoritus jatkuu silmukan jälkeen ensimmäisestä sisentämättömästä lauseesta:
# Alustetaan silmukassa tarvittavat muuttujat
luku = 1.0
lukuja = 0
while luku > 0.0:
luku = float(input("Anna luku (negatiivinen luku lopettaa):\n"))
if luku > 0.0:
lukuja += 1
# Silmukan päätyttyä suoritus jatkuu tästä
print("Annoit yhteensä", lukuja, "positiivista lukua")
Esimerkkisuoritus:
Anna luku (negatiivinen luku lopettaa):
> 324235
Anna luku (negatiivinen luku lopettaa):
> 12
Anna luku (negatiivinen luku lopettaa):
> 1
Anna luku (negatiivinen luku lopettaa):
> -1
Annoit yhteensä 3 positiivista lukua
Huom! Jos totuusehto ei täyty 1. kierroksella, while-silmukkaa ei suoriteta yhtään kertaa!
Ikuinen silmukka
while-silmukkaa käytettäessä ohjelmointivirhe voi johtaa tilanteeseen, jossa totuusehto ei koskaan muutukaan epätodeksi. Tyypillisin virhe on unohtaa silmukkalaskurin päivitys:
luku = 1
while luku <= 5:
print(luku)
# Tästä on unohtunut laskurin päivitys
# luku += 1
# Seurauksena olisi ikuinen silmukka
Ikuisesta silmukasta pääsee pois painamalla Ctrl+C (ohjelman keskeytys)
break-käsky ja "while True:" -rakenne
while-silmukasta voi poistua milloin tahansa break-käskyllä:
# Luodaan näennäisesti "ikuinen" silmukkaehto (True on aina totta)
while True:
luku = int(input("Anna kokonaisluku ja tulostan sen. Luvulla 0 lopetan: "))
if luku == 0:
print("Loppu")
# Poistutaan silmukasta break-käskyllä
break
else:
print("Annoit luvun", luku)
Esimerkkitulostus:
Anna kokonaisluku ja tulostan sen. Luvulla 0 lopetan: 6 Annoit luvun 6 Anna kokonaisluku ja tulostan sen. Luvulla 0 lopetan: 3 Annoit luvun 3 Anna kokonaisluku ja tulostan sen. Luvulla 0 lopetan: 0 Loppu
Käyttäjän syötteen testaaminen while True: -rakenteella
while True: -rakenne on hyvin hyödyllinen esimerkiksi kun ohjelman pitää lukea käyttäjän syötteitä kunnes käyttäjä antaa kelvollisen syötteen:
# Pyydetään käyttäjältä ympyrän säde ja lasketaan pinta-ala
while True:
r = float(input("Anna ympyrän säde:\n"))
if r > 0:
# Käyttäjän antama säde on OK, voidaan poistua silmukasta
break
else:
# Käyttäjä antoi virheellisen säteen, tulostetaan ilmoitus ja palataan silmukan alkuun
print("Virheellinen säde")
pinta_ala = 3.14159 * r**2
print("Pinta-ala on", round(pinta_ala, 2))
Esimerkkitulostus:
Anna ympyrän säde: > 0 Virheellinen säde Anna ympyrän säde: > -1 Virheellinen säde Anna ympyrän säde: > -2 Virheellinen säde Anna ympyrän säde: > -3 Virheellinen säde Anna ympyrän säde: > 5.8 Pinta-ala on 105.68
Toinen esimerkki:
# Pyydetään käyttäjältä kokonaislukuja ja lasketaan niiden tulo
# Merkkijono "*" lopettaa
# Alustetaan ensin tulo-muuttuja ykköseksi
tulo = 1
while True:
# Luetaan ensin käyttäjän syöte merkkijonona
teksti = input("Anna kokonaisluku. * lopettaa.\n")
if teksti == "*":
# Käyttäjä antoi tähden, poistutaan silmukasta
break
else:
# Käyttäjä antoi luvun. Muunnetaan merkkijono kokonaisluvuksi
luku = int(teksti)
# Kerrotaan tulo uudella luvulla
tulo = tulo * luku
# Tästä ohjelma palaa silmukan alkuun
print("Lukujen tulo:", tulo)
Esimerkkitulostus:
Anna kokonaisluku. * lopettaa. > 3 Anna kokonaisluku. * lopettaa. > 4 Anna kokonaisluku. * lopettaa. > 5 Anna kokonaisluku. * lopettaa. * Lukujen tulo: 60
continue- ja else-käskyt
while-silmukoissa voi lisäksi hyödyntää continue-komentoa (hyppää silmukan alkuun) ja else-lausetta (suoritetaan silmukan päätyttyä). Näitä emme hyödynnä vielä tässä vaiheessa kurssia.
Tehtävä 1.10.1
for-silmukka ja range
for-silmukassa toistojen määrä määritellään silmukan alkaessa. Toistojen määrittelyssä auttaa range-niminen funktio, jota voi käyttää kolmella eri tavalla: range(toistot), range(alku, loppu), tai range(alku, loppu, askel). Esimerkki:
# Tulostetaan Hep! viisi kertaa
# Silmukkamuuttujaa "luku" ei hyödynnetä silmukan sisällä
for luku in range(5):
print("Hep!")
tulostaa:
Hep!
Hep!
Hep!
Hep!
Hep!
Huomaa, että käytettäessä muotoa range(toistot), range-funktion silmukkalaskuri "luku" saa arvot [0 .. toistot – 1]. Eli tässä esimerkissä se saa arvot 0, 1, 2, 3 ja 4:
for luku in range(5):
print(luku * 10)
Silmukkalaskurin "luku" arvo kasvaa automaattisesti. Esimerkkikoodi tulostaa:
0 10 20 30 40
Kun range-funktion aloitusarvo määrätään käyttämällä muotoa range(alku, loppu), silmukkalaskuri "luku" saavuttaa arvon loppu – 1:
for luku in range(1, 6):
print(luku)
tulostaa
1 2 3 4 5
Silmukkalaskurin arvoa voi kasvattaa myös isommalla askeleella muodolla range(alku, loppu, askel). Nyt silmukkalaskuri "luku" saavuttaa arvon loppu – askel.
for luku in range(100, 110, 2):
print(luku)
tulostaa:
100 102 104 106 108
Arvoja voi käydä läpi myös suuremmasta pienempään. Tällöin askel on negatiivinen ja silmukkalaskuri saavuttaa arvon loppu + 1:
for luku in range(10, 5, -1):
print(luku)
tulostaa
10 9 8 7 6
Silmukan sisällä voi muokata ja hyödyntää mitä tahansa muuttujia, ei pelkästään silmukkamuuttujaa:
tilavuus = 2.0 # m^3
for kierros in range(1, 6):
print("Kierroksella", kierros, "tilavuus on", tilavuus, "m^3")
print("Kaksinkertaistetaan tilavuus...")
tilavuus = tilavuus * 2
tulostaa
Kierroksella 1 tilavuus on 2.0 m^3
Kaksinkertaistetaan tilavuus...
Kierroksella 2 tilavuus on 4.0 m^3
Kaksinkertaistetaan tilavuus...
Kierroksella 3 tilavuus on 8.0 m^3
Kaksinkertaistetaan tilavuus...
Kierroksella 4 tilavuus on 16.0 m^3
Kaksinkertaistetaan tilavuus...
Kierroksella 5 tilavuus on 32.0 m^3
Kaksinkertaistetaan tilavuus...
Sisäkkäiset silmukat
Sekä for- että while-silmukoita voi olla useampia sisäkkäin. Tässä esimerkki for-silmukalle:
for luku1 in range(1, 6):
# Käytetään print-funktiossa välilyöntiä rivinvaihdon sijasta (end = " ")
print("Luvun", luku1, "kertotaulu lukuun 10 asti:", end = " ")
for luku2 in range(1, 11):
print(luku1 * luku2, end = " ")
# Tulostetaan tyhjä merkkijono, eli pelkkä rivinvaihto
print("")
tulostaa:
Luvun 1 kertotaulu lukuun 10 asti: 1 2 3 4 5 6 7 8 9 10 Luvun 2 kertotaulu lukuun 10 asti: 2 4 6 8 10 12 14 16 18 20 Luvun 3 kertotaulu lukuun 10 asti: 3 6 9 12 15 18 21 24 27 30 Luvun 4 kertotaulu lukuun 10 asti: 4 8 12 16 20 24 28 32 36 40 Luvun 5 kertotaulu lukuun 10 asti: 5 10 15 20 25 30 35 40 45 50
Tulemme hyödyntämään for-silmukkaa huomattavan paljon enemmän kolmannesta kierroksesta eteenpäin, kun pääsemme käsittelemään Pythonin tietorakenteita kuten listoja ja sanakirjoja.
for-silmukasta poistuminen break-käskyllä.
for-silmukassa toistojen määrä kerrotaan silmukan alussa ja silmukasta ei yleensä poistuta kesken suorituksen. for-silmukasta voi kuitenkin poistua break-käskyllä samaan tapaan kuin while-silmukasta:
maksimi = int(input("Anna positiivinen kokonaisluku ja tulostan kaikki sitä pienemmät kokonaisluvut\n"))
for luku in range(1, maksimi):
print(luku)
if luku == 5:
print("En jaksa enempää")
break
tulostaa:
Anna positiivinen kokonaisluku ja tulostan kaikki sitä pienemmät kokonaisluvut
> 11
1
2
3
4
5
En jaksa enempääTehtävä 1.11.1
>
Kierros 2
Toisella kierroksella opettelemme kirjoittamaan ja käyttämään funktioita. Tutustumme mm. Python sisältämiin matemaattisiin funktioihin.
Lisäksi tutustumme moduuleihin, joiden avulla omiin ohjelmiin voi tuoda lukuisia toimintoja erilaisista ohjelmakirjastoista. Hyvä esimerkki tärkeästä moduulista on math-moduuli, joka sisältää paljon matemaattisia funktioita.
Tehtävä 2.0.1.
Funktiot
Tähän mennessä olemme jo käyttäneet muutamia Pythonin sisäänrakennettuja funktioita kuten print, input ja round:
- print-funktio tulostaa sille suluissa annetut tekstit ja muuttujat
- input-funktio tulostaa sille annetun tekstin ja palauttaa käyttäjän syöttämän merkkijonon
- round-funktio palauttaa haluttuun tarkkuuteen pyöristetyn liukuluvun
Lisäksi olemme käyttäneet funktioita tyyppimuunnoksiin:
tilavuus = float(input("Anna tilavuus:\n"))
Yllä float-funktio tekee siis tyyppimuunnoksen merkkijonosta liukuluvuksi.
Pythonissa on useita sisäänrakennettuja funktioita ja erilaiset ohjelmakirjastot sisältävät lukuisia funktioita eri käyttötarkoituksiin.
Tällä kierroksella opit kirjoittamaan omia funktioita. Niiden avulla toistuvien tehtävien suorittaminen helpottuu ja koodin rakenne pysyy selkeämpänä.
Funktioiden määritteleminen, parametrit ja paluuarvot.
Funktiolla on tavallisesti joku selkeä tehtävä, esimerkiksi tietty laskutoimitus. Funktioita kutsutaan joskus myös aliohjelmiksi.
Funktiota käytettäessä sille voidaan antaa sulkujen sisällä parametreja. Esimerkiksi funktiokutsussa
print("H2O")
parametri on merkkijono "H2O". Tässä esimerkissä taas parametreja ovat kokonaisluvut 1, 2 ja 3:
print(1, 2, 3)
Funktiolla voi olla paluuarvo. Esimerkiksi tässä esimerkissä round-funktion parametri on liukuluku 2.123 ja paluuarvo on liukuluku 2.1:
tulos = round(2.123)
Esimerkki 1
Tarkastellaan ohjelmaa, jossa luodaan funktio tuplaa ja kutsutaan sitä pääohjelmasta:
# Määritellään ensin funktio tuplaa käyttäen def-avainsanaa
# Funktio ajetaan vasta, kun sitä kutsutaan pääohjelmasta
# Huomaa, miten funktion sisältö on sisennetty
def tuplaa(luku):
return luku * 2
# Pääohjelma alkaa tästä (ei sisennystä)
# Kutsutaan funktiota "tuplaa"
iso_luku = tuplaa(12)
print(iso_luku)
- Funktio määritellään avainsanalla def, jonka jälkeen tulee funktion nimi (tuplaa)
- tuplaa-funktiolla on yksi parametri, jonka nimi on luku (suluissa funktion nimen jälkeen)
- return-avainsanan jälkeen tulee funktion paluuarvo (tässä tapauksessa parametri luku kerrottuna kahdella).
Ohjelman suoritus etenee rivi riviltä näin:
- Ensin suoritetaan pääohjelman rivi "iso_luku = tuplaa(12)". Koska rivillä kutsutaan funktiota tuplaa, ohjelman suoritus hyppää funktion sisälle. Parametrina on kokonaisluku 12.
- Funktion tuplaa ainoa rivi palauttaa parametrin luku arvon kerrottuna kahdella. Eli tässä tapauksessa 12 * 2
- return-avainsanan jälkeen suoritus jatkuu pääohjelmassa, jossa muuttuja iso_luku saa funktion paluuarvon 12 * 2, eli 24.
- Lopuksi tulostetaan kokonaisluku 24
Esimerkki 2
Tarkastellaan toista esimerkkiohjelmaa, jossa määritellään funktio tiheys ja käytetään sitä:
# Määritellään ensin funktio tiheys käyttäen def-avainsanaa
def tiheys(tilavuus, massa):
# Funktio palauttaa kappaleen tiheyden
# Funktion parametrit:
# Tilavuus: Kappaleen tilavuus (m^3)
# Massa: Kappaleen massa (kg)
# Jos funktiota kutsutaan epäfysikaalisella parametrilla, se
# tulostaa virheilmoituksen ja palauttaa arvon -1
# Tarkistetaan ensin, että parametrit ovat fysikaalisesti mielekkäät
if tilavuus <= 0:
print("Virheellinen tilavuus")
return -1
elif massa <= 0:
print("Virheellinen massa")
return -1
else:
return massa / tilavuus
# Pääohjelma alkaa tästä (ei sisennystä)
# Kysytään arvot käyttäjältä
V = float(input("Anna kappaleen tilavuus (m^3):\n"))
m = float(input("Anna kappaleen massa (kg):\n"))
# Kutsutaan tiheys-funktiota annetuilla arvoilla
rho = tiheys(V, m)
# Tarkistetaan funktion paluuarvo. -1 tarkoittaa virhettä
if rho == -1:
print("Tiheyden laskeminen epäonnistui")
else:
print("Kappaleen tiheys on:", round(rho,3), "kg/m^3")
- Tässä esimerkissä funktion tiheys suorittama laskutoimitus oli hyvin yksinkertainen.
- Oikeissa ohjelmissa funktio voi suorittaa hyvinkin monimutkaisia operaatioita. Nämä monimutkaiset operaatiot kannattaa nimenomaan "paketoida" funktioihin
- Koodin testaaminen ja virheiden etsiminen on helpompaa, kun se on jaettu funktioihin
- Hyvin kirjoitetut ja dokumentoidut funktiot ovat helposti uudelleenkäytettävissä uusissa ohjelmissa
Esimerkki 3
Tässä tapauksessa meillä on funktio kysy_suure, joka hoitaa vuorovaikutuksen käyttäjän kanssa:
# Ensin määritellään funktio. Sitä kutsutaan pääohjelmasta.
def kysy_suure(suure):
# Funktio kysyy liukulukua käyttäjältä, kunnes annettu arvo on > 0
# Parametri suure on merkkijono, esim. "massa (g)"
arvo = -1
while arvo <= 0:
arvo = float(input("Anna " + suure + ":\n"))
if arvo > 0:
return arvo
else:
print("Virheellinen arvo")
# Pääohjelma alkaa täältä
# Kysytään massa ja moolimassa funktion kysy_suure avulla
moolimassa = kysy_suure("moolimassa (g/mol)")
massa = kysy_suure("massa (g)")
n = massa / moolimassa
print("Ainemäärä on", round(n,2), "mol")
Etuna on se, että virheellisten arvojen käsittely while-silmukan avulla tarvitsee kirjoittaa vain kerran. Jos emme käyttäisi funktiota, ratkaisu voisi näyttää tältä:
# Luetaan moolimassa
arvo = -1
while arvo <= 0:
arvo = float(input("Anna moolimassa (g/mol):\n"))
if arvo > 0:
moolimassa = arvo
else:
print("Virheellinen arvo")
# Luetaan massa
arvo = -1
while arvo <= 0:
arvo = float(input("Anna massa (g):\n"))
if arvo > 0:
massa = arvo
else:
print("Virheellinen arvo")
n = massa / moolimassa
print("Ainemäärä on", round(n,2), "mol")
- Jälkimmäinen ratkaisu ei ole kovin paljon ensimmäistä pidempi, mutta kuvittele tilanne, jossa suureita pitäisi lukea kymmenen kappaletta. Tällöin funktion kysy_suure käyttäminen helpottaa koodin kirjoittamista merkittävästi.
- Jos koodiin täytyisi tehdä joku muutos, esimerkiksi vaihtaa virheilmoitus "Virheellinen arvo" joksikin muuksi, ensimmäisessä kysy_suure-funktiota käytettäessä riittää funktion kysy_suure
päivittäminen, eikä muutosta tarvitse tehdä moneen paikkaan.
Tehtävä 2.1.1
Tehtävä 2.1.2
Erilaisia funktioita
Tässä osiossa on useita esimerkkejä erilaisista funktiosta. Esimerkkejä on parasta havainnollistaa kopioimalla koodi Spyderiin ja ajamalla se itse.
1. Funktiolla ei tarvitse välttämättä olla yhtään parametria:
def pii():
# Funktio palauttaa piin arvon 15 desimaalin tarkkuudella
return 3.141592653589793
r = 1.5
pallon_tilavuus = 4 * pii() * r**3 / 3
print(round(pallon_tilavuus, 2))
2. Funktiolla voi olla useita parametreja:
def ainemaara(massa, moolimassa):
return massa / moolimassa
n = ainemaara(5.4, 18.02)
print(round(n, 3))
3. Funktiolla ei ole pakko olla paluuarvoa (return):
def tervehdys(kieli):
if kieli == "suomi":
teksti = "Hei!"
elif kieli == "ruotsi":
teksti = "Hej!"
elif kieli == "saksa":
teksti = "Hallo!"
else:
teksti = "!!??"
print(teksti)
tervehdys("suomi")
4. Funktiolla voi olla useita paluuarvoja:
def tunnit_ja_minuutit(minuutit_yhteensa):
tunnit = minuutit_yhteensa // 60 # katkaiseva jakolasku
minuutit = minuutit_yhteensa % 60 # jakojäännös
return tunnit, minuutit
luku = int(input("Anna minuuttien määrä kokonaislukuna:\n"))
h, m = tunnit_ja_minuutit(luku)
print(luku, "minuuttia on", h, "tuntia ja", m, "minuuttia")
tulostaa:
Anna minuuttien määrä kokonaislukuna:
> 124
124 minuuttia on 2 tuntia ja 4 minuuttia
5. Funktio voi sisältää useita return-käskyjä, mutta vain yksi niistä voi toteutua:
def itseisarvo(luku):
if luku >= 0:
return luku
else:
return -luku
print(itseisarvo(5.4))
print(itseisarvo(-5.4))
6. return-lause yksinkertaistaa parametrien arvojen tarkistamista
def ratkaise_p(V, n, T):
# Ratkaistaan paine ideaalikaasun tilanyhtälön avulla
# Parametrien yksiköt: V (m^3), n (mol), T(K)
# Jos joku parametreista on epäfysikaalinen,
# funktio palauttaa välittömästi arvon -1
if V <= 0 or n <= 0 or T <= 0:
return -1
# Ylläolevan if-lauseen return-käsky hoitaa virheelliset parametrit
# Jos koodi jatkaa tänne asti, tiedämme, että parametrit ovat OK
R = 8.314462618 # J K^-1 mol^-1
p = n * R * T / V
return p # Pa
print(ratkaise_p(0.25, 1.25, 300))
7. Funktiot voivat kutsua toisiaan:
def tervehdys(kieli):
if kieli == "suomi":
teksti = "Hei!"
elif kieli == "ruotsi":
teksti = "Hej!"
elif kieli == "saksa":
teksti = "Hallo!"
else:
teksti = "!!??"
print(teksti)
def keskustelu(kieli1, kieli2):
tervehdys(kieli1)
tervehdys(kieli2)
keskustelu("ruotsi", "saksa")
tulostaa:
Hej!
Hallo!
8. Valinnaiset parametrit
Funktioilla voi olla myös valinnaisia parametreja, joille on määritelty oletusarvo. Jos funktiota kutsutaan ilman valinnaista parametria, Python käyttää oletusarvoa. Tuttu esimerkki on print-funktio, jolla on useita valinnaisia parametrejä. Yksi niistä on end-parametri, jonka oletusarvo on rivinvaihto "\n". Kaksi tavallista funktiokutsuaprint("Moi!")
print("Moi!")
tulostaa
Moi!
Moi!
Kun taas vaihtamalla end-parametri tyhjäksi merkkijonoksi:
print("Moi!", end="")
print("Moi!", end="")
tulostuu
Moi!Moi!
Esimerkki valinnaisten parametrien määrittelystä:
def ratkaise_tilavuus(n, T = 273.15, p = 100000):
# Ratkaisee tilavuuden ideaalikaasun tilanyhtälöstä
# Kaikki suureet SI-yksiköissä
# Parametreillä p ja T on oletusarvot (IUPAC STP-olosuhteet)
R = 8.314462618 # J K^-1 mol^-1
V = n * R * T / p
return V
# Selvennä aina funktiota kutsuessasi, minkä valinnaisen parametrin haluat antaa
V1 = ratkaise_tilavuus(0.28) # Pelkästään pakollinen parametri n
V2 = ratkaise_tilavuus(0.28, T = 400) # n ja valinnainen parametri T
V3 = ratkaise_tilavuus(0.28, T = 300, p = 200000) # n ja molemmat valinnaiset parametrit
print(round(V1, 5), round(V2, 5), round(V3, 5))
HUOM! Valinnaiset parametrit pitää aina määritellä vasta pakollisten parametrien jälkeen. Muuten Python antaa virheilmoituksen:
SyntaxError: non-default argument follows default argument
Tehtävä 2.2.1.
Muotoiltu tulostaminen f-merkkijonoilla tai str.format-funktiolla
Tähän asti olemme käyttäneet print-funktiota tulostamiseen varsin suoraviivaisesti:
alkuaine = "C"
atomipaino = 12.011
print("Alkuaineen", alkuaine, "atomipaino on", atomipaino)
tulostaa
Alkuaineen C atomipaino on 12.011
f-merkkijonot
Pythonissa on myös edistyneempiä tapoja tulostaa muotoiltuja merkkijonoja. Pythonin versiosta 3.6 lähtien on ollut mahdollista hyödyntää ns. f-merkkijonoja (engl. f-strings), joilla muuttujien arvojen sijoittaminen merkkijonoihin on erittäin helppoa:
alkuaine = "C"
atomipaino = 12.011
# Huomaa, miten print-lausekkeen sisällä oleva merkkijono alkaa f-kirjaimella ennen lainausmerkkiä
print(f"Alkuaineen {alkuaine} atomipaino on {atomipaino}")
tulostaa
Alkuaineen C atomipaino on 12.011
f-merkkijonoja käytettäessä muuttujat voidaan siis upottaa merkkijonon sisään {muuttuja}-merkinnällä.
str.format-funktio
Ennen f-merkkijonoja muotoiltuun tulostamiseen käytettiin str.format-funktiota:
alkuaine = "C"
atomipaino = 12.011
print("Alkuaineen {} atomipaino on {}".format(alkuaine, atomipaino))
tulostaa
Alkuaineen C atomipaino on 12.011
Merkkijonon "Alkuaineen {} atomipaino on {}" kaarisulut korvautuivat siis format-funktion parametreilla alkuaine ja atomipaino. On makuasia, käyttääkö f-merkkijonoja vai str.format-funktiota. f-merkkijonoilla koodista tulee yleensä selkeämpää ja tämän kurssin oppimateriaaleissa käytetään pääasiassa f-merkkijonoja.
{}-kentän muotoilu
f-merkkijonojen {muuttuja}-kenttää voi muotoilla lukuisilla eri tavoilla. Sen tyypillisin käyttötapa on {muuttuja:<leveys>.<tarkkuus><tyyppi>}.
Kentän tyyppiä merkitään kirjaimella. Tällä kurssilla tärkeimpiä kentän tyyppejä ovat
- liukuluku f
- kokonaisluku d
- merkkijono s
Esimerkkejä:
- liukuluku pyöristettynä kolmen desimaalin tarkkuuteen, automaattinen kentän leveys: {muuttuja:.3f}
- liukuluku, 6 merkkiä leveä kenttä, pyöristettynä nollan desimaalin tarkkuuteen: {muuttuja:6.0f}
- kokonaisluku, automaattinen kentän leveys: {muuttuja:d}
- kokonaisluku, 5 merkkiä leveä kenttä: {muuttuja:5d}
- Merkkijono, automaattinen kentän leveys {muuttuja:s}
Esimerkki 1:
T = 300 # K
p = 1.12345 # atm
print(f"Olosuhteet ovat: {T:d} K, {p:.3f} atm")
tulostaa
Olosuhteet ovat: 300 K, 1.123 atm
Esimerkki 2:
n = 0.25 # mol
V = 0.00456 # m^3
T = 298.15 # K
R = 8.314462618 # J/(mol K)
p = n * R * T / V # Pa
print(f"Kun n = {n:7.3f} mol, V = {V:7.5f} m^3, T = {T:7.2f} K, on paine p = {p:7.0f} Pa")
tulostaa seitsemän merkkiä leveitä kenttiä (numerojonot 1234567 havainnollistavat kentän leveyttä)
Kun n = 0.250 mol, V = 0.00456 m^3, T = 298.15 K, on paine p = 135908 Pa
1234567 1234567 1234567 1234567
Vaikka f-merkkijonojen muotoilukenttien kokoaminen voi ensi alkuun vaikuttaa työläältä, on se todella paljon kätevämpää kuin monimutkaisten tulostusten hoitaminen
print- ja round-funktioiden avulla.
Käytä lukuarvojen tulostamiseen tästä lähtien f-merkkijonoja.
f-merkkijonojen laajempi dokumentaatio löytyy osoitteista https://docs.python.org/3/reference/lexical_analysis.html#f-strings ja https://docs.python.org/3/library/string.html#format-specification-mini-language.
Tehtävä 2.3.1.
Matemaattiset funktiot (math)
Pythonin math-niminen moduuli sisältää sisältää suuren määrän erilaisia matemaattisia funktioita ja vakioita. Moduulien luomisesta ja käyttämisestä kerrotaan lisää seuraavassa luvussa, mutta ennen kuin sukellamme syvemmälle moduulien maailmaan, otetaan math-moduulin sisältämät matemaattiset funktiot käyttöön.
math-moduuli tuodaan ensin oman ohjelman käyttöön lisäämällä ohjelman alkuun import-käsky:
import math
Tämän jälkeen moduulin sisältämiä funktioita ja vakioita voi käyttää alla olevilla tavoilla. Voit kopioida esimerkit Spyderiin ja ajaa ne, jos haluat nähdä, miten funktiot toimivat.
# exp(x) -> Eksponenttifunktio e^x print(math.exp(4)) # log(x) -> Luvun x luonnollinen logaritmi, ln(x) print(math.log(54.598150033144236)) # log(x, y) -> Luvun x logaritmi, kantaluku y print(math.log(8, 2)) # log10(x) -> Luvun x 10-kantainen logaritmi print(math.log10(10000)) # pow(x, y) -> luku x potenssiin y. Sama kuin x**y, mutta muuntaa aina luvut (ja tuloksen) liukuluvuksi print(math.pow(3, 2)) # sqrt(x) -> Luvun x neliöjuuri (kuten x**(1/2)) print(math.sqrt(9)) # pi -> pii (ei ole funktio vaan vakio) print(math.pi) # e -> Neperin luku (ei ole funktio vaan vakio) print(math.e) # sin(x), cos, tan, ... -> trigonometriset funktiot print(math.sin(math.pi / 2)) # degrees(x) -> muuntaa radiaanit asteiksi print(math.degrees(math.pi)) # radians(x) -> muuntaa asteet radiaaneiksi print(math.radians(180)) # ceil(x) -> pyöristä kokonaislukuun ylöspäin print(math.ceil(5.4)) # floor(x) -> pyöristä kokonaislukuun alaspäin print(math.floor(5.6)) # fabs(x) -> itseisarvo (muuten sama kuin Pythonin normaali abs()-funktio, mutta palauttaa aina liukuluvun) print(math.fabs(-5.6))
Math-moduulin dokumentaatio ja listaus kaikista sen sisältämistä funktioista löytyy osoitteesta https://docs.python.org/3/library/math.html
Liukulukujen yhtäsuuruuden vertailu math.isclose-funktiolla
Liukulukujen yhtäsuuruuden vertailuun ei pidä käyttää == -operaattoria vaan math.isclose-funktiota. Tällöin voit itse määritellä tarkkuuden, jolla liukulukuja verrataan. Vertailu voi olla joko suhteellinen, jolloin käytetään parametria rel_tol tai absoluuttinen, jolloin käytetään parametria abs_tol.
Otetaan ensin esimerkki, jossa suhteellinen ja absoluuttinen vertailu johtavat samaan lopputulokseen:
import math
luku1 = 2.0
luku2 = 2.005
print(f"Luvut: {luku1:.3f} ja {luku2:.3f}")
if math.isclose(luku1, luku2, rel_tol = 0.01):
print("Luvut ovat samat 1% suhteellisella tarkkuudella")
if math.isclose(luku1, luku2, abs_tol = 0.01):
print("Luvut ovat samat 0.01 absoluuttisella tarkkuudella")
tulostaa
Luvut: 2.000 ja 2.005 Luvut ovat samat 1% suhteellisella tarkkuudella Luvut ovat samat 0.01 absoluuttisella tarkkuudella
Toinen esimerkki, missä rel_tol ja abs_tol johtavat eri lopputulokseen:
import math
luku1 = 2000.0
luku2 = 2001.0
print(f"Luvut: {luku1:.3f} ja {luku2:.3f}")
if math.isclose(2000.0, 2001.0, rel_tol = 0.01):
print("Luvut ovat samat 1% suhteellisella tarkkuudella")
if not math.isclose(luku1, luku2, abs_tol = 0.01):
print("Luvut eivät ole samat 0.01 absoluuttisella tarkkuudella")
Tulostaa
Luvut: 2000.000 ja 2001.000 Luvut ovat samat 1% suhteellisella tarkkuudella Luvut eivät ole samat 0.01 absoluuttisella tarkkuudella
Valinta rel_tol ja abs_tol -parametrien välillä riippuu vertailun luonteesta. Jos esimerkiksi vertaillaan mittaustuloksia ja tiedetään vain mittausmenetelmän suhteellinen virhe, tulee käyttää suhteellista rel_tol-vertailua.
Tehtävä 2.5.1.
Moduulit
Suuremmat ohjelmakokonaisuudet on aina parasta jakaa moduuleiksi. Moduulien avulla ohjelman rakenne pysyy paremmin hallinnassa ja moduuleja voi käyttää helposti uudelleen toisissa ohjelmissa.
Käytetään esimerkkinä moduulia ideaalikaasu, joka käytännössä olisi siis alla oleva koodi tallennettuna tiedostoon ideaalikaasu.py:
# Moduuli ideaalikaasu:
# Apufunktioita ideaalikaasulle
# pV = nRT
# Moduuli määrittelee myös kaasuvakion R
# Lähde NIST CODATA2018: https://physics.nist.gov/cgi-bin/cuu/Value?r
R = 8.314462618 # J K^-1 mol^-1
# Moduuli määrittelee neljä funktiota
def ratkaise_paine(V, n, T):
return n * R * T / V
def ratkaise_tilavuus(p, n, T):
return n * R * T / p
def ratkaise_ainemaara(p, V, T):
return p * V / (R * T)
def ratkaise_lampotila(p, V, n):
return p * V / (n * R)
Luodaan moduulin ideaalikaasu.py kanssa samaan hakemistoon tiedosto testi.py, jossa hyödynnämme ideaalikaasu-moduulia import-avainsanan avulla:
# Tuodaan koko ideaalikaasu-moduuli ohjelman testi.py käyttöön
import ideaalikaasu
# ideaalikaasu-moduulin funktioiden eteen pitää lisätä viittaus "ideaalikaasu."
p = ideaalikaasu.ratkaise_paine(0.002, 0.01, 300) # Parametrit V, n, T
print(f"Paine: {p:.3f} Pa")
Tulostaa
Paine: 12471.694 Pa
Toinen tapa on tuoda ideaalikaasu-moduulista vain tietyt funktiot ja muuttujat testi.py-ohjelman käyttöön. Tähän käytetään käskyä from MODUULI import FUNKTIOT
# Tuodaan tietyt funktiot (ja/tai muuttujat) ohjelman testi.py käyttöön
from ideaalikaasu import ratkaise_paine, ratkaise_tilavuus, R
# Nyt meidän ei tarvitse käyttää "ideaalikaasu."-viittausta
p = ratkaise_paine(0.002, 0.01, 300) # Parametrit V, n, T
V = ratkaise_tilavuus(101325, 0.01, 300) # Parametrit p, n, T
print(f"Paine: {p:.3f} Pa")
print(f"Tilavuus: {V:.5f} m^3")
print(f"Kaasuvakion R arvo on {R:.8f} J/mol K")
tulostaa
Paine: 12471.694 Pa Tilavuus: 0.00025 m^3 Kaasuvakion R arvo on 8.31446262 J/mol K
Vähänkin laajemissa ohjelmakokonaisuuksissa kannattaa miettiä ohjelman pilkkomista helpommin ylläpidettäviin ja uudelleenkäytettäviin moduuleihin.
import-käskyyn voi yhdistää as-avainsanan, jolloin ohjelmaan tuotavan moduulin nimeä voi vaikkapa lyhentää. Käsky on tällöin import MODUULI as LYHENNE:
import ideaalikaasu as ik
p = ik.ratkaise_paine(0.002, 0.01, 300) # Parametrit V, n, T
Tehtävä 2.4.1.
Muuttujien näkyvyys
Tärkeää: Funktion sisällä määritellyt muuttujat, eli lokaalit muuttujat näkyvät vain kyseisessä funktiossa:
def ratkaise_p(V, n, T):
R = 8.314462618 # Lokaali muuttuja (vakio), ei näy funktion ulkopuolelle
if V > 0 and n > 0 and T > 0:
p = n * R * T / V
else:
p = 0
return p
paine = ratkaise_p(0.025, 0.30, 300)
print(f"Paine (Pa) on: {paine:.0f}")
# Tämä komento EI toimisi, koska kaasuvakio R on määritelty
# vain funktion ratkaise_p sisällä:
# print(f"Kaasuvakio (J K^-1 mol^-1) on: {R:.0f}")
Tärkeää: Funkion lokaalien muuttujien arvot "unohtuvat" samalla hetkellä kun funktiosta poistutaan! Et siis voi tallentaa lokaaleihin muuttujiin mitään pysyvää tietoa.
Lisätietoa: Globaalit muuttujat
Yleensä muuttujat kannattaa välittää funktiolle parametreina. Joskus voi silti olla tarpeen käyttää ns. globaaleja muuttujia.
Allaolevassa esimerkissä hyödynnetään globaalia muuttujaa paine. Myös ATM_TO_PA on kaikkien funktioiden käytössä, mutta se on vakio, ei muuttuja (isot kirjaimet viittaavat vakioon, jota ei tule muuttaa, ks. seuraava luku).
ATM_TO_PA = 101325 # Muuntokerroin atm -> Pa
def muuta_painetta(muutos, yksikko):
# Muutetaan globaalia muuttujaa paine funktion sisällä.
# Tällöin globaali muuttuja pitää määritellä avainsanalla global
global paine
if yksikko == 'Pa':
paine = paine + muutos
elif yksikko == 'atm':
paine = paine + muutos * ATM_TO_PA
def raportoi_paine():
# Tulostetaan paine käyttäen globaalia muuttujaa "paine"
# Huomaa, että jos globaalin muuttujan arvo halutaan vain *lukea*,
# muuttujaa ei tarvitse määritellä global-avainsanalla
print(f"Autoklaavin paine on tällä hetkellä {paine:.2f} Pa")
# Pääohjelma: alustetaan globaali muuttuja "paine" yhden ilmakehän paineeseen
paine = 1 * ATM_TO_PA
raportoi_paine()
print("Reaktio käynnistyy...")
muuta_painetta(4, 'atm') # Muuttaa globaalin muuttujan "paine" arvoa
raportoi_paine()
print("Reaktio päättyi!")
muuta_painetta(-3.8, 'atm') # Muuttaa globaalin muuttujan "paine" arvoa
raportoi_paine()
tulostaa
Autoklaavin paine on tällä hetkellä 101325.00 Pa Reaktio käynnistyy... Autoklaavin paine on tällä hetkellä 506625.00 Pa Reaktio päättyi! Autoklaavin paine on tällä hetkellä 121590.00 Pa
Huomaa, että tässä tapauksessa sama lopputulos olisi voitu saavuttaa myös funktioiden parametreja ja paluuarvoja käyttämällä:
ATM_TO_PA = 101325 # Muuntokerroin atm -> Pa
def muuta_painetta(paine, muutos, yksikko):
if yksikko == 'Pa':
return paine + muutos
elif yksikko == 'atm':
return paine + muutos * ATM_TO_PA
def raportoi_paine(paine):
print(f"Autoklaavin paine on tällä hetkellä {paine:.2f} Pa")
# Pääohjelma: alustetaan muuttuja "paine" yhden ilmakehän paineeseen
paine = 1 * ATM_TO_PA
raportoi_paine(paine)
print("Reaktio käynnistyy...")
paine = muuta_painetta(paine, 4, 'atm')
raportoi_paine(paine)
print("Reaktio päättyi!")
paine = muuta_painetta(paine, -3.8, 'atm')
raportoi_paine(paine)
Globaalien muuttujien käyttäminen voi olla perusteltua, jos se yksinkertaistaa koodia huomattavasti. global-avainsanan ajatus on, että ohjelmoijan pitää erikseen kertoa, jos hän haluaa muokata globaalia muuttujaa ja näin vältytään muokkaamasta globaalia muuttujaa vahingossa.
Tehtävä 2.6.1
Vakioiden määrittely
Usein ohjelmissa on hyvä määritellä joitain kiinteitä arvoja, jotka eivät muutu ajon aikana. Pythonissa ei ole varsinaista vakion käsitettä samaan tapaan kuin monissa muissa ohjelmointikielissä. Hyvä käytäntö on
- Nimeä vakio ISOILLA_KIRJAIMILLA
- Määrittele vakion arvo
- Älä koskaan muuta vakion arvoa sen määrittelemisen jälkeen. Jos sinun täytyy muuttaa arvoa, kyseessä ei ole vakio vaan muuttuja.
ATM_TO_PA = 101325 # Muuntokerroin atm -> Pa on vakio
p_atm = float(input("Anna paine (atm) niin muunnan sen pascaleiksi (Pa):\n"))
p_Pa = p_atm * ATM_TO_PA
print(f"{p_atm:.3f} atm on {p_Pa:.0f} Pa")tulostaa
Anna paine (atm) niin muunnan sen pascaleiksi (Pa):
0.454
0.454 atm on 46002 PaKun muuntokerroin on määritelty vakiona yhdessä paikassa, pienenee myös inhimillisten virheiden määrä. Näin muuntokertoimelle ei tule vahingossa käytettyä eri arvoa eri paikoissa. Jos olet kirjoittamassa laajempaa ohjelmaa, jossa käytetään useita luonnonvakioita, on yleensä hyvä ratkaisu määritellä kaikki luonnonvakiot omassa moduulissaan (esim. luonnonvakiot.py) ja ottaa tämä moduuli käyttöön tarpeen mukaan.
Kierros 3
Kolmannella kierroksella opettelemme käyttämään erilaisia tietorakenteita. Tutustumme mm. listoihin, monikkoihin ja sanakirjoihin. Tietorakenteiden avulla suuretkin datamäärät pysyvät hyvin järjestyksessä.
Tehtävä 3.0.1.
Pythonin tietorakenteita
Tähän mennessä olemme tutustuneet yksinkertaisiin tietotyyppeihin kuten int, float, str ja bool. Nämä tietotyypit ovat yksinkertaisia, koska niihin tallennetaan käytännössä vain yksi arvo, kuten yksi kokonaisluku. Mutta entä
jos haluaisimme säilöä vaikka 1000 kokonaislukua? Emme varmaankaan haluaisi määritellä tuhatta muuttujaa?
Otetaan nyt käyttöön monimutkaisempia tietorakenteita, joiden avulla voi hallita suuria tietomääriä. Pythonissa on useita erilaisia tietorakenteita eri käyttötarkoituksiin. Tietorakenteet esitellään lyhyesti alla ja niistä kerrotaan enemmän seuraavissa kappaleissa.
Lista
lista (list) on erittäin joustava tietorakenne. Listat määritellään hakasulkeiden avulla:
tilavuudet = [10.2, 2.6, 3.55]
Listan yksittäistä arvoa kutsutaan listan alkioksi. Ylläolevassa listassa on siis kolme alkiota.
Monikko
monikko (tuple) on kuten lista, mutta sitä ei voi muokata. Monikot määritellään tavallisten sulkeiden avulla:
jalokaasut = ('He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn')
Kuten listojen kohdalla, myös monikon yksittäinen arvo on monikon alkio. Ylläolevassa listassa on siis kuusi alkiota.
Sanakirja
sanakirja (dictionary) koostuu avain:arvo -pareista. Avainten tulee olla uniikkeja. Sanakirjat määritellään kaarisulkeiden avulla:
atomipainot = {'H': 1.008, 'C': 12.011, 'O': 15.999}
Yllä olevassa sanakirjassa on siis kolme avain:arvo -paria.
Joukko
joukko (set) on tietorakenne, jossa kukin arvo voi esiintyä vain kerran. Emme hyödynnä joukkoja tällä kurssilla. Joukot määritellään kaarisulkeilla, mutta toisin kuin sanakirjat, joukot koostuvat yksittäisistä arvoista ilman avaimia:
metallit = {'Cu', 'Ag', 'Cu', 'Ag'}
Ylläolevan määrittelyn jälkeen metallit-joukon sisältö on {'Cu', 'Ag'}, eli vain uniikit arvot on tallennettu joukkoon.
Tehtävä 3.1.1.
Listat
Yhtä tietotyyppiä sisältävät listat
Alla on esimerkkejä yksinkertaisista listoista (list), joissa on pelkästään yhden tyyppisiä arvoja:
# Kokonaislukuja sisältävä lista, viisi alkiota kokonaisluvut = [5, 6, 7, 8, 9] # Liukulukuja sisältävä lista, kolme alkiota liukuluvut = [0.3, 0.33333, 355.555] # Merkkijonoja sisältävä lista, neljä alkiota merkkijonot = ["Kupari", "Hopea", "Kulta", "Roentgenium"] # Tyhjä lista (pelkät hakasulkeet) vakuumi = []
Listan pituus
Listan pituuden voi selvittää len-funktiolla:
jalokaasut = ["He", "Ne", "Ar", "Kr", "Xe", "Rn"]
print(f"Jalokaasut: {jalokaasut}")
print(f"Jalokaasujen määrä: {len(jalokaasut)}")
tulostaa
Jalokaasut: ['He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn'] Jalokaasujen määrä: 6
Huomaa, että kun Python tulostaa merkkijonoja sisältävän listan, se käyttää yksinkertaisia lainausmerkkejä ('He'). Tämä on aivan sama kuin "He". Alla olevissa esimerkeissä käytetään listaa määritellessä yksinkertaisia lainausmerkkejä.
Listojen indeksointi
Listan alkioilla on indeksi, jolla niihin voi viitata. Huom! Indeksointi alkaa nollasta.
jalokaasut = ['He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn'] # indeksi: 0 1 2 3 4 5 print(jalokaasut[0]) print(jalokaasut[3])
tulostaa:
He
Kr
Alkioihin voi viitata myös negatiivisella indeksillä. Tällöin viimeisen alkion indeksi on -1. Negatiivisen indeksoinnin etuja on mm. se, ettei tarvitse käyttää len-funktiota viimeisen alkion osoittamiseksi:
jalokaasut = ['He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn'] # neg. indeksi: -6 -5 -4 -3 -2 -1 print(jalokaasut[-1]) # Palauttaa viimeisen alkion print(jalokaasut[-2]) # Palauttaa toiseksi viimeisen alkion print(jalokaasut[len(jalokaasut) - 1]) # Toinen tapa palauttaa viimeinen alkio
tulostaa
Rn
Xe
Rn
Listojen siivuttaminen
Listasta voi valita useita alkoita kerralla, jolloin tulos on uusi lista. Tätä kutsutaan listan siivuttamiseksi (engl. slicing)
lista[alku:loppu] # indeksistä alku indeksiin loppu-1 lista[alku:] # indeksistä alku alkaen listan loppuun asti lista[:loppu] # listan alusta indeksiin loppu-1 asti lista[alku:loppu:askel] # indeksistä alku indeksiin loppu-1, käyttäen askelväliä askel lista[:] # Kopio listan kaikista alkioista
eli käytännön esimerkit:
jalokaasut = ['He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn'] # indeksi: 0 1 2 3 4 5 print(jalokaasut[2:4]) # uusi lista ['Ar', 'Kr'] print(jalokaasut[:3]) # uusi lista ['He', 'Ne', 'Ar'] print(jalokaasut[3:]) # uusi lista ['Kr', 'Xe', 'Rn'] print(jalokaasut[-2:]) # uusi lista ['Xe', 'Rn'], eli kaksi viimeistä alkiota print(jalokaasut[0:6:2]) # uusi lista ['He', 'Ar', 'Xe'] # Viimeisessä esimerkissä poimitaan siis joka toinen alkio käyttämällä askelta 2
Listan täyttäminen range-funktion avulla
for-silmukoiden yhteydessä tutustuimme range-funktioon, jolla voi luoda numerosarjoja. range-funktion avulla voi myös täyttää listoja:
parilliset = list(range(2, 11, 2)) kymmenet = list(range(10, 101, 10)) print(parilliset) print(kymmenet)
tulostaa
[2, 4, 6, 8, 10] [10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
Useita tietotyyppejä sisältävät listat
Lista on erittäin monipuolinen tietorakenne ja yksi lista voi sisältää useampia tietotyyppejä:
yhdiste = ['C', 2, 'H', 6, 'O', 1] # str ja int luvut = [0, 0.5, 1, 1.5, 2, 2.5, 3] # int ja float
Lista funktion parametrina
Listoja voi käyttää funktioiden parametreina aivan kuten aiemmin olemme käyttäneet esimerkiksi kokonaislukuja ja merkkijonoja. Määritellään funktio joka_toinen_alkio, joka saa parametrina listan ja palauttaa uuden listan, jossa on alkuperäisen listan joka toinen alkio:
# Funktion määrittely
def joka_toinen_alkio(lista):
# Siivuteteaan listasta joka toinen alkio
uusi_lista = lista[0::2]
return uusi_lista
# Pääohjelma
numerot = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
numerot2 = joka_toinen_alkio(numerot)
print(numerot2)
tulostaa
[1, 3, 5, 7, 9]
Syventävää tietoa: listan "purkaminen" funktion parametreiksi
Joillekin funktiolle voi antaa listan "puretussa" muodossa (unpacking). Tällöin parametrina annettavan listan nimen eteen lisätään *-merkki:
jalokaasut = ['He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn']
print(jalokaasut)
print(*jalokaasut)
# Jälkimmäinen on sama asia kuin
# print('He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn')
tulostaa
['He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn'] He Ne Ar Kr Xe Rn
Ensimmäisessä tapauksessa jalokaasut-lista välittyi print-funktiolle listana ja sellaisena se myös tulostui. Jälkimmäisessä tapauksessa lista "purettiin" kuudeksi erilliseksi parametriksi ja print-funktio tulosti nämä parametrit välilyönnillä erotettuina.
Syventävää tietoa: listan kopioiminen
Edellä mainittiin komento lista[:], jolla voi luoda kopion listasta. Käytännön esimerkki, jossa luodaan kopio listasta ja kopion muokkaaminen ei vaikuta alkuperäiseen listaan:
jalokaasut = ['He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn'] # indeksi: 0 1 2 3 4 5 jalokaasut_kopio = jalokaasut[:] print(jalokaasut_kopio[1]) # Tulostaa Ne jalokaasut_kopio[1] = "Neon" print(jalokaasut_kopio[1]) # Tulostaa Neon print(jalokaasut[1]) # Tulostaa Ne
Listojen kanssa yksinkertainen sijoitus jalokaasut2 = jalokaasut ei enää toimikaan samalla tavalla kuin yksinkertaisten tietotyyppien (kuten int) kanssa. Komennon jälkeen lista jalokaasut2 viittaa alkuperäiseen listaan jalokaasut ja listan jalokaasut2 muokkaaminen muokkaa myös alkuperäistä listaa jalokaasut:
jalokaasut_viittaus = jalokaasut print(jalokaasut_viittaus[1]) # Tulostaa Ne jalokaasut_viittaus[1] = "Neon" print(jalokaasut_viittaus[1]) # Tulostaa Neon print(jalokaasut[1]) # Tulostaa Neon
Tähän toimintatapaan on omat järkevät syynsä, kuten muistin säästäminen. Tämän kurssin puitteissa emme käsittele ylläolevan kaltaisia viittauksia tietorakenteisiin, vaan meille riittää listojen sisällön kopioiminen. Tämä asia on kuitenkin hyvä painaa mieleen, koska viitteiden käyttäminen vahingossa on helppo tapa ns. ampua itseään jalkaan.
Tehtävä 3.2.1
Listojen käsittely
Listoja voi muokata useilla erilaisilla funktiolla:
Alkioiden lisääminen
# Tyhjä lista luodaan pelkillä hakasulkeilla
alkuaineet = []
# 1) append-funktio lisää listaan yhden alkion:
alkuaineet.append('Cu')
alkuaineet.append('Ag')
# alkuaineet on nyt ['Cu', 'Ag']
# 2) Listoja voi yhdistää "+"-operaattorilla:
alkuaineet = alkuaineet + ['S', 'O']
# alkuaineet on nyt ['Cu', 'Ag', 'S', 'O']
# 3) extend-funktio lisää useita alkioita listan loppuun:
alkuaineet.extend(['Hg', 'Au'])
# alkuaineet on nyt ['Cu', 'Ag', 'S', 'O', 'Hg', 'Au']
# 4) insert-funktio lisää alkion haluttuun kohtaan:
alkuaineet.insert(0, 'Na')
# alkuaineet on nyt ['Na', 'Cu', 'Ag', 'S', 'O', 'Hg', 'Au']
Alkioiden poistaminen
# remove(x) poistaa alkion, jonka arvo on x
alkuaineet = ['Na', 'Cu', 'Ag', 'S', 'O', 'Hg', 'Au']
alkuaineet.remove('Au')
# alkuaineet on nyt ['Na', 'Cu', 'Ag', 'S', 'O', 'Hg']
# del-komento poistaa alkion, jonka indeksi on n
del alkuaineet[0]
# alkuaineet on nyt ['Cu', 'Ag', 'S', 'O', 'Hg']
Alkion olemassaolon testaaminen ja indeksin etsiminen
# in-avainsanalla voi testata, onko alkio listassa:
alkuaineet = ['Cu', 'Ag', 'S', 'O', 'Hg']
if 'O' in alkuaineet:
print("Happi on vahvasti mukana")
# in-avainsanasta on myös käänteisversio "not in":
if 'He' not in alkuaineet:
print("Ei ole heliumia")
# index-funktio kertoo tietyn alkion indeksin
print(f"Kuparin indeksi listassa on: {alkuaineet.index('Cu')}")
tulostaa
Happi on vahvasti mukana Ei ole heliumia Kuparin indeksi listassa on: 1
Listojen lajittelu
# Listan lajittelu (aakkosjärjestykseen) sort-funktiolla alkuaineet = ['Cu', 'Ag', 'S', 'O', 'Hg'] alkuaineet.sort() # alkuaineet on nyt ['Ag', 'Cu', 'Hg', 'O', 'S']
Listan pienin ja suurin alkio
Listan pienimmän alkion voi etsiä min-funktiolla ja suurimman alkion max-funktiolla:
aallonpituudet = [532, 632, 588, 229, 1030, 601]
print(min(aallonpituudet))
print(max(aallonpituudet))
tulostaa
229
1030
Tehtävä 3.3.1.
Listojen läpikäynti (for, zip)
Listan läpikäyminen for-silmukan avulla
Kun meillä on tietoja tallennettuna listaan, haluamme yleensä myös hyödyntää niitä. Tätä varten tarvitsemme menetelmän listojen läpikäyntiin. Seuraava tapa ei olisi kovin kätevä, jos listassa olisi tuhat alkiota:
# Muuntokerroin atm -> bar ATM_TO_BAR = 1.01325 # Määritellään kolme painetta yksiköissä atm paineet_atm = [0.56, 1.22, 2.34] # indeksi: 0 1 2 # Muunnetaan paineet bareiksi suoraviivaisesti alkio kerrallaan ja tulostetaan ne print(round(paineet_atm[0] * ATM_TO_BAR, 3)) print(round(paineet_atm[1] * ATM_TO_BAR, 3)) print(round(paineet_atm[2] * ATM_TO_BAR, 3))
Luonnollisin tapa listojen läpikäyntiin on for-silmukka (johon tutustuimme 1. kierroksella). Listojen kanssa pääsemme toden teolla hyödyntämään for-silmukoita.
Esimerkki 1
# Muuntokerroin atm -> bar
ATM_TO_BAR = 1.01325
# Määritellään kolme painetta yksiköissä atm:
paineet_atm = [0.56, 1.22, 2.34]
# indeksi: 0 1 2
# Tulostetaan paineet bareina yksi kerrallaan for-silmukan avulla
for paine_atm in paineet_atm:
paine_bar = paine_atm * ATM_TO_BAR
print(f"Paine: {paine_bar:.3f} Pa")
tulostaa
Paine: 0.567 Pa Paine: 1.236 Pa Paine: 2.371 Pa
Näin for-silmukan avulla voi käydä läpi helposti listan kaikki alkiot, on niitä sitten kolme tai 3000. Listan läpikäyvän for-silmukan yleinen muoto on siis:
for ALKIO in LISTA:
print(ALKIO) # silmukassa voimme tehdä alkiolla mitä haluamme
Esimerkki 2
Toteutetaan funktio joka tulostaa kaikki listan kymmenellä jaolliset luvut:
def tulosta_kymmenet(luvut):
# Funktio saa listan kokonaislukuja, jotka ovat pienempiä kuin 100
# Funktio tulostaa kaikki kymmenellä jaolliset luvut
# Funktion paluuarvo on tulostettujen lukujen määrä
tulostetut = 0
for luku in luvut:
if luku % 10 == 0:
print(luku)
tulostetut += 1
return tulostetut
tulosta_kymmenet([4, 3, 20, 60, 99])
tulostaa:
20
60
Esimerkki 3
Käydään läpi yhtä listaa ja lisätään samalla alkioita toiseen listaan append-funktiolla:
# Ratkaistaan paine ideaalikaasun tilanyhtälöstä usealle eri tilavuudelle
n = 0.5 # mol
T = 298.15 # K
R = 8.314462618 # J K^-1 mol^-1
# Määritellään kolme tilavuutta yksiköissä m^3
tilavuudet = [0.010, 0.045, 0.105]
# Luodaan tyhjä lista laskettavia paineita varten
paineet = []
# Lasketaan paineet yksiköissä Pa
for tilavuus in tilavuudet:
paine = n * R * T / tilavuus
paineet.append(paine)
# Tulostetaan tilavuudet ja paineet yksinkertaisesti ilman pyöristystä
print(f"tilavuudet: {tilavuudet}")
print(f"paineet: {paineet}")
tulostaa
tilavuudet: [0.01, 0.045, 0.105]
paineet: [123947.85147783499, 27543.966995074446, 11804.557283603333]
Esimerkki 4
Tulostetaan tietoja kahdesta yhtä pitkästä listasta.
Tehdään suoraviivainen for-silmukka, jossa hyödynnetään silmukkamuuttujaa i.
tilavuudet = [0.01, 0.045, 0.105]
paineet = [123947.80946849998, 27543.957659666663, 11804.553282714285]
# Hyödynnetään silmukkamuuttujaa i ja len-funktiota.
# Silmukkamuuttuja i saa siis arvot range(len(paineet)), eli [0, 1, 2]
for i in range(len(paineet)):
print(f"V = {tilavuudet[i]:.3f} m^3; p = {paineet[i]:.0f} Pa")
tulostaa
V = 0.010 m^3; p = 123948 Pa
V = 0.045 m^3; p = 27544 Pa
V = 0.105 m^3; p = 11805 Pa
Esimerkki 5
Lasketaan arvoja kolmanteen listaan kahden keskenään yhtä pitkän listan avulla:
ainemaarat = [0.4, 0.6, 0.8] # mol
tilavuudet = [0.25, 0.25, 0.25] # l
konsentraatiot = [] # Lasketaan konsentraatiot (mol/l)
for i in range(len(ainemaarat)):
c = ainemaarat[i] / tilavuudet[i]
konsentraatiot.append(c)
print(konsentraatiot)
tulostaa
[1.6, 2.4, 3.2]
Yllä olevilla suoraviivaisilla for-silmukoilla kurssin tehtävistä selviää täysin hyväksyttävästi. Alla esitellään vielä zip- ja enumerate-funktiot, joilla yllä olevan kaltaiset silmukat on yleensä helpompi toteuttaa.
zip-funktio
Kätevä tapa hoitaa esimerkin 5 tilanne on yhdistää kaksi listaa zip-funktion avulla (engl. zip = vetoketju):
ainemaarat = [0.4, 0.6, 0.8] # mol
tilavuudet = [0.25, 0.25, 0.25] # l
konsentraatiot = [] # Lasketaan konsentraatiot (mol/l)
for n, V in zip(ainemaarat, tilavuudet):
# silmukkamuuttuja n saa arvot listasta ainemaarat
# silmukkamuuttuja V saa arvot istasta tilavuudet
c = n / V
konsentraatiot.append(c)
print(konsentraatiot)
Lopputulos olisi sama kuin edellä. Katsotaan tarkemmin, mitä zip-funktio palauttaa (muuntamalla funktion tulos listaksi):
print(list(zip(ainemaarat, tilavuudet)))
tulostaa
[(0.4, 0.25), (0.6, 0.25), (0.8, 0.25)]
Eli kolmen alkion lista, jossa jokainen alkio on kahden alkion monikko (lista, jota ei voi muokata).
zip-funktio on erittäin kätevä tapa yhdistää listoja for-silmukkaa varten.
enumerate-funktio.
enumerate-funktio on myös usein avuksi listojen läpikäymisessä. Se palauttaa kullekin listan alkiolle sekä sen indeksin että alkion arvon:
alkuaineet = ["H", "He", "Li", "Be"]
for indeksi, alkuaine in enumerate(alkuaineet):
print(f"Z: {(indeksi + 1):d}; alkuaine: {alkuaine:s}")
tulostaa
Z: 1; alkuaine: H
Z: 2; alkuaine: He
Z: 3; alkuaine: Li
Z: 4; alkuaine: Be
Saman silmukan voisi toteuttaa myös yksinkertaisen silmukkamuuttujan avulla:
alkuaineet = ["H", "He", "Li", "Be"]
for i in range(len(alkuaineet)):
print(f"Z: {(i + 1):d}; alkuaine: {alkuaineet[i]:s}")
On lähinnä makuasia, kumpaa tapaa käyttää. enumerate-funktio voi auttaa tekemään koodista luettavampaa kuin silmukkamuuttujan käyttö.
Katsotaan vielä tarkemmin, mitä enumerate-funktio oikeastaan palauttaa (muunnetaan enumerate-funktion tulos listaksi):
alkuaineet = ["H", "He", "Li", "Be"]
print(list(enumerate(alkuaineet)))
tulostaa
[(0, 'H'), (1, 'He'), (2, 'Li'), (3, 'Be')]
Eli kukin alkuaineet-listan alkio on saanut parikseen indeksin. Tässä listassa on neljä alkiota ja jokainen alkio on kahden alkion monikko.
Lisätietoa: List comprehension -mekanismi
(Tämä kappale on syventävää tietoa, ei välttämätöntä kurssin läpäisemiseksi).
Kuten ylläolevat esimerkit näyttää, for -silmukka on selkeä työkalu listojen läpikäymiseen ja uusien listojen luomiseen. Mainitsen tässä syventävänä tietona myös List comprehension -mekanismin, jolla Pythonissa on erityisen kätevää luoda uusia listoja olemassaolevien listojen avulla.
List comprehension-lauseke kirjoitetaan hakasulkeiden väliin:
uusi_lista = [ uuden_listan_alkion_lauseke for vanha_alkio in vanha_lista ]
Esimerkki:
tilavuudet_m3 = [0.010, 0.045, 0.105] tilavuudet_litroina = [ tilavuus_m3 * 1000 for tilavuus_m3 in tilavuudet_m3 ] print(tilavuudet_m3) print(tilavuudet_litroina)
tulostaa
[0.01, 0.045, 0.105]
[10.0, 45.0, 105.0]Toinen esimerkki:
# Ratkaistaan paine ideaalikaasun tilanyhtälöstä usealle eri tilavuudelle n = 0.5 # mol T = 298.15 # K R = 8.314462618 # J K^-1 mol^-1 # Määritellään kolme tilavuutta yksiköissä m^3 tilavuudet = [0.010, 0.045, 0.105] # Käytetään for-silmukan sijasta "List comprehension"-mekanismia paineet = [ n * R * T / tilavuus for tilavuus in tilavuudet ] # Tulostetaan tilavuudet ja paineet yksinkertaisesti ilman pyöristystä print("tilavuudet:", tilavuudet) print("paineet:", paineet)
tulostaa
tilavuudet: [0.01, 0.045, 0.105] paineet: [123947.85147783499, 27543.966995074446, 11804.557283603333]
Tehtävä 3.4.1.
Monikot
Emme käytä paljon aikaa monikkojen käsittelyyn, sillä tämän kurssin puitteissa meille riittää tieto, että monikko on muuten kuin lista, mutta sitä ei voi muokata:
# Monikko määritellään siis tavallisilla sulkeilla
jalokaasut = ("He", "Ne", "Ar", "Kr", "Xe", "Rn")
# indeksi 0 1 2 3 4 5
# Monikon alkioihin viitataan hakasulkeilla
print(jalokaasut[2]) # Tulostaa Ar
# Seuraavat komennot ovat virheellisiä monikkojen tapauksessa
jalokaasut[2] = "H"
# TypeError: 'tuple' object does not support item assignment
del jalokaasut[0]
# TypeError: 'tuple' object doesn't support item deletion
Törmäämme monikkoihin lähinnä tilanteissa, joissa Python käyttää sisäisesti monikkoa tyyppinä. Esimerkiksi edellisessä kappaleessa esitelty zip-funktio tuottaa monikoita:
alkuaineet = ['H', 'C', 'O'] atomipainot = [1.008, 12.011, 15.999] alkuaine_monikot = zip(alkuaineet, atomipainot) print(list(alkuaine_monikot))
tulostaa
[('H', 1.008), ('C', 12.011), ('O', 15.999)]
Eli lista, jossa on kolme alkiota, joista jokainen on kahden alkion monikko. Käytännön esimerkki zip-funktion hyödyntämisestä tässä tapauksessa:
alkuaineet = ['H', 'C', 'O']
atomipainot = [1.008, 12.011, 15.999]
for alkuaine, atomipaino in zip(alkuaineet, atomipainot):
print(f"Alkuaineen {alkuaine:s} atomipaino on {atomipaino:.3f} g/mol")
tulostaa
Alkuaineen H atomipaino on 1.008 g/mol Alkuaineen C atomipaino on 12.011 g/mol Alkuaineen O atomipaino on 15.999 g/mol
Saman asian voisi hoitaa silmukkamuuttujaa käyttävällä for-silmukalla, mutta zip-funktio on tavallaan "luonnollisempi" tapa hoitaa asia Pythonissa.
Tehtävä 3.5.1.
Sanakirjat
Sanakirjassa alkiot määritellään avain:arvo -pareina:
atomipainot = {"H": 1.008, "C": 12.011, "O": 15.999}
Tämän määrittelyn jälkeen avainta vastaavan arvon voi noutaa näin:
print("Hiilen atomipaino on", atomipainot["C"])
tulostaa
Hiilen atomipaino on 12.011
Määrittelyssä käytetään siis kaarisulkeita, mutta kun arvoihin viitataan avaimella, käytetään hakasulkeita.
Tyhjän sanakirjan luominen
uusi_sanakirja = {}
Arvojen lisääminen sanakirjaan
Arvojen lisääminen sanakirjaan on helppoa: annetaan vain uusi avain ja arvo:
# Luodaan tyhjä sanakirja ja lisätään kolme avain:arvo -paria atomipainot = {} atomipainot["H"] = 1.008 atomipainot["C"] = 12.011 atomipainot["O"] = 15.999 print(atomipainot)
Tulostaa
{'H': 1.008, 'C': 12.011, 'O': 15.999}
Sanakirjan voi myös määritellä ensin tiettyjen avain:arvo parien kanssa ja lisätä siihen myöhemmin lisää pareja:
atomipainot = {"H": 1.008, "C": 12.011, "O": 15.999}
atomipainot["P"] = 30.973
print(atomipainot)
tulostaa
{'H': 1.008, 'C': 12.011, 'O': 15.999, 'P': 30.973}
Python tulostaa sanakirjojen avaimet aina yksinkertaisia lainausmerkkejä käyttäen.
Arvon lisääminen sanakirjaan muuttujan avulla
Arvoja voi lisätä sanakirjaan myös käyttämällä avaimena olemassa olevan muuttujan sisältöä:
atomipainot = {"H": 1.008, "C": 12.011, "O": 15.999}
# Kysytään käyttäjältä uusi alkuaine ja atomipaino sanakirjaan
alkuaine = input("Anna alkuainesymboli\n")
atomipaino = float(input("Anna atomipaino\n"))
# alkuaine on nyt merkkijonomuuttuja, esimerkiksi "P"
# atomipaino on nyt liukuluku, esimerkiksi 30.973
atomipainot[alkuaine] = atomipaino
# Tulostetaan sanakirjan sisältö
print("Atomipainot:", atomipainot)
Esimerkkiajo:
Anna alkuainesymboli > P Anna atomipaino > 30.973 Atomipainot: {'H': 1.008, 'C': 12.011, 'O': 15.999, 'P': 30.973}
Kurssin aikana käytämme lukuisia kertoja merkintää sanakirja[muuttuja] = arvo, kun haluamme lisätä avain:arvo-pareja sanakirjaan.
Arvon poimiminen sanakirjasta muuttujan avulla
Arvoja voi poimia sanakirjasta myös käyttämällä avaimena olemassa olevan muuttujan sisältöä:
atomipainot = {"H": 1.008, "C": 12.011, "O": 15.999}
# Kysytään käyttäjältä alkuaine
alkuaine = input("Anna alkuainesymboli, niin tulostan atomipainon:\n")
# alkuaine on nyt merkkijonomuuttuja, esimerkiksi "C"
print(atomipainot[alkuaine])
Esimerkkiajo:
Anna alkuainesymboli, niin tulostan atomipainon: > C 12.011
Kurssin aikana käytämme lukuisia kertoja merkintää arvo = sanakirja[muuttuja], kun haluamme poimia tietyn arvon sanakirjasta.
Arvojen poistaminen sanakirjasta
Arvojen poistaminen sanakirjasta onnistuu del-avainsanalla:
atomipainot = {"H": 1.008, "C": 12.011, "O": 15.999}
del atomipainot["C"]
print(atomipainot)
tulostaa
{'H': 1.008, 'O': 15.999}
Avaimen olemassaolon tarkistaminen sanakirjasta
in-avainsana toimii samaan tapaan kuin listojen kanssa:
# in-avainsanalla voi testata, onko avain sanakirjassa:
atomipainot = {"H": 1.008, "C": 12.011, "O": 15.999}
if "C" in atomipainot:
print("Hiilen atomipaino on", atomipainot["C"])
tulostaa
Hiilen atomipaino on 12.011
Sanakirjan läpikäyminen, items()
Sanakirjan items()-funktio antaa arvot läpikäyntiä varten:
atomipainot = {"H": 1.008, "C": 12.011, "O": 15.999}
for alkuaine, atomipaino in atomipainot.items():
print(f"Alkuaineen {alkuaine:s} atomipaino on {atomipaino:.3f} g/mol")
tulostaa
Alkuaineen H atomipaino on 1.008 g/mol Alkuaineen C atomipaino on 12.011 g/mol Alkuaineen O atomipaino on 15.999 g/mol
Yleinen muoto siis
for AVAIN, ARVO in SANAKIRJA.items():
print(AVAIN, ARVO) # Silmukassa voimme käyttää avaimia ja arvoja kuten haluamme.
Sanakirjan lajitteleminen
sorted()-funktiolla voi tulostaa avaimet aakkosjärjestyksessä tai arvot järjestyksessä (sanakirjan values-funktio):
atomipainot = {"P": 30.973, "C": 12.011, "O": 15.999}
print(sorted(atomipainot))
print(sorted(atomipainot.values()))
tulostaa
['C', 'O', 'P'] [12.011, 15.999, 30.973]
Huomaa kuitenkin, että alkuperäisen sanakirjan (atomipainot) järjestys ei muutu, vaikka kutsuisit sorted-funktiota.
Huom! Ennen Pythonin versiota 3.6, sanakirjan avain:arvo parit olivat satunnaisessa järjestyksessä. Versiosta 3.6 eteenpäin ne ovat siinä järjestyksessä, missä ne on lisätty sanakirjaan.
Listat sanakirjojen sisällä
Sanakirjan arvot voivat olla vaikka listoja:
# Sanakirjan arvot voivat olla vaikka listoja:
yhdisteet = {"C2H6": ["C", 2, "H", 6],
"NaCl": ["Na", 1, "Cl", 1]
# indeksi: 0 1 2 3
}
print(yhdisteet["C2H6"])
print("Yhdisteessa C2H6 on", yhdisteet["C2H6"][3], "vetyatomia")
tulostaa
['C', 2, 'H', 6]
Yhdisteessa C2H6 on 6 vetyatomiaTehtävä 3.6.1
Sisäkkäiset tietorakenteet
Pythonin erilaisia tietorakenteita voi käyttää myös sisäkkäin. Jos listoja sisältävä lista kuulostaa erikoiselta, suosittelen vahvasti kokeilemaan allaolevia esimerkkejä Spyderissä ja kokeilemaan niiden muokkausta.
Sisäkkäiset listat
Listan alkio voi olla myös toinen lista:
# Määritellään lista, jossa kaksi alkiota. Kukin alkio on kolmen alkion lista. lista = [[10, 20, 30], [1, 2, 3]] print(lista[0][0]) print(lista[1][2])
tulostaa
10
3
Eli merkinnässä lista[1][2] ensimmäinen indeksi [1] viittaa ulomman listan toiseen alkioon [1, 2, 3] (indeksointi alkaa nollasta!). Toinen indeksi [2] viittaa sisemmän listan kolmanteen alkioon (indeksointi alkaa nollasta!).
Otetaan käytännöllisempi esimerkki. Kuvataan kemiallista yhdistettä listalla:
- Listan jokainen alkio on toinen lista
- Tämä lista sisältää alkuaineen symbolin ja sen määrän yhdisteessä
yhdiste_1 = [['C', 2], ['H', 6]] yhdiste_2 = [['Ca', 1], ['Cl', 2]] # Lisätään nyt kaikki yhdisteet yhteen listaan ja tulostetaan yhdisteet = [yhdiste_1, yhdiste_2] print(yhdisteet)
tulostaa
[[['C', 2], ['H', 6]], [['Ca', 1], ['Cl', 2]]]
Laajempi esimerkki
# Käydään läpi yhdisteet, tulostetaan ne ja etsitään hiilivedyt
yhdisteet = [[['C', 2], ['H', 6]], [['Ca', 1], ['Cl', 2]]]
for yhdiste in yhdisteet:
# "yhdiste" on nyt esim. [['C', 2], ['H', 6]]
# Alustetaan muuttujat ennen sisempää for-silmukkaa
yhdisteen_kaava = ""
on_hiili = on_vety = False
# Käydään läpi kaikki yhdisteen alkuaineet
for alkuaine in yhdiste:
# "alkuaine" on nyt esim. ['C', 2]
# Tulostetaan määrä vain, jos se on > 1
if alkuaine[1] > 1:
maara = str(alkuaine[1])
else:
maara = ""
yhdisteen_kaava += alkuaine[0] + maara
# Tarkistetaan, onko alkuaine hiili tai vety
if alkuaine[0] == 'C':
on_hiili = True
elif alkuaine[0] == 'H':
on_vety = True
# Tulostetaan yhdisteen molekyylikaava
if len(yhdiste) == 2 and on_hiili and on_vety:
hiilivety_str = "on hiilivety"
else:
hiilivety_str = ""
print("Yhdiste:", yhdisteen_kaava, hiilivety_str)
tulostaa
Yhdiste: C2H6 on hiilivety Yhdiste: CaCl2
Matriisit listojen avulla
Sisäkkäisillä listoilla voisi periaatteessa kuvata matriiseja:
matriisi = [[2, 4],
[5, 6]]
# Tulostetaan 1. rivin 2. alkio (indeksointi nollasta!)
print(matriisi[0][1]) # tulostaa 4
Käytännössä matriisilaskentaan käytetään kuitenkin NumPy-kirjaston array-tyyppiä, johon tutustutaan kierroksesta 4 lähtien.
Listat sanakirjojen sisällä
Sanakirjan arvot voivat olla vaikka listoja:
yhdisteet = {"C2H6": ["C", 2, "H", 6],
"NaCl": ["Na", 1, "Cl", 1]
# indeksi: 0 1 2 3
}
print(yhdisteet["C2H6"])
print("Yhdisteessa C2H6 on", yhdisteet["C2H6"][3], "vetyatomia")
tulostaa
['C', 2, 'H', 6]
Yhdisteessa C2H6 on 6 vetyatomia
Sisäkkäiset sanakirjat
Sanakirjoja voi laittaa sisäkkäin:
tietokanta = {
"C2H6": {"moolimassa": 30.07, "tiheys": 1.36},
"NaCl": {"moolimassa": 58.44, "tiheys": 2.16}
}
print("Etaanin tiheys on:", tietokanta["C2H6"]["tiheys"], "g/cm^3")
print("Ruokasuolan moolimassa on:", tietokanta["NaCl"]["moolimassa"], "g/mol")
tulostaa
Etaanin tiheys on: 1.36 g/cm^3
Ruokasuolan moolimassa on: 58.44 g/mol
Tehtävä 3.7.1
Merkkijonojen käsittely listoina
Merkkijonot ovat läheistä sukua listoille. Merkkijonon voi muuntaa suoraan listaksi:
merkkijono_listana = list('Sana')
print("Merkkijono listana:", merkkijono_listana)
tulostaa
Merkkijono listana: ['S', 'a', 'n', 'a']
Merkkijonon voi siis itsessään ajatella olevan "lista merkkejä". Näin ollen myös merkkijonoja voi indeksoida ja siivuttaa:
teksti = "Kemisti" # indeksi: 0123456 print(teksti[0]) print(teksti[0:4])
tulostaa
K
Kemi
Merkkijonosta voi etsiä toisen merkkijonon sijainnin str.index-funktiolla:
merkkijono = "Huomio!!?"
# indeksi: 012345678
print(merkkijono.index("!!"))
tulostaa
6
Merkkijonofunktiot str.split ja str.join
Funktio str.split pilkkoo merkkijonon listaksi. Esimerkiksi:
teksti = "Sc Ti V Cr Mn Co Fe Ni Cu Zn" alkuaineet = teksti.split() print(alkuaineet)
tulostaa
['Sc', 'Ti', 'V', 'Cr', 'Mn', 'Co', 'Fe', 'Ni', 'Cu', 'Zn']
Oletuksena merkkijonosta poimitaan välilyönnillä erotetut alkiot. Tätä voi muuttaa sep-parametrillä:
teksti = "4, 21, 53, 12, 7, 0" numerot = teksti.split(sep = ',') print(numerot)
tulostaa
['4', ' 21', ' 53', ' 12', ' 7', ' 0']
Funktion str.split käänteisoperaatio on str.join. Funktiolle annetaan parametrina lista ja se yhdistää listan alkiot merkkijonoksi:
alkuaineet = ['B', 'C', 'N', 'O', 'F', 'Ne'] teksti = " ".join(alkuaineet) print(teksti)
tulostaa
B C N O F Ne
Listan alkioiden väliin lisätään .join-funktiokutsua edeltävä merkkijono. Esimerkiksi:
alkuaineet = ['B', 'C', 'N', 'O', 'F', 'Ne'] teksti = ", ".join(alkuaineet) print(teksti)
tulostaa
B, C, N, O, F, Ne
Merkkijonon sisällön tutkiminen merkki kerrallaan for-silmukan avulla
Pythonin dokumentaatiossa listataan useita merkkijonojen käsittelyyn tarkoitettuja funktioita. Katsotaan, kuinka merkkijonon sisältöä voi tutkia merkki kerrallaan for-silmukan avulla.
Funktiolla str.isdigit voi etsiä numeroita:
# Käydään katuosoite läpi merkki kerrallaan ja poimitaan numerot
katuosoite = "Kemistintie 23"
numerot = ""
for merkki in katuosoite:
if merkki.isdigit():
numerot = numerot + merkki
print("Talon numero on", numerot)
tulostaa
Talon numero on 23
Funktiolla str.isalpha voi etsiä kirjaimia:
# Käydään postinumero läpi merkki kerrallaan ja poimitaan kirjaimet
postinumero = "02150 ESPOO"
kirjaimet = ""
for merkki in postinumero:
if merkki.isalpha():
kirjaimet = kirjaimet + merkki
print("Postitoimipaikka on", kirjaimet)
tulostaa
Postitoimipaikka on ESPOO
Funktioilla str.isupper ja str.islower voi tutkia, onko merkki iso vai pieni kirjain. str.isspace kertoo, onko merkki "whitespace", eli esimerkiksi välilyönti, tabulaattori tai rivinvaihto:
# Kerätään alkuainesymbolit listaan
teksti = "Sc Ti V Cr Mn Co Fe Ni Cu Zn "
alkuaineet = []
apujono = ""
# Käydään teksti läpi kirjain kerrallaan
for merkki in teksti:
# Alkuaineen symboli alkaa aina isolla kirjaimella
if merkki.isupper():
# Iso kirjain talteen
apujono = merkki
elif merkki.islower():
# Lisätään pieni kirjain ison alkukirjaimen perään
apujono = apujono + merkki
elif merkki.isspace():
# Välilyönti erottaa symbolit, eli apujono sisältää nyt alkuainesymbolin
# Symboli on joko (a) iso kirjain + pieni kirjain tai (b) vain iso kirjain
alkuaineet.append(apujono)
apujono = ""
print(alkuaineet)
tulostaa
['Sc', 'Ti', 'V', 'Cr', 'Mn', 'Co', 'Fe', 'Ni', 'Cu', 'Zn']
Tehtävä 3.8.1
Kierros 4
Neljännellä kierroksella otamme käyttöön numpy-kirjaston, joka sisältää luonnontieteissä ja tekniikassa erityisen hyödyllisen tietorakenteen, eli taulukon (array). Taulukoiden avulla voimme helposti ja tehokkaasti kuvata vektoreita, matriiseja ja mitä tahansa N-ulotteisia datajoukkoja. Tutustumme myös tietotyyppeihin, joilla on helppo käsitellä polynomeja.
Lisäksi otamme käyttöön matplotlib-kirjaston, jolla pystymme visualisoimaan ja analysoimaan dataa. Upeita kuvaajia luvassa!
Tehtävä 4.0.1.
NumPy-kirjasto
NumPy-kirjasto sisältää numeerisen laskennan kannalta keskeisiä työkaluja:
- ndarray (tai array) -tietorakenne eli taulukko. Taulukoilla voidaan kuvata esimerkiksi vektoreita, matriiseja ja mitä tahansa moniulotteisia datajoukkoja. Numpy-taulukot soveltuvat erittäin hyvin esimerkiksi mittausdatan käsittelyyn ja ne mahdollistavat numeerisen laskennan aivan eri tasolla kuin tavalliset listat.
- Lukuisia funktioita taulukoiden käsittelyyn:
- Matemaattiset perusfunktiot (sin, cos, exp)
- Lineaarialgebra (matriisit ja vektorit)
- Tilastolliset funktiot, polynomit, datan sovitus, jne.
- Numpy-taulukot ja niiden käsittelyyn liittyvät funktiot on toteutettu mahdollisimman tehokkaasti ja ne soveltuvat hyvinkin raskaaseen laskentaan
Jos haluat tehdä numeerista laskentaa Pythonilla, käytä NumPy-kirjastoa. NumPy + SciPy + Matplotlib –yhdistelmällä voi korvata monessa asiassa Matlabin.
Matplotlib-kirjastoa käytämme jo tällä kierroksella kuvaajien tekemiseen. SciPy:stä opimme lisää kurssin viimeisellä kierroksella.
Jos haluat oppia NumPystä enemmän kuin tämän kurssin puitteissa on mahdolista, suosittelen Nicolas P. Rougierin materiaaleja:
- From Python to NumPy-kirja: http://www.labri.fr/perso/nrougier/from-python-to-numpy/index.html
NumPy-taulukot (array)
NumPy-taulukoita ja muita NumPyn ominaisuuksia käytettäessä ohjelmaan pitää aina tuoda numpy-moduuuli import-käskyllä. Tällä kurssilla moduuli tuodaan aina seuraavalla käskyllä, jolloin NumPyn funktioita voi kutsua lyhennettä np käyttäen:
import numpy as np
Taulukoiden luominen ja alkioihin viittaaminen
Taulukoita (array) voi luoda suoraviivaisesti numpy.array-funktion avulla.
Yksiulotteiset taulukot (vektorit)
Luodaan yksiulotteinen neljan alkion taulukko (eli vektori)
vektori = np.array([10, 20, 30, 40]) # indeksi: 0 1 2 3
Taulukon ulottuvuus (engl. dimension) tarkoittaa, montako indeksiä tarvitaan yhden alkion osoittamiseen. Yksiulotteisen esimerkkivektorin tapauksessa tarvitsemme vain yhden indeksin, joka saa arvot 0-3.
Taulukon alkiohin viittaaminen toimii kuten listojen kanssa (muista, että ensimmainen indeksi on 0):
eka = vektori[0] # 10 toka = vektori[1] # 20 vika_1 = vektori[3] # 40 vika_2 = vektori[-1] # 40
Kaksiulotteiset taulukot (matriisit)
Luodaan kaksiulotteinen kahden rivin ja kolmen sarakkeen taulukko (eli matriisi):
matriisi = np.array([[10, 20, 30],
[40, 50, 60]])
Erona tavallisiin listoihin kaksiulotteisten NumPy-taulukkojen alkioihin voi viitata käytännöllisellä taulukko[rivi, sarake] -merkinnällä:
ekan_rivin_eka_sarake = M[0, 0] # 10 tokan_rivin_toka_sarake = M[1, 1] # 50 tokan_rivin_vika_sarake = M[1, -1] # 60
Myös tavallisista listoista tuttu merkintä taulukko[rivi][sarake] toimii, mutta se on kömpelömpi käyttää.
Kolmiulotteiset taulukot
Luodaan viimeisenä esimerkkinä kolmiulotteinen 2 x 2 x 3 taulukko:
T = np.array([[[1, 2, 3],
[4, 5, 6]],
[[10, 20, 30],
[40, 50, 60]
]])
alkio = T[1, 1, 0] # 40
Taulukon ulottuvuuksien tarkastelu (ndim, shape, len)
Minkä tahansa NumPy-taulukon ulottuvuuksien määrän voi selvittää ndim-funktiolla:
matriisi = np.array([[10, 20, 30],
[40, 50, 60]])
matriisin_ulottuvuus = np.ndim(matriisi) # palauttaa kokonaisluvun 2
shape-funktio palauttaa taulukon ulottuvuuksien dimensiot
# Käytetään yllä määriteltyä taulukkoa T T_dimensiot = np.shape(T) # palauttaa monikon (2, 2, 3)
Tuttu len-funktio palauttaa taulukon halutun ulottuvuuden pituuden:
# Käytetään yllä määriteltyjä taulukoita vektori ja T vektorin_pituus = len(vektori) # palauttaa kokonaisluvun 4 T_kolmas_ulottuvuus_pituus = len(T[0, 0]) # palauttaa kokonaisluvun 3
Taulukon suurimman tai pienimmän alkion indeksin etsiminen
NumPy-taulukon suurimman alkion indeksin voi etsiä argmax-funktiolla. Pienimmän alkion indeksi löytyy vastaavasti argmin-funktiolla. Jos tarvitset vain taulukon suurimman tai pienimmän arvon ilman indeksiä, käytä amax ja amin-funktioita:
luvut = np.array([3.1, 1.0, 0.4, 10.1])
print(f"Suurin luku: {np.amax(luvut):.1f}")
print(f"Suurimman luvun indeksi: {np.argmax(luvut):d}")
print(f"Pienin luku: {np.amin(luvut):.1f}")
print(f"Pienimmän luvun indeksi: {np.argmin(luvut):d}")
tulostaa
Suurin luku: 10.1
Suurimman luvun indeksi: 3
Pienin luku: 0.4
Pienimmän luvun indeksi: 2
Listojen muuntaminen taulukoiksi
Yllä käytetty numpy.array-funktio muuntaa tavallisen listan NumPy-taulukoksi. Seuraavassa esimerkissä vektori v1 luodaan kokonaislukujen listasta [1, 2, 3, 4, 5]:
v1 = np.array([1, 2, 3, 4, 5])
Saman muunnoksen voi tehdä myös olemassaoleville listoille (tai monikoille):
lista = [1.1, 2.2, 3.3, 4.4]
v2 = np.array(lista)
# nyt v2 on array([ 1.1, 2.2, 3.3, 4.4])
M1 = np.array([lista, lista])
# Nyt M1 on kaksiulotteinen taulukko
# array([[ 1.1, 2.2, 3.3, 4.4],
# [ 1.1, 2.2, 3.3, 4.4]])
Nollilla alustetun taulukon luominen
Joskus on tarpeellista luoda ensin tyhjä nollilla alustettu taulukko, johon voi sitten lisätä dataa myöhemmin. Nollilla alustetun taulukon voi luoda numpy.zeros-funktiolla:
vektori = np.zeros(8) # Kahdeksan alkiota pitkä vektori täynnä nollia matriisi = np.zeros((9, 9)) # 9x9 matriisi täynnä nollia. zeros-funktion parametri on tässä monikko (9, 9).
Moniulotteisen taulukon tapauksessa numpy.zeros-funktion parametrin shape tulee olla monikko tai lista.
Kokonaislukuja sisältävien taulukoiden luominen arange-funktiolla
Kokonaislukuja sisältäviä taulukoita voi luoda range-funktiota vastaavalla numpy.arange-funktiolla:
v3 = np.arange(1, 10) # np.arange(alku, loppu) # Nyt v3 on array([1, 2, 3, 4, 5, 6, 7, 8, 9]) # Huomaa, että viimenen alkio on loppu-1 (kuten range-funktiolla)
Myös muoto np.arange(alku, loppu, askel) on käytössä:
v4 = np.arange(2, 11, 2) # Nyt v4 on array([ 2, 4, 6, 8, 10])
Liukulukuja sisältävien taulukoiden luominen linspace-funktiolla
Liukulukuja sisältäviä taulukoita voi luoda numpy.linspace-funktiolla, jota kutsutaan numpy.linspace(start, stop, num). Parametri start on ensimmäinen luku, stop on viimeinen luku ja num on lukujen määrä välillä start..stop. Huomaa, etta oletuksena stop-luku tulee mukaan, toisin kuin arange-funktiossa!
v5 = np.linspace(0.1, 1, 10) # v5 on array([ 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ]) v6 = np.linspace(-0.2, 0.2, 6) # v6 on array([-0.2 , -0.12, -0.04, 0.04, 0.12, 0.2 ])
Tällä kurssilla linspace-funktio on isossa roolissa esimerkiksi kuvaajia piirrettäessä. arange-funktiota käytämme vain vähän.
linspace-funktiota voi käyttää myös kokonaislukujen kanssa, mutta tällöin pitää vain tiedostaa, että tuloksena syntyvän taulukon luvut ovat liukulukuja, eivät kokonaislukuja:
v7 = np.linspace(-5, 5, 11) # v7 on array([-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.])
Jos tarvitset tasavälisiä lukuja logaritmisella asteikolla, voit käyttää funktiota numpy.logspace.
Tehtävä 4.2.1
NumPy-taulukoiden siivuttaminen
Luodaan ensin uusi yksiulotteinen taulukko (vektori):
import numpy as np v = np.arange(100, 1100, 100) # v on array([ 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000]) # indeksi: 0 1 2 3 4 5 6 7 8 9
NumPy-taulukoiden siivuttaminen toimii samaan tapaan kuin listojen siivuttaminen. Merkinnässä [start:stop:askel], stop-alkio ei kuulu enää siivuun. askel-osuus ei ole pakollinen.
Siivutetaan yllä luotu vektori v:
siivu1 = v[0:4] # siivu1 on array([100, 200, 300, 400]) siivu2 = v[5:7] # siivu2 on array([600, 700]) siivu3 = v[0:7:2] # siivu3 on array([100, 300, 500, 700])
NumPy-tarjoaa myös erittain käytannöllisen : -indeksoinnin Matlabin tapaan. : -indeksi tarkoittaa kyseisen ulottuvuuden kaikkia indeksejä:
# Määritellään 3 x 4 matriisi M
M = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
# Matriisin M kaikkien rivien kolmas sarake
A = M[:, 2] # array([ 3, 7, 11])
# Matriisin M toisen rivin kaikki sarakkeet
B1 = M[1, :] # array([5, 6, 7, 8])
# Rivin siivuttamisen voi tehdä myös merkinnällä, jossa sarakkeet jätetään pois
B2 = M[1] # array([5, 6, 7, 8])
:-indeksointia voi käyttää myös näin:
# Poimitaan matriisin M kaikkien rivien joka toinen sarake A2 = M[:, 0::2]
jolloin taulukko A2 saa arvon:
array([[ 1, 3],
[ 5, 7],
[ 9, 11]])
Merkintä M[:, 0::2] tarkoittaa siis, että poimitaan
- kaikilta riveiltä (kaksoispiste ennen pilkkua)
- ensimmäisestä sarakkeesta lähtien (0)
- viimeiseen sarakkeeseen asti (stop-arvo puuttuu)
- kahden sarakkeen askelvälillä (2).
Tehtävä 4.3.1
Laskuoperaatiot NumPy-taulukoilla
Luodaan ensin uusi taulukko (yksiulotteinen vektori):
import numpy as np v1 = np.arange(100, 1001, 100) # v1 on array([ 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000])
NumPy-taulukoiden ja yksittäisten lukuarvojen laskuoperaatiot onnistuvat suoraviivaisesti. NumPy suorittaa laskuoperaation jokaiselle alkiolle:
v2 = v1 + 1 # array([ 101, 201, 301, 401, 501, 601, 701, 801, 901, 1001]) v3 = v1 * 2 # array([ 200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000]) v4 = v1 / 100 # array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.]) v42 = 100 / v1 # array([ 1., 0.5, 0.33333333, 0.25, 0.2, 0.16666667, 0.14285714, 0.125, 0.11111111, 0.1])
NumPy-taulukoita voi myos lisätä, kertoa ja jakaa keskenään. Operaatiot tehdaan alkioittain, joten taulukoiden tulee olla samankokoisia!
v5 = v2 + v2 # array([ 202, 402, 602, 802, 1002, 1202, 1402, 1602, 1802, 2002]) v6 = v4 * v4 # array([ 1., 4., 9., 16., 25., 36., 49., 64., 81., 100.]) v7 = v3 / v1 # array([ 2., 2., 2., 2., 2., 2., 2., 2., 2., 2.])
Seuraavassa esimerkissä matriisin M sarakkeiden määrä (4) täsmää vektorin a pituuden (4) kanssa. Jokainen rivivektori kerrotaan alkioittain vektorilla a:
M = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
a = np.array([1, 2, 3, 4])
tulo = M * a
# Ensimmäinen rivi on siis [1*1, 2*2, 3*3, 4*4]
# array([[ 1, 4, 9, 16],
# [ 5, 12, 21, 32],
# [ 9, 20, 33, 48]])
Huomaa, että esimerkin kertolasku M * a on aivan eri asia kuin oikea matriisitulo! Siitä lisää seuraavassa luvussa.
Laskutoimitukset ilman silmukoita
Tarkastellaan esimerkin avulla, kuinka NumPy-taulukoiden kanssa toimitaan listoihin verrattuna. Aiemmin olemme oppineet, kuinka kahdesta listasta lasketaan tuloksia kolmanteen:
massat = [2.2, 4.1, 5.6, 1.2, 6.7]
moolimassat = [18.015, 58.44, 74.55, 81.408, 144.645]
ainemaarat = []
for massa, moolimassa in zip(massat, moolimassat):
ainemaarat.append(massa / moolimassa)
NumPyllä for-silmukkaa ei tarvita:
import numpy as np massat = np.array([2.2, 4.1, 5.6, 1.2, 6.7]) moolimassat = np.array([18.015, 58.44, 74.55, 81.408, 144.645]) ainemaarat_np = massat / moolimassat
NumPy jakaa siis taulukon massat jokaisen alkion taulukon moolimassat vastaavalla alkiolla ja lopputulos on uusi taulukko ainemaarat.
Molemmissa tapauksissa lasketut ainemäärät ovat samat. Mutta Numpyn tapa on merkittävästi nopeampi, varsinkin kun kyseessä on vähänkin isompi datamäärä. NumPyn lähestymistapaa kutsutaan vektoroinniksi.
Laajempi esimerkki
Toteutetaan funktio ainemaara NumPy-taulukoiden avulla:
import numpy as np
def ainemaara(m, M):
# m, M: massa (g) ja moolimassa (g/mol)
# Kukin parametri voi olla joko NumPy-taulukko tai yksittäinen luku
# Oletetaan, että kaikki parametrit ovat kelvollisia lukuarvoja
# Paluuarvo: ainemäärä(t)
# Jos yksikin parametri on NumPy-taulukko, paluuarvo on NumPy-taulukko
return m / M
# Luodaan kolmen alkiota sisältävät taulukot massoista ja moolimassoista
massat = np.array([3.2, 0.5, 2.2])
moolimassat = np.array([58.44, 42.394, 120.921])
# NaCl LiCl RbCl
# Lasketaan ja tulostetaan ainemäärät. Funktio palauttaa taulukon.
n1 = ainemaara(massat, moolimassat)
print(n1)
# Funktio toimii myös yksittäisillä lukuarvoilla
# Tässä tapauksessa funktio palauttaa yksittäisen liukuluvun
n2 = ainemaara(3.2, 58.44)
print(n2)
# Funktio toimii myös jos toinen parametri on yksittäinen luku ja toinen taulukko
# Tässä tapauksessa funktio palauttaa taulukon
n3 = ainemaara(3.2, moolimassat)
print(n3)
tulostaa
[0.05475702 0.01179412 0.0181937 ]
0.05475701574264203
[0.05475702 0.07548238 0.02646356]
Tehtävä 4.4.1
NumPyn matemaattiset funktiot
Aloitetaan luomalla yksiulotteinen taulukko v:
import numpy as np v = np.arange(1, 11) # v on array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
Summaus ja tulo
NumPyn matemaattisille funktioille annetaan parametrina taulukko, jolloin funktio suorittaa halutun matemaattisen operaation kaikille taulukon alkioille.
Taulukoiden alkioiden summaus ja tulo onnistuu numpy.sum ja numpy.prod-funktioilla:
summa = np.sum(v) # Tulos on 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 tulo = np.prod(v) # Tulos on 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 = 3628800
Laskutoimituksia voi tehdä myös taulukosta leikatuille siivuille:
# Määritellään 3 x 4 matriisi M
M = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
ekan_rivin_summa = np.sum(M[0]) # 1 + 2 + 3 + 4 = 10
vikan_sarakkeen_summa = np.sum(M[:, -1]) # 4 + 8 + 12 = 24
Matemaattiset funktiot
Lista NumPyn matemaattisista funktioista: https://docs.scipy.org/doc/numpy/reference/routines.math.html
Esimerkkejä vektorille v:
log_kympit = np.log10(v) # array([ 0. , 0.30103 , 0.47712125, 0.60205999, 0.69897 , # 0.77815125, 0.84509804, 0.90308999, 0.95424251, 1. ]) asteet = np.linspace(0, 360, 9) # array([ 0., 45., 90., 135., 180., 225., 270., 315., 360.]) radiaanit = np.radians(asteet) sinit = np.sin(radiaanit)
Tilastolliset funktiot
Lista NumPyn tilastollisista funktioista: https://docs.scipy.org/doc/numpy/reference/routines.statistics.html
Esimerkkejä vektorille v:
keskiarvo = np.mean(v) # 5.5 suurin = np.amax(v) # 10 pienin = np.amin(v) # 1
Taulukoiden yhtäsuuruuden vertailu alkioittain
Kahden taulukon yhtäsuuruutta voi verrata numpy.allclose-funktiolla, joka vertaa taulukoita alkioittain:
T1 = np.linspace(1.0, 5.0, 5)
# array([ 1., 2., 3., 4., 5.])
T2 = np.linspace(1.00001, 5.0, 5)
# array([ 1.00001 , 2.0000075, 3.000005 , 4.0000025, 5. ])
if np.allclose(T1, T2, rtol = 0.01):
print("Samat")
# Taulukoiden T1 ja T2 alkiot ovat yhtäsuuret 1% tarkkuudella (rtol = 0.01), joten tulostuu "Samat"
Lineaarialgebra
Lista NumPyn lineaarialgebran funktioista: https://docs.scipy.org/doc/numpy/reference/routines.linalg.html
Matriisitulon voi laskea numpy.matmul-funktiolla
# Määritellään kaksi 2x2 neliömatriisia A ja B
A = np.array([[2, 1],
[1, 2]])
B = np.array([[2, 2],
[3, 3]])
# Matriisitulo C = AB
C = np.matmul(A, B)
# Nyt C on:
#array([[7, 7],
# [8, 8]])
# Muistathan, että vaihdantalaki ei päde matriisien kertolaskussa!
# Matriisitulo D = BA
D = np.matmul(B, A)
# Nyt D on:
# array([[6, 6],
# [9, 9]])
Eli np.matmul(A, B) != np.matmul(B, A).
Tehtävä 4.5.1
Tehtävä 4.5.2
Matplotlib-kirjasto
Matplotlib-kirjasto sisältää erittäin monipuoliset työkalut erilaisten kuvaajien tekemiseen. Tällä kurssilla tutustumme matplotlib.pyplot-moduuliin, joka mahdollistaa kuvaajien piirtämisen hieman Matlabin tapaan.
Kun teet Matplotlib-tehtäviä Spyderissä, kuvaajien pitäisi aueta siististi suoraan IPython-konsolin yllä olevalle Plots-välilehdelle. Asiasta kerrotaan lisää Spyderin käyttöohjeissa.
Jos ajat esimerkin
import numpy as np import matplotlib.pyplot as plt X = np.arange(1, 101) Y = np.sqrt(X) plt.plot(X, Y) plt.show()
konsoli tulostaa:
Figures now render in the Plots pane by default. To make them also appear inline in the Console, uncheck "Mute Inline Plotting" under the Plots pane options menu.
ja kun klikkaat Plots-välilehteä konsolin yläpuolelta, näet siellä kuvaajan:
Jos haluat, että matplotlib piirtää kuvaajat suoraan IPython-konsoliin, seuraa Spyderin antamia ohjeita.
Jos et käytä Spyderiä vaan jotain muuta kehitysympäristöä (esim. PyCharm tai VS Code), sinun pitää itse selvittää, miten Matplotlib-kuvaajat toimivat sen kanssa. Voi olla, että ne avautuvat omina ikkunoinaan.
Hyviä lisämateriaaleja
- Matplotlibin sivusto sisältää paljon esimerkkikoodeja ja -kuvaajia: https://matplotlib.org/stable/gallery/index.html
- Suosittelen myös Nicolas P. Rougierin oppimateriaaleja: https://github.com/rougier/matplotlib-tutorial
matplotlib.pyplot-moduuli
Matplotlib-kuvaajia piirrettäessä ohjelmaan pitää aina tuoda matplotlib.pyplot-moduuli import-käskyllä. Matplotlibiä käytettäessä tarvitaan useimmiten myös NumPy-moduuli. Tällä kurssilla nämä moduulit tuodaan aina seuraavilla käskyllä, jolloin voidaan käyttää lyhenteitä np ja plt:
import numpy as np import matplotlib.pyplot as plt
Yksinkertainen kuvaaja oletusasetuksilla
Aloitetaan piirtämällä yksinkertainen kuvaaja funktiolle f(x) = 2x oletusasetuksia käyttäen
import numpy as np import matplotlib.pyplot as plt # Luodaan datat funktiolle f(x) = 2x X = np.linspace(1, 100, 100) Y = X * 2 # Luodaan kuvaaja datoja X ja Y käyttäen plt.plot(X, Y) # Näytetään kuvaaja plt.show()
Lopputulos:
Kuvaajan oletusasetuksien muuttaminen
matplotlib.pyplot.plot-funktion parametrejä muokkaamalla voi vaikuttaa kuvaajan ulkonäköön. Lyhyt yhteenveto parametrien mahdollisista arvoista seuraavassa luvussa.
import numpy as np
import matplotlib.pyplot as plt
# Luodaan datat
X = np.linspace(1, 100, 10)
Y = X * 2
# Luodaan kuvaaja
# - Vaihdetaan tyyliksi pisteet ('o')
# - Vaihdetaan väri color-parametrilla punaiseksi
plt.plot(X, Y, 'o', color = 'red')
# Näytetään kuvaaja
plt.show()
Lopputulos:
Akseleiden muokkaaminen, selitteiden lisääminen ja kuvien tallentaminen
Muokataan esimerkkikuvaajaa edelleen
import numpy as np
import matplotlib.pyplot as plt
# Luodaan datat
X = np.linspace(1, 100, 100)
Y = X * 2
# Luodaan katkoviiva-kuvaaja (mukana väri ja teksti 'f(x) = 2x' selitettä varten)
plt.plot(X, Y, '--', color = 'red', label = 'f(x) = 2x')
# Nimetään akselit
plt.xlabel('x')
plt.ylabel('y')
# Asetetaan akselivali
plt.xlim(0, 100)
plt.ylim(0, 200)
# Asetetaan akselin numerot (ticks)
plt.xticks(np.arange(0, 101, 10))
plt.yticks(np.arange(0, 201, 20))
# Lisätään selite (legend). Se käyttää plot-funktion label-parametriä.
plt.legend(loc = 'upper left')
# Lisätään otsikko (title)
plt.title('Hieno kuvaaja')
# Tallennetaan kuvaaja myös png ja PDF-muodossa
plt.savefig("kuvaaja.png", dpi = 300)
plt.savefig("kuvaaja.pdf")
# Lopuksi piirretaan kuvaaja
plt.show()
Lopputulos:
Kuvaajan voi siis tallentaa tiedostoon plt.savefig-funktiolla. Kuvaajat tallentuvat samaan hakemistoon, missä ohjelma ajetaan (paitsi jos annat plt.savefig-funktiolle kokonaisen tiedostopolkun, esimerkiksi "C:\Users\pipetti\hienokuva.pdf").
Huom! plt.savefig-funktiota pitää kutsua ennen plt.show-funktiota. Matplotlib päättelee tiedoston tyypin sen päätteestä. Tyypillisiä vaihtoehtoja ovat pdf, eps ja png (png-kuvien tarkkuutta voi nostaa dpi-parametrilla).
Useampi kuvaaja samassa akselistossa
Matplotlibillä on helppo piirtää useita kuvaajia samaan akselistoon. Riittää, kun kutsuu plt.plot-funktiota useamman kerran:
import numpy as np import matplotlib.pyplot as plt # Luodaan kolmet XY-datat X1 = np.linspace(1, 100, 100) Y1 = X1 * 2 X2 = np.linspace(1, 100, 100) Y2 = X2 * 4 X3 = np.linspace(1, 100, 100) Y3 = X3 * 6 # Luodaan kolme kuvaajaa # Huomaa lyhennetty merkintä, jossa yhdistetty väri ja viivan tyyppi plt.plot(X1, Y1, 'b-', label = 'f(x) = 2x') plt.plot(X2, Y2, 'r--', label = 'f(x) = 4x') plt.plot(X3, Y3, 'g-.', label = 'f(x) = 6x') # Asetetaan akselien rajat ja luodaan selite plt.xlim(0, 100) plt.ylim(0, 600) plt.legend(loc = 'upper left') # Näytetään kuvaajat plt.show()
Lopputulos:

Muuntyyppiset kuvaajat
Matplotlib.pyplot-moduuli sisältää valtavasti erilaisia toiminnallisuuksia. Erityyppisiä kuvaajia on lukuisia. Hyödyllisiä kuvaajatyyppejä ovat varmasti esimerkiksi pyplot.scatter (XY-pistekuvaaja) ja pyplot.bar (pylväsdiagrammi).
Lisämateriaalia
- https://matplotlib.org/stable/gallery/index.html
- https://matplotlib.org/stable/api/pyplot_summary.html
- https://github.com/rougier/matplotlib-tutorial
Tehtävä 4.7.1
Tehtävä 4.7.2
Matplotlib-määritelmiä
Ajantasainen yhteenveto matplotlib.pyplot.plot-funktion parametreista löytyy osoitteesta: https://matplotlib.org/devdocs/api/_as_gen/matplotlib.pyplot.plot.html#matplotlib.pyplot.plot
Alla lyhyt yhteenveto.
Viivatyypit:
Värit (katso myös http://matplotlib.org/api/colors_api.html)
Selitteen (legend) sijainti (plt.legend-funktio)
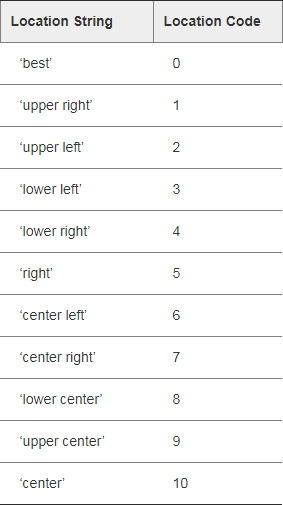
NumPy-polynomit
Kemian tekniikassa haluamme usein sovittaa polynomeja mittausdataan. Polynomien käsittelyssä voimme käyttää numpy.poly1d-toimintoa (varsinaisesti kyseessä on "luokka", joita käsitellään olio-ohjelmoinnin yhteydessä kurssin 6. kierroksella).
Polynomien luominen
import numpy as np
import matplotlib.pyplot as plt
# Luodaan polynomi x^2 + 4x + 3
# Kutsutaan poly1d:tä kertoimilla [1, 4, 3], eli 1*x^2 + 4*x^1 + 3*x^0
pol = np.poly1d([1, 4, 3])
print("Polynomi on (eksponentit ylärivillä):\n", pol)
tulostaa
Polynomi on (eksponentit ylärivillä): 2 1 x + 4 x + 3
Polynomien perusominaisuudet
# Polynomin arvon laskeminen yksittäisessä pisteessä
pol = np.poly1d([1, 4, 3])
print("Arvo pisteessa x = 5:", pol(5))
# Laskee siis 5^2 + 5*4 + 3 = 48
# Polynomin juuret (nollakohdat): pol.r
print("Juuret:", pol.r)
# Polynomin derivaatta: pol.deriv
# pol.deriv palauttaa uuden polynomin (poly1d-olion )
der = pol.deriv()
print("Derivaatta:", der)
print("Derivaatan arvo pisteessä x = 5:", der(5))
tulostaa
Arvo pisteessa x = 5: 48 Juuret: [-3. -1.] Derivaatta: 2 x + 4 Derivaatan arvo pisteessä x = 5: 14
Polynomeilla laskeminen ja kuvaajien piirtäminen
# Polynomilla voi tehdä laskutoimituksia pol = np.poly1d([1, 4, 3]) print(pol**2)
tulostaa (eksponentit ylärivillä)
4 3 2 1 x + 8 x + 22 x + 24 x + 9
# Polynomin arvon voi laskea myös useassa pisteessä X = np.arange(0, 11) # X on array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) Y = pol(X) # Y on array([ 3, 8, 15, 24, 35, 48, 63, 80, 99, 120, 143]) # Luodaan polynomin kuvaaja plt.plot(X, Y) plt.show()
Kuvaaja on:

Polynomisovitukset
Polynomisovituksia voi tehdä np.polyfit-funktiolla. Tarkastellaan esimerkkiä:
import numpy as np import matplotlib.pyplot as plt # Luodaan XY-datat X = np.array([-4.1, -3.4, -2.2, 1.1, 2.2, 3.3, 4.4, 5.5]) Y = np.array([20.91, 15.46, 8.94, 5.11, 8.94, 14.79, 23.46, 34.15]) # Luodaan raakadatan kuvaaja plt.plot(X, Y, 'o', label = 'raakadata') # Sovitusfunktio: np.polyfit(xdata, ydata, polynomin_aste) # Tehdään raakadatalle toisen asteen polynomisovitus: kertoimet = np.polyfit(X, Y, 2) # kertoimet on nyt NumPy-taulukko, joka sisältää sovitetun polynomin kertoimet [a, b, c]: # array([ 0.9996726 , -0.00626338, 4.00940658]) # a * x^2 b * x c * 1 # Tehdään kertoimista sovituspolynomi (np.poly1d) sovitus = np.poly1d(kertoimet) # sovitus on nyt poly1d-olio, jolla on sovitetun polynomin kertoimet: # poly1d([ 0.9996726 , -0.00626338, 4.00940658]) # HUOMAA, että merkintä sovitus[2] palauttaa 2. asteen termin kertoimen 0.9996726! # np.polyfit- funktion tapauksessa 2. asteen termi on kertoimet[0]! # Lasketaan sovituspolynomin y-arvot usealle x-arvolle pol_X = np.linspace(-5.0, 6.0, 50) pol_Y = sovitus(pol_X) # Luodaan sovituspolynomin kuvaaja # Kuvaaja lisätään plt.plot-funktiolla samaan kuvaan raakadatan kanssa plt.plot(pol_X, pol_Y, color = 'red', label = 'sovitus (2. aste)') plt.legend(loc = 'upper left', frameon = False) plt.show()
Lopputulos:

Korrelaatiokerroin
Suorien sovittamisen yhteydessä voi laskea X- ja Y-datojen välisen Pearsonin korrelaatiokertoimen np.corrcoef-funktiolla. Kahden muuttujan välinen korrelaatio kertoo mahdollisesta lineaarisesta riippuvuudesta. Jos korrelaatiokerroin on lähellä arvoa 1, voidaan toisen muuttujan arvo arvioida tietämällä vain toisen arvo. Mitä lähempänä korrelaatiokerroin on nollaa, sitä enemmän arvioituun arvoon liittyy epävarmuutta.
numpy.corrcoef -funktiolle annetaan X- ja Y-datapisteet, jolloin se palauttaa korrelaatiokertoimet 2×2 taulukkona [[xx, xy], [yx, yy]]. Useimmiten riittää, että poimimme taulukosta xy-korrelaation, eli indeksin [0, 1].
import numpy as np
import matplotlib.pyplot as plt
# Luodaan taulukot mittausarvoista
konsentraatiot = np.array([0.1, 0.2, 0.3, 0.4, 0.5])
absorbanssi = np.array([2.24, 4.02, 6.11, 8.27, 10.56])
# Luodaan kuvaaja raakadatoista
plt.plot(konsentraatiot, absorbanssi, 'o', label = 'raakadata')
# Sovitusfunktio: np.polyfit(xdata, ydata, polynomin_aste)
# Tehdään 1. asteen polynomisovitus XY-dataan:
kertoimet = np.polyfit(konsentraatiot, absorbanssi, 1)
# kertoimet on nyt NumPy-taulukko, joka sisältää sovitetun polynomin kertoimet
# Tehdään kertoimista polynomi np.poly1d
polynomi = np.poly1d(kertoimet)
# Lasketaan y:n arvot usealle x:n arvolle
pol_X = np.linspace(0.0, 0.6, 60)
pol_Y = polynomi(pol_X)
# Luodaan sovituspolynomin kuvaaja
# Kuvaaja lisätään plot-funktiolla samaan kuvaan raakadatan kanssa
plt.plot(pol_X, pol_Y, color = 'blue', label = 'sovitus (1. aste)')
# Kuvaajan asetukset
plt.xlabel('Konsentraatio (mol/l)')
plt.ylabel('Absorbanssi')
plt.xlim(0, 0.6)
plt.ylim(0, 12)
plt.legend(loc = 'upper left', frameon = False)
plt.show()
# Lasketaan Pearsonin korrelaatiokerroin ja sen neliö
R = np.corrcoef(konsentraatiot, absorbanssi)[0, 1]
R_toiseen = R**2
print(f"Sovituksen R^2 on: {R_toiseen:.3f}")
Lopputuloksena saadaan kuvaaja:
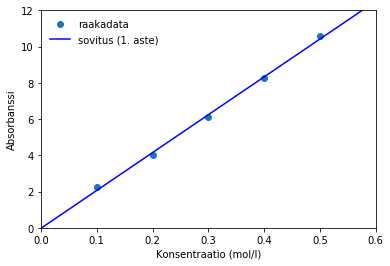
ja tulostus
Sovituksen R^2 on: 0.998
Eli tässä tapauksessa X- ja Y-arvojen välillä on erittäin vahva lineaarinen korrelaatio (absorbanssi on suoraan verrannollinen konsentraatioon).
Tehtävä 4.9.1
Kierros 5
Tiedostojen käsittely
Viidennellä kierroksella tutustumme tiedostojen käyttöön Pythonissa. Tietojen lukeminen tiedostosta ja kirjoittaminen tiedostoon on aivan keskeinen tehtävä ohjelmoinnissa.
Huomioitavaa tiedostojen hallinnasta
- 5. kierroksen tehtäviä tehdessäsi sinulla olisi hyvä olla jonkinlainen kokonaiskuva tiedostojen hallinnasta käyttämässäsi käyttöjärjestelmässä (Windows, MacOS tai Linux).
- Kun kirjoitat ohjelmakoodin, joka luo uuden tiedoston, ohjelmasi luo tiedoston oletuksena samaan hakemistoon, missä ohjelman .py-tiedosto sijaitsee.
- Luomme kurssilla pääasiassa tekstitiedostoja. Voit tarkastella luomasi tiedoston sisältöä yksinkertaisesti avaamalla tekstitiedoston mihin tahansa tekstieditoriin (onnistuu yleensä kaksoisklikkaamalla tiedostoa). Voit avata tiedoston myös Spyderiin.
- Kun tehtävässä pitää luoda tekstitiedosto, kannattaa aina tarkistaa luomasi tiedoston sisältö tekstieditorilla!
- Kun tehtävässä pitää lukea olemassaolevan tekstitiedoston sisältö, kannattaa aina ensin tarkastella tiedostoa tekstieditorissa, jotta hahmotat paremmin, mitä tiedoston lukeminen vaatii ohjelmakoodiltasi.
Virheenkäsittely
Kierroksen aiheisiin kuuluu myös virheenkäsittely. Ohjelmien suorituksessa tulee usein vastaan virhetilanteita, joista pitäisi selvitä kunnialla (käyttäjä antaa luvun sijasta merkkijonon, avattava datatiedosto onkin tyhjä, jne...). Opettelemme käyttämään try-except-finally -rakenteita virheenkäsittelyyn.
Tehtävä 5.0.1
Tiedostojen avaaminen ja käsittely
Tiedostojen avaaminen open-funktiolla
Tiedostot avataan Pythonissa open-funktiolla, jota kutsutaan näin:
tiedosto = open(tiedoston_nimi_merkkijonona, tila)
Esimerkiksi komento
datat = open("data.txt", "r")
avaa tiedoston data.txt lukemista varten (parametrin tila arvo on "r", eli read).
Toinen esimerkki, missä kysytään avattavan tiedoston nimi käyttäjältä:
nimi = input("Anna avattavan tiedoston nimi")
tiedosto = open(nimi, "r")
Oletuksena avattava tiedosto avataan samasta hakemistosta, missä ohjelmaa suoritetaan. Tyypillisesti tämä on sama hakemisto, missä ohjelman .py-tiedosto sijaitsee.
Voit antaa avattaessa myös kokonaisen tiedostopolun:
datat = open("Z:\datat\data.txt", "r")
Parametrin tila tyypillisimmät arvot ovat
- "r" eli read: avataan tiedosto lukemista varten:
- "w" eli write: avataan tiedosto kirjoittamista varten:
- Jos tiedostoa ei ole olemassa, open luo uuden tiedoston
- Jos tiedosto on jo olemassa, open luo uuden tyhjän tiedoston olemassaolevan tiedoston päälle
- "a" eli append: avataan tiedosto kirjoittamista varten:
- Jos tiedostoa ei ole olemassa, open luo uuden tiedoston
- Jos tiedosto on jo olemassa, tiedostoon kirjoitettavat tiedot lisätään sen loppuun (ei tyhjennä tiedostoa kuten "w")
Tiedostojen käsittely
open-funktio joka palauttaa ns. tiedosto-olion. jonka avulla tiedostoa voi käsitellä. Avataan tiedosto mittaukset.txt lukemista varten:
mittaukset = open("Z:\fyke\mittaukset.txt", "r")
Muuttuja mittaukset on nyt tiedosto-olio, jonka avulla tiedostoa käsitellään. Esimerkiksi ensimmäisen rivin lukeminen tiedostosta onnistuisi näin:
rivi = mittaukset.readline()
Tiedoston lukemisesta ja tiedostoon kirjoittamisesta kerrotaan lisää yksityiskohtia seuraavassa luvussa. Tällä kurssilla käsittelemme vain tekstitiedostoja ja tähän käytämme pääasiassa for-silmukkaa.
Tiedostojen sulkeminen close-funktiolla
Kun tiedoston käsittely lopetetaan se pitää sulkea close-funktiolla:
mittaukset = open("Z:\fyke\mittaukset.txt", "r")
rivi1 = mittaukset.readline()
print("Eka rivi:", rivi1)
mittaukset.close()
Tiedoston sulkeminen on erittäin tärkeää! Jos kirjoitat tiedostoon, mutta jätät tiedoston sulkematta, tiedot eivät välttämättä tallennu!
Tehtävä 5.1.1
Datan lukeminen ja kirjoittaminen
Luodaan tiedosto halogeenit.txt, joka sisältää halogeenien symbolit. Voimme kirjoittaa tiedostoon käyttämällä write()-funktiota:
halogeenit = ['F', 'Cl', 'Br', 'I']
# Avataan uusi tiedosto kirjoittamista varten
tiedosto = open("halogeenit.txt", "w")
# Käydään halogeenit-lista läpi for-silmukan avulla
for halogeeni in halogeenit:
# Kirjoitetaan jokainen listan alkio omalle rivilleen (\n on rivinvaihto)
# Kirjoittamiseen käytetään write()-funktiota
tiedosto.write(halogeeni + "\n")
# Lopuksi suljetaan tiedosto!
tiedosto.close()
Luetaan seuraavaksi juuri luomamme tiedoston sisältö rivi kerrallaan. Hyödynnetään for-silmukkaa:
halogeenit1 = []
halogeenit2 = []
tiedosto = open("halogeenit.txt", "r")
# Seuraava for-silmukka lukee tiedostosta rivin kerrallaan.
# Silmukkamuuttuja "rivi" päivittyy jokaisella silmukan kierroksella kunnes
# kaikki tiedoston rivit on luettu
for rivi in tiedosto:
halogeenit1.append(rivi)
# str.rstrip()-funktio poistaa rivinvaihdon rivin lopusta
halogeenit2.append(rivi.rstrip())
# Suljetaan tiedosto!
tiedosto.close()
print(halogeenit1)
print(halogeenit2)
Koodi tulostaa:
['F\n', 'Cl\n', 'Br\n', 'I\n'] ['F', 'Cl', 'Br', 'I']
Eli str.rstrip-funktiolla päästin eroon tiedostossa olleista rivinvaihtomerkistä, jotka Python sisällyttää lukemiinsa riveihin.
str.split-funktion ja f-merkkijonojen hyödyntäminen
Luodaan tiedosto neliot.txt, joka sisältää numerot 1-100 ja niiden neliöt välilyönnillä erotettuna. Tiedoston rakenne on siis (kolme ensimmäistä riviä):
1 1
2 4
3 9
Huomaa, miten f-merkkijonoja voidaan hyödyntää myös tiedostoon kirjoitettaessa:
tiedosto = open("neliot.txt", "w")
for i in range(1, 101):
tiedosto.write(f"{i:d} {(i * i):d}\n")
tiedosto.close()
Avataan luotu tiedosto lukemista varten ja hyödynnetään aiemmin kierroksella 3 mainittua str.split-funktiota:
tiedosto = open("neliot.txt", "r")
for rivi in tiedosto:
# rivi on siis merkkijono, esim. "3 9\n". Funktio str.split() palauttaa
# listan, johon merkkijonon sanat on pilkottu alkioiksi.
# Jos siis rivi on "3 9\n", rivi.split() palauttaa listan ["3", "9"]
# str.split-funktio siivoaa myös rivinvaihdot (\n) pois
# Funktion palauttamat arvot voi lukea suoraan muuttujiin:
luku, nelio = rivi.split()
# Toinen vaihtoehto olisi lukea arvot listaan ja poimia ne sieltä:
# datat = rivi.split()
# luku = datat[0]
# nelio = datat[1]
# Luvut ovat nyt edelleen merkkijonoina. Ne voisi muuntaa
# kokonaisluvuiksi int()-funktiolla, mutta nyt riittää tulostus
print("Luvun", luku, "nelio on", nelio)
tiedosto.close()
Koodi tulostaa alla olevat rivit (vain kolme ensimmäistä ja kolme viimeistä riviä näkyvissä):
Luvun 1 neliö on 1
Luvun 2 neliö on 4
Luvun 3 neliö on 9
...
Luvun 98 neliö on 9604
Luvun 99 neliö on 9801
Luvun 100 neliö on 10000
Numeroarvojen lukeminen tiedostosta
Meillä on käytössämme datatiedosto moolimassat.txt, joka sisältää kullakin rivillä yhdisteen nimen, moolimassan (g/mol) ja massan (g) välilyönneillä
erotettuna. Tiedoston kaksi ensimmäistä riviä näyttävät tältä:
H2O 18.015 2.3 NaCl 58.44 4.5
Luetaan nyt tiedoston sisältö niin, että voimme hyödyntää lukuarvoja laskennassa
tiedosto = open("moolimassat.txt", "r")
for rivi in tiedosto:
datat = rivi.split()
# datat on nyt kolmen merkkijonon lista, esim.: ["H2O", "18.015", "2.3"]
nimi = datat[0]
moolimassa = float(datat[1])
massa = float(datat[2])
ainemaara = massa / moolimassa
print(f"Yhdisteen {nimi} ainemaara on {ainemaara:4.3f} mol")
# Lopuksi suljetaan tiedosto
tiedosto.close()
Koodi alla olevat rivit (vain kolme ensimmäistä riviä näkyvissä):
Yhdisteen H2O ainemaara on 0.128 mol Yhdisteen NaCl ainemaara on 0.077 mol Yhdisteen KF ainemaara on 0.114 mol ...
Toinen esimerkki numeroarvojen lukemisesta
Meillä on käytössämme datatiedosto temps.txt, joka sisältää kullakin rivillä alkuaineen symbolin, nimen, sulamispisteen (°C) ja kiehumispisteen (°C). Tiedoston kaksi ensimmäistä riviä näyttävät tältä:
Sc, skandium , 1541.0 ,2830 Ti , titaani , 1668.0,3287
Huomaa, että tiedot ovat nyt pilkulla eroteltuna ja sisältävät ylimääräisiä välilyöntejä. Luetaan nyt tiedoston sisältö hyödyntämällä str.split-funktion sep-parametriä, jolla voi määrätä datapisteiden välisen erottimen. Lisäksi tarvitsemme str.strip-funktiota ylimääräisten välilyöntien poistamiseen.
metallit = []
tiedosto = open("temps.txt", "r")
for rivi in tiedosto:
datat = rivi.split(sep = ',')
# datat on nyt neljän merkkijonon lista, esim.: ["Sc", " skandium ", "1541.0 ", "2830"]
# Käytetään lisäksi str.strip()-funktiota, joka karsii tyhjät merkit
# (välilyönnit, rivinvaihdot) merkkijonon vasemmalta ja oikealta puolelta.
# Esimerkiksi " testi \n".strip() palauttaa "testi"
symboli = datat[0].strip()
nimi = datat[1].strip()
# sulamispiste ja kiehumispiste liukulukuina. str.strip()-funktiota ei tarvita,
# float osaa jättää ylimääräiset välilyönnit huomioimatta
sulamispiste = float(datat[2])
kiehumispiste = float(datat[3])
print(f"Alkuaineen {symboli:2s} sulamispiste on {sulamispiste:4.0f} C ja kiehumispiste {kiehumispiste:4.0f} C")
# Lopuksi suljetaan tiedosto!
tiedosto.close()
Koodi tulostaa (vain kolme ensimmäistä riviä näkyvissä):
Alkuaineen Sc sulamispiste on 1541 C ja kiehumispiste 2830 C Alkuaineen Ti sulamispiste on 1668 C ja kiehumispiste 3287 C Alkuaineen V sulamispiste on 1910 C ja kiehumispiste 3407 C ...
Tehtävä 5.2.1
Tiedostojen helppo käsittely NumPy:llä
NumPy-kirjasto sisältää käteviä funktioita tiedostojen käsittelyyn. Nämä ovat hyödyllisiä etenkin numeerista dataa luettaessa. Tekstitiedostoja voi lukea ja kirjoittaa numpy.loadtxt- ja numpy.savetxt-funktioilla. Tarkastellaan esimerkkiä, jossa meillä on tilavuus- ja painedataa tiedostossa painedata.txt seuraavassa muodossa (kommenttirivi ja kolme ensimmäistä datariviä näkyvissä):
# V (dm^3) p (Pa) 0.21 1856455 0.31 1176944 0.41 838490
Esimerkki, kuinka tiedoston voi lukea numpy.loadtxt-funktiolla ja tulokset voi kirjoittaa tiedostoon numpy.savetxt-funktiolla:
import numpy as np
Vp_data = np.loadtxt("painedata.txt")
# Vp_data on nyt NumPy-taulukko, jossa on kaksi saraketta: V ja p
R = 8.314462618 # J K^-1 mol ^-1
n = 0.05 # mol
V = Vp_data[:, 0] / 1000 # 1. sarake (V, dm^3). Muunnetaan dm^3 -> m^3
p = Vp_data[:, 1] # 2. sarake (p, Pa)
T = V * p / (n * R) # K
np.savetxt("T.txt", T, fmt="%.3f", header = "T (K)")
loadtxt osaa automaattisesti jättää tiedoston alussa olevan, #-merkillä alkavan kommenttirivin lukematta. Tiedostoja ei tarvitse avata ja sulkea, koska loadtxt ja savetxt tekevät sen puolestasi.
Tulostiedoston T.txt neljä ensimmäistä riviä näyttävät tältä:
# T (K) 937.777 877.634 826.947
savetxt-funktion header-parametrin arvo tulee siis tiedoston alkuun kommenttiriviksi. fmt-parametrin rakenne on periaatteessa sama kuin str.format-funktiolla, mutta kaarisulut korvautuvat %-merkillä, eikä :-merkkiä käytetä. Lisätietoja numpy.savetxt-funktion ohjeesta.
Huom! Jos tarkastelet savetxt-tiedoston luomaa tiedostoa Windowsissa, rivinvaihdot eivät välttämättä näy oikein. Tämä johtuu siitä, etteivät monet Windows-ohjelmat ymmärrä \n-rivinvaihtoa oikealla tavalla. Tiedosto näkyy oikein esim. Spyderissä.
numpy.column_stack
Kun sinulla on useita yksiulotteisia taulukoita, jotka haluat tallentaa sarakkeina tiedostoon, numpy.column_stack on hyvin hyödyllinen funktio. Laajennetaan yllä olevaa esimerkkiä niin, että tallennamme tulostiedostoon myös alkuperäiset tilavuus- ja painedatat.
import numpy as np
Vp_data = np.loadtxt("painedata.txt")
R = 8.314462618 # J K^-1 mol ^-1
n = 0.05 # mol
V = Vp_data[:, 0] / 1000 # 1. sarake (V, dm^3). Muunnetaan dm^3 -> m^3
p = Vp_data[:, 1] # 2. sarake (p, Pa)
T = V * p / (n * R) # K
# Käytetään np.column_stack -funktiota, jolla yksiulotteiset
# NumPy-taulukot voi liittää yhteen kaksiulotteisen taulukon sarakkeiksi
VpT_data = np.column_stack([V * 1000, p, T]) # Tilavuudet m^3 -> dm^3
np.savetxt("VpT.txt", VpT_data, fmt="%10.3f %10.0f %10.1f",
header = "V (dm^3) p (Pa) T (K)")
Huomaa, miten fmt-parametrille annetaan oma muotoiluparametri jokaiselle sarakkeelle. Tiedoston VpT.txt neljä ensimmäistä riviä näyttävät tältä:
# V (dm^3) p (Pa) T (K)
0.210 1856455 937.8
0.310 1176944 877.6
0.410 838490 826.9
Tehtävä 5.4.1
rivi.strip()
Virhetilanteiden käsittely (try-except-finally)
Poikkeukset
Hyvässä ohjelmakoodissa varaudutaan aina erilaisiin virhetilanteisiin, kuten
- Käyttäjän antama virheellinen syöte
- Tiedoston avaaminen epäonnistuu
Pythonissa virhetilanteet hoidetaan poikkeusten (engl. exception) avulla.
Oletkin varmasti jo kohdannut lukuisia poikkeuksia kurssin aikana. Esimerkiksi jos olet yrittänyt muuntaa vääränlaista merkkijonoa lukuarvoksi komennolla
luku = int("kolme")
Python on ilmoittanut ValueError-poikkeuksesta:
ValueError: invalid literal for int() with base 10: 'kolme'
Poikkeusten "nappaaminen" ohjelmakoodissa
Virhetilanteessa Python "nostaa" (engl. raise) poikkeuksen. Poikkeuksen voi "napata" (engl. catch) ja käsitellä, jolloin se ei johda ohjelman suorituksen keskeytymiseen.
Poikkeusten nappaamiseen ja käsittelemiseen käytetään try-except -rakennetta. Napataan virheellisestä lukuarvosta johtuva ValueError-poikkeus:
while True:
try:
luku = float(input("Anna liukuluku:\n"))
# Jos suoritus jatkui tänne, käyttäjä antoi kelvollisen liukuluvun
break
except ValueError:
# Napataan ValueError-poikkeus (virheellinen lukuarvo)
print("Virheellinen lukuarvo!")
# Virhe on nyt käsitelty ja ohjelman suoritus palaa while-silmukan alkuun
print("Annoit luvun", luku)
Esimerkkisuoritus:
Anna liukuluku: > kolme piste kaksi Virheellinen lukuarvo! Anna liukuluku: > 3.2 Annoit luvun 3.2
Poikkeus tiedostoa avattaessa (OSError)
Tiedostoja käsitellessä voi tulla vastaan virhetilanteita (esimerkiksi yritetään avata tiedostoa, jota ei ole olemassa). Tällöin pitää napata virhe OSError:
# Luetaan rivit tiedostosta
try:
tiedosto = open("rivit.txt", "r")
for rivi in tiedosto:
print(rivi)
except OSError:
print("Virhe avattaessa tiedostoa rivit.txt")
Sisäkkäiset try-lausekkeet
Monesti tarvitaan sisäkkäisiä try-lausekkeita, joilla hoidetaan erityyppiset virheet. Hyvä nyrkkisääntö on, että try-avainsana tulisi olla mahdollisimman lähellä riviä, jossa odotat virheen tapahtuvan. Esimerkki:
nimi = "luku.txt"
try:
# Yritetään avata tiedosto, tämä voi johtaa virheeseen
tiedosto = open(nimi, "r")
# Tiedosto aukesi onnistuneesti, luetaan siitä
for rivi in tiedosto:
try:
# Yritetään muuntaa teksti liukuluvuksi
luku = float(rivi)
# Onnistui, tulostetaan luku
print("Tiedosto sisälsi luvun", luku)
except ValueError:
# float()-funktio aiheutti ValueError-virheen
print(f"Virheellinen lukuarvo {rivi.strip():s} tiedostossa {nimi:s}")
# Suljetaan lopuksi tiedosto
tiedosto.close()
except OSError:
# Tänne päädytään, jos open-funktio epäonnistui
print("Virhe avattaessa tiedostoa", nimi)
Jos kaikki menee hyvin, ohjelma tulostaa:
Tiedosto sisälsi luvun 1.0
Jos tiedostoa ei ole olemassa, ohjelma tulostaa:
Virhe luettaessa tiedostoa luku.txt
Jos tiedostossa on virheellisiä lukuja, ohjelma tulostaa esimerkiksi
Virheellinen lukuarvo 1.0a tiedostossa luku.txt
Tiedosto sisälsi luvun 2.0
try-except-finally
try-except-finally-rakenteella voidaan varmistaa, että jokin asia tehdään varmasti, vaikka virheitä syntyisi. Luetaan tekstiä tiedostosta ja napataan poikkeukset (tässä tapauksessa tiedosto sisältää ainoastaan tekstin "keukeu"):
nimi = "teksti.txt"
try:
# Yritetään avata tiedosto, tämä voi johtaa virheeseen
tiedosto = open(nimi, "r")
try:
# Tiedosto aukesi onnistuneesti, yritetään lukea tiedoston sisältö read()-funktiolla
teksti = tiedosto.read()
# Onnistui, tulostetaan sisältö
print("Tiedosto sisälsi tekstin", teksti)
except OSError:
# read()-funktio aiheutti OSError-virheen, tiedostoa ei voi lukea
print(f"Tiedostoa {nimi:s} ei voitu lukea")
finally:
# Suljetaan tiedosto riippumatta siitä, oliko virheitä vai ei
print("Suljetaan tiedosto")
tiedosto.close()
except OSError:
# Tänne päädytään, jos open-funktio epäonnistui.
print("Virhe avattaessa tiedostoa", nimi)
# Tiedostoa ei avattu, joten sitä ei tarvitse myöskään sulkea
Jos kaikki menee hyvin, ohjelma tulostaa:
Tiedosto sisälsi tekstin keukeu Suljetaan tiedosto
Jos tiedostoa ei ole olemassa, ohjelma tulostaa:
Virhe avattaessa tiedostoa teksti.txt
Jos tiedostossa on virheellisiä lukuja, ohjelma tulostaa
Tiedostoa teksti.txt ei voitu lukea Suljetaan tiedosto
Ohjelma siis sulkee viimeisenä tekonaan tiedoston. Tämä on tärkeää ja tiedostojen kanssa tuleekin aina käyttää try-finally -rakennetta. Helpoiten tämän vaatimuksen voi kuitata käyttämällä with-lausetta (ks. seuraava luku).
try-except-else(-finally)
try-except-rakenteeseen voi yhdistää myös else-osan, joka suoritetaan siinä tapauksessa, että try-osio ei aiheuttanut poikkeuksia:
try:
luku = float(input("Anna luku:\n"))
except ValueError:
print("Virheellinen luku")
else:
print("Annoit luvun", luku)
try-except-else-rakenteeseen voi yhdistää vielä finally-osan, jossa esimerkiksi suljetaan avatut tiedostot.
Lista Pythonin poikkeuksista
Mistä tietää, mikä poikkeus pitäisi napata? Tässä on listä Pythonin sisäänrakennetuista poikkeuksista. Tällä kurssilla tärkeimmät poikkeukset ovat OSError (virhe avattaessa tai käsitellessä tiedostoa) ja ValueError (virhe muunnettaessa tekstiä lukuarvoksi).
Monimutkaisemmissa ohjelmissa pitää ottaa huomioon myös erilaisten kirjastojen poikkeustilanteet. Oikeassa ohjelmistossa, jonka tehtävä on esimerkiksi valvoa kriittistä tuotantoprosessia, voikin olla enemmän virheenkäsittelykoodia kuin varsinaista toiminnallista koodia!
Tehtävä 5.5.1
Tiedostojen avaaminen with-lausekkeella
Pythonissa on kätevä with-lauseke, joka kutsuu automaattisesti close-funktiota kun tiedoston käyttö lopetetaan. Luetaan tiedosto moolimassat.txt käyttäen with-lauseketta:
with open("moolimassat.txt", "r") as mmtiedosto:
# Ylläoleva rivi avaa tiedoston "moolimassat.txt", jonka jälkeen
# se on käytettävissä "mmtiedosto"-nimisenä tiedosto-oliona
# sisennetyn rakenteen sisällä
rivi1 = mmtiedosto.readline()
# Tässä kohti ohjelma poistuu with-lausekkeesta (huomaa sisennyksen muutos)
# with-lauseke sulkee automaattisesti tiedosto-olion "mmtiedosto"
print(rivi1)
with-lauseke ja virheenkäsittely
Virheenkäsittelyn näkökulmasta with-lauseke korvaa siis seuraavan try-finally -rakenteen:
mmtiedosto = open("moolimassat.txt", "r")
try:
rivi1 = mmtiedosto.readline()
print(rivi1)
finally:
# Tämä osio suoritetaan aina
mmtiedosto.close()
Koska myös open-funktion mahdolliset virheet on tärkeää käsitellä, with-lausekkeesta on parasta käyttää seuraavaa muotoa:
try:
with open("moolimassat.txt", "r") as mmtiedosto:
rivi1 = mmtiedosto.readline()
print(rivi1)
except OSError:
print("Tiedoston moolimassat.txt avaaminen epaonnistui!")
Tämä viimeinen esimerkki on minimivaatimus virheenkäsittelylle tiedostoja avattaessa!
Tehtävä 5.6.1
Kierros 6
Kuudes ja viimeinen kierros sisältää uutena asiana Scipy-kirjaston, jossa on valtava määrä työkaluja tieteellistä laskentaa varten.
Kierroksen oppimateriaalissa käsitellään myös olio-ohjelmointia, jota harjoitellaan B-tehtävissä. Olio-ohjelmointi on hyvin tärkeä lähestymistapa modernissa ohjelmistotuotannossa, mutta lyhyellä peruskurssilla ehdimme tutustua siihen vain kevyesti.
Tehtävä 6.0.1
SciPy
SciPy on Pythonilla luotu tieteellisen laskennan infrastruktuuri, joka on vapaasti kaikken Python-ohjelmoijien käytettävissä. SciPy on laaja kokonaisuus ja olemmekin jo käyttäneet osia siitä:
- NumPy-kirjasto on osa SciPyä ja SciPyn eri toiminnot hyödyntävät hyvin paljon NumPy-taulukoita
- Matplotlib-kirjasto on osa SciPyä
- Jopa Spyderin interaktiivinen IPython-konsoli on osa Scipyä
SciPyn dokumentaatio löytyy osoitteesta https://docs.scipy.org/doc/scipy/reference/ ja samasta paikasta löytyy myös tutoriaali SciPyn erilaisista alamoduuleista. Alamoduuleja on toistakymmentä ja tällä kurssilla tutustumme niistä vain neljään:
- scipy.constants: Luonnonvakiot. Sanakirjan scipy.constants.physical_constants tietolähde on CODATA-tietokanta, jota tälläkin kurssilla olemme hyödyntäneet. Helppo tapa ottaa luonnonvakioiden tarkimmat tunnetut arvot käyttöön!
- scipy.stats: Tilastolliset työkalut, esimerkiksi lineaarinen regressio (scipy.stats.linregress)
- scipy.linalg: Lineaarialgebra, esimerkiksi matriisien käsittely ja yhtälönryhmän ratkaiseminen (scipy.linalg.solve)
- scipy.integrate: Integrointi, erityisesti differentiaaliyhtälöiden numeerinen integrointi (scipy.integrate.solve_ivp)
Oppimateriaalin seuraavissa kappaleissa annetaan käytännön esimerkkejä näiden alamoduulien hyödyntämisestä.
scipy.constants
Moduuli scipy.constants sisältää luonnonvakioita, joista yleisimmät voi ottaa käyttöön suoraan tuomalla pelkän scipy.constants-moduulin ohjelmaan:
import scipy.constants
print(f"Kaasuvakion R arvo on {scipy.constants.R:.7f} J K^-1 mol^-1")
tulostaa
Kaasuvakion R arvo on 8.3144626 J K^-1 mol^-1
physical_constants-sanakirja
scipy.constants sisältää myös sanakirjan scipy.constants.physical_constants, jonka muoto on:
physical_constants[name] = (arvo_liukulukuna, yksikkö_merkkijonona, epävarmuus_liukulukuna)
Sanakirjan avain on siis luonnonvakio ja arvo on kolmen alkion monikko (voit ajatella sitä listana). Sanakirja sisältää laajan valikoiman luonnonvakioita, joiden arvot tulevat CODATA-tietokannasta. Esimerkki sanakirjan käytöstä:
from scipy.constants import physical_constants as pc
m_e = pc["electron mass"][0]
m_e_yksikko = pc["electron mass"][1]
m_e_epavarmuus = pc["electron mass"][2]
print(f"Elektronin massa m_e on {m_e:.10e} {m_e_yksikko:s}")
print(f"Arvon epävarmuus on {m_e_epavarmuus:.2e} {m_e_yksikko:s}")
tulostaa
Elektronin massa m_e on 9.1093837015e-31 kg Arvon epävarmuus on 2.80e-40 kg
Yksikkömuunnokset
Moduuli sisältää myös arvoja yksikkömuunnoksia varten:
import scipy.constants
kcal_mol = float(input("Anna energia yksikoissä kcal/mol:\n"))
kJ_mol = kcal_mol * scipy.constants.calorie
print(f"Antamasi energia on SI-yksiköissä {kJ_mol:.3f} kJ/mol")
Tulostaa
Anna energia yksikoissä kcal/mol:
> 2.5
Antamasi energia on SI-yksiköissä 10.460 kJ/mol
Tehtävä 6.2.1
scipy.stats
scipy.stats-moduuli sisältää valtavan määrän erilaisia tilastollisia funktioita ja jakaumafunktioita. Tämän kurssin puitteissa tutustumme vain scipy.stats.linregress-funktioon, jolla voi tehdä lineaarisen regressioanalyysin esimerkiksi mittausdatoille. Käytännössähän kyse on samasta suoran yhtälön sovituksesta, mitä olemme jo tehneet numpy.polyfit-funktion avulla 1. asteen polynomeille. linregress-funktio on kuitenkin suunniteltu juuri lineaariseen regressioon ja se myös palauttaa enemmän tietoja sovituksesta. Funktio palauttaa esimerkiksi korrelaatiokertoimen ja keskivirheen. Lisäksi linregress on laskennallisesti tehokkaampi hyvin suurille datajoukoille.
Tutustutaan linregress-funktioon esimerkin avulla. Meillä on käytössämme tiedosto T_p_data.txt, jossa on esitetty paine lämpötilan funktiona kaasumaiselle yhdisteelle (n = 0.65 mol). Mittausolosuhteet ovat sellaiset, että voimme odottaa ideaalikaasulain olevan voimassa.Tehtävänä on ratkaista astian tilavuus V.
- pV = nRT, joten p = nRT / V
- Kun paine esitetään lämpötilan funktiona ja mittausdatat sovitetaan suoran yhtälöön, sovitussuoran kulmakerroin on nR/V. Eli V = nR / kulmakerroin.
- Luetaan siis datat tiedostosta, tehdään niille lineaarinen regressio linregress-funktiolla ja ratkaistaan tilavuus V.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import linregress
from scipy.constants import R
n = 0.65 # mol
try:
# Luetaan datat tiedostosta
T_p_datat = np.loadtxt("T_p_data.txt")
except OSError:
print("Tiedoston T_p_data.txt avaaminen epaonnistui")
else:
# Lukeminen onnistui, luodaan kaksi yksiulotteista taulukkoa
T = T_p_datat[:, 0]
p = T_p_datat[:, 1]
# Lineaarinen regressio. T == x, p == y
slope, intercept, r_value, p_value, std_err = linregress(T, p)
# Sovitussuoran yhtälö: y = slope * x + intercept
# Lasketaan sovitussuoran arvot mitatuille x-arvoille (taulukko T)
p_sovitetut = slope * T + intercept
# Piirretään mittausdatat ja sovitussuora
plt.plot(T, p, '.', color = 'red', label = 'Mittaukset (T, p)')
# r_value on korrelaatiokerroin
teksti = "Sovitus (R$^2$ = {:.3f})".format(r_value**2)
plt.plot(T, p_sovitetut, '-', color = 'black', label = teksti)
# Kuvaajan akselit ja muut asetukset.
plt.xlim(300, 400)
plt.ylim(100000, 150000)
plt.xticks(np.arange(300, 401, 20))
plt.yticks(np.arange(100000, 150001, 10000))
plt.xlabel('T (K)')
plt.ylabel('p (Pa)')
plt.legend(loc = 'upper left')
# Ratkaistaan V == n * R / slope
# Tulostetaan V ja kulmakertoimen keskivirhe std_err
print("V: {:.3f} m^3".format(n * R / slope))
print("Kulmakertoimen keskivirhe: {:.1f}".format(std_err))
Koodi tulostaa
V: 0.015 m^3 Kulmakertoimen keskivirhe: 6.9
ja piirtää allaolevan kuvaajan
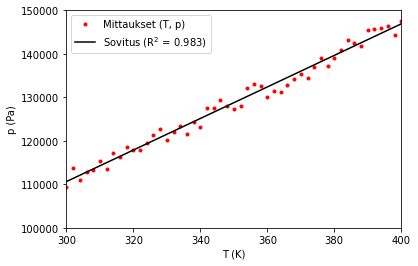
Tehtävä 6.3.1
scipy.linalg (Lineaarialgebra)
Moduuli scipy.linalg sisältää suuren määrän lineaarialgebraan liittyviä työkaluja (esim. matriisioperaatiot, ominaisarvo-ongelmien ratkaiseminen). Kappaleessa NumPyn matemaattiset funktiot mainittiin aiemmin moduuli numpy.linalg, joka sisältää samoja työkaluja. SciPyn lineaarialgebramoduuli on huomattavasti NumPy-moduulia laajempi.
Tämän kurssin puitteissa tutustumme vain funktioon scipy.linalg.solve, jolla voi ratkaista lineaarisia yhtälöryhmiä.
Hieman teoriaa
Tutustutaan yhtälöryhmien ratkaisemiseen Wikipedian sisältämän esimerkin avulla.
Määritellään lineaarinen kolmen yhtälön yhtälöryhmä:
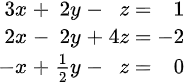
Yhtälöryhmässä on siis kolme (tuntematonta) muuttujaa x, y ja z. Ratkaistaan muuttujien arvot muuntamalla yhtälöryhmä matriisiyhtälöksi ja soveltamalla scipy.linalg.solve-funktiota.
Yhtälöryhmä, jossa on m kappaletta yhtälöitä ja n kappaletta muuttujia voidaan kirjoittaa yleisessä muodossa
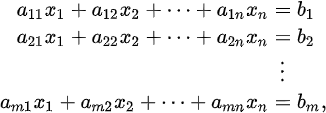
missä x1, x2, ..., xn ovat yhtälöryhmän tuntemattomat muuttujat,
a11, a12, ..., amn ovat yhtälöryhmän kertoimet ja
b1, b2, ..., bm ovat yhtälöryhmän vakiotermit.
Yhtälöryhmän ylläoleva yleinen muoto voidaan kirjoittaa myös vektorimuodossa
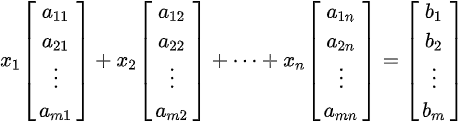
missä kertoimia ja vakiotermejä kuvataan sarakevektoreilla. Tämä vektorimuoto taas voidaan kirjoittaa matriisiyhtälönä
![]()
missä
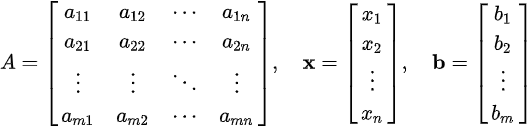
A on siis neliömatriisi, x ja b vektoreita. Nyt kun yhtälöryhmä on saatu matriisimuotoon, sen ratkaisemisessa voidaan hyödyntää lineaarialgebraa. Emme käsittele teoriaa tämän enempää vaan toteamme vain, että kun meillä on yhtälöryhmä matriisimuodossa Ax = b, voimme ratkaista sen scipy.linalg.solve-funktiolla näin helposti:
x = scipy.linalg.solve(A, b)
Esimerkki
Käytetään esimerkissä yllä esiteltyä yhtälöryhmää
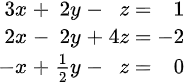
Nyt siis muuttujat x, y ja z vastaavat yhtälöryhmän yleisen muodon muuttujia x1, x2 ja x3. Ratkaistaan tuntemattomat:
import numpy as np
from scipy.linalg import solve
# A on 3x3 neliömatriisi
A = np.array([[ 3, 2, -1],
[ 2, -2, 4],
[-1, 1/2, -1]])
# b on kolmen alkion vektori
b = np.array([1, -2, 0])
# Ratkaistaan tuntemattomat muuttujat
x = solve(A, b)
print(x)
Koodi tulostaa
[ 1. -2. -2.]
Eli
x1 = x = 1,
x2 = y = -2 ja
x3 = z = -2
Ratkaisu on täsmälleen sama kuin Wikipediassa:
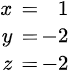
scipy.integrate.solve_ivp
Kemian tekniikassa haluamme usein ratkaista (integroida) differentiaaliyhtälöitä numeerisesti. SciPyn integrate-alamoduuli sisältää useita funktioita tätä varten. Tällä kurssilla tutustutaan scipy.integrate.solve_ivp-funktioon. Funktion solve_ivp käyttötarkoitus on: "Solve an initial value problem for a system of ordinary differential equations", eli kysessä on alkuarvotehtävän numeerinen ratkaisumenetelmä. Aiemmin alkuarvotehtävien ratkaisemiseen oli käytettävissä scipy.integrate.odeint-funktio, mutta nykyisin Scipyn kehittäjät suosittelevat hyödyntämään solve_ivp-funktiota.
Käydään läpi klassinen esimerkki, eli bakteeripopulaation eksponentiaalinen kasvu. Esimerkkisysteemimme osalta tiedetään, että bakteeripopulaation kasvunopeus dy/dt on suoraan verrannollinen populaation kokoon y ajan hetkellä t:
dy/dt = k * y
Tässä tapauksessa differentiaaliyhtälö on itse asiassa hyvin helppo ratkaista analyyttisesti suoralla integroinnilla (ks. Wikipedia-sivu). Mutta havainnollistetaan tämän suoraviivaisen esimerkin avulla, kuinka differentiaaliyhtälön numeerinen integrointi onnistuu SciPyllä.
Aja alla oleva esimerkki Spyderissä.
- Huomaa, miten dy/dt on määritelty funktiona f_dy_dt ja miten tämä funktio annetaan solve_ivp-funktion parametriksi.
- Lisäksi solve_ivp saa parametrina muuttujan y (bakteeripopulaatio) alkuarvon y_0 ja tutkittavat ajanhetket taulukossa t_eval.
- Käytännössä siis solve_ivp siis kutsuu funktiota f_dy_dt eri ajan hetkillä t, jolloin bakteeripopulaation koko on y.
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate
k = 0.92 # kasvunopeus
y_0 = np.array([500]) # bakteeripopulaatio alussa
def f_dy_dt(t, y):
# Differentiaaliyhtälön määritelmä eksponentiaaliselle kasvulle
# Parametri y on populaatio ajan hetkellä t
# Huomaa, että aikaparametria t ei tarvita tässä tapauksessa, mutta
# funktion määritelmän täytyy sisältää se
dy_dt = k * y
return dy_dt
# Simuloidaan ajanhetket t = [0, 4] h
max_t = 4 # tuntia
t = np.linspace(0, max_t, max_t * 4 + 1) # pisteet 0.25 h välein
# Differentiaaliyhtälön numeerinen integrointi
# fun -> Differentiaaliyhtälön dy/dt = f(t, y) oikea puoli.
# t_span -> Differentiaaliyhtälön numeerisen integroinnin alku- ja loppupiste.
# y0 -> Alkuarvot, eli bakteeripopulaatio alussa. Yksiulotteinen NumPy-taulukko.
# t_eval -> Ajanhetket, joissa bakteeripopulaatio lasketaan funktion f_dy_dt avulla. Yksiulotteinen NumPy-taulukko.
# Paluuarvo on ns. olio, joka sijoitetaan muuttujaan "tulos" (olioista kerrotaan lisää luvussa 7).
# Nyt meille riittää tieto, että voimme hyödyntää paluuarvoa seuraavalla tavalla:
# tulos.t -> ajanhetket, yksiulotteinen NumPy-taulukko
# tulos.y[0] -> Bakteeripopulaation määrä kullakin ajanhetkellä, yksiulotteinen NumPy-taulukko
tulos = scipy.integrate.solve_ivp(fun = f_dy_dt,
t_span = (t[0], t[-1]),
y0 = y_0,
t_eval = t)
# Piirretään kuvaaja
teksti = f"Bakteeripopulaatio (k = {k:.2f}, y_0 = {y_0[0]:d})"
plt.plot(tulos.t, tulos.y[0], color = 'red', label = teksti)
plt.xlim(0, max_t)
plt.ylim(0.0, 20000)
plt.xticks(np.linspace(0.0, 4.0, num = 9))
plt.yticks(np.arange(0, 20001, 2000))
plt.xlabel('t (h)')
plt.ylabel('Bakteeripopulaatio')
plt.legend(loc = 'upper left', frameon = False)
plt.show()
Lopputuloksena on seuraavan näköinen kuvaaja:
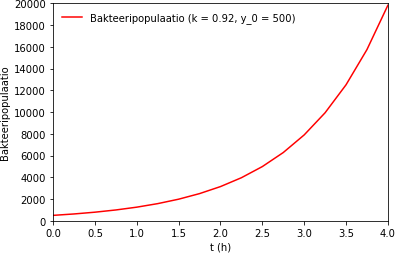
Huomaa, että solve_ivp-funktion parametri y0 voi olla myös vektori. Tällöin myös derivaatat laskeva funktio saa parametrikseen vektorin y ja solve_ivp palauttaa taulukon tulos.y, jossa on yhtä monta riviä kuin vektorissa y0 on alkioita.
Tehtävä 6.5.1
Olio-ohjelmointi
Aiemmin tällä kurssilla olemme tutustuneet erilaisiin tietorakenteisiin kuten listat, sanakirjat ja NumPy-taulukot. Olemme myös tutustuneet funktioihin, joilla näitä tietorakenteita voi käsitellä. Esimerkkinä vaikkapa max(lista), joka palauttaa listan suurimman alkion.
Tutustutaan nyt lyhyesti olioihin (engl. object). Voimme ajatella olioita tietorakenteina, jotka sisältävät myös tietojen käsittelyyn tarkoitettuja funktioita.
Luokan määritteleminen ja olioiden luominen
Jotta voimme luoda uuden olion, meidän pitää ensin määritellä luokka (engl. class) joka kuvaa olion ominaisuudet. Määritellään luokka Molekyyli (luokkien nimet kirjoitetaan isolla alkukirjaimella):
class Molekyyli:
def __init__(self, kaava, moolimassa):
self.kaava = kaava
self.moolimassa = moolimassa
def laske_ainemaara(self, massa):
return massa / self.moolimassa
Molekyyli-luokka sisältää kaksi funktiomäärittelyä. Näitä luokan sisältämiä funktioita kutsutaan metodeiksi (engl. method) erotuksena tavallisista funktioista, jotka eivät kuulu mihinkään luokkaan.
Molekyyli-luokka sisältää käynnistysmetodin __init__ ja metodin laske_ainemaara. Huomaa, että molempien metodien ensimmäinen parametri on self. Tämä parametri viittaa aina olioon itseensä. Python hoitaa self-parametrin automaattisesti, eli sitä ei anneta, kun metodia kutsutaan.
Käynnistysmetodissa __init__ luodaan oliolle kaksi kenttää: kaava ja moolimassa. Kenttiin pitää viitata metodin self-parametrin avulla.
Katsotaan, mitä määrittelemällämme luokalla voidaan nyt tehdä. Luodaan Molekyyli-luokkaan pohjautuvat oliot metaani ja etaani:
metaani = Molekyyli("CH4", 16.04)
etaani = Molekyyli("C2H6", 30.07)
Käsky Molekyyli("CH4", 16.04) tarkoittaa, että Molekyyli-luokan __init__-metodia kutsutaan parametreilla "CH4" ja 16.04 (self-parametria ei anneta, vaan Python antaa sen __init__-käynnistysmetodille automaattisesti). Käsky palauttaa uuden olion, jonka kentät kaava ja moolimassa on täytetty arvoilla "CH4" ja 16.04. Tämä olio sijoitetaan muuttujaan metaani.
Kokonainen olioesimerkki
Luokkamäärittelyn pohjalta voi luoda mielivaltaisen määrän uusia olioita. Katsotaan kokonaisen esimerkin avulla, miten olioiden kenttiä voi lukea ja miten niiden metodeja käytetään:
class Molekyyli:
def __init__(self, kaava, moolimassa):
self.kaava = kaava
self.moolimassa = moolimassa
def laske_ainemaara(self, massa):
return massa / self.moolimassa
metaani = Molekyyli("CH4", 16.04)
etaani = Molekyyli("C2H6", 30.07)
# Käytetään olioiden kenttiä
print(f"Metaanin molekyylikaava on {metaani.kaava}")
print(f"Etaanin molekyylikaava on {etaani.kaava}")
print(f"Metaanin moolimassa on {metaani.moolimassa} g/mol")
print(f"Etaanin moolimassa on {etaani.moolimassa} g/mol")
# Käytetään laske_ainemaara-metodia.
# Huomaa, että self-parametria ei anneta
n_metaani = metaani.laske_ainemaara(5.0) # 5 g metaania
n_etaani = etaani.laske_ainemaara(7.0) # 7 g etaania
print(f"5 g metaania on {n_metaani:.3f} mol")
print(f"7 g etaania on {n_etaani:.3f} mol")
tulostaa
Metaanin molekyylikaava on CH4 Etaanin molekyylikaava on C2H6 Metaanin moolimassa on 16.04 g/mol Etaanin moolimassa on 30.07 g/mol 5 g metaania on 0.312 mol 7 g etaania on 0.233 mol
Huomaa, miten laske_ainemaara-metodissa self.moolimassa viittaa kunkin olion omaan moolimassa-kenttään. Sillä on siis eri arvo metaanille ja etaanille. Näin ainemäärä lasketaan oikein kullekin oliolle. Parametri massa taas määritetään aina metodia laske_ainemaara kutsuttaessa.
Kannattaa tutustua esimerkkiin huolella. Esimerkki on yksinkertainen, mutta sen tarkoituksena on havainnollistaa, miten olioiden avulla voidaan yhdistää tietorakenteet ja funktiot samaan pakettiin. self-parametrin käyttö on yksi olio-ohjelmoinnin avainkäsitteistä.
Yllättävä käänne
Olemme itse asiassa käyttäneet olioita aivan koko kurssin ajan! Pythonissa oikeastaan kaikki asiat ovat olioita. Esimerkiksi int ja float -tyyppiset muuttujat tai list ja dict -tietorakenteet ovat kaikki olioita, jotka sisältävät myös metodeja kyseisten olioiden käsittelemiseksi:
# float-olio sisältää esimerkiksi is_integer()-metodin liukuluku = 3.14 print(liukuluku.is_integer()) liukuluku_int = 3.0 print(liukuluku_int.is_integer())
tulostaa
False
True
list-tietorakenne sisältää useita metodeja, joita olemmekin jo käyttäneet
lista = [1, 2, 3] # Tulostetaan ykkösten määrä listassa print(lista.count(1)) # Lisätään yksi ykkönen listaan lista.append(1) # Tulostetaan ykkösten määrä listassa print(lista.count(1))
tulostaa
1
2
Tehtävä 6.6.1
Kenttien luominen käynnistysmetodissa
Luokat voivat sisältää myös kenttiä, joita ei anneta käynnistysmetodin parametrina. On kuitenkin hyvä ohjelmointitapa alustaa myös nämä kentät käynnistysmetodissa. Tarkastellaan luokkaa Laboratorio, jossa kaksi kenttää annetaan käynnistysmetodin parametreina ja yksi kenttä alustetaan käynnistysmetodissa:
class Laboratorio:
def __init__(self, nimi, kapasiteetti):
# nimi: laboratorion nimi merkkijonona
# kapasiteetti: laboratorioon mahtuva opiskelijamäärä (kokonaisluku)
self.nimi = nimi
self.kapasiteetti = kapasiteetti
# Luodaan myös kenttä "opiskelijoita" (kokonaisluku), jonka arvo on alussa 0
self.opiskelijoita = 0
def lisaa_opiskelija(self):
# Mahtuuko labraan vielä?
if self.opiskelijoita < self.kapasiteetti:
# Kasvatetaan"opiskelijoita"-kenttää yhdellä
self.opiskelijoita += 1
print(f"Opiskelijoita nyt: {self.opiskelijoita}")
else:
print("Labra on täynnä!")
Kun luokan toteutusta testataan näin:
labra1 = Laboratorio("SEM", 3)
for i in range(4):
labra1.lisaa_opiskelija()
saadaan tulokseksi
Opiskelijoita nyt: 1 Opiskelijoita nyt: 2 Opiskelijoita nyt: 3 Labra on täynnä!
Jos haluat päästää opiskelijat pois labrasta, voit lisätä luokan toteutukseen metodin vapauta_opiskelija, joka vähentää labrasta yhden opiskelijan.
Olioiden säilöminen tietorakenteisiin
Oliot ovat jo itsessään kätevä tapa tietojen säilömiseksi. Olioita voi edelleen säilöä myös muihin tietorakenteisiin kuten listoihin tai sanakirjoihin.
Oliot listoissa
Tarkastellaan Molekyyli-luokkaan perustuvaa esimerkkiä:
class Molekyyli:
maara = 0
def __init__(self, kaava, moolimassa):
Molekyyli.maara += 1
self.kaava = kaava
self.moolimassa = moolimassa
def laske_ainemaara(self, massa):
return massa / self.moolimassa
metaani = Molekyyli("CH4", 16.04)
etaani = Molekyyli("C2H6", 30.07)
propaani = Molekyyli("C3H8", 44.10)
butaani = Molekyyli("C4H10", 58.12)
lista_olioista = [metaani, etaani, propaani, butaani]
print(f"Olet luonut {Molekyyli.maara} molekyyliä:")
for hiilivety in lista_olioista:
print(hiilivety.kaava)
Esimerkki tulostaa:
Olet luonut 4 molekyyliä: CH4 C2H6 C3H8 C4H10
Olioista koostuva lista on erittäin kätevä tapa korvata aiemmin kurssilla käytetyt rakenteet, joissa listojen sisään on säilötty toisia listoja:
lista_listoista = [["CH4", 16.04],
["C2H6", 30.07],
["C3H8", 44.10],
["C4H10", 58.12],
]
print(f"Listassa on {len(lista_listoista)} molekyyliä:")
for hiilivety in lista_listoista:
print(hiilivety[0])
Olioita sisältävät listat ovat joustava tietorakenne, koska luokkaan on helppo lisätä uusia kenttiä, eikä se vaikuta mitenkään listan määrittelyyn tai indeksointiin. Olioiden sisältämiin tietoihin on helppo viitata, koska olion kentillä on selkeä nimi. Sen sijaan listojen tapauksessa pitää aina muistaa, mikä indeksi vastasi mitäkin tietoa.
Oliot sanakirjoissa
Luodaan sanakirja, jonka avaimena on hiilivedyn nimi ja arvona Molekyyli-luokan olio:
class Molekyyli:
maara = 0
def __init__(self, kaava, moolimassa):
Molekyyli.maara += 1
self.kaava = kaava
self.moolimassa = moolimassa
def laske_ainemaara(self, massa):
return massa / self.moolimassa
sanakirja_olioista = {}
sanakirja_olioista["metaani"] = Molekyyli("CH4", 16.04)
sanakirja_olioista["etaani"] = Molekyyli("C2H6", 30.07)
sanakirja_olioista["propaani"] = Molekyyli("C3H8", 44.10)
sanakirja_olioista["butaani"] = Molekyyli("C4H10", 58.12)
print(f"Olet luonut {Molekyyli.maara} molekyyliä:")
for avain, hiilivety in sanakirja_olioista.items():
print(f"{avain} eli {hiilivety.kaava}")
Esimerkki tulostaa:
Olet luonut 4 molekyyliä: metaani eli CH4 etaani eli C2H6 propaani eli C3H8 butaani eli C4H10
Luokkamuuttujat
Edellisen luvun esimerkissä Molekyyli-luokalla oli kaksi kenttää, kaava ja moolimassa. Jokaisella Molekyyli-luokan pohjalta luodulla oliolla on omat arvonsa näissä kentissä. Joskus voi olla kuitenkin tarpeen säilyttää tietoa,
joka on kaikille luokan olioille yhteistä. Silloin voidaan hyödyntää luokkamuuttujia.
Lisätään Molekyyli-luokkaan luokkamuuttuja maara (määrä), jolla pidetään kirjaa Molekyyli-luokkaan perustuvien olioiden määrästä:
class Molekyyli:
maara = 0
def __init__(self, kaava, moolimassa):
# Kasvatetaan luokkamuuttujan maara arvoa
# Luokkamuuttujaan on viitattava luokan nimen avulla
Molekyyli.maara += 1
self.kaava = kaava
self.moolimassa = moolimassa
def laske_ainemaara(self, massa):
return massa / self.moolimassa
metaani = Molekyyli("CH4", 16.04)
etaani = Molekyyli("C2H6", 30.07)
propaani = Molekyyli("C3H8", 44.10)
print(f"Olet luonut {Molekyyli.maara} molekyyliä")
tulostaa
Olet luonut 3 molekyyliä
Luokkamuuttuja maara määritellään siis luokan metodien ulkopuolella. Se saa arvon 0, kun ohjelma käynnistyy (rivi "maara = 0" luokan määrittelyn alussa). Kun luokan pohjalta luodaan uusi olio, käynnistysmetodi kasvattaa luokkamuuttujan arvoa yhdellä (Molekyyli.maara += 1). Huomaa, että luokkamuuttujaan on viitattava luokan nimen avulla (Molekyyli.maara) sekä luokan metodien sisällä että luokkamäärittelyn ulkopuolella.
Tehtävä 6.7.1
Merkkijonometodi __str__
Viimeisenä olioesimerkkinä on luokka Alkuaine. Luokalla on käynnistysmetodin lisäksi kolme metodia on_kiintea, on_neste ja on_kaasu, joilla voi helposti tarkastella alkuaineen olomuotoa tietyssä lämpötilassa. Lisäksi luokalla on merkkijonometodi __str__, jonka tarkoitus on palauttaa luokan oliota kuvaava merkkijono. Tämä merkkijono tulostuu esimerkiksi jos print-funktiolle annetaan parametriksi luokan olio.
class Alkuaine:
def __init__(self, Z, symboli, nimi, atomipaino,
sulamispiste, kiehumispiste):
self.Z = Z
self.symboli = symboli
self.nimi = nimi
self.atomipaino = atomipaino
self.sulamispiste = sulamispiste # K
self.kiehumispiste = kiehumispiste # K
def __str__(self):
return(f"{self.symboli:s} ({self.nimi:s}): atomipaino = {self.atomipaino:.2f}")
def on_kiintea(self, T):
# Palauttaa True, jos alkuaine on kiinteä lampotilassa T (K)
return T < self.sulamispiste
def on_neste(self, T):
# Palauttaa True, jos alkuaine on neste lampotilassa T (K)
return T > self.sulamispiste and T < self.kiehumispiste
def on_kaasu(self, T):
# Palauttaa True, jos alkuaine on kaasu lampotilassa T (K)
return T > self.kiehumispiste
sinkki = Alkuaine(30, 'Zn', 'sinkki', 65.38, 693, 1180)
kadmium = Alkuaine(48, 'Cd', 'kadmium', 112.411, 594, 1040)
elohopea = Alkuaine(80, 'Hg', 'elohopea', 200.59, 234, 630)
T = 600 # K
for metalli in [sinkki, kadmium, elohopea]:
if metalli.on_neste(T):
print(f"{metalli.symboli} on neste lampotilassa {T} K")
else:
print(f"{metalli.symboli} ei ole neste lampotilassa {T} K")
# Käytetään __str__ -metodia kutsumalla print-funktiota
print("----------------------------------")
print(sinkki)
tulostaa
Zn ei ole neste lämpotilassa 600 K
Cd on neste lämpotilassa 600 K
Hg on neste lämpotilassa 600 K
----------------------------------
Zn (sinkki): atomipaino = 65.38
Tehtävä 6.8.1
Lisämateriaalia
Tämä kappale sisältää yleistä lisämateriaalia Python-ohjelmointiin liittyvistä aiheista.
Anacondan asennusohje
Tämä ei päde syksyn 2022 kurssilla (ks. alla): Aloita menemällä sivulle https://www.anaconda.com/products/distribution#Downloads
Valitse käyttöjärjestelmä, jota käytät ja lataa Python 3.9 tai uudempi.
HUOM! Tärkeä poikkeus syksyn 2022 kurssin osalta! Anacondan uusimpaan versioon Anaconda3-2022.05 sisältyy valitettavasti rikkinäinen versio Spyder-editorista (ohjelmat, joissa luetaan käyttäjän syötteitä input-funktiolla, eivät toimi). Ratkaisu on asentaa toiseksi uusin versio Anaconda3-2021.11. Suorat linkit näihin versioihin:
Windows: https://repo.anaconda.com/archive/Anaconda3-2021.11-Windows-x86_64.exe
MacOS: https://repo.anaconda.com/archive/Anaconda3-2021.11-MacOSX-x86_64.pkg
(nuo linkit on siis poimittu Anacondan virallisesta tiedostoarkistosta: https://repo.anaconda.com/archive/).
Jos olet jo asentanut Anacondan uusimman version Anaconda3-2022.05 ja Spyder antaa sinulle 1. kierroksen tehtävissä virheilmoituksen "got an unexpected keyword argument 'separator'", ratkaisu on poistaa Anacondan asennus ja asentaa toiseksi uusin versio.
Kun asennustiedosto (esim. Anaconda3-2020.02-Windows-x86_64.exe) on latautunut, käynnistä se ja seuraa asennusohjetta.
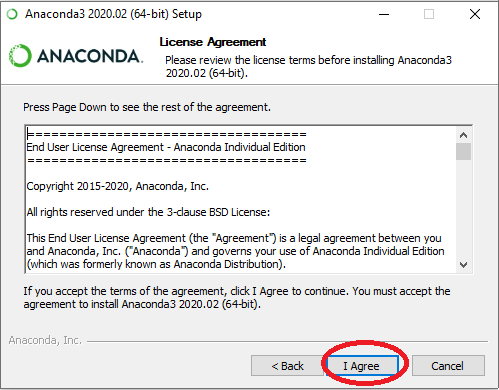
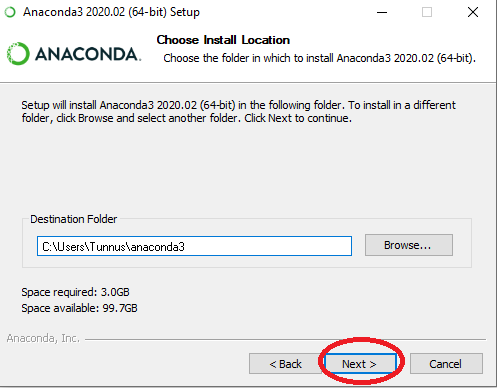

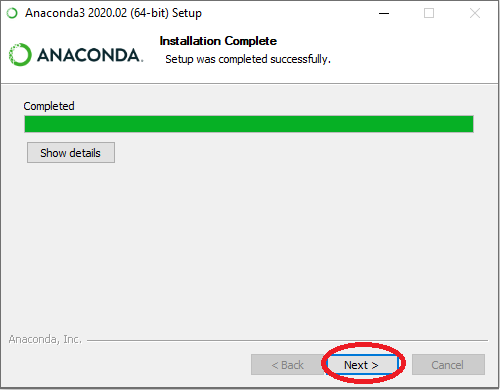

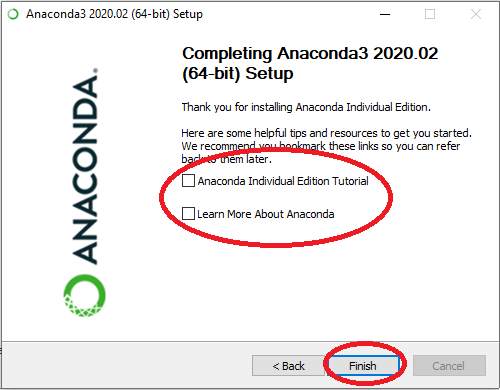
Spyder-kehitysympäristön saat avattua esimerkiksi kirjoittamalla spyder Windowsin aloitusvalikkoon ja avaamalla sovelluksen. Oppimateriaalin seuraavalla sivulla on Spyderin käyttöohjeita.
Spyder-käyttöohjeita
Spyder-kehitysympäristölle on olemassa useita käyttöoppaita sekä teksti- että videomuodossa. Tällä sivulla annetaan minimaaliset käyttöohjeet, joilla kurssilla pääsee liikkeelle. Spyderin käyttöön voi syventyä enemmän esimerkiksi seuraavien ohjemateriaalien avulla:
- Spyderin Help-valikko -> Interactive tours -> Introduction
- Spyderin Help-valikko -> Spyder tutorial
- Videomateriaalien ystäville YouTube on tutoriaaleja pullollaan (hakusanoina Spyder IDE)
Spyderin käynnistys
Jos käytät Windowsia, avaa Windowsin ohjelmistovalikko ja kirjoita spyder, jolloin Windowsin pitäisi tarjota sinulle ohjelmaa Spyder (Anaconda3). Valitse se.
Spyderin käynnistyminen voi kestää jopa minuutin. Ensimmäisellä käynnistyskerralla Spyder saattaa kysyä, haluatko asentaa Kite-lisäosan, jonka pitäisi helpottaa koodin kirjoittamista. En suosittele, koska en ole varma esimerkiksi kyseisen lisäosan tietoturvallisuudesta. Valitse siis Dismiss.
Spyderin toiminnot
Spyder ja sen keskeisimmät komennot on esitetty alla olevassa kuvassa:
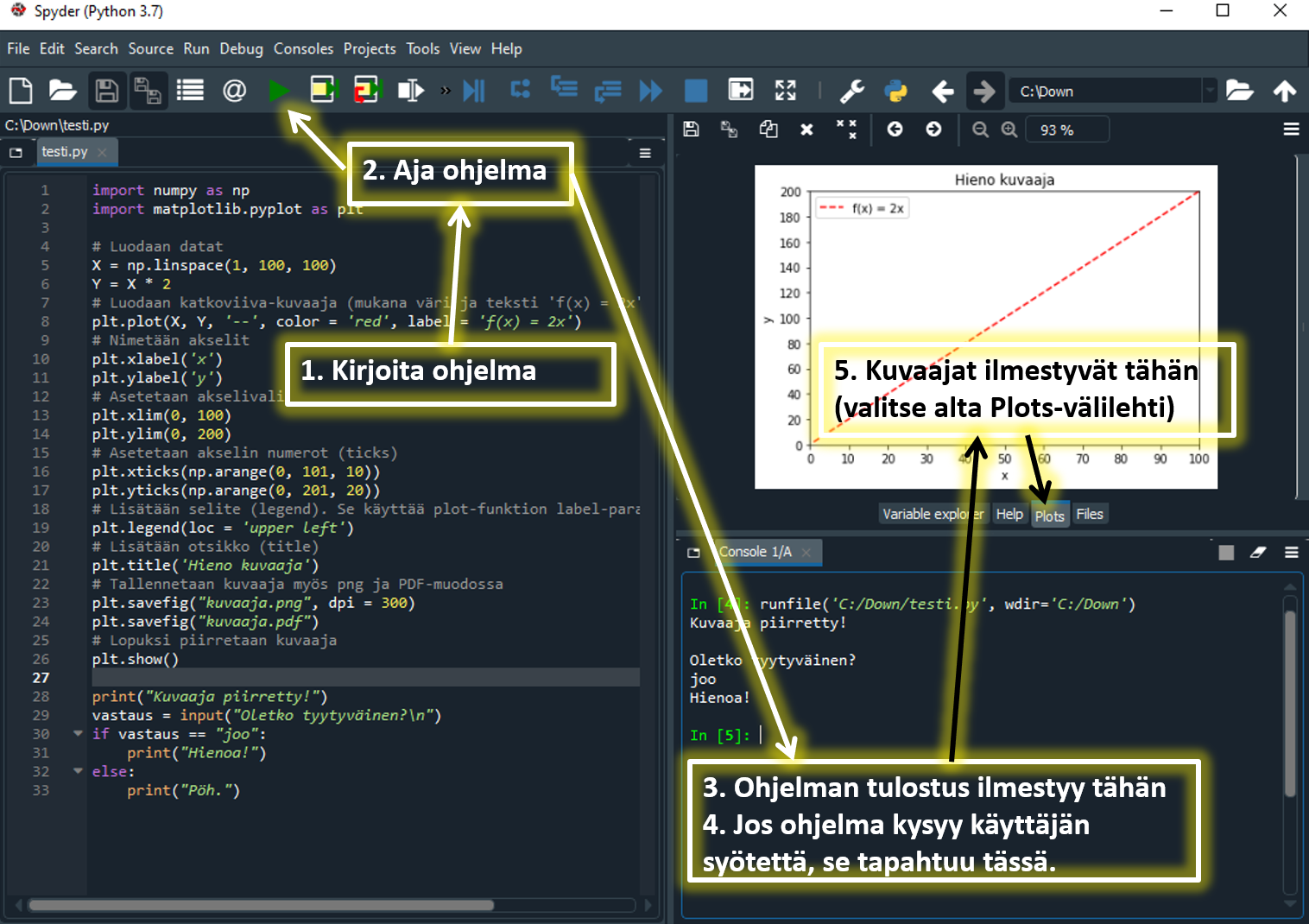
Spyderin käyttöliittymän muokkaaminen
Spyder käyttää oletuksena yllä olevissa kuvissa näkyvää tummaa värimaailmaa. Jos pidät enemmän mustasta tekstistä valkoisella taustalla, voit muuttaa värimaailman näin:
- Tools-valikko -> Preferences -> Appearance
- Interface theme -> Light
- Syntax highlighting theme -> Spyder
- Spyder käynnistyy uudelleen
Kannattaa kokeilla, kumpaa näkymää tuijottelee mieluummin.
Tiedostojen hallinnoinnista
Kun ajat kirjoittamasi ohjelman, Spyder tallentaa sen ennen ajamista (nimi.py). Kannattaa nimetä .py-tiedostot selkeästi ja lajitella ne vaikka kierroksittain
Spyderin interaktiivinen ohje
Kun viet hiiren editorin ikkunassa minkä tahansa Pythonin funktion tai avainsanan päälle, Spyder avaa pienen ohjeikkunan (tooltip). Ohjeikkunaa klikkaamalla avautuu ruudun oikealla puolella oleva Help-välilehti, josta löytyy lisätietoja haluamastasi aiheesta. Ohjeen noutaminen onnistuu myös näppäinkomennolla Ctrl+I.
CodeRunnerin testien hyödyntäminen Spyderissä
CodeRunner-ohjelmointitehtävät sisältävät erilaisia testejä, joilla kirjoittamasi ohjelma tarkastetaan. Voit myös käyttää näitä testejä Spyderissä (tai muussa kehitysympäristössä). Tämä nopeuttaa monesti virheiden etsimistä. Näin voit myös välttää miinuspisteet, joita kertyy liian monesta palautusyrityksestä.
Esimerkki
Kuvitellaan, että tehtävänä on kirjoittaa seuraavanlainen funktio:
Kirjoita funktio tiheys, joka saa parametreinä yhdisteen massan (g) ja tilavuuden (cm^3). Funktio palauttaa yhdisteen tiheyden (g/cm^3). Jos funktiota kutsutaan epäfysikaalisella parametrilla, sen pitää palauttaa arvo -1.
Kirjoitetaan määritelmän täyttävä funktio:
def tiheys(massa, tilavuus):
if massa > 0 and tilavuus > 0:
return massa/tilavuus
else:
return -1
Seuraavaksi katsotaan CodeRunnerin esimerkkitestit (Test) ja niitä vastaavat tulokset (Result):
| Test | Result |
|---|---|
| print(round(tiheys(5.0, 24.0), 2)) | 0.21 |
| print(tiheys(-1.0, 10)) | -1 |
| print(tiheys(2, 0)) | -1 |
Nyt voit käytännössä ajaa nämä testit Spyderissä omalle koodillesi kopioimalla ylläolevat testit tiheys-funktion toteutuksen alle ja ajamalla koodin:
def tiheys(massa, tilavuus):
if massa > 0 and tilavuus > 0:
return massa/tilavuus
else:
return -1
# CodeRunner-testit:
print(round(tiheys(5.0, 24.0), 2))
print(tiheys(-1.0, 10))
print(tiheys(2, 0))
Tällöin Spyderin konsoliin tulostuu:
0.21 -1 -1
Nämä arvot vastaavat Result-sarakkeen tuloksia, joten funktio on toteutettu oikein. Funktion voi nyt kopioida CodeRunneriin ja tarkistaa.
Yhteenveto
Varsinkin monimutkaisemmissa tehtävissä, joissa virheellisistä palautuksista tulee miinuspisteitä, on suositeltavaa ajaa CodeRunnerin esimerkkitestit ensin Spyderissä ja vasta sitten palauttaa koodi CodeRunneriin. Palautuksen yhteydessä esiin tulee tavallisesti lisää CodeRunner-testejä, joista osa voi epäonnistua, mutta sitten voit kopioida epäonnistuneet testit Spyderiin ja alkaa testata koodiasi näitä testejä vasten.
Virheiden etsiminen ja korjaaminen
Virheiden löytäminen ja käsittely kuuluu jokaisen ohjelmoijan perustaitoihin ja on välttämätöntä suuria ohjelmia kirjoittaessa. Tällä kurssilla ei luoda ohjelmia, jotka vaativat huomattavaa virheiden käsittelyä tai debuggaamista. Edettäessä suurempiin ohjelmiin, erityisesti graafisen käyttöliittymän sisältäviin ohjelmiin ja sekä vaativampiin (”pikkutarkkoihin”) kieliin (C, C++), on virheiden käsittely ja debuggaaminen erittäin oleellista.
Virheen löytäminen alkaa traceback-viestistä. Traceback on punainen virheilmoitus, joka kertoo syyn ohjelman kaatumiseen. Aluksi viesti voi näyttää heprealta, mutta kun sitä oppii lukemaan, se on erittäin hyödyllinen apuväline virheiden löytämisessä.
Esimerkki 1
Katsotaan ensin yksinkertaista tracebackiä, joka syntyy koodista
print(x)Traceback on:
Traceback (most recent call last):
File "C:/Users/Omistaja/Desktop/ErrorExample1.py", line 1, in <module>
print(x)
NameError: name 'x' is not defined
Tracebackin ensimmäinen rivi ilmoittaa meille virheen sijainnin. Tässä tapauksessa virhe tapahtui tiedostossa ErrorExample1.py rivillä 1. Huomaa miten virheviestissä lukee polku, jossa tiedosto sijaitsee, pelkän nimen sijaan.
Seuraava rivi kertoo meille, mitä kyseisellä rivillä lukee. Tässä tapauksessa koodin pätkä, mikä aiheuttaa virheen on print(x).
Viimeinen rivi tracebackissä kertoo meille mikä virhe on kyseessä. Kyseinen virhe on siis NameError, joka johtuu siitä, että muuttujaa x ei ole määritelty.
Esimerkki 2
Seuraava esimerkki on hieman monimutkaisempi traceback, joka on syntynyt seuraavasta koodista:
def palautaAlkio(lista, alkio):
return lista[alkio]
lista = [1, 2, 3]
print(palautaAlkio(lista,3))
Selkeyden
vuoksi jaotellaan traceback osiin:
Traceback (most recent call last): File "<ipython-input-38-055a27710ada>", line 1, in <module>< runfile('C:/Users/User/Desktop/ErrorExample.py', wdir='C:/Users/Sammako/Desktop') File "C:\Users\User\Anaconda3\lib\site-packages\spyder\utils\site\sitecustomize.py", line 705, in runfile execfile(filename, namespace) File "C:\Users\User\Anaconda3\lib\site-packages\spyder\utils\site\sitecustomize.py", line 102, in execfile exec(compile(f.read(), filename, 'exec'), namespace)
Yllä olevat viestit käsittelevät ohjelman kääntämistä, eikä niihin syvennytä tällä kurssilla.
File "C:/Users/User/Desktop/ErrorExample.py", line 5, in <module> print(palautaAlkio(lista, 3))
Jälleen
kerran tracebackistä selviää ohjelman polku, rivi, sekä rivin sisältö
File "C:/Users/User/Desktop/ErrorExample.py", line 2, in palautaAlkio
return lista[alkio]
Koska rivi, joka aiheuttaa virheen
on funktiokutsu, ilmoittaa traceback vielä erikseen virheen sijaitsevan
funktiossa nimeltä palautaAlkio, sekä rivin, jossa virhe sijaitsee sekä,
sisällön.
Tässä esimerkissä funktio, jossa virhe on, sijaitsee samassa tiedostossa kuin sen kutsu. Tapauksissa, jossa ohjelma kutsuu useita eri funktiota, useista eri tiedostoista, tämän kaltainen viesti on erittäin hyödyllinen.
IndexError: list index out of rangeVirhe on IndexError
eli ohjelma yrittää kutsua listan alkiota, jota ei ole olemassa.
On mahdollista, että virhe aiheutuu kirjastossa kuten numpy. Tällöin traceback saattaa ilmoittaa virheen sijaitsevan esim. rivillä 1000, jossain satunnaisessa tiedostossa. Tällöin täytyy etsiä viimeisin rivi tracback:ssä, joka sijaitsee itse luomassasi tiedostossa.
Esimerkki 3
Tracebackistä ei kuitenkaan aina ole apua. Otetaan esimerkiksi koodi
def kerro_kymmenella(numero): return numero * 0 numero = 5 jako = 1 / kerro_kymmenella(numero) print(jako)
Käyttäjä on luonut funktion, jonka pitäisi kertoa numero kymmenellä, mutta teki kirjoitusvirheen, minkä seurauksesta funktio palauttaa aina nollan. Kun tarkastelemme saatua tracebackiä, huomaamme ongelman olevan rivillä 6, sekä ongelman johtuvan nollalla jakamisesta.
Koska tehty virhe ei suoranaisesti aiheuta virhettä, vaan antaa väärän tuloksen, joka myöhemmin aiheuttaa virheen, ei traceback ole yhtä hyödyllinen tässä tilanteessa. On myös tilanteita, kuten graafiset käyttöliittymät, jotka eivät aina kaatuessaan luo tracebackiä. Miten siis löytää virhe, kun sen sijaintia ei tiedetä?
Virheen löytäminen
print-funktiot ovat yksinkertainen tapa löytää mahdollisia virheitä koodista. Alla oleva koodi kaatuu, mutta koska virhe on ikuinen silmukka ei traceback-viestiä synny.
numero = 5 kertoma = 1 print("testi") while numero > 1: kertoma *= numero print("testi")
Kun koodi ajetaan print-funktioiden kanssa, huomataan ensimmäisen tulostuvan, mutta toisen ei. Tästä on helppo päätellä, että virhe on while-silmukassa. Kun virheen sijainti tiedetään, on helppo huomata virheen johtuvan siitä, että muuttujan numero arvoa ei vähennetä silmukassa.
Virheiden käsittelystä kerrotaan lisää muualla oppimateriaalissa.
main-funktio
Jos olet aiemmin osallistunut kurssille CS-A1111 Ohjelmoinnin peruskurssi Y1, olet todennäköisesti tutustunut lähestymistapaan, jossa Python-ohjelmat kirjoitetaan aina main-funktion sisään. Esimerkiksi näin:
def main():
nimi = input("Anna nimesi:\n")
print("Moi", nimi)
main()
Ohjelman suoritus voisi näyttää esimerkiksi tältä:
Anna nimesi: > Karl Moi Karl
Tällä kurssilla vastaava ohjelmat kannattaa kuitenkin kirjoittaa ilman main-funktiota. Eli:
nimi = input("Anna nimesi:\n")
print("Moi", nimi)
Syynä on se, että osa CodeRunner-testeistä ei valitettavasti toimi, jos vastaus on kirjoitettu main-funktiota käyttäen.
Syventävää tietoa: Miksi main-funktiota käytetään?
Pythonissa ei siis ole pakko kirjoittaa ohjelmia main-funktiota käyttäen. Milloin main-funktiota sitten olisi syytä käyttää?
main-funktion käyttäminen on erittäin tärkeää esimerkiksi silloin, kuin kirjoitetaan moduuleja, jotka sisältävät muissa ohjelmissa käytettäviä funktioita, mutta moduuli voidaan ajaa myös omana ohjelmanaan. Tällöin on tärkeätä erottaa tilanteet, joissa jokin toinen ohjelma kutsuu moduulin funktiota tai moduuli ajetaan sellaisenaan. Otetaan esimerkki, jossa meillä on määritelty moduuli laskin (tiedosto laskin.py):
# Moduuli laskin
# Funktio tuplaa: palauttaa parametrin "luku" kaksinkertaisena
def tuplaa(luku):
return luku * 2
# main-funktio, jota ei kutsuta, jos joku tuo laskin-moduulin omaan ohjelmaansa
# import-käskyllä ja kutsuu tuplaa-funktiota
def main():
numero = int(input("Anna kokonaisluku:\n"))
tupla = tuplaa(numero)
print("Antamasi luku kaksinkertaisena on:", tupla)
# Kutsutaan main-funktiota vain, jos joku ajaa laskin-moduulin sellaisenaan
# Esimerkiksi avaa tiedoston Spyderiin ja ajaa koodin
if __name__ == "__main__":
main() Luodaan nyt ohjelma, joka hyödyntää laskin-moduulia:
import laskin
print("5 x 2 on:", tuplaa(5))
Ohjelma tulostaisi pelkästään
5 x 2 on: 10Toisaalta jos ajamme tiedoston laskin.py sellaisenaan (esimerkiksi Spyderissä), Python suorittaa laskin-moduulin main-funktion ja suoritus näyttää tältä:
Anna kokonaisluku:
> 9
Antamasi luku kaksinkertaisena on: 18 Ratkaisevan tärkeässä roolissa on siis __name__ -erikoismuuttuja, joka saa arvon "__main__", kun moduuli on ajettu omana ohjelmanaan (__ = kaksi alaviivaa peräkkäin).
Lisää yksityiskohtia aiheeseen liittyen esimerkiksi Pythonin dokumentaatiossa.
Python-oppimateriaaleja verkossa
Tältä sivulta löydät linkkejä muihin verkosta löytyviin Python-oppimateriaaleihin.
pythonprogramming.net
- Hyviä ohjeita ja paljon opetusvideoita.
- https://pythonprogramming.net/introduction-learn-python-3-tutorials/
- https://pythonprogramming.net/matplotlib-intro-tutorial/
Corey Schafer (Youtube)
- Python-opetusvideoita
- Osoite: https://www.youtube.com/playlist?list=PL-osiE80TeTt2d9bfVyTiXJA-UTHn6WwU
tutorialspoint.com
- Selkeä Python-tutoriaali
- https://www.tutorialspoint.com/python3/
docs.python.org
- Pythonin virallinen dokumentaatio
- Tutoriaali: https://docs.python.org/3/tutorial/index.html
- Kielioppi: https://docs.python.org/3/reference/index.html
pythontutor.com
- Omien Python-koodien havainnoillistaminen
- http://www.pythontutor.com/
Stackoverflow.com
- Miljoonia ohjelmointikysymyksiä ja vastauksia niihin. Kun teet englanninkielisen Google-haun, löydät usein vastauksen ongelmaasi täältä.
- http://stackoverflow.com/