8. Impedance technique

8.4. Adsorption

Many electrochemical processes include an adsorption step, which may even limit the rate of charge transfer mechanism. Let us look at a simplified theoretical situation, in which a redox pair immobilized on an electrode determines the rate of reaction alone, as illustrated in Figure 8.13.

Redox pair immobilized on the surface of an electrode.

The current density is

\displaystyle i=-nF\frac{d\Gamma_{\text{R}}}{dt}=nF\frac{d\Gamma_{\text{O}}}{dt} (8.34)

\Gamma_{\text{R}} and \Gamma_{\text{O}} are surface concentrations of reduced and oxidized species, mol cm-2.  Additionally, it is assumed that the molecules do not dissolve from the surface, but at all times it holds that  \Gamma_{\text{R}}(t)+\Gamma_{\text{O}}(t)=\Gamma_{\text{max}} . A characteristic feature of the system is that when the electrode is set to an arbitrary potential, the surface concentrations become such that the Nernst equation always holds, i.e. every steady state is an equilibrium state at the same time.

\displaystyle\left(\frac{\Gamma_{\text{O}}}{\Gamma_{\text{R}}}\right)_{eq}=\theta_{eq}=\text{exp}\left[\frac{nF}{RT}(E_{eq}-E^0)\right] (8.35)

Analogously to Equation (8.18), a linearized current-voltage equation is expressed as

\displaystyle\overline{\eta}(s)=\frac{RT}{nF}\left(\frac{\overline{i}(s)}{i_0}-\frac{\overline{\Gamma}_{\text{R}}(s)}{{\Gamma}_{\text{R},eq}}+\frac{\overline{\Gamma}_{\text{O}}(s)}{{\Gamma}_{\text{O},eq}}\right) (8.36)


The surface concentrations in the Laplace domain can be obtained directly from Equation (8.34):

  \displaystyle\overline{i}(s)=-nF(s\overline{\Gamma}_{\text{R}}(s)-\Gamma_{\text{R}, eq})=nF(s\overline{\Gamma}_{\text{O}}(s)-\Gamma_{\text{O}, eq})

 (8.37)
\displaystyle \frac{\overline{\Gamma}_{\text{R}}(s)}{{\Gamma}_{\text{R}},eq}=\frac{1}{s}-\frac{\overline{i}(s)}{nF\Gamma_{\text{R},eq}}\frac{1}{s}    ;   \displaystyle\frac{\overline{\Gamma}_{\text{O}}(s)}{{\Gamma}_{\text{O},eq}}=\frac{1}{s}+\frac{\overline{i}(s)}{nF\Gamma_{\text{O},eq}}\frac{1}{s}

(8.38)

Substitution into Equation (8.36) gives

\displaystyle Z=\frac{RT}{nFAi_0}+\frac{RT}{n^2F^2A}\left(\frac{1}{\Gamma_{\text{R},eq}}+\frac{1}{\Gamma_{\text{O},eq}}\right)\frac{1}{j\omega}=R_{ct}+\frac{1}{j\omega C}
(8.39)

The immobilized layer is modeled in impedance measurements as a combination of a resistor and capacitor in series, which is displayed as a semicircle on the admittance plot. The surface concentrations at equilibrium, \Gamma R,eq and \Gamma O,eq, can be determined using the Nernst equation and mass balance:

\displaystyle\Gamma_{\text{O,}eq}=\Gamma_{\text{max}}\frac{\theta}{1+\theta}    ;    \Gamma_{\text{R,}eq}=\Gamma_{\text{max}}\frac{1}{1+\theta}
(8.40)

Now the quantity i0 can hardly be called exchange current density because it depends on the potential:

\displaystyle i_0=nFk^0(\Gamma_{\text{R,}eq})^{1-\alpha}(\Gamma_{\text{O,}eq})^\alpha=nFk^0\Gamma_{\text{max}}\frac{\theta^\alpha}{1+\theta} (8.41)

The unit for rate constant k0 is in this case s-1. The charge transfer resistance and capacitance are expressed as

\displaystyle\ R_{ct}=\frac{RT}{n^2F^2A\Gamma_{\text{max}}k^0}\frac{1+\theta}{\theta^{\alpha}}

 (8.42)
\displaystyle\frac{1}{C}=\frac{RT}{n^2F^2A\Gamma_{\text{max}}}\frac{(1+\theta)^2}{\theta}
(8.43)

These quantities as a function of potential without the constants are shown in Figure 8.14.

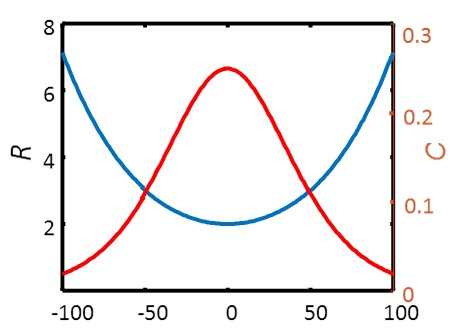
Charge transfer resistance

Figure 8.14. Charge transfer resistance and capacitance of a redox pair immobilized on an electrode, α = 0.5.

It is worth noting the high value of capacitance. A typical value for \Gamma max is 10-9 mol cm-2. If we substitute this value into the equation, the maximum capacitance becomes approximately 1 mF cm-2. The surface area of a porous material is high, and it is therefore possible to construct superconductors using immobilized redox species. The charge transfer resistance is also higher than usual. Assuming values \Gamma max = 10-9 mol cm-2 and k0 = 1 s-1, the order of magnitude of the maximum value of Rct will become 100 \Omega cm2.

Let us take a look at a model, which is a bit more realistic. In this model, a metal cation M+z is first adsorbed on the surface of the  electrode and then reduced to a metal. The current density is

\displaystyle\frac{i}{nF}=-k_c\Gamma_{\text{M}}=-k^0e^{-\alpha f(E-E^{0'})}\Gamma_{\text{M}} (8.44)

where n = z, and the subscript ’c’ of kc denotes cathode process and thus current is negative. The surface concentration of the cation \Gamma M can be expressed in terms of maximum surface concentration and surface coverage \varphi *, \Gamma M = \Gamma max \varphi . The mass balance of the adsorbed cation is

\displaystyle\frac{\partial\varphi}{\partial t}=\frac{i}{nF\Gamma_{\text{max}}}+k_ac_{\text{M}}^s(1-\varphi)-k_d\varphi=\frac{i}{nF\Gamma_{\text{max}}}+k_ac_{\text{M}}^s-(k_ac_{\text{M}}^s+k_d)\varphi (8.45)

where ka and kd are adsorption and desorption rate constants. It is therefore assumed that the adsorption is of a Langmuir type. Let us simplify the expression by ignoring concentration polarization and keeping solution concentration, c_{\text{M}}^s=c_0 , constant, which means that adsorption is the rate-limiting step. At a steady state, \partial\varphi/\partial t=0 , and therefore

\displaystyle\varphi_{ss}=\frac{i_{ss}/nF\Gamma_{\text{max}}+k_ac_0}{k_ac_0+k_d} (8.46)

The subscript ’ss’ denotes steady state. Linearizing Equation (8.44) and transforming it to the Laplace domain gives

\displaystyle\frac{\Delta\overline{i}(s)}{nF}=-k_c\Gamma_{\text{max}}(\Delta\overline\varphi(s)-\alpha f\varphi_{ss}\Delta\overline{E}(s)) (8.47)

Equation (8.45) is linear to begin with, so after Laplace transformation we have

  \displaystyle s\Delta\overline{\varphi}(s)=\frac{\Delta\overline{i}(s)}{nF\Gamma_{\text{max}}}+\frac{k_ac_0}{s}-(k_ac_0+k_d)\Delta\overline\varphi(s)

 (8.48)
\displaystyle \Rightarrow \Delta\overline{\varphi}(s)=\frac{\Delta\overline{i}(s)}{nF\Gamma_{\text{max}}(s+k_ac_0+k_d)}+\frac{k_ac_0}{s(s+k_ac_0+k_d)}

(8.49)
The second term on the right-hand side of Equation (8.49) is non-periodical because it contains neither \Delta\overline{i}(s) nor  \Delta\overline{E}(s) . We leave it out and insert the first term into Equation (8.47), replace s with j\omega and divide both sides by current. As a result, we find

\displaystyle\frac{1}{nFA\Gamma_{\text{max}}}=-k_c\left(\frac{1}{nFA\Gamma_{\text{max}}(j\omega+k_ac_0+k_d)}-\frac{\alpha nF}{RT}\varphi_{ss}Z\right) (8.50)

Simplifying the expression gives

\displaystyle Z=\frac{RT}{\alpha n^2F^2A\Gamma_{\text{max}}\varphi_{ss}}\left[\frac{1}{k_c}+\frac{1}{j\omega+k_ac_0+k_d}\right] (8.51)


The first term of Equation (8.51) is not dependent on frequency, and thus it represents the charge transfer resistance. The second term is a combination of two elements, and after giving it some thought, it becomes evident that the term represents the parallel combination of a capacitor and a resistor. The equivalence circuit becomes complete when the double layer capacitance, which is always present, is added in parallel with this faradaic impedance, and we obtain the equivalent circuit and impedance plot displayed in Figure 8.15.

Equivalent circuit and impedance plot for an electrode reaction with an adsorption step.

Figure 8.15. Equivalent circuit and impedance plot for an electrode reaction with an adsorption step.

 

Substituting jss into Equation (8.51), which we obtain using Equations (8.44) and (8.46):

\displaystyle\varphi_{ss}=\frac{k_ac_0}{k_ac_0+k_d+k_c} (8.51)

Let us find the final expressions for Rct, Rads and Cads:

\displaystyle R_{ct}=\frac{RT}{\alpha n^2F^2A\Gamma_{\text{max}}k_ac_0}\left(1+\frac{k_ac_0+k_d}{k_c}\right)

(8.52)
\displaystyle R_{ads}=\frac{RT}{\alpha n^2F^2A\Gamma_{\text{max}}k_ac_0}\left(1+\frac{k_c}{k_ac_0+k_d}\right)

(8.53)
\displaystyle C_{ads}=\frac{\alpha n^2F^2A\Gamma_{\text{max}}k_ac_0}{RT(k_ac_0+k_d+k_c)}
(8.54)


Values for physical parameters can be determined as follows:

  \displaystyle\frac{R_{ct}}{R_{ads}}=\frac{k_ac_0+k_d}{k_c}

 (8.55)
  \displaystyle R_{ads}C_{ads}=\frac{1}{k_ac_0+k_d}

 (8.56)
\displaystyle R_{ct}C_{ads}=1/k_c (8.57)

The impedance method therefore gives the value of the electrochemical rate constant explicitly, but finding the values of adsorption and desorption constants requires measurements at varying solution concentrations c0.
We have now shown that adsorption is observed as capacitance in impedance measurements. The derivation of impedance for more complicated mechanisms is, in principle, as simple as this; the only difference is that the mathematical treatment required is more extensive. The study of more complicated mechanisms is outside of the scope of this book. However, it is worth noting that even the previous example would be hopelessly difficult to study using other transient methods, and an analytical solution to the problem would not be possible.

 


* The symbol for surface coverage is usually \theta , but we have already reserved it for the quantity exp[(nF)/(RT)(E - E0’)].