2. Thermodynamics of electrolyte solutions

2.4. Solvent-ion interaction

Melting points of common salts are very high because the ions in the lattice are bound together with very strong electrostatic forces. They can dissolve, however, in polar solvents at rather high concentrations. The reason for this is the ability of the solvent molecules to solvate, i.e. to gather around ions, mainly using electrostatic forces. In the case of water, we talk about hydration and hydration number that is the number of water molecules bound by salt. For LiCl, the hydration number is 7, NaCl 3.5 and MgCl2 14. The hydration number is often assigned to the cation.

Free energies of hydration are negative and rather large, of the order of -300 to -4000 kJ/mol, which reflects the strength of the interactions between ions and water. The solubility of salts decreases with the relative permittivity, i.e. the polarity of the solvent, and in non-polar solvents common salts practically do not dissolve at all.

The interaction between a solvent and an ion is traditionally estimated with the Born model that, despite being very simple, gives a good picture of the electrostatics of solvation. In addition to the electrostatic interaction, there are also other forces between ions and solvents that are addressed in, for example, the scaled particle theory [1].

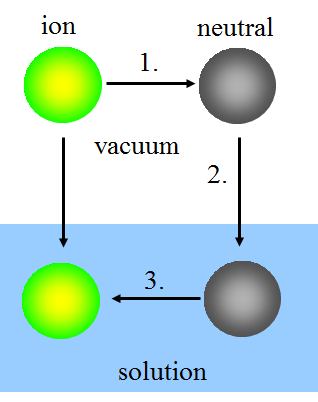
Born model.

Figure 2.1. Born model.

In the Born model, ion solvatation is thought to take place in three steps:

1. Uncharging the ion in vacuum.

2. Bringing the neutral species into the solution.

3. Charging the species in the solution.

The work to charge a species in vacuum is (a = ion radius)

\displaystyle w= \int_{0}^{ze}{V(q)dq}=\int_{0}^{ze}{V \frac{qdq}{4\pi\ \varepsilon _0a}}= \frac{z^2e^2}{8\pi\varepsilon_0a} , (2.25)

Hence, the work Step 1 has an opposite sign to this. Charging a species in the solution has the work, accordingly
\displaystyle w_3= \frac{z^2e^2}{8\pi\varepsilon_0\varepsilon_ra} (2.26)

The electrostatic energy of ion solvation (IS) is therefore

\displaystyle w_{\text{el}}= \Delta G_{\text{IS}}=- \frac{z^2e^2}{8\pi\varepsilon_0a} \left( 1-\frac{1}{\varepsilon_r}\right) (2.27)

The work (energy) of Step 2 > 0, because a cavity must be formed for a species in the solution. This work is ~(4/3)πa3P where P is pressure. When a species is brought through the solution surface, work must be done against the surface tension \gamma ; that work is 4\pi a^2\gamma .

The electrostatic energy is, however, so dominating and negative that solvation is a spontaneous process. Assume that a = 0.1 nm, z = 1 εr = 78.4, p = 1 atm ja γ = 0.0728 J/m2. The electrostatic energy is now -7.1 eV = -684 kJ/mol, while Step 2 has energy of only 0.057 eV = 5.5 kJ/mol. Although there are other forces in Step 2, we are no longer concerned with them.

If an ion is partitioned between an aqueous and an organic solution, Equation (2.27) can be applied via a thought process where an ion is brought from a vacuum into the both phases. The difference between the solvation energies becomes

\displaystyle w_{\text{el}}= \Delta_o^wG=\pm\frac{z^2e^2}{8\pi\varepsilon_0a} \left( \frac{1}{\varepsilon_r^w} -\frac{1}{\epsilon_r^{o}}\right) (2.28)

From Equation (2.11) we see that  ( \frac{\partial \Delta G}{\partial T})_{p,\mu_i}=-\Delta S The entropy of solvation is therefore
\displaystyle \Delta S_{\text{IS}}=- \frac{z^2e^2}{8\pi\varepsilon_0a} \frac{1}{\varepsilon_r^2} \left( \frac{\partial\varepsilon_r}{\partial T}\right) (2.29)

Since \Delta G=\Delta H-T\Delta S ,

\displaystyle\Delta H_{\text{IS}}=- \frac{z^2e^2}{8\pi\varepsilon_0a} \left( 1-\frac{1}{\varepsilon_r}- \frac{T}{\varepsilon_r^2} \frac{\partial \varepsilon_r}{\partial T}\right) (2.30)

For water (∂er/∂T) = -0.3595, giving the enthalpy share of \Delta G_{IS} -7.2 eV and the entropy share  -T\Delta S_{IS}  = +0.1 eV at room temperature. The entropy of solvation therefore increases as a result of issues that are beyond electrostatics. Upon solvation, the solvent molecules are organized around an ion in a configuration that is different from that in the bulk of the solution, reducing the entropy of the solution. These issues are beyond the scope of this book. An interested reader can look at the text book by Y. Marcus [2].

Table 2.1. Standard Gibbs free energy, enthalpy and entropy of ion hydration and the molar volume in water for selected ions. From: Y. Marcus in, A.G. Volkov and D.W. Deamer (Eds.), Liquid/liquid interfaces. Theory and methods, CRC Press, Boca Raton, 1996. With the Publisher’s (CRC Press) permission.

 

 

 

 

 

 

 

 

 

Cations

Radius/pm

\Delta G_{hyd}^\theta

/kJ mol-1

\Delta H_{hyd}^\theta

/kJ mol-1

\Delta S_{hyd}^\theta

/J mol-1 K-1

\bar V_m^\theta

/cm3 mol-1

 

 

H+

 

-1055

-1090

-131

-5.5

 

 

Li+

69

-475

-530

-161

-6.4

 

 

Na+

102

-365

-415

-130

-6.7

 

 

K+

138

-295

-330

-93

3.5

 

 

Rb+

149

-275

-305

-84

8.6

 

 

Cs+

170

-250

-280

-78

15.8

 

 

NH4+

148

-285

-325

-131

12.4

 

 

Me4N+

280

-160

-215

-163

84.1

 

 

Et4N+

337

-130

-205

-241

143.6

 

 

Mg2+

72

-1830

-1945

-350

-32.2

 

 

Ca2+

100

-1505

-1600

-271

-28.9

 

 

Fe2+

78

-1840

-1970

-381

-30.2

 

 

Ni2+

69

-1980

-2115

-370

-35

 

 

Fe3+

65

-4265

-4460

-576

-53

 

 

 

 

 

 

 

 

 

 

Anions

 

 

 

 

 

 

 

F–

133

-465

-510

-156

4.3

 

 

Cl–

181

-340

-365

-94

23.3

 

 

Br–

196

-315

-335

-78

30.2

 

 

I–

220

-275

-290

-55

41.7

 

 

OH–

133

-430

-520

-180

-0.2

 

 

NO3–

179

-300

-310

-95

34.5

 

 

ClO4–

250

-205

-245

-76

49.6

 

 

 

 

 

 

 

 

 

 

 


[1] A review of the theory is provided by R.A. Pierotti, Chem. Rev. 76 (1976) 717-726.

[2] Y. Marcus, Ion Solvation, Wiley, 1985.