5. Electrical double layer and adsorption

5.4. Effect of inner layer on capacitance

As shown in Figure 5.1, the surface of an electrode includes an inner and an outer Helmholtz layer, which may have a net charge. In the mathematical treatment of the diffuse double layer, \phi 0 must be replaced by \phi 2 and x by  x-x_2 in the previous equations; keep in mind that x2 is the distance between the outer Helmholtz plane and the electrode, and \phi 2 = \phi (x2). From now on, we will treat the Helmholtz layers as one and call this the inner layer.

Continuity of electric flux is one of the central laws of electrostatics. According to it, at the phase boundary \alpha | \beta , we have

\displaystyle\varepsilon_r^{\alpha}\varepsilon_0\left(\frac{\partial\phi^{\alpha}}{\partial x}\right)-\varepsilon_r^{\beta}\varepsilon_0\left(\frac{\partial\phi^{\beta}}{\partial x}\right)=q (5.52)


Superscripts \alpha and \beta in Equation (5.52) denote the respective phases, and q is the charge density of the phase boundary. If q is zero, and \varepsilon_r^{\alpha}=\varepsilon_r^{\beta} , the continuity condition of electric flux means that the electric field is continuous.

Assume that the charge of the inner layer is zero. It follows that the potential profile, according to the Poisson equation, is linear: 

\displaystyle \left(\frac{\partial\phi}{\partial x}\right)_{\text{inner layer}}=\frac{\phi_2-\phi_0}{x_2}                                        (5.53)


Because of the partial loss of degrees of freedom of the water molecules in the inner layer, its relative permittivity is low compared to that of the bulk solution. Based on Equations (5.42), (5.48) and (5.52), the continuity condition of the electric flux density between the layers at the boundary at x = x2 for a symmetrical z:z electrolyte becomes

\displaystyle\sigma^m=-\varepsilon_r\varepsilon_0\frac{\phi_2-\phi_0}{x_2} =(8RTc^b\varepsilon_r^b\varepsilon_0)^{1/2}\sinh\left(\frac{zF\phi_0}{2RT}\right) (5.54)

where \varepsilon r is the relative permittivity of the inner layer, and \varepsilon rb   that of the bulk solution. We can now solve this for \phi 2:

\displaystyle \phi_2=\phi_0-\frac{\sigma^mx_2}{\varepsilon_r\varepsilon_0} (5.55)

Substituting \phi 2 into Equation (5.54) and taking the derivative with respect to \phi 0 results, after some algebra, in the total capacitance of the electrode, CT:

\displaystyle\frac{1}{C_{\text{T}}}=\left(\frac{\partial\sigma^m}{\partial\phi_0}\right)^{-1}=\frac{x_2}{\varepsilon_r\varepsilon_0}+\frac{1}{(2\varepsilon_r^b\varepsilon_0z^2F^2c_b/RT)\cosh(zF\phi_2/2RT)}=\frac{1}{C_2}+\frac{1}{C_d} (5.56)


Equation (5.56) states that the total capacitance is made up of two components, the series combination of the inner layer and the diffuse layer. [1] The capacitance of the inner layer C2 is independent of potential:

\displaystyle C_2=\frac{\varepsilon_r\varepsilon_0}{x_2} (5.57)

Because C2 » Cd, Cd dominates the total capacitance. The analysis can even be taken a step further: The charge of the electrode \sigma m in Equation (5.32) can be solved by integration:

\displaystyle \sigma^m=\int_{E_{pzc}}^E {C_ddE}

(5.58)


where Epzc is the potential of zero charge of the electrode, in other words, the potential at which  \sigma m = 0. The potential of zero charge is usually taken to be the potential at which the capacitance of the electrode is at the minimum. Without specific adsorption, i.e. the charge of the inner layer, Epzc ≈ E0'. The non-zero minimum of capacitance is therefore considered to be the first signal of specific adsorption. The integral (5.58) must be solved numerically from the experimental capacitance curve because its mathematical form is not known.

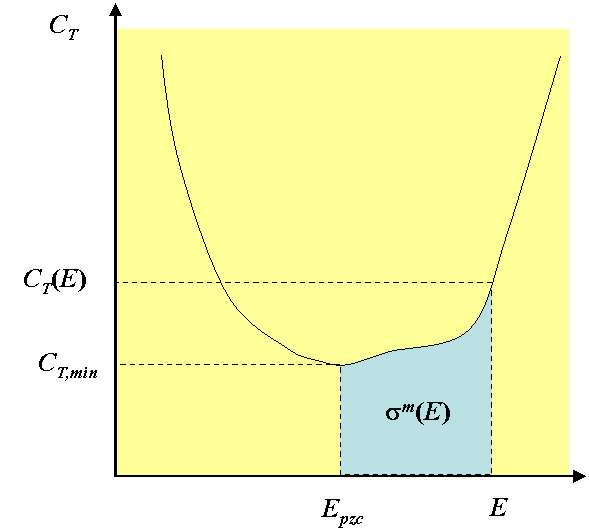
Determination of the electrode charge from the experimental capacitance curve.

Figure 5.6. Determination of the electrode charge from the experimental capacitance curve.
 

 

Typically, however, there are specifically adsorbed ions on the electrode. In this case, the charge of the electrode \sigma m is compensated for the charge of the inner layer q' and the charge of the diffuse layer qd:

\displaystyle \sigma^m=q'+q_d (5.59)


----

[1] In parallel combination, the values of capacitance are added, and in series, the reciprocals of the values, see Chapter 9.

[2] If \varepsilon r ≈ 5 and x2 ≈ 1 nm, C2 ≈ 44 mFcm-2, whereas Cd is typically of the order of magnitude 0.1...1 mFcm-2.










You can now test your conceptual knowledge by taking Quiz Chapter 5.