CHEM-E4106 - Electrochemistry D, Lecture, 9.1.2023-21.2.2023
This course space end date is set to 21.04.2023 Search Courses: CHEM-E4106
Kirja
7. Electrochemical methods
7.1. Transient methods
The analysis of all transient methods starts from Fick’s second law, Equation (3.54) and the boundary condition (3.48). We only consider a trace ion in a one-dimensional, semi-infinite space x ≥ 0. The Fick’s 2nd law is first converted into the Laplace domain:
 |
(7.1) |
|---|
where the upper bar denotes a variable in the
Laplace domain;  is the initial or the bulk concentration of ion i, and s is the Laplace variable*.
The general solution of this ordinary differential equation is
is the initial or the bulk concentration of ion i, and s is the Laplace variable*.
The general solution of this ordinary differential equation is
 |
(7.2) |
|---|
A(s) and B(s) are constants that are determined from the boundary conditions. In order to keep the concentration finite when x → ∞, B(s) must be zero. Boundary condition (3.48) gives:
 |
(7.3) |
|---|
 |
(7.4) |
|---|
Equation (7.4) is completely general as it was derived without assumptions related to any particular method. In order to proceed, we have to define the experimental method.
7.1.1 Potential step
In the potential step method, the electrode potential is stepped at t = 0 to a new value and then kept constant. If the reaction is reversible, the surface concentrations of the redox couple obey the Nernst equation:
![\displaystyle\left(\frac{c_{\text{o}}}{c_{\text{R}}}\right)_0=\text{exp}\left[\frac{nF}{RT}(E-E^{0'})\right]= \theta=\text{constant} \displaystyle\left(\frac{c_{\text{o}}}{c_{\text{R}}}\right)_0=\text{exp}\left[\frac{nF}{RT}(E-E^{0'})\right]= \theta=\text{constant}](https://mycourses.aalto.fi/filter/tex/pix.php/31eff04a5cc89fd6326a43fa32d881df.gif) |
(7.5) |
|---|
 |
(7.6) |
|---|
Let us assume that we initially only have reduced species R present and the potential step is made in the anodic direction, i > 0, whereby cR at the electrode surface is lowered due to its oxidation. Hence
 |
(7.7) |
|---|
 |
(7.8) |
|---|
because  . Using Equation (7.6) current
density
. Using Equation (7.6) current
density  can be solved:
can be solved:
 |
(7.9) |
|---|
Current density in the time domain is obtained by an inverse transformation that can be found in the Table of Laplace transforms (Appendix 5):
 |
(7.10) |
|---|
If the potential is
stepped to such high anodic potential  that the surface concentration of R immediately drops to zero, we see directly
from Equation (7.7) that
that the surface concentration of R immediately drops to zero, we see directly
from Equation (7.7) that
 |
(7.11) |
|---|
Equation (7.11) is known
as the Cottrell equation, which states
that, along with Equation (7.10), current under diffusion control decays in a manner proportional
to t−1/2. These equations
bear the peculiarity that at time t =
0 current should be infinite. This naturally never happens because a small solution resistance Rs always remains between the electrode and the Luggin capillary (see Chapter 4). Current at t = 0 is therefore equal to  where
where  is the height of the potential step. Electrodes
also always have double layer capacitance, Cdl,
and charging this capacitance makes current decay exponentially,
is the height of the potential step. Electrodes
also always have double layer capacitance, Cdl,
and charging this capacitance makes current decay exponentially,  . Total current is the sum of this charging current, ic, and diffusion current,
Equation (7.10) or (7.11). Charging time is, however, very short on solid
electrodes, only a few microseconds, and usually we do not notice it at all.
. Total current is the sum of this charging current, ic, and diffusion current,
Equation (7.10) or (7.11). Charging time is, however, very short on solid
electrodes, only a few microseconds, and usually we do not notice it at all.
The current from Equation (7.10) can be written in terms of the Cottrell current, Equation (7.11):
 |
(7.12) |
|---|
Solving for
 gives
gives |
(7.13) |
|---|
Taking the logarithm and using the definition of
 , Equation (7.5), we end
up with the result
, Equation (7.5), we end
up with the result |
(7.14) |
|---|
When current  , the final term of this equation vanishes and we have reached
the half-wave potential E1/2:
, the final term of this equation vanishes and we have reached
the half-wave potential E1/2:
 |
(7.15) |
|---|
If an electrode reaction has a limited rate, the Nernst equation (7.5) cannot be used as the boundary condition, but Equation (6.12) is used instead. In the Laplace domain it reads
 |
(7.18) |
|---|
where kox and kred are the rate constants of the oxidation and reduction reactions, respectively, as discussed in the previous chapter. Inserting the surface concentrations, Equations (7.7) and (7.8), into this equation, current density takes on the following form:
 |
(7.19) |
|---|
Equation (7.19) is of the
form  for which the inverse
transform is found tabulated:
for which the inverse
transform is found tabulated:
 |
(7.20) |
|---|
When
 ,21F† making current density at t = 0 equal to
,21F† making current density at t = 0 equal to  . Since all reactions have a limited rate (value of the rate constant), the formal singularity
in the Cotrell equation cannot exist in reality. The graph of Equation (7.20) approaches
the time dependence t-1/2 at longer times, i.e. diffusion always steps
in to limit the current (see Figure 7.2).
. Since all reactions have a limited rate (value of the rate constant), the formal singularity
in the Cotrell equation cannot exist in reality. The graph of Equation (7.20) approaches
the time dependence t-1/2 at longer times, i.e. diffusion always steps
in to limit the current (see Figure 7.2).
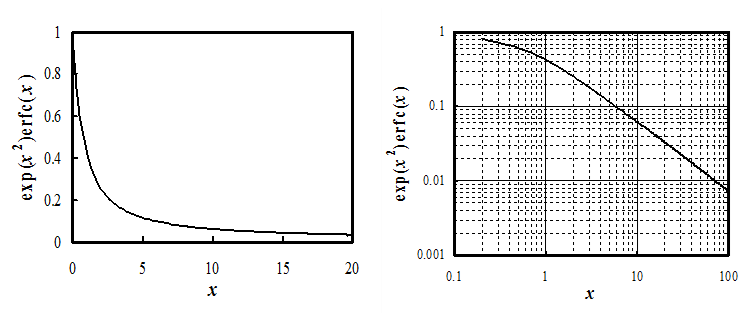
At low values of x the function can be linearized, and current density is given by:
 |
(7.21) |
|---|
Plotting current density
as a function of  and extrapolating to
zero, the intercept at the current axis gives the value of kox. In principle, this could be seen directly from current
at t = 0, but this value may be
blurred due to the charging current or the limited response time of the
potentiostat.
and extrapolating to
zero, the intercept at the current axis gives the value of kox. In principle, this could be seen directly from current
at t = 0, but this value may be
blurred due to the charging current or the limited response time of the
potentiostat.
Potential steps are mainly used to determine electrochemical rate constants, as indicated above. In systems in which an electrode reaction is accompanied by a homogeneous reaction, a second step to the reverse potential can be made. The response to the second step now depends on the rate of the homogeneous reactions, which can be utilized in the analysis; these problems are beyond the scope of this book.
7.1.2 Linear potential scan or cyclic voltammetry
Linear potential scan or cyclic voltammetry is probably the most commonly applied electrochemical method. Although its calculus is more complicated than that of a potential step above, and although the accurate determination of kinetic parameters is prone to errors from various sources, it is an excellent semi-quantitative method. With reasonable training and experience, it is easy to deduce what kind of phenomena will prevail in the system. Estimates of the electrode reaction rate and the number of electrons exchanged are readily available, and the presence of an adsorption step or a following homogeneous reaction can easily be detected, for example. More specific reaction mechanisms, such as disproportionation also have their own very characteristic responses. The analysis of an electrochemical system is therefore commonly initiated with potential scans at varying scan rates, after which a more specific method can be chosen that applies to that particular problem.
As the name tells, the
electrode potential is scanned linearly as a function of time. If the scan is
reversed immediately from the end value back to the initial potential, the
procedure is called cyclic voltammetry. The scan rate is usually kept the same
in the forward and backward scans, although this is not mandatory; the theory of
cyclic voltammetry has been developed for constant scan rates. The potential
function in cyclic voltammetry can formally be written as
 |
(7.22) |
|---|
where Ei is the initial potential, v the scan rate (
 ), and ts the time
of the scan reversal; the corresponding potential is accordingly Es (’s’ = switching). The scan rate v
can be either positive or negative.
), and ts the time
of the scan reversal; the corresponding potential is accordingly Es (’s’ = switching). The scan rate v
can be either positive or negative.  is the Heaviside step function
that has the value zero when t < ts and unity when
is the Heaviside step function
that has the value zero when t < ts and unity when  .
.Because the quantity  in Equation (7.5) is no more constant, the
Nernst equation cannot be transformed to the Laplace domain (Equation (7.6)). Instead,
the boundary condition is written as
in Equation (7.5) is no more constant, the
Nernst equation cannot be transformed to the Laplace domain (Equation (7.6)). Instead,
the boundary condition is written as
 |
(7.23) |
|---|
where
![\theta _i=\text{exp}[\frac{nF}{RT}(E_i-E^{0'})]] \theta _i=\text{exp}[\frac{nF}{RT}(E_i-E^{0'})]]](https://mycourses.aalto.fi/filter/tex/pix.php/ca0928086a19cdd2552a9eabf202a697.gif) and
and  ;
;  has the dimension s−1.
The surface concentrations, Equation (7.4), are transformed back to the time
domain using the convolution theorem:
has the dimension s−1.
The surface concentrations, Equation (7.4), are transformed back to the time
domain using the convolution theorem: |
(7.24) |
|---|
 |
(7.25) |
|---|
In the above
equations, u is the dummy time
variable. Inserting Equations (7.24) and (7.25) into Equation (7.23) we find that
 |
(7.26) |
|---|
 is defined earlier. The problem is reduced to
the solution of the convolution integral on the left-hand side where the
current function resides. In addition, the integral has a singularity at the
upper integration limit. Equation (7.26) is written in a dimensionless form for
the numeric solution. The time variable u
is replaced with a dimensionless potential variable
is defined earlier. The problem is reduced to
the solution of the convolution integral on the left-hand side where the
current function resides. In addition, the integral has a singularity at the
upper integration limit. Equation (7.26) is written in a dimensionless form for
the numeric solution. The time variable u
is replaced with a dimensionless potential variable  , leading to
, leading to  . The current function i(u) is formally replaced
with a new function
. The current function i(u) is formally replaced
with a new function  . The convolution integral is now in the form
of
. The convolution integral is now in the form
of
 |
(7.27) |
|---|
This is further divided by
 , resulting in the dimensionless current function
, resulting in the dimensionless current function  :
:
 |
(7.28) |
|---|
where  . The real physical current (density) is expressed by the
dimensionless current (density) as
. The real physical current (density) is expressed by the
dimensionless current (density) as
 |
(7.29) |
|---|
If only species ‘R’ is initially present,
 is replaced with
is replaced with  , Cr = 1,
and unity vanishes from the numerator of the right hand side of Equation (7.28).
, Cr = 1,
and unity vanishes from the numerator of the right hand side of Equation (7.28).Integral equation (7.28) must be solved numerically. The best known methods is that of Nicholson and Shain in 1964 [1]. Integration by parts removes the singularity at the upper limit:
The
first term on the right-hand side vanishes at the upper limit, and because the
experiments are initiated at the potential where current is zero, it also vanishes at the lower limit. The second term is replaced with a sum, dividing
Equation
(7.31) thus assumes that in the interval [k,
k+1] the term
|
|---|
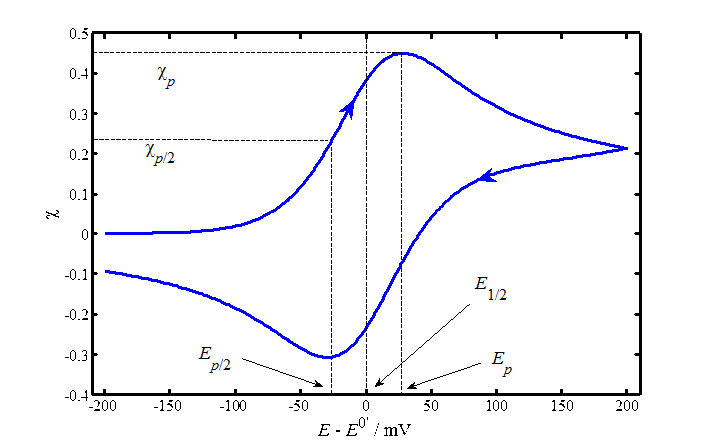
The numeric solution of the convolution integral gives the following diagnostic criteria for a reversible reaction:
1. The peak current density, ip, is
 |
(7.33) |
|---|
Equation
(7.33) is known as the Randles-Sevcík
equation. It is most often used to determine the diffusion coefficient of a
trace ion by plotting peak currents as the function of  . Alternatively,
if the diffusion coefficient is known, the concentration can be calculated.
. Alternatively,
if the diffusion coefficient is known, the concentration can be calculated.
2. The potential of the peak current, Ep, is related to the half-wave potential, E1/2, with
 |
(7.34) |
|---|
 mV at 25 ºC mV at 25 ºC |
(7.35) |
|---|
Ep/2 is the potential at which current is half of the peak current; finding this potential from a graph is easier than Ep because the current peak may be rather flat.
3. The
separation between the current peaks in forward and reverse directions,  , is 59/n
mV at 25 ºC; this is the diagnostic
criterion for the reversibility of an electrochemical reaction.
, is 59/n
mV at 25 ºC; this is the diagnostic
criterion for the reversibility of an electrochemical reaction.
4. The mid-point of the potentials of the peak currents is ~E1/2.
If an electrode reaction has a limited rate, the Nernst equation is replaced by the kinetic equation (6.12)
into which the surface concentrations, Equations (7.24) and (7.25) are added. Potential
is now included in the rate constants kox
and kred, Equation (6.10).
The numeric solution is rather cumbersome, so we will only present the results. The sluggishness of an
electrode reaction is seen as an increase of  as the function of the scan rate and as a decrease of the peak currents.
Table 7.1 shows n
as the function of the scan rate and as a decrease of the peak currents.
Table 7.1 shows n as the function of the dimensionless parameter
as the function of the dimensionless parameter  .
.
 |
(7.37) |
|---|
 and
and  are defined in Chapter 6, and
are defined in Chapter 6, and  and
and  are as above.
are as above.
As Table 7.1 shows, the
peak separation  is practically the same as in the reversible
case when
is practically the same as in the reversible
case when  > 20. A typical value of a diffusion
coefficient is of the order of 10-5 cm2 s-1, and since the scan rate cannot be increased without limits – for
technical reasons 1 V s−1 often is the upper limit – the upper limit
of k0 that can be
determined with cyclic voltammetry is of the order of 0.5-1 cm s−1.
The accuracy of the analysis based on Table 7.1 is not very good at higher
values of
> 20. A typical value of a diffusion
coefficient is of the order of 10-5 cm2 s-1, and since the scan rate cannot be increased without limits – for
technical reasons 1 V s−1 often is the upper limit – the upper limit
of k0 that can be
determined with cyclic voltammetry is of the order of 0.5-1 cm s−1.
The accuracy of the analysis based on Table 7.1 is not very good at higher
values of  : When
: When  decreases from 20 to 5,
decreases from 20 to 5,  increases only 4 mV, which is the level of measurement accuracy due to the flatness of the current peaks. Yet cyclic
voltammetry is an excellent preliminary method because if we see, for example,
that the peak separation increases with the scan rate, we know that the
electrode reaction is under kinetic control and we get an estimate for the value
of k0. Other techniques such as potential step or impedance
spectroscopy can then be used for more accurate determination.
increases only 4 mV, which is the level of measurement accuracy due to the flatness of the current peaks. Yet cyclic
voltammetry is an excellent preliminary method because if we see, for example,
that the peak separation increases with the scan rate, we know that the
electrode reaction is under kinetic control and we get an estimate for the value
of k0. Other techniques such as potential step or impedance
spectroscopy can then be used for more accurate determination.
|
Table 7.1. Peak separation as a function of
parameter |
|
|
20 |
61 |
|
7 |
63 |
|
6 |
64 |
|
5 |
65 |
|
4 |
66 |
|
3 |
68 |
|
2 |
72 |
|
1 |
84 |
|
0.75 |
92 |
|
0.50 |
105 |
|
0.35 |
121 |
|
0.25 |
141 |
|
0.10 |
212 |
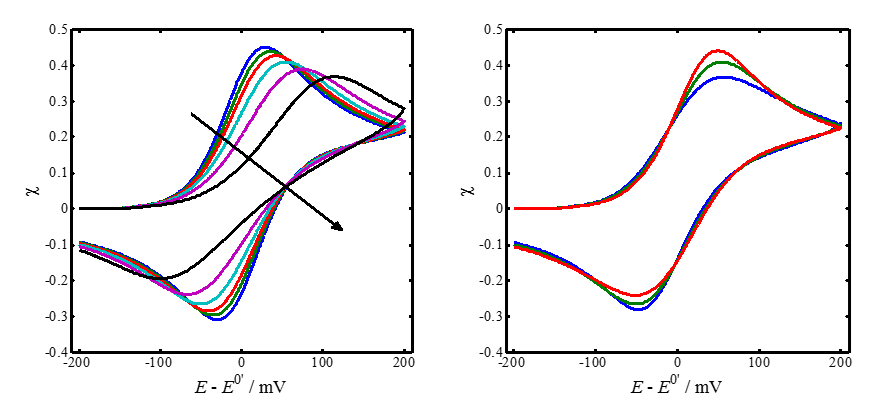
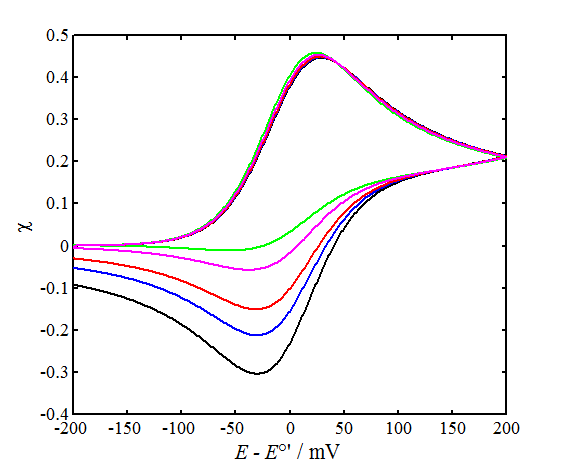
The left-hand panel of Figure 7.5 shows a few simulated
voltammograms with varying values of parameter  ,
keeping the scan limits and
,
keeping the scan limits and  constant. The peak
separation
constant. The peak
separation  does not quite correspond to Table 7.1 because
the smaller
does not quite correspond to Table 7.1 because
the smaller  is, the more sensitive is
is, the more sensitive is  to the switching potential where the scan
direction is reversed.
to the switching potential where the scan
direction is reversed.
In the right panel, parameter  is kept constant and the value of the charge
transfer coefficient
is kept constant and the value of the charge
transfer coefficient  is varied. As can be
seen, the effect of
is varied. As can be
seen, the effect of  on the shape of the
voltammograms is rather small. Increasing
on the shape of the
voltammograms is rather small. Increasing  increases the oxidation current peak and decreases the reduction current peak.
Marcus theory showed that a is not a constant but
varies slightly as the function of potential. The value
0.5 is therefore most commonly assumed to be
increases the oxidation current peak and decreases the reduction current peak.
Marcus theory showed that a is not a constant but
varies slightly as the function of potential. The value
0.5 is therefore most commonly assumed to be  , which is quite an accurate assumption around the half-wave potential.
, which is quite an accurate assumption around the half-wave potential.
 |
|---|
|
Solving more complex reaction mechanisms is easier with
numerical simulations of the transport equations. Let us consider an EC mechanism
where R is first oxidized to O, which then reacts homogeneously further to P:
Let us assume that the electrochemical reaction is reversible and the homogeneous reaction is irreversible, with a rate constant of k. The transport equations are:
The equations
above are converted into a dimensionless form with the following change of
variables:
The continuity equation on the electrode becomes
The relationship between I(T) and c is easy to calculate when the scan limits, Ei and Es, are known. Equations (7.41) - (7.43) can be solved using various numerical methods.‡ A simulation with varying values of K can be found below
Figure 7.6 shows the characteristics of the EC mechanism:
when the rate of the homogeneous reaction increases or the scan rate decreases, the
reverse current vanishes because the oxidized species ‘O’ formed in the
electrochemical step reacts further to ’P’ to a greater extent, thereby decreasing
the concentration of ‘O’. Hence by measuring the reverse current peak at
varying scan rates, K can be
determined using a simulated working
curve. Such a working curve can represent, for example, the ratio of the
current peaks as a function of K[3].
|
|---|
If the peak separation  is less than 59/n mV, the
electrode reaction is probably linked to an adsorption step. If adsorption
is the rate-limiting step, the oxidation and reduction current peaks can be found at
the same potential and are directly proportional to the scan rate, not to the
square root of the scan rate like under diffusion control.
is less than 59/n mV, the
electrode reaction is probably linked to an adsorption step. If adsorption
is the rate-limiting step, the oxidation and reduction current peaks can be found at
the same potential and are directly proportional to the scan rate, not to the
square root of the scan rate like under diffusion control.
Electrode capacitance Cdl also contributes to the measured current. The capacitive (charging) current, iC, is
 |
(7.44) |
|---|
The exponential term of the above equation decays very fast. At solid electrodes, the contribution of the capacitive current is significant only at very high scan rates while at immiscible liquid-liquid interfaces it can be quite high. We derived above that the faradaic current is proportional to the square root of the scan rate. The total current iT is therefore
 |
(7.45) |
|---|
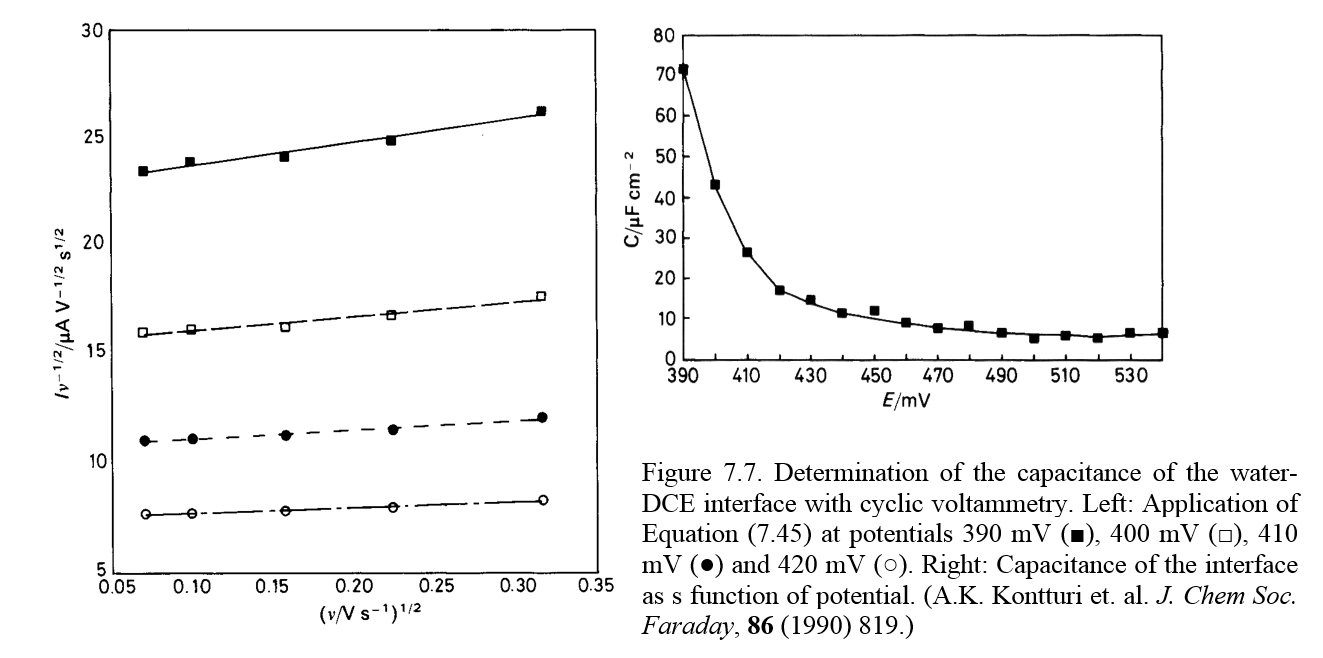
where A
is a constant. Plotting  as a function of
as a function of  at each potential, a
straight line is obtained with the slope of Cdl. Figure
7.7 shows just such an analysis of the water-1,2-dichloroethane (DCE) interface.
at each potential, a
straight line is obtained with the slope of Cdl. Figure
7.7 shows just such an analysis of the water-1,2-dichloroethane (DCE) interface.
7.1.3. Current step
When constant current is fed to an electrode, the boundary condition of the transport problem is known, making the solution easy. Since the Laplace transform of the constant current density i is i/s, the surface concentrations in the Laplace domain are (only ’R’ initially present)
 |
(7.46) |
|---|
 |
(7.47) |
|---|
After inverse transformation,
 |
(7.48) |
|---|
 |
(7.49) |
|---|
The moment
when the surface concentration of ’R’drops to zero is known as the transition time,  . It is given by the Sand equation:
. It is given by the Sand equation:
 |
(7.50) |
|---|
Surface concentrations can be written in a compact form with the transition time:
 |
(7.51) |
|---|
 |
(7.52) |
|---|
|
Calculation of the concentration profiles does not pose a problem either. The profile of ’R’in the Laplace domain is
A comparison of Figures 7.1 and 7.8 reveals the fundamental difference between potential and current steps: potential step fixes the surface concentration and current step the concentration gradient at the surface as a constant. |
|---|
The electrode potential is obtained as a function of time applying Equations (7.51) and (7.52):
![\displaystyle E=E^{0'}-\frac{RT}{nF}\text{ln} [ \xi(\sqrt{\frac{\tau}{t}}-1) ] \displaystyle E=E^{0'}-\frac{RT}{nF}\text{ln} [ \xi(\sqrt{\frac{\tau}{t}}-1) ]](https://mycourses.aalto.fi/filter/tex/pix.php/f1eb6f5c53f4f9b00e40d517e83aa938.gif) |
(7.55) |
|---|
Transition
time is therefore observed as the point at which the electrode potential changes
abruptly. Times t = 0 and  are,
in principle, singularities of Equation (7.55) but in practice this cannot
naturally happen. At these points, something else than the redox couple being investigated defines the electrode potential after transition time, most probably the
decomposition of the solvent.
are,
in principle, singularities of Equation (7.55) but in practice this cannot
naturally happen. At these points, something else than the redox couple being investigated defines the electrode potential after transition time, most probably the
decomposition of the solvent.
Experimental determination of the transition time is not, however, simple. Since the experiment is not carried out under potential control, the electrode potential may drift before the transition time to the hydrogen (on the cathode) or oxygen evolution region (on the anode). The reduction of metals in particular is only easy on the mercury electrode that has an exceptionally high overpotential of hydrogen evolution.
Figure 7.9. Electrode
potential as a function of time during a current step experiment; n = 1 and  =1.
=1.
Electrode capacitance adds yet another level of difficulty. Capacitive current iC is defined as
 |
(7.56) |
|---|
Equation (7.56) means that a certain portion of the current is consumed by charging the electric double layer. Since the double layer capacitance Cdl is also a function of the electrode potential, this makes an accurate quantitative analysis of the effect of the capacitance rather difficult.
* The meaning of s is discussed in greater detail in the chapter on the impedance technique; it represents frequency.
† Function y = exp(x2)erfc(x) can be approximated with high accuracy with the polynomial y = 0.34802 z - 0.09587 z2 + 0.74785 z3, where z = (1 + 0.47047 x)-1. From: M. Abramowitz ja I.A. Stegun (Ed.), Handbook of Mathematical Functions, 7. p., Dover, New York, 1970, p. 299.
[1] R.S. Nicholson, I. Shain, Anal. Chem. 36 (1964) 7066.
[2] |Es - Ep| = 112.5/n mV. From: R.S. Nicholson, Anal. Chem. 37 (1965) 1351.
‡ See, e.g. D. Britz, Digital Simulation in Electrochemistry, 2. Ed., Springer, Berlin, 1988.
[3] A.K. Kontturi et al. J Electroanal. Chem. 418 (l996) 131.








![\displaystyle\int_{0}^{\sigma t}{\sqrt{\sigma t-\tau}} (\frac{\partial\chi}{\partial \tau})d\tau=\sum\limits_{k=0}^{N-1}{\sqrt{\delta}} \int_{k}^{k+1}{\sqrt{N-k}} d\chi \approx {\sqrt{\delta}}\sum\limits_{k=0}^{N-1}{\sqrt{N-k}} [\chi(k+1)-\chi(k)] \displaystyle\int_{0}^{\sigma t}{\sqrt{\sigma t-\tau}} (\frac{\partial\chi}{\partial \tau})d\tau=\sum\limits_{k=0}^{N-1}{\sqrt{\delta}} \int_{k}^{k+1}{\sqrt{N-k}} d\chi \approx {\sqrt{\delta}}\sum\limits_{k=0}^{N-1}{\sqrt{N-k}} [\chi(k+1)-\chi(k)]](https://mycourses.aalto.fi/filter/tex/pix.php/5b2484d7b76c6300e86ba16655b63497.gif)


![\displaystyle\chi(N)=\chi(N-1)-\sum\limits_{k=0}^{N-1}{\sqrt{N-k}}[\chi(k+1)-\chi(k)]+\frac{1}{2\sqrt{\delta}}\frac{\theta_iS(N)C_r-1}{1+ \xi\theta_iS(N) } \displaystyle\chi(N)=\chi(N-1)-\sum\limits_{k=0}^{N-1}{\sqrt{N-k}}[\chi(k+1)-\chi(k)]+\frac{1}{2\sqrt{\delta}}\frac{\theta_iS(N)C_r-1}{1+ \xi\theta_iS(N) }](https://mycourses.aalto.fi/filter/tex/pix.php/5d09932ebccb2d077c10b3885ab482c7.gif)











![\displaystyle\bar c_{\text{R}}(x,t)=c_{\text{R}}^b -\frac{i}{nF\sqrt
D_{\text{R}}}\left(2\sqrt{\frac{t}{\pi}}\text{exp}\left(-{\frac{x^2}{4D_{\text{R}}t}}\right)-\frac{x}{\sqrt{D_{\text{R}}}}\text{erfc}\left(\frac{x}{2\sqrt{D_{\text{R}}t}}\right)\right)=c_{\text{R}}^b \left\lbrace{1-\sqrt{t}{\tau}} \left[\exp\left(-\frac{x^2}{4D_{\text{R}}t}\right)-\frac{\sqrt{\pi}x}{2\sqrt{D_{\text{R}}t}}\text{erfc}\left(\frac{x}{2\sqrt{D_{\text{R}}t}}\right)\right] \right\rbrace \displaystyle\bar c_{\text{R}}(x,t)=c_{\text{R}}^b -\frac{i}{nF\sqrt
D_{\text{R}}}\left(2\sqrt{\frac{t}{\pi}}\text{exp}\left(-{\frac{x^2}{4D_{\text{R}}t}}\right)-\frac{x}{\sqrt{D_{\text{R}}}}\text{erfc}\left(\frac{x}{2\sqrt{D_{\text{R}}t}}\right)\right)=c_{\text{R}}^b \left\lbrace{1-\sqrt{t}{\tau}} \left[\exp\left(-\frac{x^2}{4D_{\text{R}}t}\right)-\frac{\sqrt{\pi}x}{2\sqrt{D_{\text{R}}t}}\text{erfc}\left(\frac{x}{2\sqrt{D_{\text{R}}t}}\right)\right] \right\rbrace](https://mycourses.aalto.fi/filter/tex/pix.php/659d1f07739bd811ce5b8a7ef4e3751a.gif)