CHEM-A2600 - Kemiantekniikan ohjelmointikurssi, Luento-opetus, 22.4.2024-28.6.2024
This course space end date is set to 28.06.2024 Search Courses: CHEM-A2600
Python-oppimateriaali (CHEM-A2600)
scipy.stats
scipy.stats-moduuli sisältää valtavan määrän erilaisia tilastollisia funktioita ja jakaumafunktioita. Tämän kurssin puitteissa tutustumme vain scipy.stats.linregress-funktioon, jolla voi tehdä lineaarisen regressioanalyysin esimerkiksi mittausdatoille. Käytännössähän kyse on samasta suoran yhtälön sovituksesta, mitä olemme jo tehneet numpy.polyfit-funktion avulla 1. asteen polynomeille. linregress-funktio on kuitenkin suunniteltu juuri lineaariseen regressioon ja se myös palauttaa enemmän tietoja sovituksesta. Funktio palauttaa esimerkiksi korrelaatiokertoimen ja keskivirheen. Lisäksi linregress on laskennallisesti tehokkaampi hyvin suurille datajoukoille.
Tutustutaan linregress-funktioon esimerkin avulla. Meillä on käytössämme tiedosto T_p_data.txt, jossa on esitetty paine lämpötilan funktiona kaasumaiselle yhdisteelle (n = 0.65 mol). Mittausolosuhteet ovat sellaiset, että voimme odottaa ideaalikaasulain olevan voimassa.Tehtävänä on ratkaista astian tilavuus V.
- pV = nRT, joten p = nRT / V
- Kun paine esitetään lämpötilan funktiona ja mittausdatat sovitetaan suoran yhtälöön, sovitussuoran kulmakerroin on nR/V. Eli V = nR / kulmakerroin.
- Luetaan siis datat tiedostosta, tehdään niille lineaarinen regressio linregress-funktiolla ja ratkaistaan tilavuus V.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import linregress
from scipy.constants import R
n = 0.65 # mol
try:
# Luetaan datat tiedostosta
T_p_datat = np.loadtxt("T_p_data.txt")
except OSError:
print("Tiedoston T_p_data.txt avaaminen epaonnistui")
else:
# Lukeminen onnistui, luodaan kaksi yksiulotteista taulukkoa
T = T_p_datat[:, 0]
p = T_p_datat[:, 1]
# Lineaarinen regressio. T == x, p == y
slope, intercept, r_value, p_value, std_err = linregress(T, p)
# Sovitussuoran yhtälö: y = slope * x + intercept
# Lasketaan sovitussuoran arvot mitatuille x-arvoille (taulukko T)
p_sovitetut = slope * T + intercept
# Piirretään mittausdatat ja sovitussuora
plt.plot(T, p, '.', color = 'red', label = 'Mittaukset (T, p)')
# r_value on korrelaatiokerroin
teksti = "Sovitus (R$^2$ = {:.3f})".format(r_value**2)
plt.plot(T, p_sovitetut, '-', color = 'black', label = teksti)
# Kuvaajan akselit ja muut asetukset.
plt.xlim(300, 400)
plt.ylim(100000, 150000)
plt.xticks(np.arange(300, 401, 20))
plt.yticks(np.arange(100000, 150001, 10000))
plt.xlabel('T (K)')
plt.ylabel('p (Pa)')
plt.legend(loc = 'upper left')
# Ratkaistaan V == n * R / slope
# Tulostetaan V ja kulmakertoimen keskivirhe std_err
print("V: {:.3f} m^3".format(n * R / slope))
print("Kulmakertoimen keskivirhe: {:.1f}".format(std_err))
Koodi tulostaa
V: 0.015 m^3 Kulmakertoimen keskivirhe: 6.9
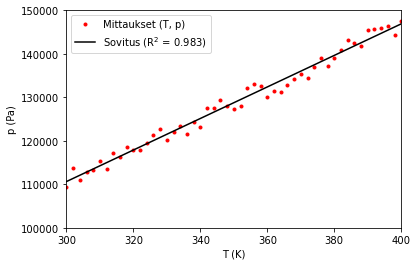
ja piirtää allaolevan kuvaajan
Tehtävä 6.3.1
