CHEM-E4106 - Electrochemistry D, Lecture, 10.1.2022-22.2.2022
This course space end date is set to 22.02.2022 Search Courses: CHEM-E4106
Kirja
3. Transport in electrolyte solutions
3.4. Analysis of transport equations in a steady state
The Nernst-Planck equation must be written out for each species in the solution. Constraints of the group of equations are the electroneutrality condition and electric current density:
 |
(2.3) |
|---|
 |
(3.14) |
|---|
The solution of the group is
possible in closed form,2 but let us highlight a couple of its important
features with the help of a binary electrolyte  . Division by diffusion
coefficients gives
. Division by diffusion
coefficients gives
 |
(3.38) |
|---|
Ionic concentrations are c+
=  +c and c- =
+c and c- =  -c, and the condition of electroneutrality can be written as z+
-c, and the condition of electroneutrality can be written as z+ + + z-
+ + z- - = 0. Summing above equations,
- = 0. Summing above equations,  is eliminated:
is eliminated:
 |
(3.39) |
|---|
With equation (3.14) and electroneutrality, the left had side of Equation (3.39) can be written as
 |
(3.40) |
|---|
and equation (3.38) using straightforward algebra:
 |
(3.41) |
|---|
The coefficient of the concentration gradient is the electrolyte diffusion coefficient D±:
 |
(3.42) |
|---|
Equation (3.42) is
known as the Nernst-Hartley equation. It is important to notice that, in
principle, only components, viz
electrolyte diffusion coefficients can be measured, although an electrochemical
measurement with a supporting electrolyte gives a very accurate approximation
of an ionic diffusion coefficient – this case known as a trace ion case is discussed
later. It is easy to use Equation (3.41) to check that z+J+
+ z-J- = i/F. The coefficient in front
of  is
is  where ti
is the transport number of the
ion. It is a measurable quantity (see paragraph 3.4.1) that tells us how large a fraction of electric current the ion carries in the solution. Adding up the convective terms of either Equation (3.33) or (3.41) gives
where ti
is the transport number of the
ion. It is a measurable quantity (see paragraph 3.4.1) that tells us how large a fraction of electric current the ion carries in the solution. Adding up the convective terms of either Equation (3.33) or (3.41) gives  , which tells us something elser important: electric current does not depend on convection. [1]
, which tells us something elser important: electric current does not depend on convection. [1]
The ratio of the electrolyte diffusion coefficient and the cation transport number gives:
 |
(3.43) |
|---|
that gives the desired connection between ionic diffusion coefficients and measurable quantities. Now we are able to write down the Nernst-Planck equation in a compact form of
 |
(3.44) |
|---|
Starting from the definition of the transport number, i.e. the fraction of carried current, the following alternative forms can be achieved using Equations (3.14) and (3.15):
 |
(3.45) |
|---|
You can check using a 2:1 electrolyte
 , or example, that Equations (3.44) and (3.41) give the
same result.
, or example, that Equations (3.44) and (3.41) give the
same result.
Combining Equations (3.38) and (3.44), a very important result is achieved: [2]
![\displaystyle\nabla\phi=-\frac{RT}{F} \left[
\frac{D_+-D_-}{z_+D_+-z_-D_-}\nabla\text{ln}c_++\frac{i/F}{z_+c_+(z_+D_+-z_-D_-)}\right]=-\frac{RT}{F}\left(\frac{t_+}{z_+}+\frac{t_-}{z_-}\right)\nabla\text{ln}c_+-\frac{i}{\kappa}
\displaystyle\nabla\phi=-\frac{RT}{F} \left[
\frac{D_+-D_-}{z_+D_+-z_-D_-}\nabla\text{ln}c_++\frac{i/F}{z_+c_+(z_+D_+-z_-D_-)}\right]=-\frac{RT}{F}\left(\frac{t_+}{z_+}+\frac{t_-}{z_-}\right)\nabla\text{ln}c_+-\frac{i}{\kappa}](https://mycourses.aalto.fi/filter/tex/pix.php/2882e4396a14140d3231cee101e8a86c.gif) |
(3.46) |
|---|
Equation (3.46) states
that the potential gradient in the solution is formed from two contributions,
diffusion potential and ohmic loss. Diffusion potential arises from the
differences in the ionic mobility. Although, say, a cation has a higher
mobility than an anion (see Equation (3.5)), they must move at the same velocity
in order to retain electroneutrality. This means that the anion is slowing down
the movement of the cation and, accordingly, the cation is speeding up the
movement of the anion. This is seen as diffusion potential. The magnitude of
diffusion potential is, however, rather small because the ionic mobilities are
usually of the same order of magnitude (H+ and OH- are exceptions due to their different
transport mechanism). Ohmic loss, in contrast, is always present in the
measurements; it is irreversible in nature because it leaves a system as a
heat loss (Joule heat). Check with a 2:1 electrolyte that Equation (3.46) truly
gives the term  .
.
It is easy to show that Equation (3.46) can be written in the general form of
 . . |
(3.47) |
|---|
In systems with more than two ions, the use of the above equation is hampered because transport numbers are no longer constants but instead depend on the local concentrations of ions. In electrochemical experiments, the problem is circumvented by adding an excess of a supporting electrolyte at least 50 times the amount of the electroactive ion that reacts on the electrode. This makes the transport number of the electroactive ion practically zero, it is transported solely by diffusion and the supporting electrolyte is primarily carried by current. An ion such as this is called a trace ion. On the electrode, however, the situation is completely reversed because the trace-ion carries all the current:
 |
(3.48) |
|---|
If the trace-ion is not converted to another trace-ion via the reaction, n = |zk|. In the following chapters we will see how an electrochemical measurement results in an ionic diffusion coefficient. Strictly speaking, it does not provide an entirely correct value because the concentration difference in the trace ion between the bulk and the surface – as small as it is – forces a similar difference in the counter-ion of the supporting electrolyte. However, since the supporting electrolyte moves mostly via migration (transport number » 0) it is able to react rapidly to the trace ion movement, i.e. to adjust its concentration profile and compensate for the trace ion charge. The compensation occurs instantaneously, causing only a tiny disturbance in the trace ion: the fluxes of the trace-ion and the supporting ion are said to be weakly coupled. A more thorough analysis of ionic coupling would require a deeper look at the theory of irreversible thermodynamics that is beyond the scope of this book.
3.4.1 Measurement of transport number
The measurement of
the transport number is one of the oldest electrochemical measurements. There
are basically three methods: the Hittorf method, the method of a moving boundary
and the electromotive force of a cell with transference. In the Hittorf method, cathode and anode compartments are connected via a thin capillary, with no
concentration gradient allowed to be formed during the experiment. When a charge of  is run through the cell, Q/(z+F)
mol of cations has been removed from the cathode compartment but the amount of cations that have arrived is only t+Q/(z+F)
mol. Their difference thus is
is run through the cell, Q/(z+F)
mol of cations has been removed from the cathode compartment but the amount of cations that have arrived is only t+Q/(z+F)
mol. Their difference thus is  . A similar analysis can be done for the anode
compartment. The transport number can be calculated by analyzing the composition of the cathode and anode compartments
after the experiment.
. A similar analysis can be done for the anode
compartment. The transport number can be calculated by analyzing the composition of the cathode and anode compartments
after the experiment.

The disadvantage of the Hittorf method is that the duration of an experiment cannot be very long in order to prevent a concentration gradient from forming in the capillary connecting the compartments. During a brief experiment only rather small changes in concentrations occur, meaning the chemical analysis may be inaccurate. Current cannot be increased to an unlimited extent either because it would dissipate in the cell as heat.
In the method of a moving boundary, a vertical
capillary is equipped with a cathode on the top and an anode on the bottom. Two solutions with a common ion (M+X– and
N+X–) are poured into the capillary, with the denser solution on
the bottom. In order to keep the boundary between the solutions sharp, the
mobility of M+ must be higher than that of N+. The
boundary resides initially at position A (see Figure 3.7). The system is
electrolyzed with the charge  , causing M+ to move upwards towards
the cathode. The amount of M+ transferred is (t+Q)/(z+F)
mol; the boundary is now at a new position B. The amount of M+
removed from the interval A-B is
, causing M+ to move upwards towards
the cathode. The amount of M+ transferred is (t+Q)/(z+F)
mol; the boundary is now at a new position B. The amount of M+
removed from the interval A-B is  (A is the area of the cross section of the capillary and
(A is the area of the cross section of the capillary and  the distance A-B). Equating these two expressions we find that
the distance A-B). Equating these two expressions we find that
 |
(3.49) |
|---|
The ingenuity of the method is that the boundary remains sharp and diffusion does not blur it. The lower and denser solution usually contains an indicator so the boundary can be observed with the naked eye.
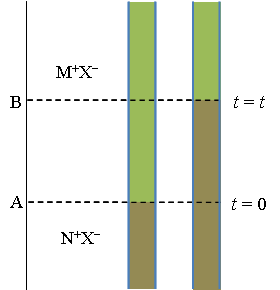
The velocity of an ion is given by Equation (3.5): vi = uiE. Since the conductivity of the lower solution, κ, is lower than in the upper solution the electric field E ~ i/κ is stronger in the lower solution. If M+ diffuses into the lower solution the stronger electric field accelerates it back into the upper solution, separating it from N+ that has lower mobility than M+. Accordingly, if N+ diffuses into the upper solution it experiences a lower electric field that decelerates it and it lags behind M+, bringing it back to the lower solution. However, if the conductivity of the lower solution is higher than in the upper solution the boundary does not remain sharp. A more detailed explanation is given in, I.N. Levine Physical Chemistry, McGraw-Hill, Tokio 1978, page 458-9 (removed from later editions!). |
|---|
Perhaps the most elegant method of determining a transport number is based on the electromotive force of a cell with transference, that is, its open circuit potential. For example, if two NaCl solutions at different concentrations are separated by a porous membrane or a frit that allows ions to diffuse across, Equation (3.46) gives the following for the diffusion potential (i = 0):
 |
(3.50) |
|---|
where
 and
and  refer
to the two compartments. If the electrodes are reversible to Cl–
anions, the Nernst equation contributes to the open circuit
potential, making the total potential
refer
to the two compartments. If the electrodes are reversible to Cl–
anions, the Nernst equation contributes to the open circuit
potential, making the total potential |
(3.51) |
|---|
where concentrations are replaced by activities (see Equation (3.36)). The sign must be chosen depending on which concentration
 is higher. The measurement must be carried
out with a voltage meter that has a very high input impedance to keep the
current zero. The concentration difference between the compartments cannot be very large either. Cell potentials are revisited in Chapter 4.
is higher. The measurement must be carried
out with a voltage meter that has a very high input impedance to keep the
current zero. The concentration difference between the compartments cannot be very large either. Cell potentials are revisited in Chapter 4.

