CHEM-E4106 - Electrochemistry D, Lecture, 10.1.2022-22.2.2022
This course space end date is set to 22.02.2022 Search Courses: CHEM-E4106
Kirja
2. Thermodynamics of electrolyte solutions
2.4. Solvent-ion interaction
Melting points of common salts are very high because the ions in the lattice are bound together with very strong electrostatic forces. They can dissolve, however, in polar solvents at rather high concentrations. The reason for this is the ability of the solvent molecules to solvate, i.e. to gather around ions, mainly using electrostatic forces. In the case of water, we talk about hydration and hydration number that is the number of water molecules bound by salt. For LiCl, the hydration number is 7, NaCl 3.5 and MgCl2 14. The hydration number is often assigned to the cation.
Free energies of hydration are negative and rather large, of the order of -300 to -4000 kJ/mol, which reflects the strength of the interactions between ions and water. The solubility of salts decreases with the relative permittivity, i.e. the polarity of the solvent, and in non-polar solvents common salts practically do not dissolve at all.
The interaction between a solvent and an ion is
traditionally estimated with the Born model that, despite being very simple, gives a
good picture of the electrostatics of solvation. In addition to the electrostatic
interaction, there are also other forces between ions and solvents that are
addressed in, for example, the scaled particle theory [1].
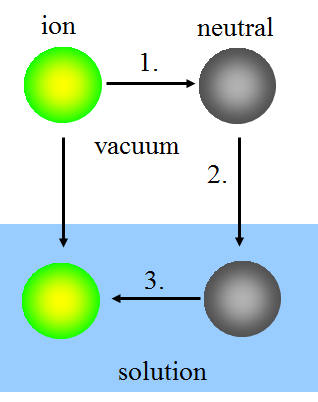
In the Born model, ion solvatation is thought to take place in three steps:
1. Uncharging the ion in vacuum.
2. Bringing the neutral species into the solution.
3. Charging the species in the solution.
The work to charge a species in vacuum is (a = ion radius)
 , , |
(2.25) |
|---|
Hence, the work Step 1 has an opposite sign to this. Charging a species in the solution has the work, accordingly
 |
(2.26) |
|---|
The electrostatic energy of ion solvation (IS) is therefore
 |
(2.27) |
|---|
The work (energy) of Step 2 > 0, because a cavity must be formed for a species in the solution. This work is ~(4/3)πa3P where P is pressure. When a species is brought through the solution surface, work must be done against the surface tension
 ; that work is
; that work is  .
.
The electrostatic energy is, however, so dominating and negative that solvation is a spontaneous process. Assume that a = 0.1 nm, z = 1 εr = 78.4, p = 1 atm ja γ = 0.0728 J/m2. The electrostatic energy is now -7.1 eV = -684 kJ/mol, while Step 2 has energy of only 0.057 eV = 5.5 kJ/mol. Although there are other forces in Step 2, we are no longer concerned with them.
If an ion is partitioned between an aqueous and an organic solution, Equation (2.27) can be applied via a thought process where an ion is brought from a vacuum into the both phases. The difference between the solvation energies becomes
 |
(2.28) |
|---|
From Equation (2.11) we see that
 The entropy of solvation
is therefore
The entropy of solvation
is therefore |
(2.29) |
|---|
 |
(2.30) |
|---|
For water (∂er/∂T) = -0.3595, giving the enthalpy share of
 -7.2 eV and
the entropy share
-7.2 eV and
the entropy share  = +0.1 eV at
room temperature. The entropy of solvation therefore increases as a result of issues that
are beyond electrostatics. Upon solvation, the solvent molecules are organized
around an ion in a configuration that is different from that in the bulk of the
solution, reducing the entropy of the solution. These issues are beyond the
scope of this book. An interested reader can look at the text book by Y.
Marcus [2].
= +0.1 eV at
room temperature. The entropy of solvation therefore increases as a result of issues that
are beyond electrostatics. Upon solvation, the solvent molecules are organized
around an ion in a configuration that is different from that in the bulk of the
solution, reducing the entropy of the solution. These issues are beyond the
scope of this book. An interested reader can look at the text book by Y.
Marcus [2].
Table 2.1. Standard Gibbs free energy, enthalpy and entropy of ion hydration and the molar volume in water for selected ions. From: Y. Marcus in, A.G. Volkov and D.W. Deamer (Eds.), Liquid/liquid interfaces. Theory and methods, CRC Press, Boca Raton, 1996. With the Publisher’s (CRC Press) permission.
|
|
|
|
|
|
|
|
|
|
|
Cations |
Radius/pm |
/kJ mol-1 |
/kJ mol-1 |
/J mol-1 K-1 |
/cm3 mol-1 |
|
|
|
H+ |
|
-1055 |
-1090 |
-131 |
-5.5 |
|
|
|
Li+ |
69 |
-475 |
-530 |
-161 |
-6.4 |
|
|
|
Na+ |
102 |
-365 |
-415 |
-130 |
-6.7 |
|
|
|
K+ |
138 |
-295 |
-330 |
-93 |
3.5 |
|
|
|
Rb+ |
149 |
-275 |
-305 |
-84 |
8.6 |
|
|
|
Cs+ |
170 |
-250 |
-280 |
-78 |
15.8 |
|
|
|
NH4+ |
148 |
-285 |
-325 |
-131 |
12.4 |
|
|
|
Me4N+ |
280 |
-160 |
-215 |
-163 |
84.1 |
|
|
|
Et4N+ |
337 |
-130 |
-205 |
-241 |
143.6 |
|
|
|
Mg2+ |
72 |
-1830 |
-1945 |
-350 |
-32.2 |
|
|
|
Ca2+ |
100 |
-1505 |
-1600 |
-271 |
-28.9 |
|
|
|
Fe2+ |
78 |
-1840 |
-1970 |
-381 |
-30.2 |
|
|
|
Ni2+ |
69 |
-1980 |
-2115 |
-370 |
-35 |
|
|
|
Fe3+ |
65 |
-4265 |
-4460 |
-576 |
-53 |
|
|
|
|
|
|
|
|
|
|
|
|
Anions |
|
|
|
|
|
|
|
|
F– |
133 |
-465 |
-510 |
-156 |
4.3 |
|
|
|
Cl– |
181 |
-340 |
-365 |
-94 |
23.3 |
|
|
|
Br– |
196 |
-315 |
-335 |
-78 |
30.2 |
|
|
|
I– |
220 |
-275 |
-290 |
-55 |
41.7 |
|
|
|
OH– |
133 |
-430 |
-520 |
-180 |
-0.2 |
|
|
|
NO3– |
179 |
-300 |
-310 |
-95 |
34.5 |
|
|
|
ClO4– |
250 |
-205 |
-245 |
-76 |
49.6 |
|
|
|
|
|
|
|
|
|
|
[1] A review of the theory is provided by R.A. Pierotti, Chem. Rev. 76 (1976) 717-726.
[2] Y. Marcus, Ion Solvation, Wiley, 1985.





