Kirja: Standard potential

4. Electrochemical cells

4.3. Standard potential

Quantity E⁰ in equations (4.5) and (4.17) is the standard value for cell potential. Thermodynamics defines certain standard conditions in order to enable reliable comparison of quantities and preparation of tables. In the example cell, the standard cell potential can be divided in two parts. These two parts are thought to be the contributions of the potential that each electrode reaction produces:


$E^0=E^0_{\text{Fe}^{3+}/\text{Fe}^{2+}}-E^0_{\text{H}^{+}/\text{H}_{2}}$	(4.18)

where


$-FE^0_{\text{H}^{+}/\text{H}_{2}}=\mu^0_{\text{H}^+}-\frac{1}{2}\mu^0_{\text{H}_2}$	corresponding to the half-cell Pt \| H⁺,H₂
$-FE^0_{\text{Fe}^{3+}/\text{Fe}^{2+}}=\mu^0_{\text{Fe}^{2+}}-\mu^0_{\text{Fe}^{3+}}$	corresponding to the half-cell Fe³⁺,Fe²⁺\| Au

Combining the half-cells gives the E⁰of the example cell:


$\displaystyle E^0=\frac{\mu^0_{\text{Fe}^{3+}}-\mu^0_{\text{Fe}^{2+}}-\mu^0_{\text{H}^{+}}+\mu^0_{\text{H}_{2}}}{F}=\frac{-\Delta G^0}{nF}$	(4.19)

The standard potential of the cell gives the work needed to transfer one electron between the gold electrode and the redox couple (Fe³⁺/Fe²⁺) in the solution, on a potential scale that is defined by the hydrogen electrode on the left side of the cell in standard conditions. Standard potentials of different half-cells are tabulated and combining these gives the standard cell potential of galvanic cells. The tabulated values of E⁰ also enable the estimation of spontaneity of different reactions. As seen from (4.19), the larger the value of standard reduction potential, the stronger the driving force for a particular reaction (as the more negative the value of Gibbs free energy change). This allows conclusions concerning half-reactions, e.g. choosing which half-reaction in galvanic cell is oxidation and which is reduction.

One has to keep in mind that the standard potential for a half-cell is not the same as the “absolute” electrode potential i.e. the galvani potential difference. The standard electrode potential for the half-cell Pt | H⁺,H₂ based on equation (4.13) is

$\displaystyle (\phi^{\sigma}-\phi^{\beta})=\frac{\frac{1}{2}\mu^0_{\text{H}_{2}}-\mu^0_{\text{H}^{+}}+\mu^{\beta}_{e^-}}{F}$

(4.20)

whereas $E^0_{\text{H}^+/\text{H}_2}$ is obtained from (4.17)

$\displaystyle E^0_{\text{H}^+/\text{H}_2}=\frac{\frac{1}{2}\mu^0_{\text{H}_{2}}-\mu^0_{\text{H}^{+}}}{F}$	(4.21)

$(\phi^{\sigma}-\phi^{\beta})$ and hence also

$E^0_{\text{H}^+/\text{H}_2}$ cannot either be measured. An auxiliary agreement is therefore needed to enable the potentials of the half-cells to be defined. According to the standard hydrogen electrode convention of IUPAC[1], the half-cell potential of the standard hydrogen electrode (left side of Figure 4.2.) at all temperatures is zero:


$E^0_{\text{H}^{+}/\text{H}_{2}} \equiv0\text{V}$	(4.22)

Example 1: Why is FeCl₃used to dissolve copper in the manufacture of circuit boards? Justify your answer with the standard reduction potentials below.

$E^0_{{\text{Fe}^{3+}}/{\text{Fe}^{2+}}}=0.77\text{V}$ $E^0_{{\text{Cu}^{2+}}/{\text{Cu}^{+}}}=0.34\text{V}$

Tabulated values of reduction potentials correspond to the standard potentials of the following reactions:

Fe³⁺ + e^– → Fe²⁺ E⁰= 0.77 V

Cu²⁺ + 2e^– → Cu E⁰= 0.34 V

Let us combine these into a reaction where Fe(III) ions dissolve metallic copper:

2Fe³⁺ + 2e^– → 2Fe²⁺ E⁰= 0.77 V

Cu → Cu²⁺ + 2e^– E⁰ = –0.34 V

____________________________________________________________________________

2Fe³⁺ + Cu →2Fe²⁺ + Cu²⁺E⁰_total= 0.43 V

When combining half-reactions, one has to remember to balance the number of transferring electrons by multiplying the half-reactions with appropriate numbers. Even if the half-reaction is multiplied by a number (like here the reaction of iron by 2), the corresponding standard potential is not multiplied as the potential is an intensive quantity. Both DG⁰ and n are extensive quantities, so the ratio of them is an intensive quantity (not dependent on the amount of substance). The tabulated potential values are for reduction, and since the reaction of copper is reversed for oxidation, the sign of the corresponding potential is also reversed. The standard cell potential for the total cell reaction is obtained as the sum of the half-reaction potentials (potential is a state function). The Gibbs free energy change for the reaction (in standard conditions) is obtained as:

$\Delta G^0=-nFE^0=-2\text{mol} \times96485\frac{\text{C}}{\text{mol}} \times0.43\frac{\text{J}}{\text{C}} =-83\text{kJ}$

The reaction is spontaneous as the Gibbs free energy change is negative. A Fe(III) ion in the solution will dissolve (oxidize) metallic copper.

4.3.1 Standard potential values

The standard potential E⁰ of a cell can be obtained in four ways:

· from the standard Gibbs free energy change of the virtual total cell reaction

· from the tabulated standard reduction potentials of the half-reactions

· from the equilibrium constant K of the virtual total cell reaction

· extrapolating from experimental results


Example 2: There are two approaches in the literature to calculate the E⁰ of a (galvanic) cell from the tabulated values of the E⁰ of half-reactions. Example 1 presents the approach where one of the two reduction reactions is reversed into an oxidation reaction. As the half-reaction is reversed, the sign of the reduction potential is changed. A virtual net cell reaction is obtained by adding the reduction and oxidation reactions, and because the potential is a state function, the potential of the sum reaction (the net cell reaction) is obtained as the sum of the reduction and oxidation potentials. E.g. Daniel cell: Zn \| 1.0 M Zn²⁺ \|\| 1.0 M Cu²⁺\| Cu Reduction potentials from a table: Zn²⁺+ 2e^– $\ce{ -> }$ Zn E⁰ = –0.76 V Cu²⁺+ 2e^– $\ce{ -> }$ Cu E⁰ = 0.34 V The reaction of zinc is reversed to an oxidation reaction and the sign of the corresponding potential is changed. The virtual net cell reaction and its standard potential E⁰ is obtained as a sum: Zn $\ce{ -> }$ Zn²⁺+ 2e^– E⁰ = 0.76 V Cu²⁺+ 2e^– $\ce{ -> }$ Cu E⁰ = 0.34 V _____________________________________________________________ Zn + Cu²⁺ $\ce{ -> }$ Zn²⁺+ Cu E⁰ = 0.76 V+ 0.34 V = 1.1 V According to the second approach, the cell potential is calculated from equation (4.4) as E_cell= E_right– E_left. In a galvanic cell, the reaction on the right is reduction and the reaction on the left is oxidation. Therefore, for the Daniel cell: E⁰ = 0.34V – (–0.76 V) = 1.1 V It is necessary to know which of the half-reactions is reduction and which is oxidation. The rule of thumb is that the reaction that has the lower reduction potential is converted to oxidation.

Quite often one needs to measure the standard potential of a half-reaction. As the standard hydrogen electrode defines the zero of the potential scale, the desired half-cell can be determined by constructing a cell that has this as the other electrode. A silver-silver chloride electrode is a typical reference electrode, which can be prepared by electrolyzing a silver wire in a solution containing chloride, thus forming a solid layer of silver chloride at the surface of the silver wire. In order to find the standard potential of the silver-silver chloride electrode, the following cell can be constructed in standard conditions:


Cu \| Pt \| H_2,HCl \| AgCl \| Ag \| Cu’	(4.23)

Half-reactions are now written in terms of reduction, like the tabulated values:


Ag⁺ + e^– $\ce{ }$ Ag	(4.24a)
H⁺ + e^– $\ce{ }$ ½ H₂	(4.24b)

The cell potential is obtained from the corresponding Nernst equations and equation (4.4):


$\displaystyle E=\left[E^0_{\text{Ag}^+/\text{Ag}}+\frac{RT}{F}\ln\left(\frac{a_{\text{Ag}^+}}{a_{\text{Ag}}}\right)\right]-\left[E^0_{\text{H}^+/\text{H}_2}+\frac{RT}{F}\ln\left(\frac{a_{\text{H}^+}}{(a_{\text{H}_2})^{1/2}}\right)\right]$	(4.25)

Let us assume that the silver electrode is made of pure silver and, therefore, its activity is one. In addition, equation (4.22) defines that the standard reduction potential of H⁺/H₂ is zero, and equation (4.25) becomes


$\displaystyle E=E^0_{\text{Ag}^+/\text{Ag}}+\frac{RT}{F}\ln\left(\frac{a_{\text{Ag}^+}(a_{\text{H}_2})^{1/2}}{a_{\text{H}^+}}\right)$	(4.26)

At the surface of the right-hand side electrode of cell (4.23), the equilibrium is achieved with chloride ions. Silver chloride is a sparingly soluble salt, and the chloride ion activity can be taken into equation (4.26) with the help of the solubility product, K_s = 1.77×10^–10. It is the equilibrium constant of the reaction:


AgCl $\ce{ }$ Ag⁺+ Cl^–	(4.27)

Hence, because AgCl is a pure, solid compound with the unit activity,


$\displaystyle K_s=\frac{a_{\text{Ag}^+}a_{\text{Cl}^-}}{a_{\text{AgCl}}}=a_{\text{Ag}^+}a_{\text{Cl}^-}\cong\frac{c_{\text{Ag}^+}c_{\text{Cl}^-}}{(c^0)^2}$	(4.28)

Combining (4.26) and (4.28), and replacing the activity of the gas with its fugacity ratio at the reference pressure (according to the definition of activity) gives:


$\displaystyle E= E^0_{\text{Ag}^+/\text{Ag}}+\frac{RT}{F}\ln\left(\frac{K_s(a_{\text{H}_2})^{1/2}}{a_{\text{H}^+}a_{\text{Cl}^-}}\right)= E^0_{\text{Ag}^+/\text{Ag}}+\frac{RT}{F}\ln K_s+\frac{RT}{2F}\ln\left(\frac{f_{\text{H}_2}}{p^0}\right)-\frac{RT}{F}\ln(a_{\text{H}^+}a_{\text{Cl}^-})$	(4.29)

Constant terms in (4.29) form the standard reduction potential of the Ag/AgCl electrode. The value of this standard potential can be calculated from the standard reduction potential of silver and the solubility product of AgCl:


$\displaystyle E^0_{\text{AgCl/Ag}}=E^0_{\text{Ag}^+/\text{Ag}}+\frac{RT}{F}\ln K_s=0.799\text{ V}-0.577\text{ V}=0.222\text{ V}$	(4.30)

If the fugacity of the hydrogen gas is kept constant at 1 bar (standard conditions), the third term on the right-hand side of equation (4.29) is zero. In this case, the cell potential of (4.22) is a direct function of HCl concentration. Measuring the cell potential as a function of the concentration and extrapolating to infinite dilution, where the activity coefficient can be estimated with unity, the experimental value for standard reduction potential is obtained:


$\displaystyle E^0_{\text{AgCl/Ag}}=\lim\left(E+\frac{RT}{F}\ln(c_{\text{H}^+}c_{\text{Cl}^-})\right)_{c_{\text{HCl}}\rightarrow0}$	(4.31)

A hydrogen electrode with bubbled gas supply is not the most practical choice. As a matter of fact, the Ag/AgCl electrode in the previous example is currently the most popular reference electrode. Another popular choice is the calomel electrode, although it contains mercury salts (e.g. Hg₂Cl₂). Figure 4.3. presents the measurement of cell potential with Ag/AgCl electrode as the reference electrode instead of the hydrogen electrode.

A galvanic cell for the determination of the standard potentials using the Ag/AgCl reference electrode.

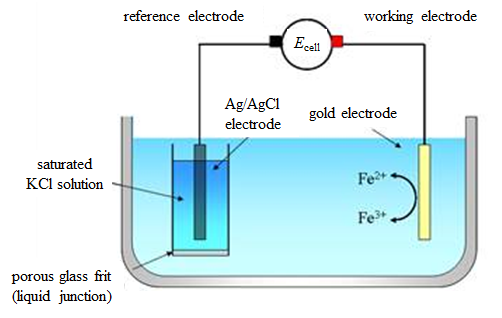
Figure 4.3. A galvanic cell for the determination of the standard potentials using the Ag/AgCl reference electrode.

This cell can be represented by the following cell diagram:


Cu \| Ag \| AgCl \| KCl(sat.) \|\| Fe³⁺, Fe²⁺\| Au \|Cu’	(4.32)

The cell potential is


$\displaystyle E=\left[E^0_{\text{Fe}^{3+}/\text{Fe}^{2+}}+\frac{RT}{F}\ln\left(\frac{a_{\text{Fe}^{3+}}}{a_{\text{Fe}^{2+}}}\right)\right]-\left[E^0_{\text{AgCl/Ag}}-\frac{RT}{F}\ln(a_{\text{Cl}^-})\right]$	(4.33)

Combining the constant terms in equation (4.33) (activity of Cl⁻ is constant because the solution is saturated) gives


$\displaystyle E=\left[E^{\text{0,AgCl/Ag}}_{\text{Fe}^{3+}/\text{Fe}^{2+}}+\frac{RT}{F}\ln\left(\frac{a_{\text{Fe}^{3+}}}{a_{\text{Fe}^{2+}}}\right)\right]$	(4.34)

where $E^{\text{0,AgCl/Ag}}_{\text{Fe}^{3+}/\text{Fe}^{2+}}$ is the standard reduction potential for the Fe(II)/Fe(III) redox pair on the scale of the Ag/AgCl reference electrode with the saturated KCl solution. As with the measurement with the standard hydrogen electrode, cell potentials are measured at different iron ion concentrations and the results extrapolated to infinite dilution to access the standard potential at the working electrode.

Standard potentials can also be determined with other experimental methods. Chapter 7 describes the use of cyclic voltammetry to determine the standard potential of a half-reaction. In addition, standard potentials can be resolved by combining electrochemical methods with spectroscopic methods.

4.3.2 Standard potentials on absolute scale

Electrochemical methods are used to measure the ionization potentials of conducting polymers or to determine the HOMO and LUMO orbital energies of organic molecules. The values typically obtained with cyclic voltammetry and the Ag/AgCl reference electrode need to be converted into what is known as the absolute scale and presented in electron volts (eV). The reference point of the absolute scale is a vacuum and the scale is also called the ‘vacuum scale’. The link between the standard hydrogen scale and the absolute scale is derived next. A more detailed account can be found in the literature[2].

Let us consider a case in which the standard potential of a redox couple in a solution is measured with the standard hydrogen electrode as the reference electrode. Let us assume that the electrostatic effect due to the surface potential of the electrolyte can be omitted (c ^s=0).


$\displaystyle E^{0, \text{abs}}_{\text{red/ox}}=\phi^{\text{metal}}-\phi^{\text{solution}}-\frac{\mu^{\text{M}}_{\text{e}}}{F}+\chi^S=\frac{\left(\alpha^0_{\text{H}^+}-\frac{1}{2}\mu^0_{\text{H}_2}\right)}{F}$	(4.35)

$E^{0, \text{abs}}_{\text{red/ox}}$ is the standard reduction potential of the redox couple on the absolute scale, $\alpha^0_{\text{H}^+}$ is the true standard chemical potential of the proton in the solution (i.e. the electrochemical potential in a non-charged environment) and $\mu^0_{\text{H}_2}$ is the standard chemical potential of the gaseous hydrogen molecule. In order to find the value of equation (4.35), it is very important to use the same reference point for all the quantities in the equation, the reference point being a vacuum. The standard chemical potential for a gaseous hydrogen molecule can be estimated from the ionization energy of the hydrogen atom and the covalent bond energy of the hydrogen molecule:

H⁺(g) + e⁻(g) $\ce{ }$ H(g) $\Delta$ G⁰= −13.613 eV

H(g) $\ce{ }$ ½ H₂(g) $\Delta$ G⁰= −2.107 eV

The real standard chemical potential of the proton in an aqueous solution is

H⁺(g) $\ce{ }$ H⁺(aq) $\alpha^0_{\text{H}^+}$ −11.276 eV

The standard potential of the hydrogen electrode on the absolute scale in Volts is:


$\displaystyle E^{0,\text{abs}}_{\text{H}^+/\text{H}_2}\cong\left[-11.276-(-13.613-2.107)\right]=4.44\text{ V}$	(4.36)

The potential values measured with reference to the standard hydrogen electrode (SHE) can be converted to the absolute scale with


$E^{0, \text{abs}}_{\text{Red/Ox}}\cong E^{0, \text{SHE}}_{\text{Red/Ox}}+4.44\text{ V}$	(4.37)

If the potential values have been determined using another reference electrode, the potential values are first converted to the SHE scale and then to the absolute scale. Potential values for different reference electrodes can be found in the literature (taking into account the different concentrations of the inner solutions of the electrodes) at different temperatures.


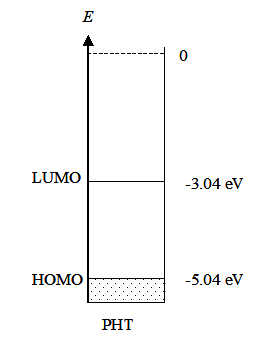
Example 3: Energy diagram to be drawn for the conducting polymer polyhexylthiphene (PHT) based on the following information: the oxidation potential from cyclic voltammetry for the polymer E’_ox (vs. Ag/AgCl) was 0.40 V and the band gap E_g from spectroscopic measurements was 2.0 eV. Solution: An energy diagram presents the HOMO (highest occupied molecular orbital) and the LUMO (lowest un-occupied molecular orbital) of a molecule. In solid substances, these are called the valence band and the conduction band, respectively. These can be estimated from the first oxidation potential of a semiconductor (HOMO, valence band) and the first reduction potential (LUMO, conduction band). The ionization energy (IE) of PHT, i.e. the energy of HOMO is obtained from the oxidation potential that is measured with cyclic voltammetry. The measurement used Ag/AgCl as the reference electrode so the value of the potential has to be converted to the absolute scale. The standard potential of Ag/AgCl electrode (25 °C, saturated KCl solution) is +0.199 V on the standard hydrogen scale, and the oxidation potential on the SHE scale is: E’_ox(vs. SHE) = E’_ox(vs. Ag/AgCl) + 0.199V = 0.40 V + 0.199 V = 0.60 V, and converted further to the absolute scale according to equation (4.37): E_ox(abs) = 0.60 V + 4.44 V = 5.04 V, and to electron volts IE =e E_ox(abs) = 5.04 eV The energy diagram can now be drawn:

[1] IUPAC = International Union of Pure and Applied Chemistry

[2] H.H. Girault, Analytical and Physical Electrochemistry, EPFL Press, 2004.

CHEM-E4106 - Electrochemistry D, Lecture, 10.1.2022-22.2.2022

Kirja

4. Electrochemical cells

4.3. Standard potential

4.3.1 Standard potential values

4.3.2 Standard potentials on absolute scale

Students

Teachers

About service