CHEM-E4106 - Electrochemistry D, Lecture, 10.1.2022-22.2.2022
This course space end date is set to 22.02.2022 Search Courses: CHEM-E4106
Kirja
7. Electrochemical methods
7.3. Ultramicroelectrodes
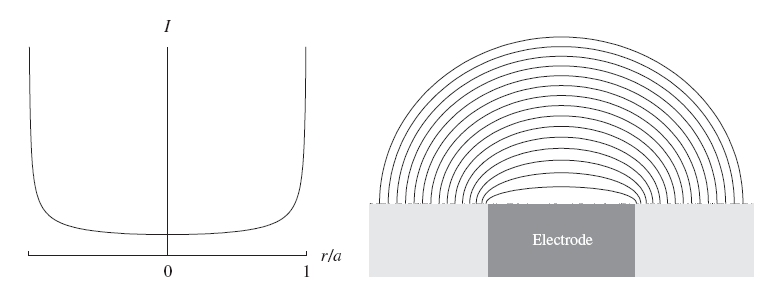
Figure 7.16. Radial current distribution (left) and equi-concentration lines (right) on a disk electrode.
As can be seen in Figure 7.16, the local current density increases very significantly towards the electrode edges. It can be shown that the radial distribution under mass transfer control is of the form
 |
(7.74) |
|---|
where a is the disk radius. The current density is therefore in principle, unlimited at the edge r = a, but the integral over the disk remains limited. In reality, current density is kinetically limited at the edge of the disk. When the disk radius a is reduced down to a few microns, the concentration profile becomes nearly spherically symmetrical (see the right-hand panel of Figure 7.16), and Equation (7.57) can be used.
Ultramicroelectrodes
are used in both transient and steady-state methods. In a steady-state, Equation
(7.58) gives with the boundary conditions c( ) = cb
and c(r = a) = 0 the concentration profile
) = cb
and c(r = a) = 0 the concentration profile
 |
(7.75) |
|---|
and the limiting current density
 |
(7.76) |
|---|
If the electrode really were a hemisphere, the limiting current would be
 , but Fleischmann and Pons have shown [1] that the limiting current of a disk ultramicroelectrode
is
, but Fleischmann and Pons have shown [1] that the limiting current of a disk ultramicroelectrode
is
 |
(7.77) |
|---|
In practice, calculations are made in spherical geometry and the results are corrected as above.
In transient methods, the general Equation (7.4) takes the form
 |
(7.78) |
|---|
proving that
when  the problem returns to linear geometry. Setting
the surface concentration to zero, current density in a potential step
experiment is in the Laplace domain
the problem returns to linear geometry. Setting
the surface concentration to zero, current density in a potential step
experiment is in the Laplace domain
 |
(7.79) |
|---|
After inverse transformation the result is
 |
(7.80) |
|---|
Comparing this result with the Cottrell equation (7.11) of linear geometry, it is seen that the current density levels out after the transient period to Equation (7.76), contrary to the Cottrell equation in which the current decays to zero.
Figure 7.17. Current transients (7.76). For the
Cottrell equation (7.11),  .
.
Figure
7.18. Cyclic voltammograms of an ultramicroelectrode at varying scan rates: v = 0.01 (blue), 0.1 (green) and 1.0 (red)
Vs-1; electrode radius a = 10  m.
m.
[1] M. Fleischmann, S. Pons, in: D.R. Rolison, P.P. Schmidt (Eds.), Ultramicroelectrodes, Datatech Systems, Morganton, N.C., 1987.
