MS-A0111 - Differential and Integral Calculus 1, Lecture, 5.9.2022-19.10.2022
This course space end date is set to 19.10.2022 Search Courses: MS-A0111
Differential and Integral Calculus
1. Sequences
Basics of sequences
This section contains the most important definitions about sequences. Through these definitions the general notion of sequences will be explained, but then restricted to real number sequences.
Note. Characteristics of the set  give certain characteristics to the sequence. Because
give certain characteristics to the sequence. Because  is ordered, the terms of the sequence are ordered.
is ordered, the terms of the sequence are ordered.
Definition: Terms and Indices
A sequence can be denoted denoted as
instead of  The numbers
The numbers  are called the terms of the sequence.
are called the terms of the sequence.
Because of the mapping
 we can assign a unique number
we can assign a unique number  to each term. We write this number as a subscript and define it as the index; it follows that we can identify any term of the sequence by its index.
to each term. We write this number as a subscript and define it as the index; it follows that we can identify any term of the sequence by its index.
A few easy examples
Example 1: The sequence of natural numbers
The sequence  defined by
defined by  is called the sequence of natural numbers. Its first few terms are:
is called the sequence of natural numbers. Its first few terms are:
 This special sequence has the property that every term is the same as its index.
This special sequence has the property that every term is the same as its index.
![]()
Example 2: The sequence of triangular numbers
Triangular numbers get their name due to the following geometric visualization: Stacking coins to form a triangular shape gives the following diagram:
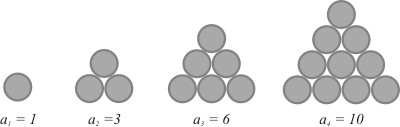
To the first coin in the first layer we add two coins in a second layer to form the second picture  . In turn, adding three coins to
. In turn, adding three coins to  forms
forms  . From a mathematical point of view, this sequence is the result of summing natural numbers. To calculate the 10th triangular number we need to add the first 10 natural numbers:
. From a mathematical point of view, this sequence is the result of summing natural numbers. To calculate the 10th triangular number we need to add the first 10 natural numbers:
 In general form the sequence is defined as:
In general form the sequence is defined as: 

This motivates the following definition:
Example 3: Sequence of square numbers
The sequence of square numbers  is defined by:
is defined by:  . The terms of this sequence can also be illustrated by the addition of coins.
. The terms of this sequence can also be illustrated by the addition of coins.
Interestingly, the sum of two consecutive triangular numbers is a square number. So, for example, we have:  and
and  . In general this gives the relationship:
. In general this gives the relationship:

Example 4: Sequence of cube numbers
Analogously to the sequence of square number, we give the definition of cube numbers as  The first terms of the sequence are:
The first terms of the sequence are:  .
.
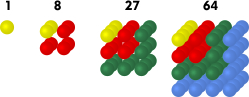
Example 5.
Example 6.
Given the sequence  with
with  , i.e.
, i.e.
 Let
Let  be its 1st difference sequence. Then it follows that
be its 1st difference sequence. Then it follows that
 A term of
A term of  has the general form
has the general form

Some important sequences
There are a number of sequences that can be regarded as the basis of many ideas in mathematics, but also can be used in other areas (e.g. physics, biology, or financial calculations) to model real situations. We will consider three of these sequences: the arithmetic sequence, the geometric sequence, and Fibonacci sequence, i.e. the sequence of Fibonacci numbers.
The arithmetic sequence
There are many definitions of the arithmetic sequence:
Definition A: Arithmetic sequence
A sequence  is called the arithmetic sequence, when the difference
is called the arithmetic sequence, when the difference  between two consecutive terms is constant, thus:
between two consecutive terms is constant, thus:

Note: The explicit rule of formation follows directly from definition A:
 For the
For the  th term of an arithmetic sequence we also have the recursive formation rule:
th term of an arithmetic sequence we also have the recursive formation rule:

Definition B: Arithmetic sequence
A non-constant sequence  is called an arithmetic sequence (1st order) when its 1st difference sequence is a sequence of constant value.
is called an arithmetic sequence (1st order) when its 1st difference sequence is a sequence of constant value.
This rule of formation gives the arithmetic sequence its name: The middle term of any three consecutive terms is the arithmetic mean of the other two, for example:
Example 1.
The sequence of natural numbers
 is an arithmetic sequence, because the difference,
is an arithmetic sequence, because the difference,  , between two consecutive terms is always given as
, between two consecutive terms is always given as  .
.
The geometric sequence
The geometric sequence has multiple definitions:
Definition: Geometric sequence
A sequence  is called a geometric sequence when the ratio of any two consecutive terms is always constant
is called a geometric sequence when the ratio of any two consecutive terms is always constant  , thus
, thus

Note.The recursive relationship
 of the terms of the geometric sequence and the explicit formula for the calculation of the n
th term of a geometric sequence
of the terms of the geometric sequence and the explicit formula for the calculation of the n
th term of a geometric sequence
 follows directly from the definition.
follows directly from the definition.
Again the name and the rule of formation of this sequence are connected: Here, the middle term of three consecutive terms is the geometric mean of the other two, e.g.:

Example 2.
Let  and
and  be fixed positive numbers. The sequence
be fixed positive numbers. The sequence  with
with  , i.e.
, i.e.
 is a geometric sequence. If
is a geometric sequence. If  the sequence is monotonically increasing. If
the sequence is monotonically increasing. If  it is strictly decreasing. The corresponding range
it is strictly decreasing. The corresponding range  is finite in the case
is finite in the case  (namely, a singleton), otherwise it is infinite.
(namely, a singleton), otherwise it is infinite.
The Fibonacci sequence
The Fibonacci sequence is famous because it plays a role in many biological processes, for instance in plant growth, and is frequently found in nature. The recursive definition is:
Definition: Fibonacci sequence
Let  and let
and let
 for
for  . The sequence
. The sequence  is then called the Fibonacci sequence. The terms of the sequence are called the Fibonacci numbers.
is then called the Fibonacci sequence. The terms of the sequence are called the Fibonacci numbers.
The sequence is named after the Italian mathematician Leonardo of Pisa (ca. 1200 AD), also known as Fibonacci (son of Bonacci). He considered the size of a rabbit population and discovered the number sequence:

Example 3.
The structure of sunflower heads can be described by a system of two spirals, which radiate out symmetrically but contra rotating from the centre; there are 55 spirals which run clockwise and 34 which run counter-clockwise.
Pineapples behave very similarly. There we have 21 spirals running in one direction and 34 running in the other. Cauliflower, cacti, and fir cones are also constructed in this manner.

Convergence, divergence and limits
The following chapter deals with the convergence of sequences. We will first introduce the idea of zero sequences. After that we will define the concept of general convergence.
Preliminary remark: Absolute value in 
The absolute value function  is fundamental in the study of convergence of real number sequences. Therefore we should summarise again some of the main characteristics of the absolute value function:
is fundamental in the study of convergence of real number sequences. Therefore we should summarise again some of the main characteristics of the absolute value function:
Graph of the absolute value function
Theorem: Calculation Rule for the Absolute Value
Parts 1.-3. Results follow directly from the definition and by dividing it up into separate cases of the different signs of  and
and 
Part 4. Here we divide the triangle inequality into different cases.
Case 1.
First let  . Then it follows that
. Then it follows that
 and the desired inequality is shown.
and the desired inequality is shown.
Finally we consider the case  and
and  . Here we have two subcases:
. Here we have two subcases:
For
 we have
we have  and thus
and thus  from the definition of absolute value. Because
from the definition of absolute value. Because  then
then  and therefore also
and therefore also  . Overall we have:
. Overall we have:

For
 then
then  . We have
. We have  . Because
. Because  , we have
, we have  and thus
and thus  . Overall we have:
. Overall we have:

The case  and
and  we prove it analogously to the case 3, in which
we prove it analogously to the case 3, in which  and
and  are exchanged.
are exchanged.
Zero sequences
Definition: Zero sequence
A sequence  s called a zero sequence, if for every
s called a zero sequence, if for every  there exists an index
there exists an index  such that
such that
 for every
for every  . In this case we also say that the sequence converges to zero.
. In this case we also say that the sequence converges to zero.
Informally: We have a zero sequence, if the terms of the sequence with high enough indices are arbitrarily close to zero.
Example 1.
The sequence  defined by
defined by  , i.e.
, i.e.  is called the harmonic sequence. Clearly, it is positive for all
is called the harmonic sequence. Clearly, it is positive for all  , however as
, however as  increases the absolute value of each term decreases getting closer and closer to zero.
increases the absolute value of each term decreases getting closer and closer to zero.
Take for example  , then choosing the index
, then choosing the index  , it follows that
, it follows that  , for all
, for all  .
.
The harmonic sequence converges to zero
Example 2.
Consider the sequence
 Let
Let  .We then obtain the index
.We then obtain the index  in this manner that for all terms
in this manner that for all terms  where
where 
 .
.
Note. To check whether a sequence is a zero sequence, you must choose an (arbitrary)  where
where  . Then search for a index
. Then search for a index  , after which all terms
, after which all terms  are smaller then said
are smaller then said  .
.
Example 3.
We consider the sequence  , defined by
, defined by

Because of the factors  two consecutive terms have different signs; we call a sequence whose signs change in this way an alternating sequence.
two consecutive terms have different signs; we call a sequence whose signs change in this way an alternating sequence.
We want to show that this sequence is a zero sequence. According to the definition we have to show that for every  there exist
there exist  , such that we have the inequality:
, such that we have the inequality:
 for every term
for every term  where
where  .
.
Theorem: Characteristics of Zero sequences
Parts 1 and 2. If  is a zero sequence, then according to the definition there is an index
is a zero sequence, then according to the definition there is an index  , such that
, such that  for every
for every  and an arbitrary
and an arbitrary  . But then we have
. But then we have  ; this proves parts 1 and 2 are correct.
; this proves parts 1 and 2 are correct.
Part 3. If  , then the result is trivial. Let
, then the result is trivial. Let  and choose
and choose  such that
such that
 for all
for all  .
Rearranging we get:
.
Rearranging we get:

Part 4.
Because  is a zero sequence, by the definition we have
is a zero sequence, by the definition we have  for all
for all  . Analogously, for the zero sequence
. Analogously, for the zero sequence  there is a
there is a  with
with  for all
for all  .
.
Then for all  it follows (using the triangle inequality) that:
it follows (using the triangle inequality) that:

Convergence, divergence
The concept of zero sequences can be expanded to give us the convergence of general sequences:
Example 4.
We consider the sequence  where
where
 By plugging in large values of
By plugging in large values of  , we can see that for
, we can see that for 
 and therefore we can postulate that the limit is
and therefore we can postulate that the limit is  .
.
For a vigorous proof, we show that for every  there exists an index
there exists an index  , such that for every term
, such that for every term  with
with  the following relationship holds:
the following relationship holds:

Firstly we estimate the inequality:

Now, let  be an arbitrary constant. We then choose the index
be an arbitrary constant. We then choose the index  , such that
, such that
 Finally from the above inequality we have:
Finally from the above inequality we have:
 Thus we have proven the claim and so by definition
Thus we have proven the claim and so by definition  is the limit of the sequence.
is the limit of the sequence.
If a sequence is convergent, then there is exactly one number which is the limit. This characteristic is called the uniqueness of convergence.
Assume  ; choose
; choose  with
with  Then in particular
Then in particular ![[a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset. [a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset.](https://mycourses.aalto.fi/filter/tex/pix.php/4bac60723e473d9697be98685ce7659a.gif)
Because  converges to
converges to  , there is, according to the definition of convergence, a index
, there is, according to the definition of convergence, a index  with
with  for
for  Furthermore, because
Furthermore, because  converges to
converges to  there is also a
there is also a  with
with  for
for  For
For  we have:
we have:
 Consequently we have obtained
Consequently we have obtained  , which is a contradiction as
, which is a contradiction as  . Therefore the assumption must be wrong, so
. Therefore the assumption must be wrong, so  .
.
Definition: Divergent, Limit
If provided that a sequence  and an
and an  exist, to which the sequence converges, then the sequence is called convergent and
exist, to which the sequence converges, then the sequence is called convergent and  is called the limit of the sequence, otherwise it is called divergent.
is called the limit of the sequence, otherwise it is called divergent.
Notation.  is convergent to
is convergent to  is also written:
is also written:
 Such notation is allowed, as the limit of a sequence is always unique by the above Theorem (provided it exists).
Such notation is allowed, as the limit of a sequence is always unique by the above Theorem (provided it exists).
Rules for convergent sequences
Theorem: Rules
Let  and
and  be sequences with
be sequences with  and
and  . Then for
. Then for  it follows that:
it follows that:
Informally: Sums, differences and products of convergent sequences are convergent.
Part 1. Let  . We must show, that for all
. We must show, that for all  it follows that:
it follows that:
 The left hand side we estimate using:
The left hand side we estimate using:

Because  and
and  converge, for each given
converge, for each given  it holds true that:
it holds true that:

Therefore
 for all numbers
for all numbers  . Therefore the sequence
. Therefore the sequence
 is a zero sequence and the desired inequality is shown.
is a zero sequence and the desired inequality is shown.
Part 2. Let  . We have to show, that for all
. We have to show, that for all 
 Furthermore an estimation of the left hand side follows:
Furthermore an estimation of the left hand side follows:
 We choose a number
We choose a number  , such that
, such that  for all
for all  and
and  . Such a value of
. Such a value of  exists by the Theorem of convergent sequences being bounded. We can then use the estimation:
exists by the Theorem of convergent sequences being bounded. We can then use the estimation:
 For all
For all  we have
we have  and
and  , and - putting everything together - the desired inequality it shown.
, and - putting everything together - the desired inequality it shown.
 '; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
/* fibonacci sequence */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox : [-1, 40, 10, -5 ],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
straightFirst : false, highlight : false,
drawZero : true,
ticks : { drawLabels : false, minorTicks : 0, majorHeight : 15, label : { highlight : false, offset : [0, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
straightFirst : false, highlight : false,
ticks : { minorTicks : 0, majorHeight : 15, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 5; };
var a_k = [1, 1];
var newbar = function(k) {
var y;
if(k-1 > a_k.length-1) {
y = a_k[k-3] + a_k[k-2];
a_k.push(y);
} else {
y = a_k[k-1];
}
return board.create('polygon', [[k-1/4, 0], [k+1/4, 0], [k+1/4, y], [k-1/4, y]] , {
vertices : { visible : false },
borders : { strokeColor : 'black', strokeOpacity : .6, highlight : false },
fillColor : '#b2caeb',
fixed : true,
highlight : false
});
}
var bars = [];
for(var i=0; i < 9; i++) {
const k = i+1;
board.create('text', [k-.1, -.6, function() { return '
'; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
/* fibonacci sequence */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox : [-1, 40, 10, -5 ],
axis : false,
shownavigation : false,
showcopyright : false
});
var xaxis = board.create('axis', [[0, 0], [1, 0]], {
straightFirst : false, highlight : false,
drawZero : true,
ticks : { drawLabels : false, minorTicks : 0, majorHeight : 15, label : { highlight : false, offset : [0, -15] } }
});
var yaxis = board.create('axis', [[0, 0], [0, 1]], {
straightFirst : false, highlight : false,
ticks : { minorTicks : 0, majorHeight : 15, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } }
});
xaxis.defaultTicks.ticksFunction = function() { return 1; };
yaxis.defaultTicks.ticksFunction = function() { return 5; };
var a_k = [1, 1];
var newbar = function(k) {
var y;
if(k-1 > a_k.length-1) {
y = a_k[k-3] + a_k[k-2];
a_k.push(y);
} else {
y = a_k[k-1];
}
return board.create('polygon', [[k-1/4, 0], [k+1/4, 0], [k+1/4, y], [k-1/4, y]] , {
vertices : { visible : false },
borders : { strokeColor : 'black', strokeOpacity : .6, highlight : false },
fillColor : '#b2caeb',
fixed : true,
highlight : false
});
}
var bars = [];
for(var i=0; i < 9; i++) {
const k = i+1;
board.create('text', [k-.1, -.6, function() { return ' '; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
'; }], {
useMathJax : true,
strokeColor : '#2183de',
fontSize : 13,
fixed : true,
highlight : false
});
board.fullUpdate();
})();
'; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
board.create('point', [i, 1/i], {
size : 4,
name : '',
strokeWidth : .5,
strokeColor : 'black',
face : 'diamond',
fillColor : '#cf4490',
fixed : true
});
}
board.fullUpdate();
})();
'; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
'; }], {
useMathJax : true,
strokeColor : '#2183de',
fontSize : 13,
fixed : true,
highlight : false
});
board.fullUpdate();
})();
'; }], {
useMathJax : true,
fixed : true,
strokeOpacity : 0.6
});
board.create('point', [i, 1/i], {
size : 4,
name : '',
strokeWidth : .5,
strokeColor : 'black',
face : 'diamond',
fillColor : '#cf4490',
fixed : true
});
}
board.fullUpdate();
})();







































































