Previous
Next

5. Electrical double layer and adsorption

5.3. Gouy-Chapman model

The classic Gouy-Chapman model describes the layer between the outer Helmholtz plane and the bulk of the solution. In this layer, the charges are assumed to be point charges and the solution is a medium without a structure described by the relative permittivity \( \varepsilon \)r. Since the only thing that matters is the potential difference, the potential of the bulk solution can be assumed to be zero and the potential of the Helmholtz plane is denoted \( \phi \)2. Let us leave the inner layer for a moment and take a closer look at the diffuse layer.

 

The total charge density r(x) is obtained from electrostatics using the Poisson equation:

\( \displaystyle\rho(x)=-\varepsilon_r\varepsilon_0\frac{d^2\phi}{dx^2} \)                                                                           (5.33)

On the other hand, the charge density can be expressed as the sum of all ions present in the diffuse layer:

\( \displaystyle\rho(x)=\sum_iz_iFc_i(x)\)                                                                                                                                  (5.34)

The ions in the double layer follow the Boltzmann distribution:

\( \displaystyle c_i(x)=c_i^b\exp\left(-\frac{z_iF\phi}{RT}\right) \)                                                                                           (5.35)

Combing the two equations, we get the Poisson-Boltzmann differential equation:

\( \displaystyle\frac{d^2\phi}{dx^2}=-\frac{F}{\varepsilon_r\varepsilon_0}\sum\limits_iz_ic_i^b\exp\left(-\frac{z_iF\phi}{RT}\right) \)
 (5.36)

Intergration by substitution gives

\(\displaystyle \frac{d\phi}{dx}=p \Rightarrow \frac{d^2\phi}{dx^2}=\frac{dp}{dx}=\frac{dp}{d\phi}\frac{d\phi}{dx}=p\frac{dp}{d\phi} \) (5.37)

Thus

 \( \displaystyle\int pdp=-\frac{F}{\varepsilon_r\varepsilon_0}\int\sum\limits_iz_ic_i^b\exp\left(-\frac{z_iF\phi}{RT}\right)d\phi \)

  (5.38)
\( \displaystyle\frac{1}{2}\left(\frac{d\phi}{dx}\right)^2=\frac{RT}{\varepsilon_r\varepsilon_0}\sum\limits_iz_ic_i^b\exp\left(-\frac{z_iF\phi}{RT}\right)+B \) (5.39)

The integration constant B can be determined with the help of the following boundary conditions: The electric field must vanish in the bulk solution, and thus this symmetry requirement results in a boundary condition d\( \phi \)/dx = 0. According to the electroneutrality condition, the net charge of the bulk must also be zero, and therefore \( \phi \) = 0. Equation (5.39) therefore becomes

\( \displaystyle\frac{1}{2}\left(\frac{d\phi}{dx}\right)^2=\frac{RT}{\varepsilon_r\varepsilon_0}\sum\limits_iz_ic_i^b\left[\exp\left(-\frac{z_iF\phi}{RT}\right)-1\right] \) (5.40)

Consider a symmetrical electrolyte, e.g. NaCl (1:1) or CaCO3 (2:2). Equation (5.40) becomes now

 \( \displaystyle\left(\frac{d\phi}{dx}\right)^2=\frac{2RTc^b}{\varepsilon_r\varepsilon_0}\left[\exp\left(\frac{-zF\phi}{RT}\right)+\exp\left(\frac{zF\phi}{RT}\right)-2\right]=\frac{8RTc^b}{\varepsilon_r\varepsilon_0}\sinh^2\left(\frac{zF\phi}{2RT}\right) \)

  (5.41)
\( \displaystyle\Rightarrow \frac{d\phi}{dx} =-\left(\frac{8RTc^b}{\varepsilon_r\varepsilon_0}\right)^{1/2}\sinh\left(\frac{zF\phi}{2RT}\right) \) (5.42)

Note that we need to choose the negative root for (d\( \phi \)dx)! The equation can be integrated in a closed form, and after some slightly tedious algebra, the solution becomes

\( \displaystyle\frac{\tanh(zF\phi/4RT)}{\tanh(zF\phi_0/4RT)}=\exp(-\kappa x) \)                                                                   (5.43)

where \( \phi \)0 is potential at the electrode surface (x = 0) and

\( \displaystyle\kappa=\left(\frac{2c^bz^2F^2}{\varepsilon_r\varepsilon_0RT}\right)^{1/2} \)                                            (5.44)

is again the Debye length (see also Equation (2.33)). The potential profile (5.43) is not very illustrative and because of that, the tanh terms are usually linearized, tanh(x) ≈ x. The linearized result is simply

\( \displaystyle\phi(x)=\phi_0e^{-\kappa x} \) (5.45)


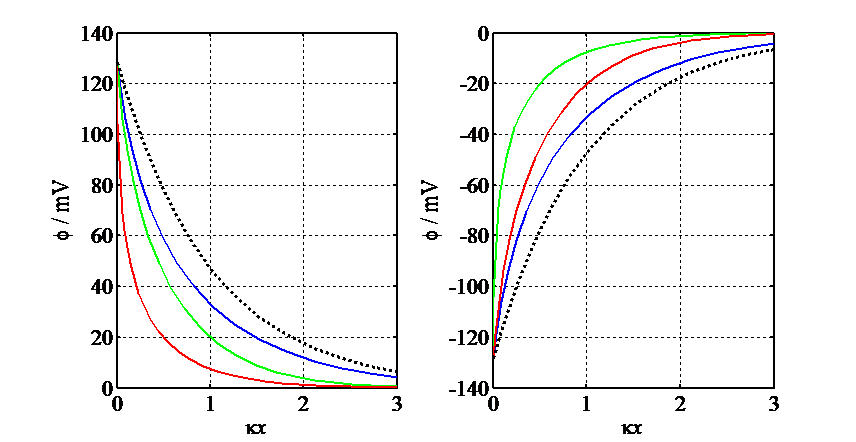
Simulated potential profiles according to Gouy-Chapman theory.

Figure 5.4. Simulated potential profiles according to Gouy-Chapman theory, F\( \phi \)0/RT = ±5: 1:1 electrolyte (blue), 2:1 electrolyte (green), 1:2 electrolyte (red). The black broken line describes the linearized equation (5.44). When \( \phi \)0 > 0, the curve for the 2:2 electrolyte almost merges with the curve for the 1:2 electrolyte (red) and when \( \phi \)0 < 0, the curve for the 2:1 electrolyte (green). Note the order of the curves with respect to \( \phi \)0.


The potential profiles are shown in Figure 5.4, including for the unsymmetrical electrolytes obtained by integrating Equation (5.40) numerically.  In Figure 5.4, \( \kappa \) = (2cbF2/\( \varepsilon \)r\( \varepsilon \)0RT)1/2.

In aqueous solution at 25 ºC, the Debye length is \( \kappa \)–1 ≈ 10–9 (z2cb)–1/2(mol/cm)1/2. A good rule of thumb is that in 1.0 mM solution, for 1:1 electrolyte \( \kappa \)–1 ≈ 10 nm.

According to Gauss's law, the charge q inside the volume V is

\( \displaystyle q=\varepsilon_r\varepsilon_0 \oint{E} \cdot dS \)                                                                                       (5.46)

where E is the electric field through a surface S. In our one-dimensional case, the scalar product E·dS is zero at all points except on the electrode surface, where it is (d\( \phi \)/dx)0dS. The charge density of the double layer is therefore

\( \displaystyle q=\varepsilon_r\varepsilon_0\left(\frac{d\phi}{dx}\right)_0 \)
                                                                     (5.47)

The charge density of the electrode for a symmetrical electrolyte is

\( \displaystyle\sigma^m=-q=(8RTc^b\varepsilon_r\varepsilon_0)^{1/2}\sinh\left(\frac{zF\phi_0}{2RT}\right) \)
              (5.48)

The differential capacitance of the electrode therefore becomes

\( \displaystyle C_d=\frac{\partial\sigma^m}{\partial\phi_0}=\left(\frac{2c^bz^2F^2\varepsilon_r\varepsilon_0}{RT}\right)^{1/2}\cosh\left(\frac{zF\phi_0}{2RT}\right) \)
 (5.49)

The scaled differential capacitances are shown in Figure 5.5, including for the unsymmetrical electrolytes. Even though the potential profiles cannot be determined in a closed form, the capacitances can be calculated using Equations (5.40) and (5.47).

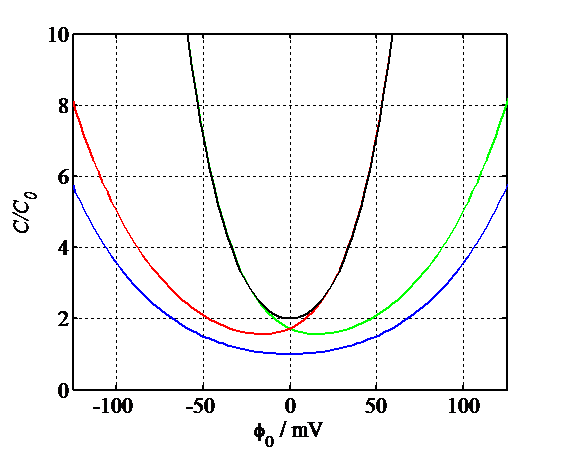
Simulated capacitances according to Gouy-Chapman theory.

Figure 5.5. Simulated capacitances according to Gouy-Chapman theory: 1:1 electrolyte (blue), 2:1 electrolyte (green), 1:2 electrolyte (red), 2:2 electrolyte (black).

 

The scaled capacitances for 1:1 electrolytes are:

\( \displaystyle C_d/C_0=\cosh(\varphi_0/2) \)
                                                                                                                       (5.50a)

For a 2:1 electrolyte:

\( \displaystyle\frac{C_d}{C_0}=\frac{e^{\varphi_0}-e^{-2\varphi_0}}{\sqrt{2e^{\varphi_0}-3+e^{-2\varphi_0}}} \)          (5.50b)

For a 1:2 electrolyte:

\( \displaystyle\frac{C_d}{C_0}=\frac{e^{2\varphi_0}-e^{-\varphi_0}}{\sqrt{e^{2\varphi_0}-3+2e^{-\varphi_0}}} \)          (5.50c)

And for a 2:2 electrolyte:
 \( \displaystyle C_d/C_0=2\cosh(\varphi_0) \)

  (5.50d)
\( \displaystyle C_0=\left(\frac{2F^2c^b\varepsilon_0\varepsilon_r}{RT}\right)^{1/2} \)    ;    \( \varphi=\frac{\phi}{RT} \)
    (5.51)

Previous
Next