MS-A0211 - Differential and Integral Calculus 2, Lecture, 10.1.2023-20.2.2023
This course space end date is set to 20.02.2023 Search Courses: MS-A0211
Lecture 11 - 14.2.2023
Completion requirements
In this lecture we studied:
In this lecture we studied:
- Surface area. We derived the formula for the surface area of parametric surfaces. For that, we cut the surfaces into small pieces and, then, each piece was approximated by a parallelogram that is a piece of the tangent plane (this is completely analogous to how we found the arc length of a curve by using small pieces of the tangent line). The area of the parallelogram is the magnitude of the cross product of tangent vectors, that are the partial derivatives of the parametric equation. Finally, the surface area is the double integral of this quantity. Then, we considered the special case when the surface is the graph of a function f(x,y). We did an example.
- Triple integrals. We gave the definition of the triple integral
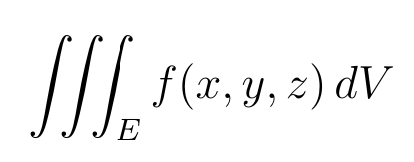
and we stated some applications: determine the volume of E by considering f(x,y,z)=1 and determine the mass of E, when f(x,y,z) is the density function.
- Fubini's Theorem. We stated Fubini's theorem for functions of three variables, which enables us to compute a triple integral by computing an iterated integral. For double integrals there are two possible orders of integration: dxdy and dydx. But there are 6 possible orders of integration for a triple integral. We did an example.
- Triple integrals over general domains. We can also integrate over general (non-rectangular box) regions. We did an example of changing the order of integration in a triple integral.
- Change of variables. We discussed changes of variables in general and that the change in volume of a small piece (i.e., dV) is given by multiplication by the absolute value of the determinant of the Jacobian matrix (as in the two variable case). In the next lecture, we will study two important particular cases: cylindrical and spherical coordinates.
