Topic outline

  • General


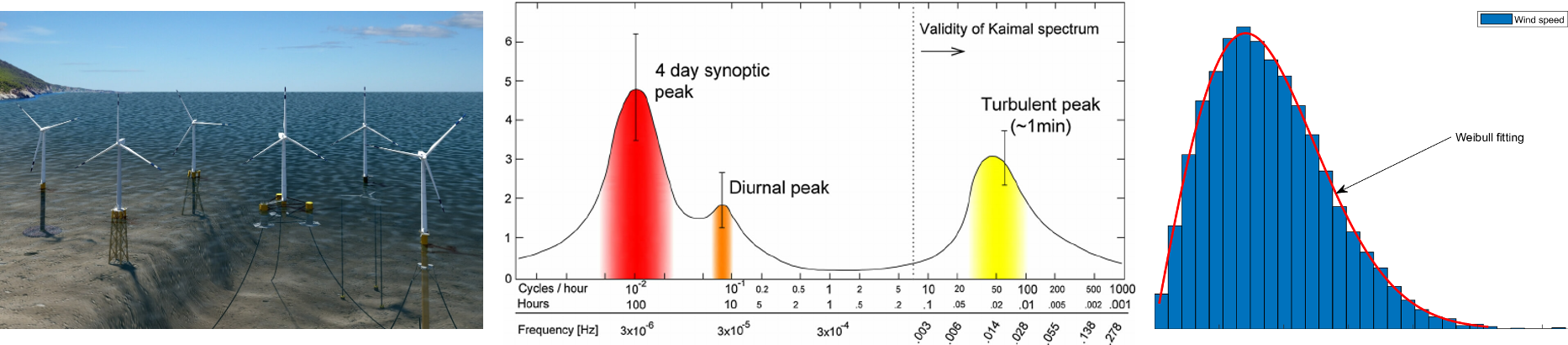
    This fully on-line course aims to introduce the students to the theoretical treatment of random (stochastic) processes such as loads due to wave, wind and road profile on structures and systems. We aim to give the student the basic knowledge of probability concepts and how they are applied in mechanics when random excitation and response to it are assessed. For this, we need to give information of the random variables and how various probability distributions are connected. Then we need to learn to use the tools to apply time-domain measurements and convert them to frequency domain where we define the load spectrum (spectral analysis). These methods are used to estimate the probability of exceedance of certain load from the load spectrum (extreme values, or long term cumulative fatigue loading). 

    The course utilizes problem-based-learning concept. Each week (check left margin for details) we define a subtask to be solved, which is complemented with video lectures, question hours (Zoom-link) and supporting articles and references to certain text books. Then the students will work on personal learning diaries (which replaces the course exam, thus you can select between these weekly personal submissions and the final exam at the end of the course) and group assignments and submit them for review when completed. Within few days, the students receive their graded reports and proposals for corrections that can raise the grade. The corrections are due within one week from the feedback. Then the corrected submission will be graded and this grade contributes directly to the course grade. The grading of personal and group works are described in details in Learning Diaries and Assignments sections. The strict grade boundaries are:

    <50%=0

    50%=1

    60%=2

    70%=3

    80%=4

    90%=5

    After the course, the you can identify, categorize, analyze and synthesize the random loads for selected engineering application, that means:

    1. Identification of the problem from the mission,

    2. Characterization of the environment through spectra and probability distributions,

    3. Analyzing the response for random excitation by using linearity assumption in the process,

    4. Definition of the short and long term responses and related statistics (for ultimate limit states and fatigue). 

    For any inquiries, please contact the course teacher(s) mashrura.musharraf@aalto.fi and jani.romanoff@aalto.fi