Differential and Integral Calculus: Elementary functions

6. Elementary functions

Table of Content

Functions
Inverse functions
Transcendental functions

This chapter gives some background to the concept of a function. We also consider some elementary functions from a (possibly) new viewpoint. Many of these should already be familiar from high school mathematics, so in some cases we just list the main properties.

Functions

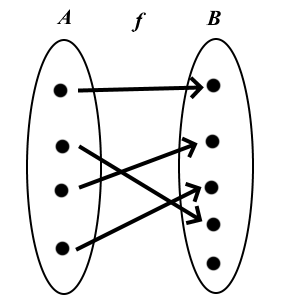
Definition: Function

A function $f\colon A\to B$ is a rule that determines for each element $a\in A$ exactly one element $b\in B$ . We write $b=f(a)$ .

Definition: Domain and codomain

In the above definition of a function $A=D_f$ is the domain (of definition) of the function $f$ and $B$ is called the codomain of $f$ .

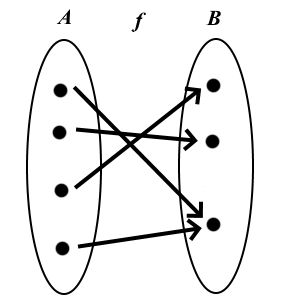
Definition: Image of a function

The image of $f$ is the subset $f[A]= \{ f(a) \mid a\in A\}$ of $B$ . An alternative name for image is range.

For example, $f\colon \mathbb{R}\to\mathbb{R}$ , $f(x)=x^2$ , has codomain $\mathbb{R}$ , but its image is $f[\mathbb{R} ] =[0,\infty[$ .

The function in the previous example can also be defined as $f\colon \mathbb{R}\to [0,\infty[$ , $f(x)=x^2$ , and then the codomain is the same as the image. In principle, this modification can always be done, but it is not reasonable in practice.

Example: Try to do the same for $f\colon \mathbb{R}\to\mathbb{R}$ , $f(x)=x^6+x^2+x$ , $x\in\mathbb{R}$ .

If the domain $A\subset \mathbb{R}$ then $f$ is a function of one (real) variable: the main object of study in this course.
If $A\subset \mathbb{R}^n$ , $n\ge 2$ , then $f$ is a function of several variables (a multivariable function)

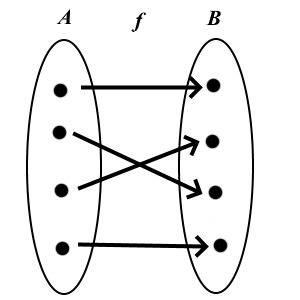
Inverse functions

Definition: Injection, surjection and bijection

A function

$f\colon A \to B$ is

injective (one-to-one) if it has different values at different points; i.e. $x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2),$ or equivalently $f(x_1)= f(x_2) \Rightarrow x_1=x_2.$
surjective (onto) if its image is the same as codomain, i.e. $f[A]=B$
bijective (one-to-one and onto) if it is both injective and surjective.

Observe: A function becomes surjective if all redundant points of the codomain are left out. A function becomes injective if the domain is reduced so that no value of the function is obtained more than once.

Another way of defining these concepts is based on the number of solutions to an equation:

Definition

For a fixed $y\in B$ , the equation $y=f(x)$ has

at most one solution $x\in A$ if $f$ is injective
at least one solution $x\in A$ if $f$ is surjective
exactly one solution $x\in A$ if $f$ on bijective.

Definition: Inverse function

If $f\colon A \to B$ is bijective, then it has an inverse $f^{-1}\colon B \to A$ , which is uniquely determined by the condition $y=f(x) \Leftrightarrow x = f^{-1}(y).$

The inverse satisfies $f^{-1}(f(a))=a$ for all $a\in A$ and $f(f^{-1}(b))=b$ for all $b\in B$ .

The graph of the inverse is the mirror image of the graph of $f$ with respect to the line $y=x$ : A point $(a,b)$ lies on the graph of $f$ $\Leftrightarrow$ $b=f(a)$ $\Leftrightarrow$ $a=f^{-1}(b)$ $\Leftrightarrow$ the point $(b,a)$ lies on the graph of $f^{-1}$ . The geometric interpretation of $(a,b)\mapsto (b,a)$ is precisely the reflection with respect to $y=x$ .

If $A \subset \mathbb{R}$ and $f\colon A\to \mathbb{R}$ is strictly monotone, then the function $f\colon A \to f[A]$ has an inverse.

If here $A$ is an interval and $f$ is continuous, then also $f^{-1}$ is is continuous in the set $f[A]$ .

Theorem: Derivative of the inverse

Let $f\colon \, ]a,b[\, \to\, ]c,d[$ be differentiable and bijective, so that it has an inverse $f^{-1}\colon \, ]c,d[\, \to\, ]a,b[$ . As the graphs $y=f(x)$ and $y=f^{-1}(x)$ are mirror images of each other, it seems geometrically obvious that also $f^{-1}$ is differentiable, and we actually have $\left(f^{-1}\right)'(x)=\frac{1}{f'(f^{-1}(x))},$ if $f'(f^{-1}(x))\neq 0$ .

Proof.

Differentiate both sides of the equation \begin{align} f(f^{-1}(x)) &= x \\ \Rightarrow f'(f^{-1}(x))\left(f^{-1}\right)'(x) &= Dx = 1, \end{align} and solve for $\left(f^{-1}\right)'(x)$ .

$\square$

Note. $f'(f^{-1}(x))$ is the derivative of $f$ at the point $f^{-1}(x)$ .

1. $f\colon A\to B$ is **one-to-one** but not **onto**

1. $f\colon A\to B$ is **one-to-one** but not **onto**

2. $f\colon A\to B$ is **onto** but not **one-to-one**

3. $f\colon A\to B$ is **one-to-one and onto**

Transcendental functions

Trigonometric functions

Unit of measurement of an angle = rad: the arclength of the arc on the unit circle, that corresponds to the angle.
$\pi$ rad = $180$ degrees, i.e. $1$ rad = $180/\pi \approx 57,\! 3$ degrees
The functions $\sin x, \cos x$ are defined in terms of the unit circle so that $(\cos x,\sin x)$ , $x\in [0,2\pi]$ , is the point on the unit circle corresponding to the angle $x\in\mathbb{R}$ , measured counterclockwise from the point $(1,0)$ . $\tan x = \frac{\sin x}{\cos x}\ (x\neq \pi /2 +n\pi),$ $\cot x = \frac{\cos x}{\sin x}\ (x\neq n\pi)$
Periodicity: $\sin (x+2\pi) = \sin x,\ \cos (x+2\pi)=\cos x,$ $\tan (x+\pi) = \tan x$

Basic properties (from the unit circle!)

$\sin 0 = 0$ , $\sin (\pi/2)=1$
$\cos 0=1$ , $\cos (\pi/2)= 0$
Parity: $\sin$ and $\tan$ are odd functions, $\cos$ is an even function: $\sin (-x) = -\sin x,$ $\cos(-x) = \cos x,$ $\tan (-x) = -\tan x.$
$\sin^2 x + \cos^2 x = 1$ for all $x\in\mathbb{R}$
Proof: Pythagorean Theorem.
Addition formulas:
$\sin (x+y) = \sin x \cos y +\cos x \sin y$

$\cos (x+y) = \cos x \cos y -\sin x \sin y$

Proof: Geometrically, or more easily with vectors and matrices.

Derivatives: $D(\sin x) = \cos x,\ \ D(\cos x) = -\sin x$

Interactivity. The connection between the unit circle and the trigonometric functions.

Example

It follows that the functions $y(t)=\sin (\omega t)$ and $y(t)=\cos (\omega t)$ satisfy the differential equation $y''(t)+\omega^2y(t)=0,$ that models harmonic oscillation. Here $t$ is the time variable and the constant $\omega>0$ is the angular frequency of the oscillation. We will see later that all the solutions of this differential equation are of the form $y(t)=A\cos (\omega t) +B\sin (\omega t),$ with $A,B$ constants. They will be uniquely determined if we know the initial location $y(0)$ and the initial velocity $y'(0)$ . All solutions are periodic and their period is $T=2\pi/\omega$ .

Harmonic oscillator $y(t) = y_{0}\cos(\omega t)$ ,
where $t$ is the elapsed time in seconds

Harmonic oscillator $y(t) = y_{0}\cos(\omega t)$ ,
where $t$ is the elapsed time in seconds

Arcus functions

The trigonometric functions have inverses if their domain and codomains are chosen in a suitable way.

The Sine function $\sin \colon [-\pi/2,\pi/2]\to [-1,1]$ is strictly increasing and bijective.
The Cosine function $\cos \colon [0,\pi] \to [-1,1]$ is strictly decreasing and bijective.
The tangent function $\tan \colon ]-\pi/2,\pi/2[\, \to \mathbb{R}$ is strictly increasing and bijective.

Arcus functions

Inverses: $\arctan \colon \mathbb{R}\to \ ]-\pi/2,\pi/2[,$ $\arcsin \colon [-1,1]\to [-\pi/2,\pi/2],$ $\arccos \colon [-1,1]\to [0,\pi]$

This means: $x = \tan \alpha \Leftrightarrow \alpha = \arctan x \ \ \text{for } \alpha \in \ ]-\pi/2,\pi/2[$ $x = \sin \alpha \Leftrightarrow \alpha = \arcsin x \ \ \text{for } \alpha \in \, [-\pi/2,\pi/2]$ $x = \cos \alpha \Leftrightarrow \alpha = \arccos x \ \ \text{for } \alpha \in \, [0,\pi]$

Note. Values of the arcus functions should be given in radians, unless we are considering some geometrical applications.

Derivatives of the arcus functions

$D \arctan x = \frac{1}{1+x^2},\ x\in \mathbb{R} \tag{1}$ $D\arcsin x = \frac{1}{\sqrt{1-x^2}},\ -1 < x < 1 \tag{2}$ $D\arccos x = \frac{-1}{\sqrt{1-x^2}},\ -1 < x < 1 \tag{3}$

Note. The first result is very useful in integration.

Proof.

Here we will only prove the first result (1). By differentiating both sides of the equation $\tan(\arctan x)=x$ for $x\in \mathbb{R}$ : $\bigl( 1+\tan^2(\arctan x)\bigr) \cdot D(\arctan x) = D x = 1$ $\Rightarrow D(\arctan x)= \frac{1}{1+\tan^2(\arctan x)}$ $=\frac{1}{1+x^2}.$

The last row follows also directly from the formula for the derivative of an inverse.

Example

Show that $\arcsin x +\arccos x =\frac{\pi}{2}$ for $-1\le x\le 1$ .

Example

Derive the addition formula for tan, and show that $\arctan x+\arctan y = \arctan \frac{x+y}{1+xy}.$

Solutions: Voluntary exercises. The first can be deduced by looking at a rectangular triangle with the length of the hypotenuse equal to 1 and one leg of length $x$ .

Introduction: Radioactive decay

Let $y(t)$ model the number of radioactive nuclei at time $t$ . During a short time interval $\Delta t$ the number of decaying nuclei is (approximately) directly proportional to the length of the interval, and also to the number of nuclei at time $t$ : $\Delta y = y(t+\Delta t)-y(t) \approx -k\cdot y(t)\cdot \Delta t.$ The constant $k$ depends on the substance and is called the decay constant. From this we obtain $\frac{\Delta y}{\Delta t} \approx -ky(t),$ and in the limit as $\Delta t\to 0$ we end up with the differential equation $y'(t)=-ky(t)$ .

Exponential function

Definition: Euler's number

Euler's number (or Napier's constant) is defined as $e = \lim_{n\to \infty} \left( 1+\frac{1}{n}\right) ^n = 1+1+\frac{1}{2!}+\frac{1}{3!} +\frac{1}{4!} +\dots$ $\approx 2,\! 718281828459\dots$

Definition: Exponential function

The Exponential function exp: $\exp (x) = \sum_{k=0}^{\infty} \frac{x^k}{k!}= \lim_{n\to \infty} \left( 1+\frac{x}{n}\right) ^n = e^x.$ This definition (using the series expansion) is based on the conditions $\exp'(x)=\exp(x)$ and $\exp(0)=1$ , which imply that $\exp^{(k)}(0)=\exp(0)= 1$ for all $k\in\mathbb{N}$ , so the Maclaurin series is the one above.

The connections between different expressions are surprisingly tedious to prove, and we omit the details here. The main steps include the following:

Define $\exp\colon\mathbb{R}\to\mathbb{R}$ , $\exp (x) =\sum_{k=0}^{\infty}\frac{x^k}{k!}.$ This series converges for all $x\in\mathbb{R}$ (ratio test).
Show: exp is differentiable and satisfies $\exp'(x)=\exp(x)$ for all $x\in \mathbb{R}$ . (This is the most difficult part but intutively rather obvious, because in practice we just differentiate the series term by term like a polynomial.)

It has the following properties $\exp (0)=1$ , $\exp (-x)=1/\exp (x) \text{ and } \exp (x+y)=\exp (x)\, \exp(y)$ for all $x,y\in \mathbb{R}$ .

These imply that $\exp (p/q)=(\exp (1))^{p/q}$ for all rational numbers $p/q\in \mathbf{Q}$ .

By continuity $\exp (x) =(\exp (1))^x$ for all $x\in \mathbb{R}$ .

Since $\exp (1) = \sum_{k=0}^{\infty}\frac{1}{k!} =\lim_{n\to \infty} \left( 1+\frac{1}{n}\right) ^n=e,$ we obtain the form $e^x$ .

$\square$ ?

Corollary

It follows from above that $\exp\colon\mathbb{R}\to\, ]0,\infty[$ is strictly increasing, bicective, and $\lim_{x\to\infty}\exp(x) = \infty,\ \lim_{x\to-\infty}\exp(x) = 0,\ \lim_{x\to\infty}\frac{x^n}{\exp (x)} = 0 \text{ for all } n\in \mathbf{N}.$

From here on we write $e^x=\exp(x)$ . Properties:

for all

$x,y\in \mathbb{R}$ .

Differential equation $y'=ky$

Theorem

Let $k\in\mathbb{R}$ be a constant. All solutions $y=y(x)$ of the ordinary differenial equation (ODE) $y'(x)=ky(x),\ x\in \mathbb{R},$ are of the form $y(x)=Ce^{kx}$ , where $C$ is a constant. If we know the value of $y$ at some point $x_0$ , then the constant $C$ will be uniquely determined.

Proof.

Suppose that $y'(x)=ky(x)$ . Then $D(y(x)e^{-kx})= y'(x)e^{-kx}+y(x)\cdot (-ke^{-kx})$ $= ky(x)e^{-kx}-ky(x)e^{-kx}=0$ for all $x\in\mathbf{R}$ , so that $y(x)e^{-kx}=C=$ constant. Multiplying both sides with $e^{kx}$ we obtain $y(x)=Ce^{kx}$ .

$\square$

Euler's formula

Definition: Complex numbers

Imaginary unit $i$ : a strange creature satisfying $i^2=-1$ . The complex numbers are of the form $z=x+iy$ , where $x,y\in \mathbb{R}$ . We will return to these later.

Theorem: Euler's formula

If we substitute $ix$ as a variable in the expontential fuction, and collect real terms separately, we obtain Euler's formula $e^{ix}=\cos x+i\sin x.$

Proof.

Substitute

$x=ix$ in the definition of the exponential function and write the series as the sum of its even (

$n=2k$ ) and odd

$(n=2k+1)$ parts. Note that

$i^{2k} = (i^2)^k = (-1)^{k}$ and remember the Taylor series of the trigonometric functions.

$\square$

As a special case we have Euler's identity $e^{i\pi}+1=0$ . It connects the most important numbers $0$ , $1$ , $i$ , $e$ ja $\pi$ and the three basic operations sum, multiplication, and power.

Using $e^{\pm ix}=\cos x\pm i\sin x$ we can also derive the expressions $\cos x=\frac{1}{2}\bigl( e^{ix}+e^{-ix}\bigr),\ \sin x=\frac{1}{2i}\bigl( e^{ix}-e^{-ix}\bigr), \ x\in\mathbb{R}.$

The graphs of $\exp(x)$ and the partial sums $\displaystyle\sum_{k=0}^{n}\frac{x^{k}}{k!}$

The graphs of $\exp(x)$ and the partial sums $\displaystyle\sum_{k=0}^{n}\frac{x^{k}}{k!}$

Logarithms

Definition: Natural logarithm

Natural logarithm is the inverse of the exponential function: $\ln\colon \ ]0,\infty[ \ \to \mathbb{R}$

Note. The general logarithm with base $a$ is based on the condition $a^x = y \Leftrightarrow x=\log_a y$ for $a>0$ and $y>0$ .

Beside the natural logarithm, in applications also appear the Briggs logarithm with base 10: $\lg x = \log_{10} x$ , and the binary logarithm with base 2: ${\rm lb}\, x =\log_{2} x$ .

Usually (e.g. in mathematical software) $\log x$ is the same as $\ln x$ .

Properties of the logarithm:

$e^{\ln x} = x$ for $x>0$
$\ln (e^x) =x$ for $x\in\mathbb{R}$
$\ln 1=0$ , $\ln e = 1$
$\ln (a^b) = b\ln a$ if $a>0$ , $b\in\mathbb{R}$
$\ln (ab) = \ln a+\ln b$ , if $a,b>0$
$D\ln |x|=1/x$ for $x\neq 0$

These follow from the corresponding properties of exp.

Example

Substituting $x=\ln a$ and $y=\ln b$ to the formula

$e^xe^y =e^{x+y}$ we obtain $ab =e^{\ln a+\ln b},$

$\ln (ab) = \ln a +\ln b$

Hyperbolic functions

Definition: Hyperbolic functions

Hyperbolic sine sinus hyperbolicus $\sinh$ , hyperbolic cosine cosinus hyperbolicus $\cosh$ and hyperbolic tangent $\tanh$ are defined as $\sinh \colon \mathbb{R}\to\mathbb{R}, \ \sinh x=\frac{1}{2}(e^x-e^{-x})$ $\cosh \colon \mathbb{R}\to [1,\infty[,\ \cosh x=\frac{1}{2}(e^x+e^{-x})$ $\tanh \colon \mathbb{R}\to \ ]-1,1[, \ \tanh x =\frac{\sinh x}{\cosh x}$

Properties: $\cosh^2x-\sinh^2x=1$ ; all trigonometric have their hyperbolic counterparts, which follow from the properties $\sinh (ix)=i\sin x$ , $\cosh (ix)=\cos x$ . In these formulas, the sign of $\sin^2$ will change, but the other signs remain the same.

Derivatives: $D\sinh x=\cosh x$ , $D\cosh x=\sinh x$ .

Hyperbolic inverse functions: the so-called area functions; area and the shortening ar refer to a certain geometrical area related to the hyperbola $x^2-y^2=1$ : $\sinh^{-1}x=\text{arsinh}\, x=\ln\bigl( x+\sqrt{1+x^2}\, \bigr) ,\ x\in\mathbb{R}$ $\cosh^{-1}x=\text{arcosh}\, x=\ln\bigl( x+\sqrt{x^2-1}\, \bigr) ,\ x\ge 1$

Derivatives of the inverse functions: $D \sinh^{-1}x= \frac{1}{\sqrt{1+x^2}} ,\ x\in\mathbb{R}$ $D \cosh^{-1}x= \frac{1}{\sqrt{x^2-1}} ,\ x > 1.$

'; }], { useMathJax : true, anchor : g, fixed : true }); var s1 = board.create('segment', [[0, 0], [1, 0]], { fixed : true, highlight : false, dash : 2, strokeWidth : 2, strokeColor : 'black' }); var s2 = board.create('segment', [[0, 0], function() { return [g.X(), g.Y()]; }], { fixed : true, highlight : false, dash : 2, strokeWidth : 2, strokeColor : 'black' }); var x = board.create('angle', [s1, s2, 1, 1], { name : '

$x$ ', radius : .4, label : { useMathJax : true, strokeColor : 'black', offset : [0, .5] } }); var info = board.create('text', [-1.2, -1.25, function() { return '

$(\\cos x,\\sin x)=(' + Math.cos(x.Value()).toFixed(3) + ',' + Math.sin(x.Value()).toFixed(3) + ')$ '; }], { useMathJax : true, fixed : true }); board.fullUpdate(); })();

MS-A0109 - Differential- och integralkalkyl 1, Föreläsning, 6.9.2022-19.10.2022