MS-A0201 - Differentiaali- ja integraalilaskenta 2 (TFM), Luento-opetus, 10.1.2023-20.2.2023
Kurssiasetusten perusteella kurssi on päättynyt 20.02.2023 Etsi kursseja: MS-A0201
Differentiaali- ja integraalilaskenta 2
9. Taso- ja avaruusintegraalit
9.1. Epäoleelliset integraalit. Muuttujanvaihto taso- ja avaruusintegraaleissa
Epäoleelliset integraalit
Tähän asti integrointi on tapahtunut rajoitetussa alueessa rajoitetulle funktiolle (integrandille). Joskus voidaan kuitenkin integroida rajoittamattomia funktioita ja/tai rajoittamattomassa alueessa.
Tarkastellaan ainoastaan tapausta, jossa funktio f on ei-negatiivinen eli f(u)≥0 kaikilla u∈D. Lasketaan funktion f(x,y)=e−x2 integraali alueessa suorien y=±x rajoittamassa rajoittamattomassa alueessa D, jossa x>0. Mikäli integraali on suppenee, sen arvo saadaan laskemalla ∬De−x2dA=∫∞0∫x−xe−x2dydx=∫∞02xe−x2dx =limR→∞∫R02xe−x2dx. Integraalin laskemiseksi huomataan, että ddxe−x2=−2xe−x2. Siten limR→∞∫R02xe−x2dx=limR→∞−e−x2|Rx=0=limR→∞1−e−R2=1.
Esimerkki
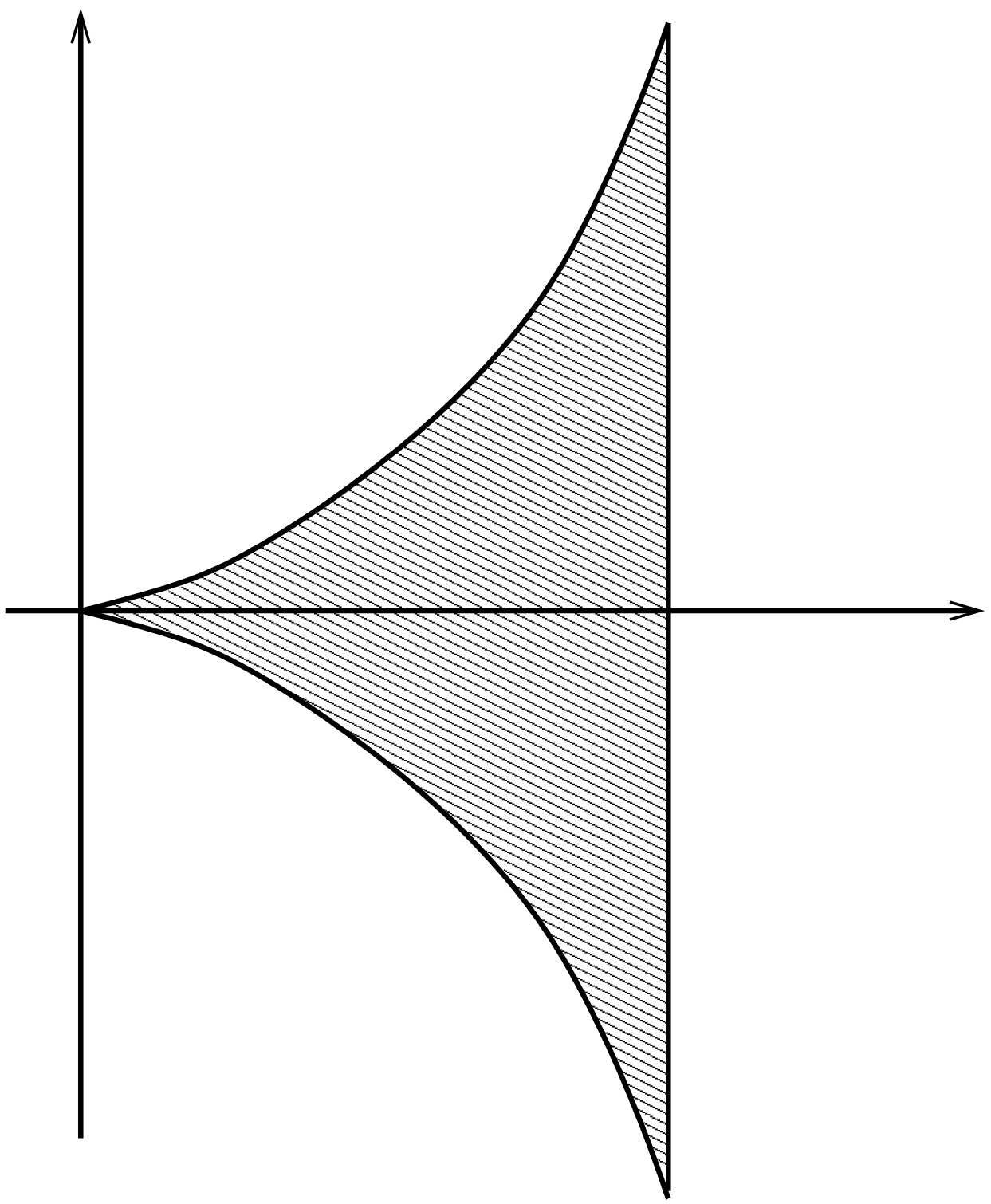
Olkoon D1={(x,)∈R2:0<x<1,|y|≤x2} ja rajoittamaton funktio f(x,y)=1/x2.
(i) Lasketaan integraali ∬D11x2dA=∫10∫x2−x21x2dydx =∫102dx=2.
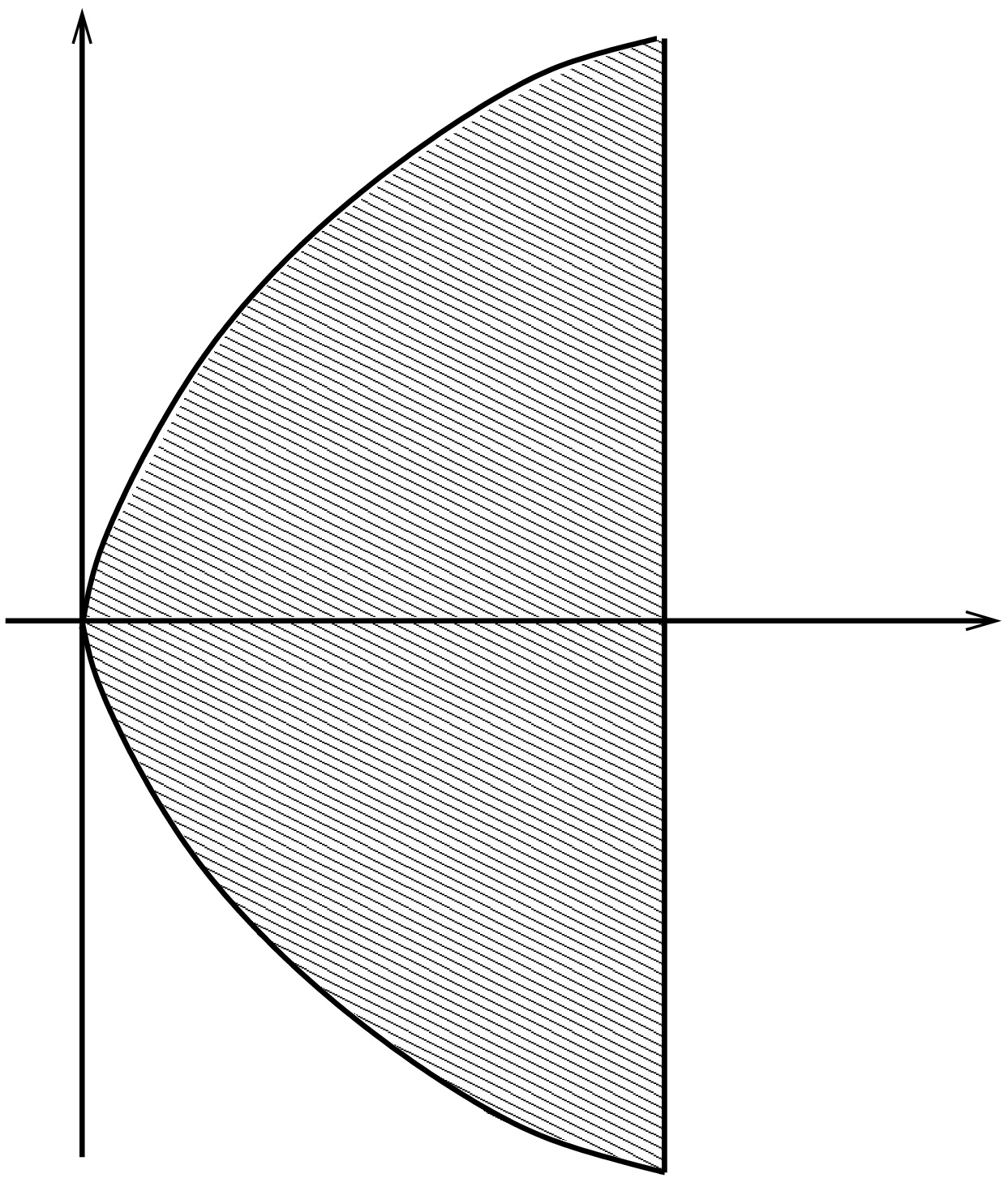
(ii) Lasketaan saman funktion integraali alueessa D2={(x,y)∈R2:0<x<1,|y|≤√x}. ∬D21x2dA=∫10∫√x−√x1x2dydx =∫102√x1x2dx=∫102x−3/2dx=limϵ→0+2x−1/2−1/2|1x=ϵ=∞. Suppeneminen riippuu integroitavan funktion lisäksi myös alueesta!
Muuttujanvaihto taso- ja avaruusintegraaleissa
Tutkitaan funktiota F:G→D, missä D ja G ovat R2:n osajoukkoja. Oletetaan, että funktion F kaikki osittaisderivaatat ovat olemassa ja jatkuvia. Lisäksi oletetaan, että F on bijektio: Jokaista pistettä (x,y)∈D vastaa yksikäsitteinen piste (u,v)∈G, jolle F(u,v)=(x,y). Tällöin erityisesti D=F(G).
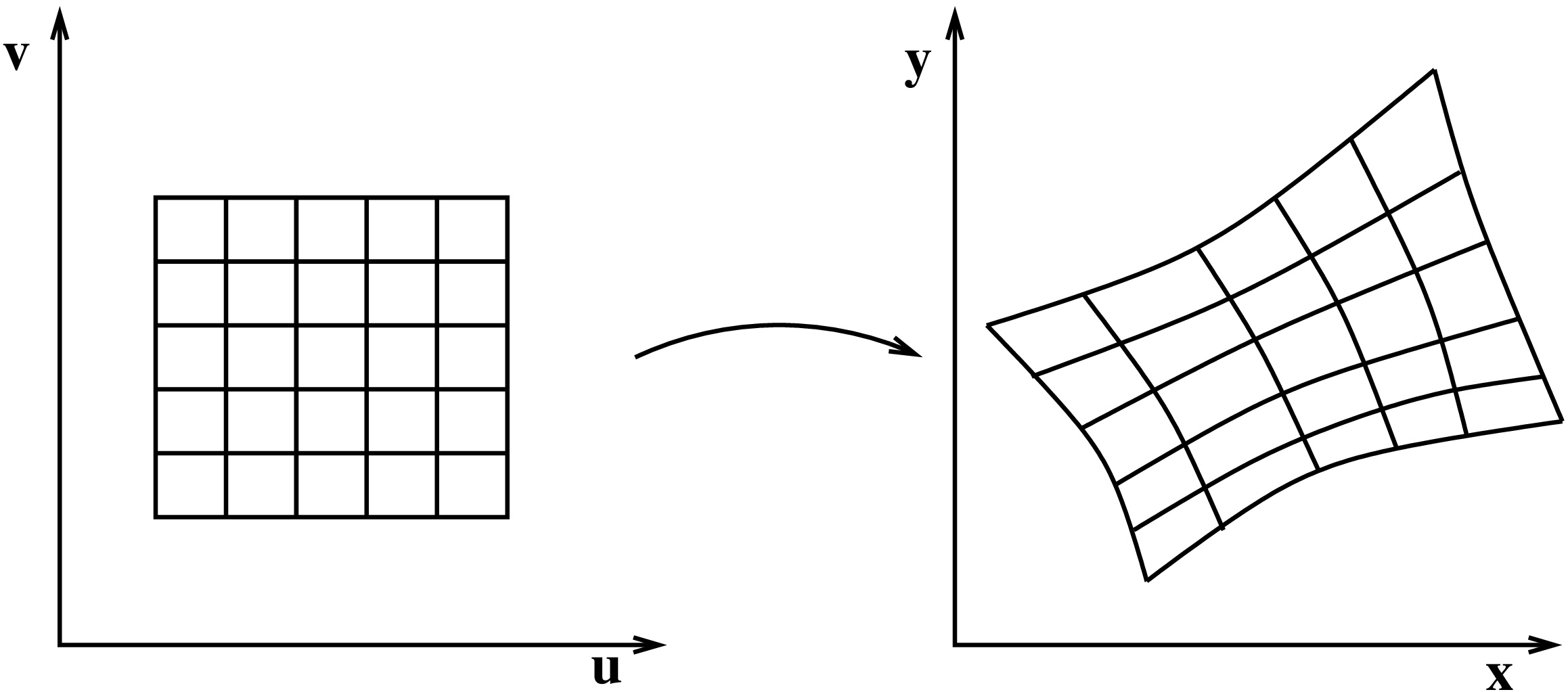
Tutkitaan aluksi muuttujanvaihtoa tasointegraalin tapauksessa: ∬Df(x,y)dxdy=∬G???dudv. Tarvitaan tieto siitä, miten pinta-ala skaalautuu funktiossa (x,y)=F(u,v).
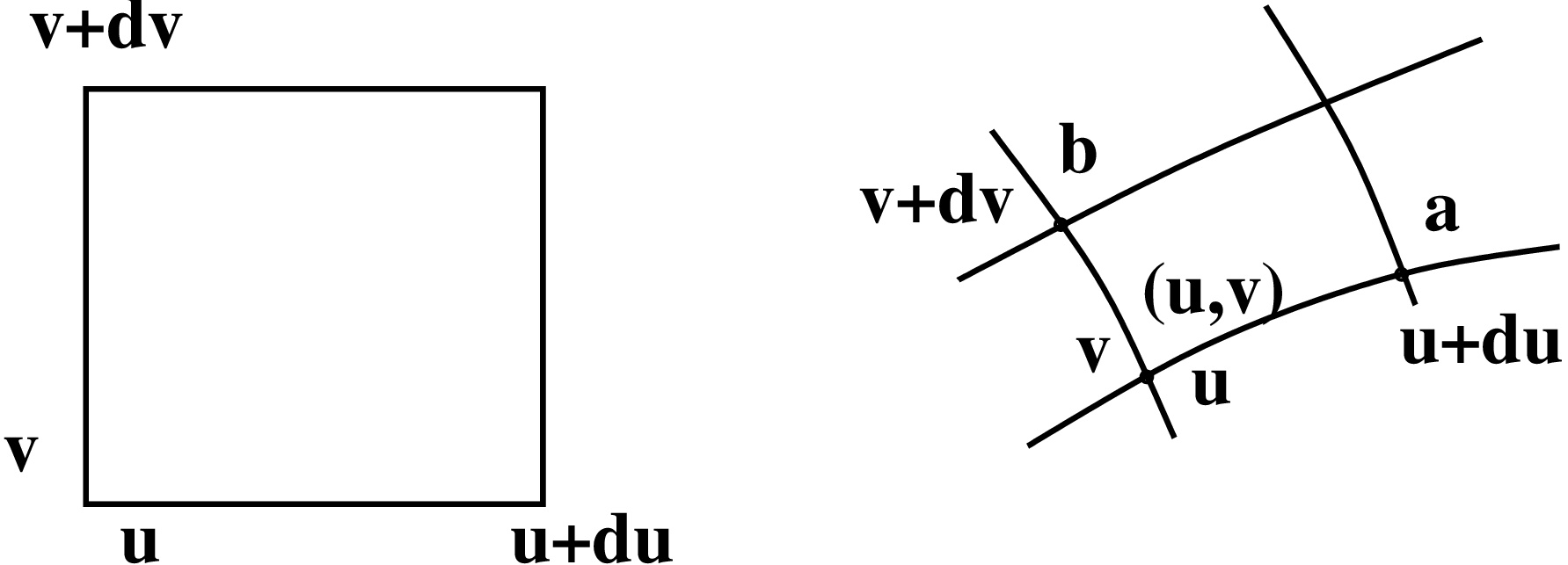
Ketjusäännöllä dx=∂x∂udu+∂x∂vdv ja dy=∂y∂udu+∂y∂vdv. Edettäessä vektorin a suuntaan (x,y)-koordinaateissa, koordinaatti v on vakio ja siten dv=0. Saadaan a≈∂x∂udui+∂y∂uduj. Samaan tapaan voidaan päätellä, että b≈∂x∂vdvi+∂y∂vdvj. Tässä i ja j ovat koordinaattiakseleiden suuntaiset yksikkövektorit.
Approksimaatiokaava pinta-alaelementin dA muutokselle siis on dA=dxdy≈|a×b|=‖ Käytetään merkintää (huom. neliömatriiseille  )
)  Determinantti
Determinantti  on funktion
on funktion  Jacobin determinantti. Sille käytetään myös merkintää
Jacobin determinantti. Sille käytetään myös merkintää 
Jacobin determinantin itseisarvo  kertoo paikallisen pinta-alan muutoksen kuvattaessa
kertoo paikallisen pinta-alan muutoksen kuvattaessa  -koordinaattien infinitesimaalinen pinta-ala
-koordinaattien infinitesimaalinen pinta-ala  vastaavalle
vastaavalle  -koordinaateissa lausutulle pinta-alalle
-koordinaateissa lausutulle pinta-alalle  funktion
funktion  välityksellä.
välityksellä.
Tasointegraalin muuttujanvaihtokaavaksi siis saadaan  missä
missä  ja
ja  . Tässä
. Tässä  on integroimisalueiden
on integroimisalueiden  ja
ja  välinen bijektio. Jacobin determinantin etumerkki kertoo, onko
välinen bijektio. Jacobin determinantin etumerkki kertoo, onko  suunnan säilyttävä vai kääntävä. Itseisarvo tarvitaan, jotta positiivisen funktion integraali ei muuttuisi negatiiviseksi eräillä
suunnan säilyttävä vai kääntävä. Itseisarvo tarvitaan, jotta positiivisen funktion integraali ei muuttuisi negatiiviseksi eräillä  .
.
Esimerkki
Lasketaan neljän paraabelin  ,
,  ,
,  ja
ja  rajoittamaan alueen
rajoittamaan alueen  pinta-ala.
pinta-ala.
Huomataan, että integroimisalue kuvautuu suorakulmioksi ![G = [1/2 , 1] \times [1/3 , 1] G = [1/2 , 1] \times [1/3 , 1]](https://mycourses.aalto.fi/filter/tex/pix.php/f1c9f915649ee6dd8d38f38afa355761.gif) muunnoksella
muunnoksella 
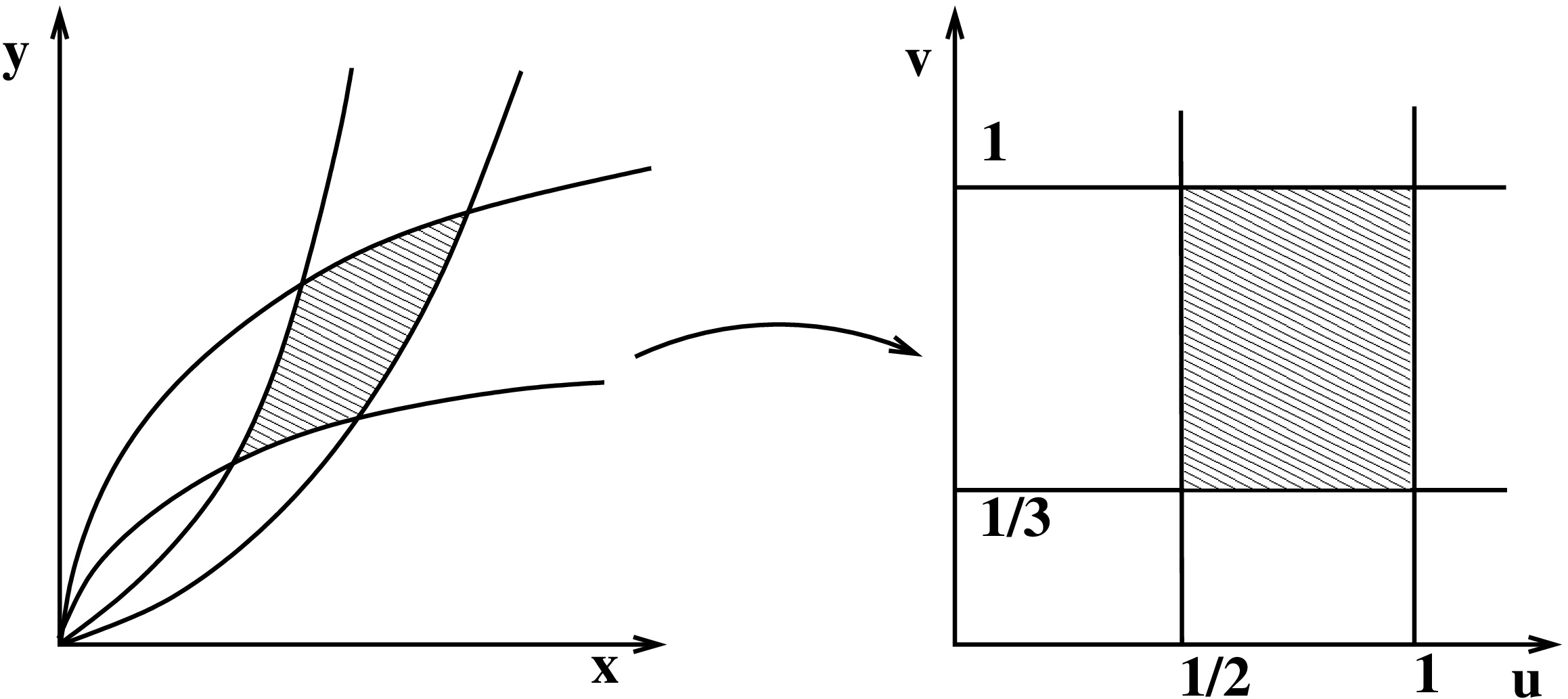
Halutaan kuitenkin käänteiskuvaus  , joka vie koordinaatit
, joka vie koordinaatit  käyräviivaisille
käyräviivaisille  -koordinaateille. Lineaarialgebran perusteella
-koordinaateille. Lineaarialgebran perusteella  Lasketaan
Lasketaan  Saadaan myös
Saadaan myös 
Lasketaan edelleen 
 Tulokseksi siis saadaan
Tulokseksi siis saadaan  Yleensä ei käy niin onnellisesti, että sama koordinaatistomuunnos vie integroitavan alueen suorakulmiolle samalla kun integroitava funktio menee vakioksi.
Yleensä ei käy niin onnellisesti, että sama koordinaatistomuunnos vie integroitavan alueen suorakulmiolle samalla kun integroitava funktio menee vakioksi.
