4. Derivaatta

Sisältö

Derivaatta

Tässä luvussa käsitellään derivaattaa ja sen ominaisuuksia. Aloitetaan esimerkillä, joka johdattelee derivaatan määritelmää.

Esimerkki 0.

Alla oleva kuvaaja kertoo, kuinka kauaksi pyöräilijä on edennyt lähtöpisteestään.


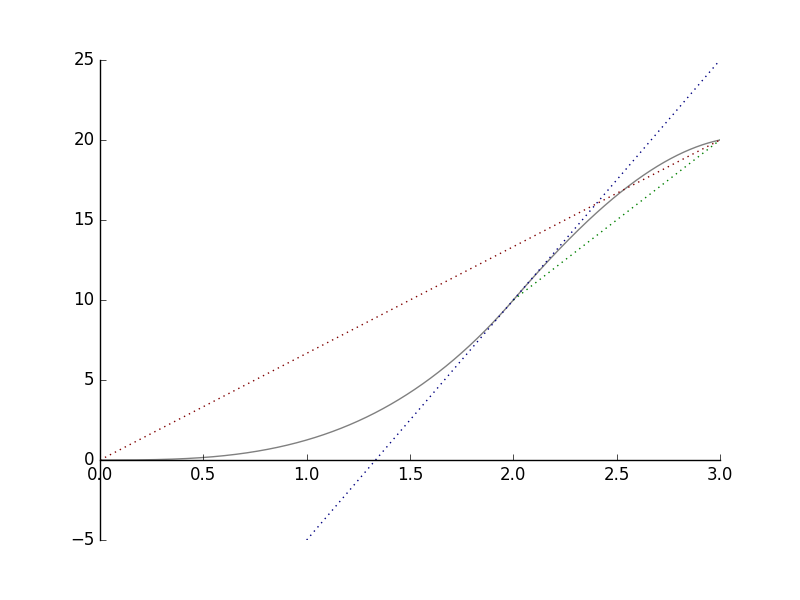
a) Tarkastellaan punaista viivaa. Huomataan, että kolmen tunnin aikana pyöräilijä on edennyt \(20\) km. Hänen keskinopeutensa on \(6{,}7\) km/h.
b) Tarkastellaan sitten vihreää viivaa. Huomataan, että kolmannen tunnin aikana pyöräilijä on edennyt \(10\) km. Tällä aikavälillä hänen keskinopeutensa on siis \(10\) km/h.
 Huomaa, että punaisen viivan kulmakerroin on \(20/3 \approx 6{,}7\) ja vihreän viivan kulmakerroin on \(10\). Lukuarvot ovat samat kuin vastaavat keskinopeudet.
c) Tarkastellaan vielä sinistä viivaa. Se on kuvaajan tangentti kohdassa \(x=2\) h. Kuten keskinopeuksien kohdalla, voidaan päätellä, että kaksi tuntia lähdön jälkeen pyöräilijän nopeus oli \(30/2\) km/h \(= 15\) km/h.

Siirrytään sitten yleiseen määritelmään:

Määritelmä: Derivaatta

Olkoon  \((a,b)\subset \mathbb{R}\). Funktion \(f\colon (a,b)\to \mathbb{R}\) derivaatta pisteessä \(x_0\in (a,b)\) on \[f'(x_0):=\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}.\] Jos \(f'(x_0)\) on olemassa, niin \(f\) on derivoituva pisteessä \(x_0\).

Huom: Koska \(x = x_0+h\), niin \(h=x-x_0\), joten määritelmä voidaan kirjoittaa myös muodossa \[f'(x_0):=\lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}.\]

Derivaatalle käytetään erilaisia merkintöjä: \[ f'(x_0)=Df(x_0) =\left. \frac{df}{dx}\right|_{x=x_0}, \ \ f'=Df =\frac{df}{dx}. \]

Tulkinta. Tarkastellaan käyrää \(y = f(x)\). Jos piirretään suora viiva pisteiden \((x_0,f(x_0))\) ja \((x_0+h, f(x_0+h))\) kautta, niin tämän suoran kulmakerroin on \[\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0} = \frac{f(x_0+h)-f(x_0)}{h}.\] Kun \(h \to 0\), tämä suora sivuaa käyrää \(y = f(x)\) pisteessä \((x_0, f(x_0))\). Tämä suora on käyrän \(y=f(x)\) tangentti pisteessä \((x_0,f(x_0))\) ja sen kulmakerroin on \[\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h},\] joka on funktion \(f\) derivaatta pisteessä \( x_0\). Tangentin yhtälö on siis muotoa \[y=f(x_0)+f'(x_0)(x-x_0).\]

Kokeile. Tutki tangentin muuttumista siirtämällä sivuamispistettä.

Esimerkki 1.

Olkoon \(f\colon \mathbb{R} \to \mathbb{R}\) määritelty kaavalla \(f(x) = x^3 + 1\). Funktion \(f\) derivaatta pisteessä \(x_0 = 1\) on \[\begin{aligned}f'(1) &=\lim_{h \to 0} \frac{f(1+h)-f(1)}{h} \\ &=\lim_{h \to 0} \frac{(1+h)^3 + 1 - 1^3 - 1}{h} \\ &=\lim_{h \to 0} \frac{1+3h+3h^2+h^3-1}{h} \\ &=\lim_{h \to 0} \frac{h(3+3h+h^2)}{h} \\ &=\lim_{h \to 0} 3+3h+h^2 \\ &= 3. \end{aligned}\]

Funktion \( f(x)=x^3 + 1\) kuvaaja ja sen tangentti pisteessä \((1,2)\).

Esimerkki 2.

Olkoon \(f\colon \mathbb{R} \to \mathbb{R}\), \(f(x)=ax+b\). Lasketaan funktion \(f\) derivaatta.

Määritelmän mukaan saadaan: \[\begin{aligned}f'(x) &=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to 0} \frac{[a(x+h)+b]-[ax+b]}{h} \\ &=\lim_{h\to 0} a \\ &=a.\end{aligned}\]

Tässä \(a\) on tangentin kulmakerroin kaikissa pisteissä. Huomaa, ettei se riipu muuttujasta \(x\), koska \(y=ax+b\) on suoran yhtälö.

Huom. Kun \(a=0\), niin \(f(x) = b\) ja \(f'(x) = 0\). Vakiofunktion derivaatta on siis nolla.

Esimerkki 3.

Olkoon \(g\colon \mathbb{R} \to \mathbb{R}\), \(g(x)=|x|\). Onko \(g\) derivoituva pisteessä \(0\)?

Nyt \[g'(x_0)= \begin{cases}+1, & \text{kun $x_{0}>0$} \\ -1, & \text{kun $x_{0}<0$}\end{cases}\]

Kuvaajalla \(y=g(x)\) ei ole tangenttia pisteessä \(x_0=0\): \[\frac{g(0+h)-g(0)}{h}= \frac{|0+h|-|0|}{h}=\frac{|h|}{h}=\begin{cases}+1, & \text{kun $h>0$}, \\ -1, & \text{kun $h<0$}.\end{cases}\] Näin ollen \(g'(0)\) ei ole olemassa.

Johtopäätös. Funktio \(g\) ei ole derivoituva pisteessä \(0\).

Huom. Olkoon \(f\colon (a,b)\to \mathbb{R}\). Jos \(f'(x)\) on olemassa kaikissa pisteissä \(x\in (a,b)\), niin saadaan uusi funktio \(f'\colon (a,b)\to \mathbb{R}\). Merkitään:

(1) \(f(x)\) = \(f^{(0)}(x)\),
(2) \(f'(x)\) =  \(f^{(1)}(x)\) =  \(\frac{d}{dx}f(x)\),
(3) \(f''(x)\) =  \(f^{(2)}(x)\) =  \(\frac{d^2}{dx^2}f(x)\),
(4) \(f'''(x)\) =  \(f^{(3)}(x)\) =  \(\frac{d^3}{dx^3}f(x)\),
...

Tässä \(f''(x)\) on funktion \(f\) toisen kertaluvun derivaatta pisteessä \(x\), \(f^{(3)}\) on kolmannen kertaluvun derivaatta jne.

Yleisesti merkitään \begin{eqnarray} C^n\bigl( ]a,b[\bigr) =\{ f\colon \, ]a,b[\, \to \mathbb{R} & \mid & f \text{ on } n \text{ kertaa derivoituva välillä } ]a,b[ \nonumber \\ & & \text{ ja } f^{(n)} \text{ on jatkuva}\}. \nonumber \end{eqnarray} Tällaiset funktiot ovat n kertaa jatkuvasti derivoituvia.

Funktion \(g(x)=|x|\) kuvaaja.

Esimerkki 4.

Pyöräilijän paikkaa kuvaa funktio \(s(t)\). Pöyräilijän nopeus hetkellä \(t\) on \(s'(t)\) ja kiihtyvyys on \(s''(t)\).

Linearisointi ja differentiaali
Derivaattaa voidaan käyttää myös funktioiden approksimoimiseen. Määritelmästä seuraa, että \[ f'(x_0)\approx \frac{f(x)-f(x_0)}{x-x_0} \Leftrightarrow f(x)\approx f(x_0)+f'(x_0)(x-x_0), \] missä oikean puolen lauseke on funktion \(f\) linearisointi tai differentiaali pisteessä \(x_0\). Differentiaalia merkitään \(df\). Linearisoinnin kuvaaja \[ y=f(x_0)+f'(x_0)(x-x_0), \] on funktion kuvaajan tangentti pisteessä \((x_0,f(x_0))\). Differentiaalin varsinainen merkitys tulee näkyviin vasta usean muuttujan funktioiden yhteydessä, eikä sitä tarvita tällä kurssilla.

Kokeile.

Derivaatan ominaisuudet

Seuraavaksi käydään läpi derivaatan tärkeimmät ominaisuudet. Näiden avulla voidaan selvittää tärkeimpien alkeisfunktioiden derivaatat.

Jatkuvuus ja derivaatta

Jos \(f\) on derivoituva pisteessä \(x_0\), niin \(f\) on jatkuva pisteessä \(x_0\): \[ \lim_{h\to 0} f(x_0+h) = f(x_0).\] Miksi? Jos \(f\) on derivoituva, niin \[f(x_0)+h\frac{f(x_0+h)-f(x_0)}{h} \rightarrow f(x_0)+0\cdot f'(x_0)=f(x_0),\] kun \(h \to 0\).

Note. Jos funktio on jatkuva pisteessä \(x_0\), ei se välttämättä ole derivoituva tässä pisteessä. Esimerkiksi \(g(x) = |x|\) on jatkuva, muttei derivoituva pisteessä \(0\).

Derivointisäännöt

Seuraavien laskusääntöjen avulla monimutkaisempien funktioiden derivaattojen laskeminen palautuu helpompiin tapauksiin.

Oletetaan, että \(f\) ja \(g\) ovat derivoituvia pisteessä \(x\).

Vakiokerroin

\[(cf)'(x) = cf'(x),\ c \in \mathbb{R}\]

Todistus.

Suppose that \(f\) is differentiable at \(x\). We determine: \[(cf)'(x),\] where \(c\in \mathbb{R}\) is a constant.

\[\begin{aligned}\frac{(cf)(x+h)-(cf)(x)}{h} \ & \ = \ \frac{cf(x+h)-cf(x)}{h} \\ & \ = \ c \ \frac{f(x+h)-f(x)}{h}\end{aligned}\]

As \(h\to 0\), we get \[c \ \frac{f(x+h)-f(x)}{h} \to c f'(x).\]

\(\square\)

Summan derivaatta

\[(f+g)'(x) = f'(x) + g'(x)\]

Todistus.

Suppose that \(f\) and \(g\) are differentiable at \(x\). We determine \[(f+g)'(x).\]

By the definition: \[\begin{aligned}\frac{(f+g)(x+h)-(f+g)(x)}{h} \ & \ = \ \frac{[f(x+h)+g(x+h)]-[f(x)+g(x)]}{h} \\ & \ = \ \frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\end{aligned}\]

When \(h\to 0\), we get \[\frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\to \ f'(x)+g'(x)\]

\(\square\)

Tulon derivaatta

\[(fg)'(x) = f'(x)g(x) + f(x)g'(x)\]

Todistus.

Suppose that \(f,g\) and are differentiable at \(x\). We determine \[(fg)'(x).\] \[\begin{aligned}\frac{(fg)(x+h)-(fg)(x)}{h} & = \frac{f(x+h)g(x+h)-f(x)g(x)}{h} \\ & = \frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h} \\ & = \frac{f(x+h)-f(x)}{h}\ g(x+h)+f(x)\ \frac{g(x+h)-g(x)}{h}\end{aligned}\]

When \(h\to 0\), we get \[\frac{f(x+h)-f(x)}{h}g(x+h)+f(x)\frac{g(x+h)-g(x)}{h}\to f'(x)g(x)+f(x)g'(x).\]

\(\square\)

Potenssin derivaatta

\[\frac{d}{dx} x^n = nx^{n-1} \text{, } n \in \mathbb{Z}\]

Todistus.

For \( n\ge 1\) we repeteadly apply the product rule, and obtain \[\begin{aligned}\frac{d}{dx}x^n \ & = \frac{d}{dx}(x\cdot x^{n-1}) \\ & = (\frac{d}{dx}x)x^{n-1}+x\frac{d}{dx}x^{n-1} \\ & \stackrel{dx/dx=1}{=} x^{n-1}+x\frac{d}{dx}x^{n-1} \\ & = x^{n-1}+x\left( x^{n-2}+x\frac{d}{dx}x^{n-2}\right) \\ & = \ldots \\ & = \sum_{k=0}^{n-1} x^{n-1} \\ & = nx^{n-1}.\end{aligned}\]

The case of negative \( n\) is obtained from this and the product rule applied to the identity \( x^n \cdot x^{-n} = 1\).

From the power rule we obtain a formula for the derivative of a polynomial. Let \[P(x)=a_n x^{n}+a_{n-1}x^{n-1}+\ldots+ a_1 x + a_0,\] where \(n\in \mathbb{N}\). Then \[\frac{d}{dx}P(x)=na_nx^{n-1}+(n-1)a_{n-1}x^{n-2}+\ldots +2 a_2 x+a_1.\]

\(\square\)

Osamäärän derivaatta: erikoistapaus

\[\Big(\frac{1}{f}\Big)'(x) = - \frac{f'(x)}{f(x)^2} \text{, } f(x) \neq 0\]

Todistus.

Suppose that \(f\) is differentiable at \(x\) and \(f(x)\neq 0\). We determine \[(\frac{1}{f})'(x).\]

From the definition we obtain: \[\begin{aligned}\frac{(1/f)(x+h)-(1/f)(x)}{h} & = \frac{1/f(x+h)-1/f(x)}{h} \\ & = \frac{\frac{f(x)}{f(x)f(x+h)}-\frac{f(x+h)}{f(x)f(x+h)}}{h} \\ & = \frac{f(x)-f(x+h)}{h}\frac{1}{f(x)f(x+h)}\end{aligned}\]

Because \(f\) is differentiable at \(x\) we get \[\frac{f(x)-f(x+h)}{h}\frac{1}{f(x)f(x+h)}=-f'(x)/f(x)^2,\] as \(h\to 0\).

\(\square\)

Osamäärän derivaatta

\[(f/g)'(x) = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2},\ g(x) \neq 0\]

Todistus.

Suppose that \(f,g\) are differentiable at \(x\) and \(g(x)\neq 0\). Then \[\begin{aligned}(f/g)'(x) & = \Big( f \cdot \frac{1}{g}\Big) '(x) \\ & = f'(x)\frac{1}{g(x)}-f(x)\frac{g'(x)}{g(x)^2} \\ & = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}.\end{aligned}\]

\(\square\)

Kokeile. Siirrä pistettä \(x_0\) ja tutki vakiokertoimen vaikutusta käytännössä.

Esimerkki 1.

\[\frac{d}{dx}(x^{2006}+5x^3+42)=\frac{d}{dx}x^{2006}+5\frac{d}{dx}x^3+42\frac{d}{dx}1=2006x^{2005}+5\cdot 3x^2.\]

Esimerkki 2.

\[\begin{aligned}\frac{d}{dx} [(x^4-2)(2x+1)] &= \frac{d}{dx}(x^4-2) \cdot (2x+1) + (x^4-2) \cdot \frac{d}{dx}(2x + 1) \\ &= 4x^3(2x+1) + 2(x^4-2) \\ &= 8x^4+4x^3+2x^4-4 \\ &= 10x^4+4x^3-4.\end{aligned}\]

Toinen tapa: \[\frac{d}{dx} [(x^4-2)(2x+1)] = \frac{d}{dx} (2x^5 +x^4 -4x -2) = 10x^4 +4x^3 -4.\]

Funktion \( (x^4-2)(2x+1) \) kuvaaja.

Esimerkki 3.

 Alueessa \(x \neq 0\) on \[\frac{d}{dx} \frac{3}{x^3} = 3 \cdot \frac{d}{dx} \frac{1}{x^3} = -3 \cdot \frac{\frac{d}{dx} x^3}{(x^3)^2} = -3 \cdot \frac{3x^2}{x^6}= - \frac{9}{x^4}.\]

Toinen tapa: Koska\(\frac{1}{x^3} = x^{-3}\), niin \[\frac{d}{dx} \ \frac{3}{x^3} = 3 \cdot \frac{d}{dx} x^{-3} = 3 \cdot (-3x^{-4})= - \frac{9}{x^4}\]

Esimerkki 4.

\[\begin{aligned}\frac{d}{dx} \frac{x^3}{1+x^2} & = \frac{(\frac{d}{dx}x^3)(1+x^2)-x^3\frac{d}{dx}(1+x^2)}{(1+x^2)^2} \\ & = \frac{3x^2(1+x^2)-x^3(2x)}{(1+x^2)^2} \\ & = \frac{3x^2+x^4}{(1+x^2)^2}.\end{aligned}\]

Funktion \(x^3 / (1+x^2)\) kuvaaja.

Rollen lause

Jos \(f\) on derivoituva paikallisessa ääriarvokohdassa \(x_0\in \, ]a,b[\), niin \(f'(x_0)=0\).

Todistus.

The one-sided limits of the difference quotient have different signs at a local extremum. For example, for a local maximum it holds that \begin{eqnarray} \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative} }{\text{positive}}&\le& 0, \text{ when } h>0, \nonumber \\ \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative}}{\text{negative}}&\ge& 0, \text{ when } h<0 \nonumber \end{eqnarray} and \(|h|\) is so small that \(f(x_0)\) is a maximum on the interval \([x_0-h,x_0+h]\).


L'Hospitalin sääntö

Tästä säännöstä on monia eri versioita, mutta tässä käsitellään vain yksi tapaus. Oletetaan, että \(f(x_0)=g(x_0)=0\) ja että funktiot \(f,g\) ovat derivoituvia jollakin välillä \(]x_0-\delta,x_0+\delta[\). Jos \[ \lim_{x\to x_0}\frac{f'(x)}{g'(x)} \] on olemassa, niin \[ \lim_{x\to x_0}\frac{f(x)}{g(x)}=\lim_{x\to x_0}\frac{f'(x)}{g'(x)}. \]

Proof (idea).

In the special case \(g'(x_0)\neq 0\) the proof is simple: \[ \frac{f(x)}{g(x)}=\frac{f(x)-f(x_0)}{g(x)-g(x_0)} = \frac{\bigl( f(x)-f(x_0)\bigr) /(x-x_0)}{\bigl( g(x)-g(x_0)\bigr) /(x-x_0)} \to \frac{f'(x_0)}{g'(x_0)}. \] In the general case we need the so-called generalized mean value theorem, which states that \[ \frac{f(x)}{g(x)} = \frac{f'(c)}{g'(c)} \] for some \(c\in \, ]x_0,x[\). Here we have the same point \(c\) both in the numerator and the denominator, so we do not even need the continuity of the derivatives!

Trigonometristen funktioiden derivaatat

Tässä kappaleessa johdetaan funktioiden \(\sin\), \(\cos\) ja \(\tan\) derivaatat.

Sinin derivaatta

\[\sin'(t)=\cos(t)\]

Todistus.

Funktion \(\sin(x)\) ja sen derivaatan \(\cos(x)\) kuvaajat.

Kosinin derivaatta

\[\cos'(t)= - \sin(t)\]

Todistus.

This follows in a similar way as the derivative of Sine, but more easily from the identity \(\cos(t)=\sin(\pi/2-t)\) and the Chain rule to be introduced in the following section.

\(\square\)

Funktion \(\cos(x)\) ja sen derivaatan  \(-\sin(x)\) kuvaajat.

Tangentin derivaatta

\[\tan'(t) = \frac{1}{\cos^2(t)}=1+\tan^2 t.\]

Todistus.

Because \[\tan(t)=\frac{\sin(t)}{\cos(t)},\] from the quotient rule we obtain \[\tan'(t)=\frac{\sin'(t)\cos(t)-\sin(t)\cos'(t)}{\cos^2(t)}=\frac{\cos^2(t)+\sin^2(t)}{\cos^2(t)}=\begin{cases}\frac{1}{\cos^2(t)} & \\ 1+\tan^2 t.\end{cases}\]

\(\square\)

Funktion \(\tan(x)\) ja sen derivaatan \(1/\cos^2(x)\) kuvaajat.

Esimerkki 1.

\[\frac{d}{dx} (3 \sin(x)) = 3 \sin'(x) = 3 \cos(x).\]

Esimerkki 2.

\[\frac{d}{dx} \cos^2 (x) = \cos'(x) \cdot \cos(x) + \cos(x) \cdot \cos'(x) = -2\sin(x)\cos(x).\]

Esimerkki 3.

\[\begin{aligned} \frac{d}{dx} \frac{\sin(x) + 1}{\cos(x)} &= \frac{d}{dx} \left( \frac{\sin(x)}{\cos(x)} + \frac{1}{\cos(x)} \right) \\ &= \tan'(x) - \frac{\cos'(x)}{\cos^2(x)} \\ &= \frac{1+\sin(x)}{\cos^2 (x)}.\end{aligned}\]

Ketjusääntö

Ketjusäännöllä tarkoitetaan yhdistettyjen funktioiden derivoimissääntöä. Tämä termin tausta selittyy paremmin usean muuttujan funktioiden (osittais)derivaattojen yhteydessä.

Ketjusääntö.

Olkoon \(f\colon \mathbb{R}\to \mathbb{R}\), \(g\colon \mathbb{R}\to \mathbb{R}\) ja \(f \circ g \colon \mathbb{R}\to \mathbb{R}\).

Jos \(g\) on derivoituva pisteessä \(x\) ja \(f\) derivoituva pisteessä \(g(x)\), niin \[\frac{d}{dx}f(g(x))=f'(g(x))g'(x).\]

Todistus.

Consider

\[\begin{aligned}\frac{f(g(x+h))-f(g(x))}{h} &= \frac{f(g(x+h))-f(g(x))}{h} \ \frac{g(x+h)-g(x)}{g(x+h)-g(x)} \\ &= \frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)} \ \frac{g(x+h)-g(x)}{h}.\end{aligned}\]

Now let us write \(k(h):=g(x+h)-g(x)\). Then \(g(x+h)=g(x)+k(h)\) and we get \[\frac{f(g(x+h))-f(g(x))}{h}=\frac{f(g(x)+k(h))-f(g(x))}{k(h)}\frac{g(x+h)-g(x)}{h}.\]

Ongelma. Entä, jos \(k(h)=0\)? Nollalla ei voi jakaa.

Ratkaisu. Define \[E(k):= \begin{cases}0, & \text{for $k=0$}, \\ \frac{f(g(x)+k)-f(g(x))}{k}-f'(g(x)), & \text{for $k\neq 0$},\end{cases}\] so that \[\frac{f(g(x+h))-f(g(x))}{h}=[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}.\] Now, because \(E\) is continuous, we get \[[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}\to f'(g(x))g'(x).\] as \(h\to 0\).

\(\square\)

Esimerkki 1.

Lasketaan funktion \((2x-1)^3\) derivaatta. Merkitään \(f(x) = x^3\) ja \(g(x) = 2x-1\), jolloin kyseessä on yhdistetty funktio \(f(g(x))\). Koska \[f'(x) = 3x^2 \text{ ja } g'(x) = 2,\] niin \[\frac{d}{dx} (2x-1)^3 = 3(2x-1)^2 \cdot 2 = 6(4x^2-4x+1) = 24x^2-24x+6.\]

Funktion \((2x-1)^3\) ja sen derivaatan kuvaajat.

Esimerkki 2.

Lasketaan funktion \(\sin 3x\) derivaatta. Merkitään \(f(x) = \sin x\) ja \(g(x) = 3x\), jolloin kyseessä on yhdistetty funktio \(f(g(x))\). Näin ollen \[\frac{d}{dx} \sin 3x = \cos 3x \cdot 3 = 3 \cos 3x.\]

Huom. Olkoon \(h\colon \mathbb{R}\to \mathbb{R}, g\colon \mathbb{R}\to \mathbb{R}\) ja \(f\colon \mathbb{R}\to \mathbb{R}\). Tällöin \[\frac{d}{dx}f(g(h(x)))=f'(g(h(x)))\frac{d}{dx}g(h(x))=f'(g(h(x)))g'(h(x))h'(x).\] Vastaavalla tavalla saadaan monimutkaisempia kaavoja, mutta tärkeämpää on muistaa yleinen periaate.

Funktion \(\sin 3x\) ja sen derivaatan kuvaajat.

Esimerkki 3.

Lasketaan funktion \(\cos^3 2x\) derivaatta. Merkitään \(f(x) = x^3\), \(g(x) = \cos x\) ja \(h(x) = 2x\), jolloin kyseessä on yhdistetty funktio \(f(g(h(x)))\). Näin ollen \[\begin{aligned}\frac{d}{dx} \cos^3 2x &= 3(\cos 2x)^2 \cdot \frac{d}{dx} \cos 2x \\ &= 3 \cos^2 2x \cdot (-\sin 2x) \cdot 2 \\ &= -6 \sin 2x \cos^2 2x.\end{aligned}\]

Funktion \(\cos^3 2x\) ja sen derivaatan kuvaajat.

Ääriarvot

Tässä kappaleessa tarkastellaan derivaatan käyttöä ääriarvotehtävissä.

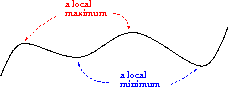
Määritelmä: Paikallinen maksimi ja minimi

Funktiolla \(f\colon A\to \mathbb{R}\) on  paikallinen maksimi pisteessä \(x_0\in A\), jos on olemassa sellainen \(h\gt 0\), että \(f(x)\leq f(x_0)\) aina kun  \(x\in A\) ja \(|x-x_0|\lt h\).

Vastaavasti, funktiolla \(f\colon A\to \mathbb{R}\) on paikallinen minimi pisteessä \(x_0\in A\) , jos on olemassa sellainen \(h>0\), että \(f(x)\geq f(x_0)\) aina kun  \(x\in A\) ja \(|x-x_0|\lt h\).

Funktion paikallinen ääriarvo tarkoittaa joko paikallista maksimia tai paikallista minimiä.

Huom. Jos \(x_0\) on paikallinen maksimikohta ja \(f'(x_0)\) on olemassa, niin \[\begin{cases}f'(x_0) & =\lim_{h\to 0^{+}}\frac{f(x_0+h)-f(x_0)}{h} \leq 0 \\ f'(x_0) & =\lim_{h\to 0^{-}}\frac{f(x_0+h)-f(x_0)}{h} \geq 0.\end{cases}\] Näin ollen \(f'(x_0)=0\).

Näin saadaan:

Lause 1.

Olkoon \(x_0\in [a,b]\) jatkuvan funktion function \(f\colon [a,b]\to \mathbb{R}\) paikallinen ääriarvokohta. Silloin joko

  1. derivaattaa \(f'(x_0)\) ei ole olemassa (tämä sisältää myös tapaukset \(x_0=a\) ja \(x_0=b\)), tai

  2. \(f'(x_0)=0\).

Esimerkki 1.

Määritellään \(f: \mathbb{R} \to \mathbb{R}\) kaavalla \[f(x) = x^3 -3x + 1.\] Silloin \[f'(x) = 3x^2-3\] ja pisteissä \(x_0 = -1\) ja \(x_0 = 1\) funktiolla \(f\) on paikallinen maksimi ja minimi, \[f'(-1) = 3 \cdot (-1)^2 - 3 = 0 \text{ ja } f'(1) = 3 \cdot 1^2 - 3 = 0.\]

Funktion \(x^3-3x+1\) ja sen derivaatan \(3x^2-3\) kuvaajat.

Globaali maksimi ja minimi

Käytännössä paikallisia ääriarvoja voi esiintyä kolmea eri tyyppiä olevissa pisteissä:

  1. derivaatan nollakohdat

  2. määrittelyvälin päätepisteet

  3. määrittelyvälin sisällä olevat kohdat, joissa funktio ei ol e derivoituva

Jos tiedetään etukäteen, että funktiolla on maksimi tai minimi, niin aluksi etsitään kaikki mahdolliset paikalliset ääriarvokohdat (yllä oleva lista), lasketaan funktion arvot näissä pisteissä ja valitaan näistä arvoista suurin tai pienin.

Esimerkki 2.

Määritetään funktion \(f\colon [0,2]\to \mathbf{R}\), \(f(x)=x^3-6x\), suurin ja pienin arvo. Koska kyseessä on suljetulla välillä jatkuva funktio, niin sillä on maksimi ja minimi. Funktio on myös derivoituva, joten riittää tutkia välin päätepisteet ja välin sisälle jäävät derivaatan nollakohdat.

Derivaatan nollakohdat: \(f'(x)=3x^2-6=0 \Leftrightarrow x=\pm \sqrt{2}\). Koska \(-\sqrt{2}\not\in [0,2]\), täytyy laskea funktion arvot vain kolmessa pisteessä: \(f(0)=0\), \(f(\sqrt{2})=-4\sqrt{2}\) ja \(f(2)=-4\). Näiden avulla päätellään funktion pienimmäksi arvoksi \(-4\sqrt{2}\) ja suurimmaksi arvoksi \(0\).

Seuraavaksi esitetään eräs tärkeimmistä derivoituvia funktioita koskevista tuloksista.

Lause 2.

(Derivoituvien funktioiden väliarvolause). Olkoon \(f\colon [a,b]\to \mathbb{R}\) jatkuva suljetulla välillä \([a,b]\) ja derivoituva avoimella välillä \((a,b)\). Silloin \[f'(x_0)=\frac{f(b)-f(a)}{b-a}\] jollekin \(x_0\in (a,b).\)

Todistus.

Let \(f\) be continuous in the interval \([a,b]\) and differentiable in the interval \((a,b)\). Let us define \[g(x):=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)-f(a).\]

Now \(g(a)=g(b)=0\) and \(g\) is differentiable in the interval \((a,b)\). According to Rolle's Theorem, there exists \(c\in(a,b)\) such that \(g'(c)=0\). Hence \[f'(c)=g'(c)+\frac{f(b)-f(a)}{b-a}=\frac{f(b)-f(a)}{b-a}.\]

\(\square\)

Tärkeitä seurauksia:

Lause 3.

Olkoon \(f\colon (a,b)\to \mathbb{R}\) derivoituva. Silloin pätee:

  1. Jos \(f'(x)\geq 0\) kaikilla \(x\in (a,b)\), niin \(f\) on kasvava,

  2. Jos \(f'(x)\leq 0\) kaikilla \(x\in (a,b)\), niin \(f\) on vähenevä.

Todistus.

Suppose that \(a \lt x_1 \lt x_2 \lt b\).

Then by Theorem 2 there exists \(x_0\in (x_1,x_2)\) such that \[f'(x_0)=\frac{f(x_2)-f(x_1)}{x_2-x_1}.\]

It follows that \(f(x_2)-f(x_1)=f'(x_0)(x_2-x_1)\).

Hence we may conclude that \(f\) is increasing for \(f'(x_0)\geq 0\) and decreasing for \(f'(x_0)\leq 0\).

Esimerkki 3.

Polynomin \(f(x) = \frac{1}{4} x^4-2x^2-7\) derivaatalle pätee  \[f'(x) = x^3-4x = x(x^2-4) = 0,\] kun \(x=0\), \(x=2\) or \(x=-2\). Muodostetaan kulkukaavio:

\(x<-2\) \(-2 \lt x \lt 0\) \(0 \lt x \lt 2\) \(x>2\)
\(x\) \(<0\) \(<0\) \(>0\) \(>0\)
\(x^2-4\) \(>0\) \(<0\) \(<0\) \(>0\)
\(f'(x)\) \(<0\) \(>0\) \(<0\) \(>0\)
\(f(x)\) väh. kasv. väh. kasv.

Funktion \(\frac{1}{4} x^4-2x^2-7\) kuvaaja.

Esimerkki 4.

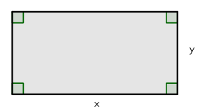
Määritetään sellainen suorakulmio, jonka pinta-ala on \(9\) ja jonka piiri on mahdollisimman pieni.

Olkoot \(x\ (>0)\) ja \(y\ (>0)\) suorakulmion sivut. Silloin \(x \cdot y = 9\), joten \(y=\frac{9}{x}\). Suorakulmion piiri on \[2x+2y = 2x+2 \frac{9}{x} = \frac{2x^2+18}{x}.\] Etsitään funktion \(f(x) = \frac{2x^2+18}{x}\) pienin arvo. Funktio \(f\) on derivoituva, kun \(x>0\), ja osamäärän derivoimissäännön mukaan \[f'(x) = \frac{4x \cdot x-(2x^2+18) \cdot 1}{x^2} = \frac{2x^2-18}{x^2}.\] Nyt \(f'(x) = 0\), kun \[\begin{aligned}2x^2-18 &= 0 \\ 2x^2 &= 18 \\ x^2 &= 9 \\ x &= \pm 3\end{aligned}\] mutta ehdon \(x>0\) perusteella vain \(x=3\) on mahdollinen. Muodotetaan kulkukaavio:

\(x<3\) \(x>3\)
\(f'(x)\) \(<0\) \(>0\)
\(f(x)\) väh. kasv.

Koska funktio \(f\) on jatkuva, niin se saavuttaa miniminsä pisteessä \(x=3\). Tällöin sen toisen sivun pituus on \(y=\frac{9}{x}=\frac{9}{3}=3\).

Vastaus on siis neliö, jonka sivun pituus on \(3\).

Funktion \(\frac{2x^2+18}{x}\) kuvaaja.

Esimerkki 5.

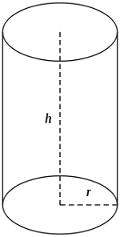
Tehtävänä on muodostaa suoran ympyräsylinterin muotoinen yhden litran mitta (ilman kantta) niin, että materiaalia tarvitaan mahdollisimman vähän.

Olkoon \(r > 0\) sylinterin poikkileikkauksen säde ja \(h > 0\) sylinterin korkeus. Sylinterin tilavuus on \(1\) dm\(^3\), joten saadaan yhtälö \(\pi r^2 h = 1\). Tästä voidaan ratkaista \[h = \frac{1}{\pi r^2}.\]

Tarvittavan materiaalin määrää kuvaa pinta-ala \[A_{\text{bottom}} + A_{\text{side}} = \pi r^2 + 2 \pi r h = \pi r^2 + \frac{2 \pi r}{\pi r^2} = \pi r^2 + \frac{2}{r}.\]

Määritellään siis \(f: (0, \infty) \to \mathbb{R}\) asettamalla \[f(r) = \pi r^2 + \frac{2}{r}.\] Tavoitteena on etsiä funktion \(f\) minimi, ja kyseessä on alueessa \(r>0\) derivoituva funktio. Derivaataksi saadaan \[f'(r) = 2\pi r -2 \cdot \frac{1}{r^2} = \frac{2\pi r^3 - 2}{r^2}.\] Nyt \(f'(r) = 0\), kun \[\begin{aligned}2\pi r^3 - 2 &= 0 \\ 2\pi r^3 &= 2 \\ r^3 &= \frac{1}{\pi} \\ r &= \frac{1}{\sqrt[3]{\pi}}.\end{aligned}\]

Muodostetaan kulkukaavio:

\(r<\frac{1}{\sqrt[3]{\pi}}\) \(r>\frac{1}{\sqrt[3]{\pi}}\)
\(f'(r)\) \(<0\) \(>0\)
\(f(r)\) väh. kasv.

Koska funktio \(f\) on jatkuva, niin sen pienin arvo saavutetaan kohdassa \(r= \frac{1}{\sqrt[3]{\pi}} \approx 0.683\). Silloin \[h = \frac{1}{\pi r^2} = \frac{1}{\pi \left(\frac{1}{\sqrt[3]{\pi}}\right)^2} = \frac{1}{\frac{\pi}{\pi^{2/3}}} = \frac{1}{\sqrt[3]{\pi}} \approx 0.683.\]

Näin ollen optimaalisen mitan poikkileikkauksen läpimitta on \(2 \cdot 0.683\) dm \( = 1.366\) dm \( \approx 13.7\) cm ja korkeus \(0.683\) dm \( \approx 6.8\) cm.

Funktion \(\pi r^2 + \frac{2}{r}\) kuvaaja.