MS-A0201 - Differentiaali- ja integraalilaskenta 2 (TFM), Luento-opetus, 9.1.2024-19.2.2024
This course space end date is set to 19.02.2024 Search Courses: MS-A0201
Differentiaali- ja integraalilaskenta 2
4. Ääriarvot
Kertausta: ääriarvot yhden muuttujan tapauksessa
Funktiolla f:I⊂R→R on lokaali (paikallinen) maksimi pisteessä a∈I, jos f(x)≤f(a) kaikilla x:n arvoilla jossakin a:n ympäristössä (eli riittävän lähellä pistettä a). Vastaavasti lokaali minimi tarkoittaa sitä, että f(x)≥f(a) jossakin a:n ympäristössä. Maksimi tai minimi on globaali, jos kyseinen epäyhtälö on voimassa kaikilla x∈I.Ääriarvoja voi esiintyä:
- Funktion f kriittisissä pisteissä, joissa f′(x)=0,
- pisteissä joissa f:n derivaatta ei ole määritelty, ja
- määrittelyjoukon I reunalla.
Seuraavaksi yleistetään vastaavat ehdot funktion f:D⊂Rn→R tapaukseen.
Ääriarvot ja usean muuttujan funktiot
Funktiolla f:D⊂Rn→R on pisteessä x0∈D lokaali maksimi, jos jossakin pisteen x0 ympäristössä U⊂D pätee f(x)≤f(x0) kaikilla x∈U. Vastaavasti f:D⊂Rn→R on pisteessä x0∈D lokaali minimi, jos löytyy sellainen pisteen x0 ympäristö U⊂D, että f(x)≥f(x0) kaikilla x∈U. Ääriarvo on globaali eli absoluuttinen, jos kyseinen epäyhtälö on voimassa kaikilla x∈D.Ääriarvoja voi esiintyä:
- Funktion f kriittissä pisteissä eli gradientin nollakohdissa ∇f(x)=0,
- pisteissä joissa ∇f ei ole määritelty, sekä
- määrittelyjoukon D reunalla.
Esimerkki
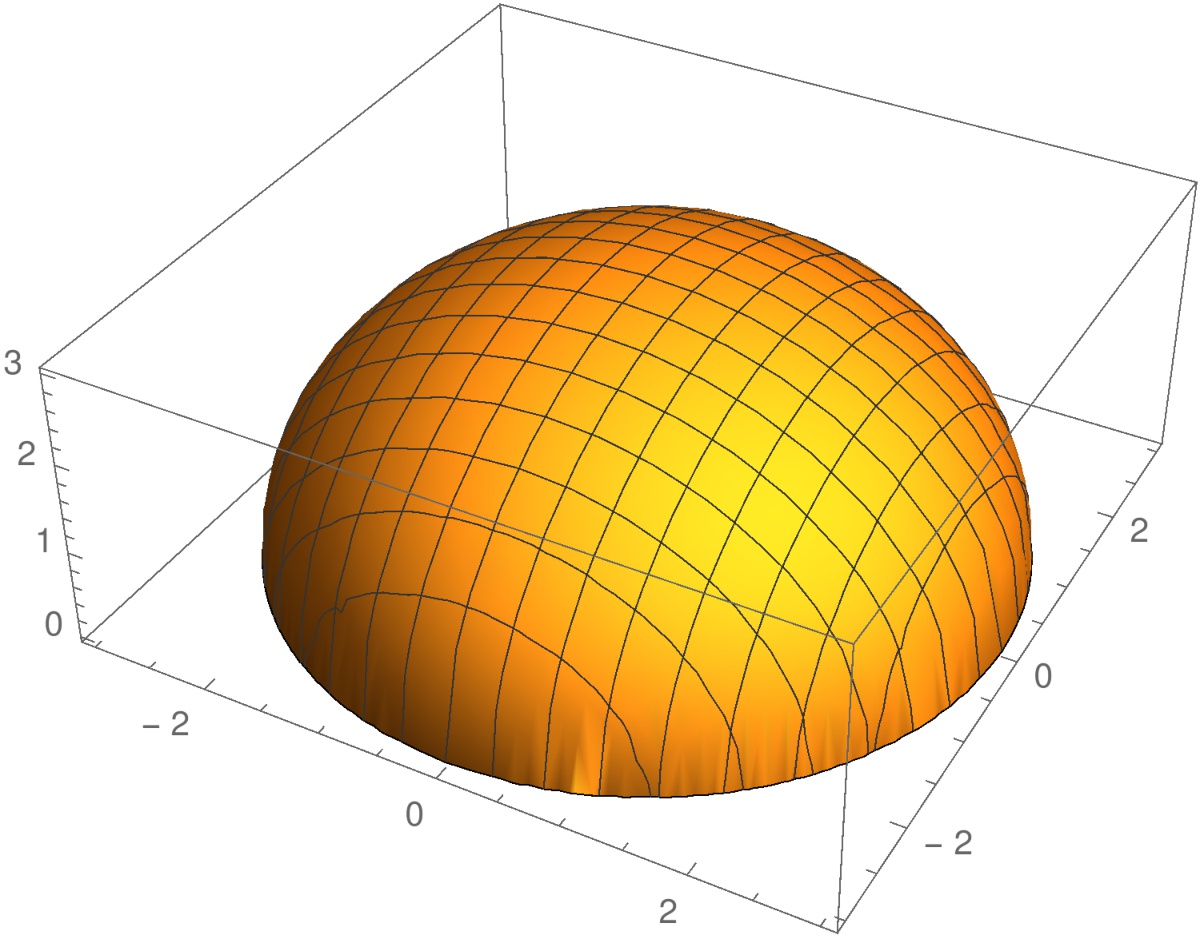
Funktiolla f(x,y)=1−x2−y2 on globaali maksimi f(0,0)=1 pisteessä (0,0). Tämä piste on funktion f kriittinen piste, koska ∇f(0,0)=−2xi−2yj|(0,0)=0.
Esimerkki
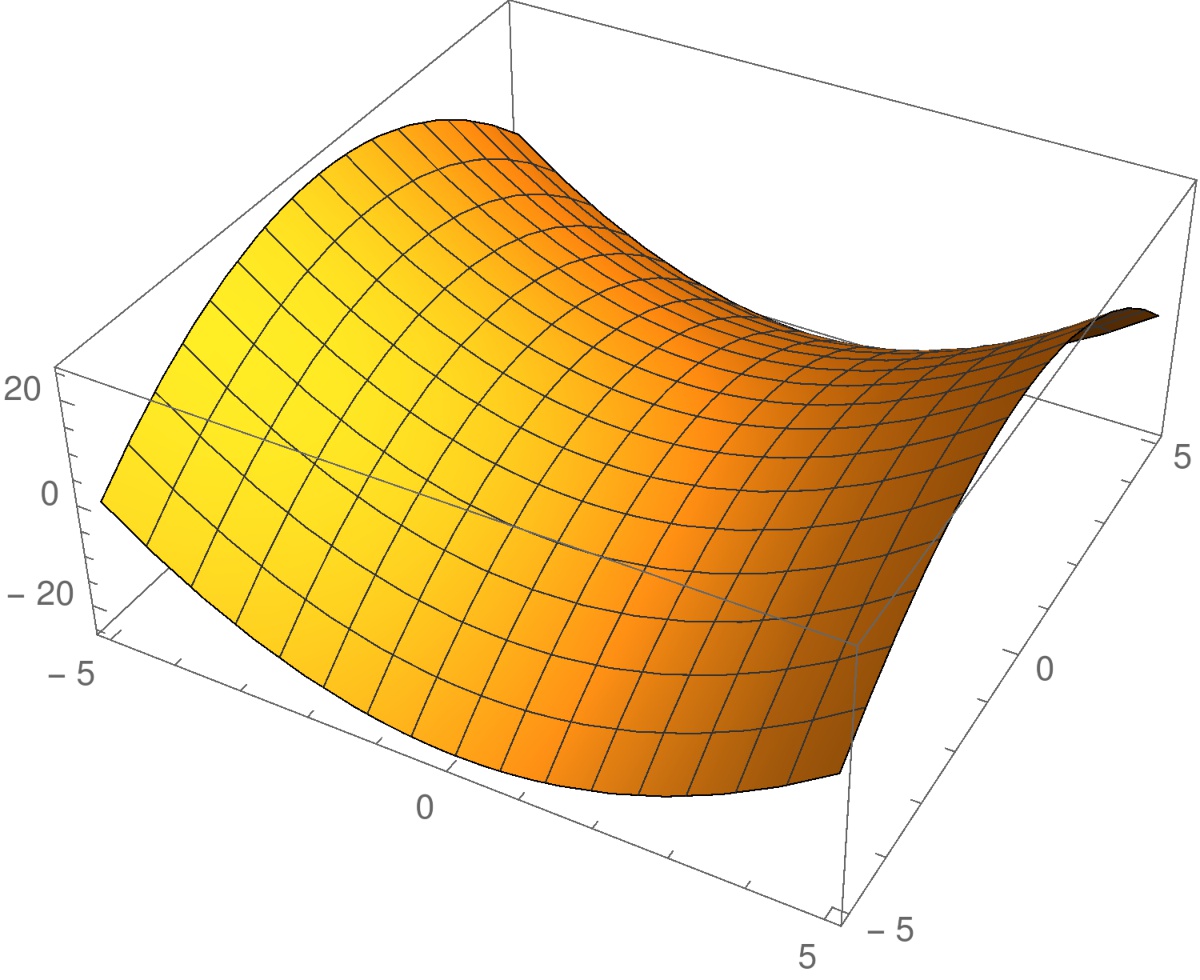
Esimerkki
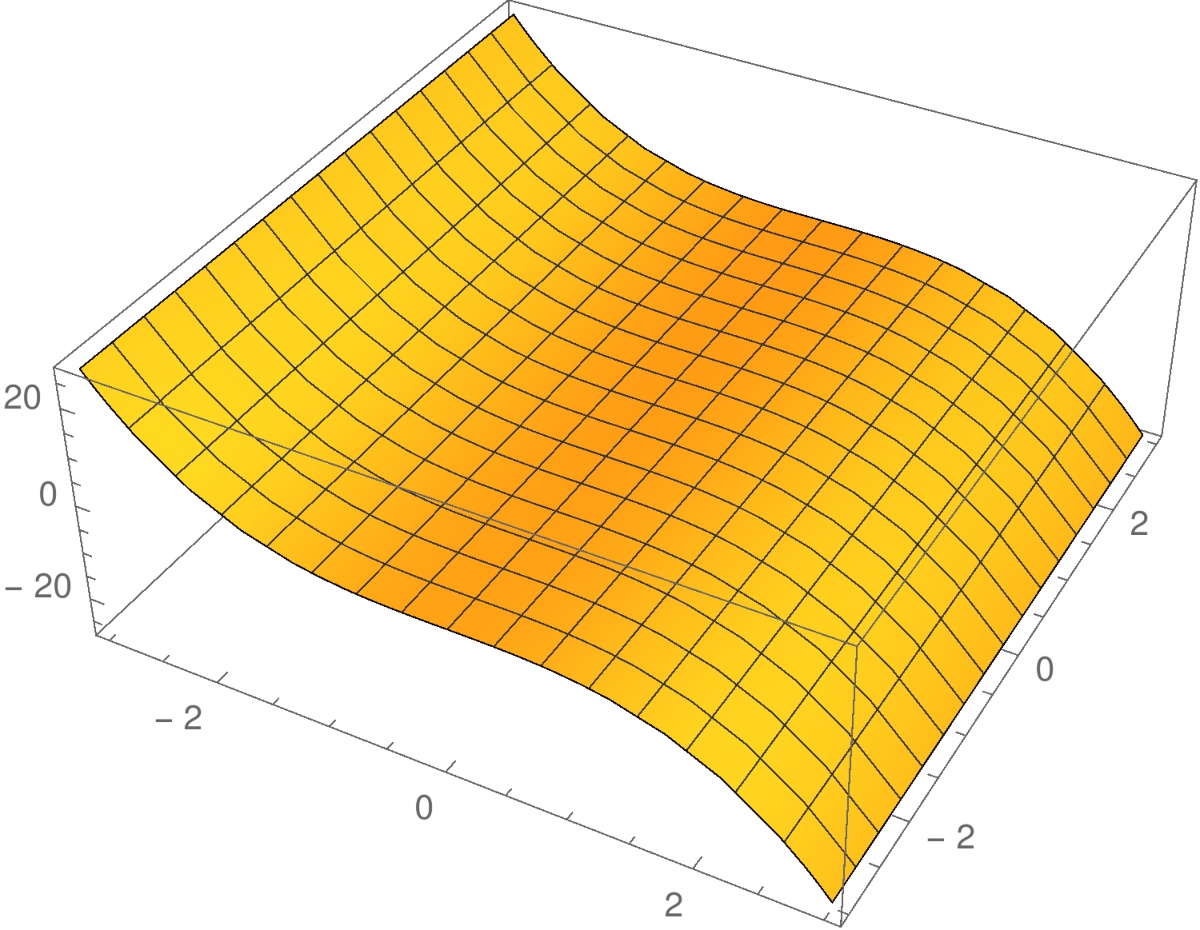
Esimerkki
Esimerkki