MS-A0201 - Differentiaali- ja integraalilaskenta 2 (TFM), Luento-opetus, 9.1.2024-19.2.2024

Regressio-ongelma

Regressioanalyysissa pyritään valitsemaan parametrin $\mathbf{\beta}$ arvo siten, että käyrä $y=f(x;\beta)$ kulkisi mahdollisimman läheltä jokaista havaintopistettä $(x_j,y_j)\in \mathbb{R}^2,\, j=1,2,\ldots ,n.$ Tällaista optimaalisesti valittua käyrää kutsutaan regressiomalliksi $y=f(x;\beta)$, jossa funktion $f$ muoto on valittu tilanteen ja harkinnan mukaan. Kunhan $f$ on valittu, niin eräs ratkaisu käyränsovitusongelmaan on pienimmän neliösumman menetelmä.

Pienimmän neliösumman menetelmä

Pienimmän neliösumman menetelmässä pyritään minimoimaan regressiomallin virhetermien $\varepsilon_j$ $\varepsilon_j = y_j - f(x_j;\beta ) \, , \quad j=1,2,\ldots ,n$ neliösummaa eli funktiota $F(\beta)= \sum_{j=1}^n\varepsilon_j^2 =\sum_{j=1}^n\big(y_j-f(x_j;\beta)\big)^2.$ muuttamalla parametrivektorin $\mathbf{\beta}=(\beta_0,\beta_1,\ldots,\beta_m)$ arvoa. Optimaalinen $\mathbf{\beta}$:n arvo on parametrin $\beta$ pienimmän neliösumman estimaatti eli PNS-estimaatti.

Kysymys: Miksi ei minimoitaisi lauseketta $\sum_{j=1}^n|y_j-f(x_j;\beta)|$ neliösumman sijasta?

PNS-sovitus

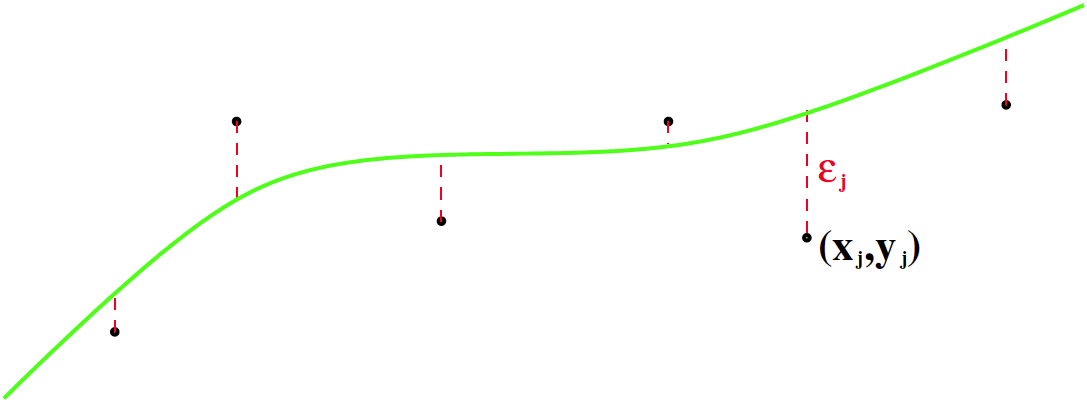
Kuvassa vihreällä parametreista $\mathbf{\beta} = (\beta_1, \beta_2, \ldots , \beta_m)$ riippuva sovitettava funktio $f(x;\mathbf{\beta})$ eräällä kiinteällä parametrin arvolla. Datapisteet $(x_j,y_j)$ ja vastaavat virhetermit $\varepsilon_j$, kun $j = 1, \ldots , n$.

Lineaarinen regressio

Lineaarisessa regressiossa $f(x;\beta) = \beta_0-\beta_1 x$ jossa $\beta = (\beta_0, \beta_1)$ ja neliösumma on $F(\beta_0,\beta_1)=\sum_i (y_i -\beta_0-\beta_1 x_i)^2.$ Etsitään piste $(\beta_0,\beta_1)$ siten, että $\nabla F(\beta_0,\beta_1)=0$.

Lasketaan osittaisderivaatta $\frac{\partial}{\partial \beta_0}F(\beta_0,\beta_1) = 2\big(\beta_1\sum_i x_i+n\beta_0-\sum_i y_i\big).$ Ratkaistaan nollakohta $\beta_0=\frac{1}{n}\sum_i y_i-\frac{\beta_1}{n} \sum_i x_i =\overline{\mathbf{y}} -\beta_1 \overline{\mathbf{x}}$ missä $\overline{\mathbf{x}}$ on datavektorin $\mathbf{x} = (x_1, x_2, \ldots , x_n)$ komponenttien aritmeettinen keskiarvo.

Lasketaan seuraavaksi osittaisderivaatta $\frac{\partial}{\partial \beta_1}F(\beta_0,\beta_1) = 2\big(\beta_0\underbrace{\sum_i x_i}_{=n\overline{x}}+\beta_1\sum_i x_i^2-\sum_i x_iy_i\big).$ Sijoittamalla $\beta_0$:n lauseke, saadaan $n\overline{\mathbf{x}} \overline{\mathbf{y}} - n \beta_1 \overline{\mathbf{x}} ^2+\beta_1 \sum_i x_i^2-\sum_i x_i y_i=0.$ Ratkaistaan nollakohta: $\beta_1=\frac{n\overline{\mathbf{x}} \overline{\mathbf{y}} -\sum_i x_iy_i}{n\overline{\mathbf{x}} ^2-\sum_i x_i^2} = \frac{\sum_i(x_i-\overline{\mathbf{x}})(y_i-\overline{\mathbf{y}})}{\sum_i(x_i-\overline{\mathbf{x}})^2}.$ Tarkista jälkimmäinen yhtälö!

Esimerkki

Sovita PNS-suora dataan

ja estimoi (ekstrapoloi) $y$ kun $x=5$.

Saadaan $\overline{\mathbf{x}}=2.0$, $\overline{\mathbf{y}}= 1.842$, ja $\beta_1 = \frac{-1.13}{10.0} = -0.113.$ Siten $\beta_0=1.842 +0.113\cdot 2.0= 2.068$. Näin ollen $y=-0.113x + 2.068$, ja kysytty estimaatti pisteessä $x=5$ on $y=-0.113\cdot 5 + 2.068=1.503$.

Esimerkki: Toisen asteen sovitus

Tutkitaan lisäaineen määrän $x$ vaikutusta kuivumisaikaan $y$. Eri lisäaineen määrillä $x_i$ (grammaa) saatiin kuivumisajat $y_i$ (tuntia), $i=1,\ldots,9$:

Huomataan, että kuivumisajan riippuvuus lisäaineen määrästä on epälineaarista.

Minimikohdan estimoimiseksi sovitetaan havaintoihin paraabeli $y=\beta_0+\beta_1x+\beta_2x^2.$

Pienimmän neliösumman yhtälöryhmä mallille on $\frac{\partial}{\partial \beta_k} \sum(y_i-\beta_0-\beta_1x_i-\beta_2x_i^2)^2 = 0, \qquad k=0,1,2.$ Näistä saadaan yhtälöryhmä $\left\{ \begin{array}{rcl} n\beta_0 + \beta_1\sum x_i +\beta_2 \sum x_i^2 &=& \sum y_i,\\ \beta_0\sum x_i+\beta_1 \sum x_i^2+\beta_2 \sum x_i^3 &=& \sum x_iy_i\\ \beta_0\sum x_i^2+\beta_1 \sum x_i^3+\beta_2 \sum x_i^4 &=& \sum x_i^2y_i. \end{array}\right.$ Laskemalla yhtälöryhmän kertoimet havainnoista saadaan $\left\{ \begin{array}{rcl} 9\beta_0 + 36\beta_1 + 204\beta_2 &=& 72.1\\ 36\beta_0 +204\beta_1 + 1296 \beta_2 &=& 266.6 \\ 204 \beta_0 +1296\beta_1 + 8772\beta_2 &=& 1515.4 \end{array}\right.$

Ratkaisuna ovat $\beta_0=11.15$, $\beta_1=-1.806$ ja $\beta_2=0.1803$. Pienimmän neliösumman mielessä parhaiten havaintoihin liittyvä paraabeli on siten $y=11.15 - 1.806x + 0.1803 x^2.$