7. Taso- ja avaruusintegraalit

7.5. Muuttujanvaihto tasointegraalissa

Napakoordinaatit

Piste (x,y)\in \mathbb{R}^2 voidaan kirjoittaa muodossa (r,\theta), missä r\geq0 ja 0\le \theta < 2\pi. Napakulma \theta on yksikäsitteinen jos r > 0.

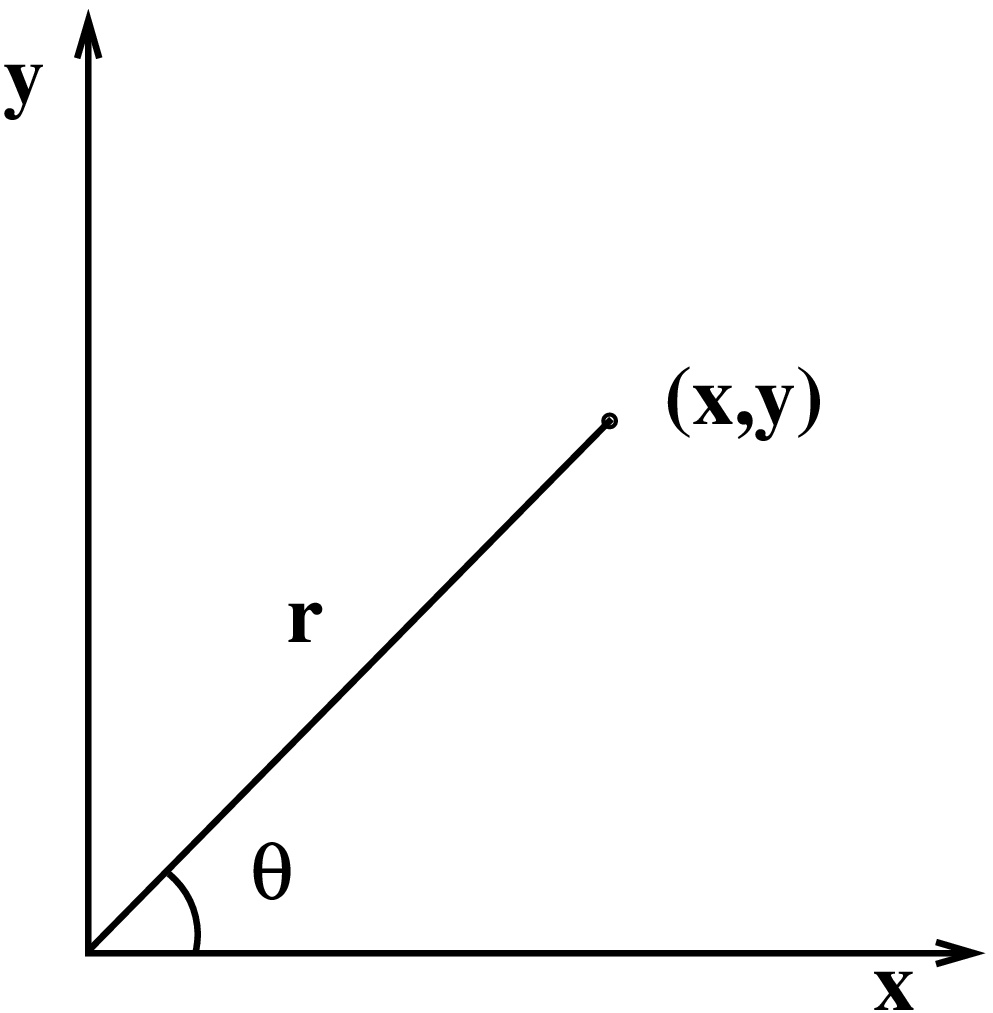
napakoordinaatisto

Alkeisgeometriasta saadaan kaavat \left\{ \begin{array}{l} x=r\cos \theta\\ y=r\sin \theta \end{array}\right. \Leftrightarrow \left\{ \begin{array}{l} r^2=x^2+y^2 \\ \tan{\theta} = y/x. \end{array}\right. Vrt. kompleksiluvun polaarimuoto x + i y = r e^{i \theta}.

Koordinaatistomuunnoksen (r, \theta) \mapsto (x,y) Jacobin determinantille saadaan kaava \frac{\partial(x,y)}{\partial (r,\theta)} = \left|\begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array}\right| = \left|\begin{array}{cc} \cos \theta & -r\sin \theta\\ \sin \theta & r\cos\theta \end{array}\right| = r. Siten muuttujanvaihtokaavaa varten saadaan pinta-alan venytys dx\,dy = \bigg|\frac{\partial(x,y)}{\partial (r,\theta)}\bigg| \,dr\,d\theta = r\,dr\,d\theta. Tasointegraali napakoordinaateissa \iint_D f(x,y)\,dx\,dy = \iint_G g(r,\theta)r\,dr\,d\theta, missä g(r,\theta) = f(r\cos\theta,r\sin\theta).

Esimerkki

(i) Olkoon D=\lbrace (x,y)\in \mathbb{R}^2 : 1 < x^2 + y^2 < 4\rbrace. Lasketaan napakoordinaateissa integraali I=\iint_D \frac{1}{x^2+y^2}\,dx\,dy. Saadaan I=\int_0^{2\pi}\int_1^2\frac{1}{r^2}r\,dr\,d\theta = \int_0^{2\pi} d\theta \cdot \int_1^2\frac{dr}{r} =2\pi\ln r\Big|_{r=1}^2 = 2\pi \ln 2.

(ii) Integraali \int_{-\infty}^\infty e^{-x^2}\,dx on erittäin tärkeä mm. todennäköisyyslaskennassa ja tilastotieteessä. Tämä integraali on vaikea, koska integraalifunktiota ei ole mahdollista kirjoittaa alkeisfunktioiden avulla.

Integraali on kuitenkin mahdollista laskea seuraavan tempun avulla: Huomataan aluksi, että I = \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-x^2-y^2}\,dx\,dy = \bigg(\int_{-\infty}^\infty e^{-x^2}\,dx\bigg)^2. Laskemalla epäoleellinen tasointegraali napakoordinaateissa I = \int_0^{2\pi}\int_0^\infty e^{-r^2}r\,dr\,d\theta = \int_0^{2\pi}d\theta \cdot \int_0^\infty r e^{-r^2}\,dr = 2\pi \int_0^\infty{r e^{-r^2}\,dr} = -\pi \lim_{R \to \infty}{\int_0^R (-2r) e^{-r^2}\,dr}.

Nyt \frac{d}{dr} e^{-r^2} = -2r e^{-r^2}, joten integraaliksi saadaan: \int_0^R (-2r) e^{-r^2}\,dr = e^{-R^2} - 1 Viemällä R \to \infty tulee I = \pi ja siitä alkuperäisen integraalin arvo \int_{-\infty}^\infty e^{-x^2}\,dx = \sqrt{I} = \sqrt{\pi}. Miksi temppu toimi?