MS-A0201 - Differentiaali- ja integraalilaskenta 2 (TFM), Luento-opetus, 9.1.2024-19.2.2024

Muuttujanvaihto avaruusintegraalissa

Muunnoskaavat $(u,v,w) \mapsto (x,y,z)$ ovat $\left\{ \begin{array}{l} x=x(u,v,w),\\ y=y(u,v,w),\\ z=z(u,v,w). \end{array}\right.$ Tällöin $dx\,dy\,dz = \bigg|\frac{\partial(x,y,z)}{\partial (u,v,w)}\bigg|\,du\,dv\,dw,$ missä $\frac{\partial(x,y,z)}{\partial (u,v,w)} = \left|\begin{array}{ccc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w} \end{array}\right|.$ Jos siis $g(u,v,w) = f(x(u,v,w),y(u,v,w),z(u,v,w))$, niin $\iiint_D f(x,y,z)\,dx\,dy\,dz = \iiint_G g(u,v,w)\, \bigg|\frac{\partial(x,y,z)}{\partial (u,v,w)}\bigg|\,du\,dv\,dw.$

Sylinterikoordinaatit

Koordinaatit $(r,\theta,z)$, missä $r \geq 0$, $0\le \theta$, $z\in\mathbb{R}$. Suoralla $r = 0$ (eli $z$-akselilla) napakulma $\theta$ ei ole yksikäsitteinen.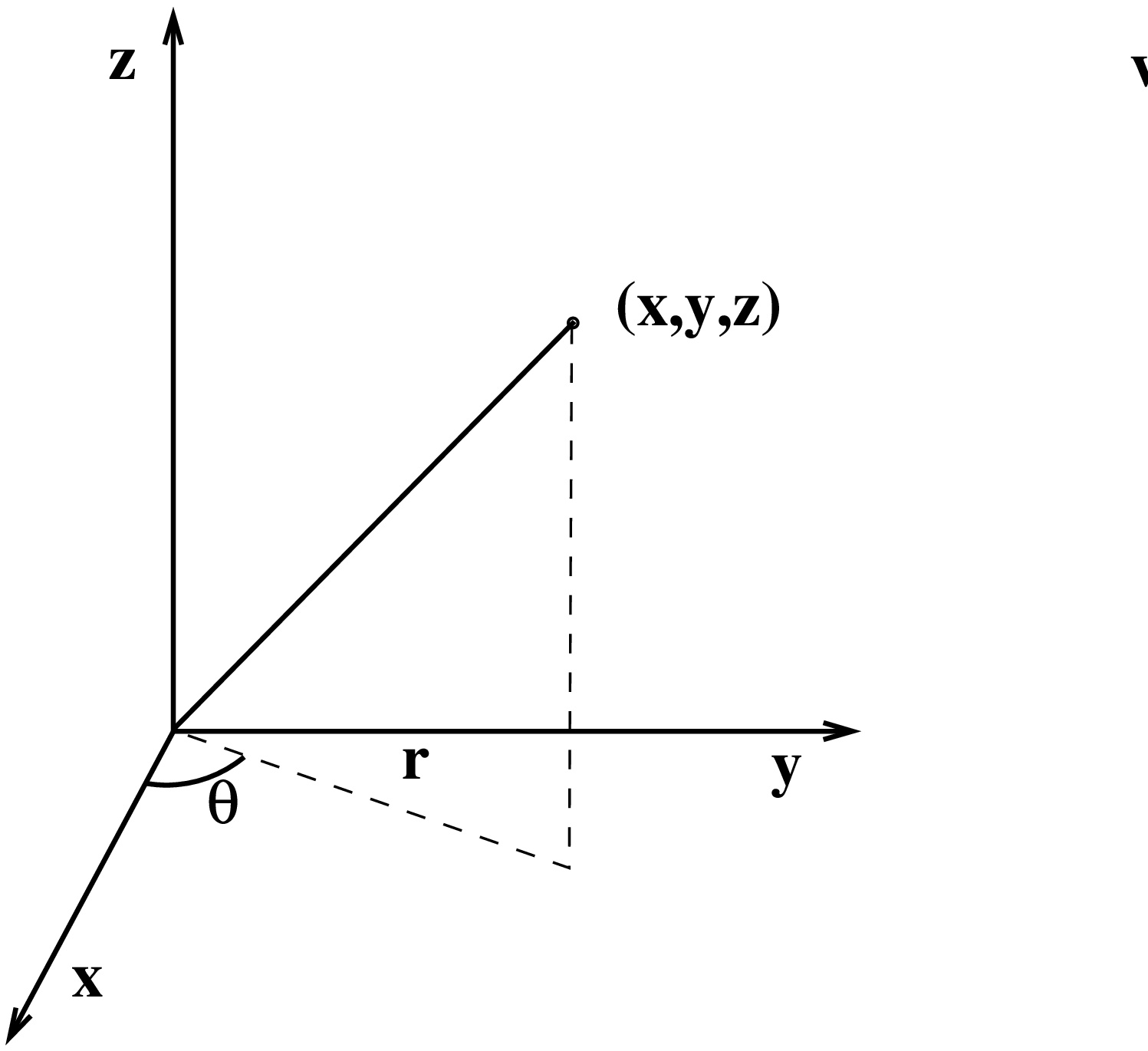

Tällöin muunnoskaavat $(r,\theta,z) \mapsto (x,y,z)$ ovat $$\begin{align*} \begin{cases} x &= r\cos\theta, \\ y &= r\sin\theta, \\ z &= z. \end{cases} \end{align*}$$ Ja muunnoksen Jacobin determinantiksi saadaan $dx\,dy\,dz = \bigg|\frac{\partial(x,y,z)}{\partial (r,\theta,z)}\bigg|\,dr\,d\theta\,dz = r\,dr\,d\theta\,dz.$

Sylinterikoordinaateissa on helppo esittää pyörähdyskappaleita $z$-akselin ympäri muodossa $r = f(z), \quad \text{jossa} \quad z \in [a,b] \text{ ja } \theta \in [0, 2 \pi),$ missä $f$ on ei-negatiivinen funktio. Sylinterisymmetriset tehtävät!

Esimerkki

Lasketaan funktion $f$ määräämän pyörähdyskappaleen $\Omega$ tilavuus $\iiint_{\Omega} dx\, dy\, dz = \int_a^b\int_0^{2\pi}\int_0^{f(z)} r\,dr\,d\theta\,dz$ $= \int_a^b \left (2\pi \cdot \frac{1}{2}f(z)^2 \right ) \, dz = \pi \int_a^b f(z)^2 \, dz,$ mikä lienee tuttu kaava.

Pallokoordinaatit

Koordinaatit $(r,\theta,\phi)$, missä $r \geq 0$, $0\le \theta$, $0\le \phi \leq \pi$.

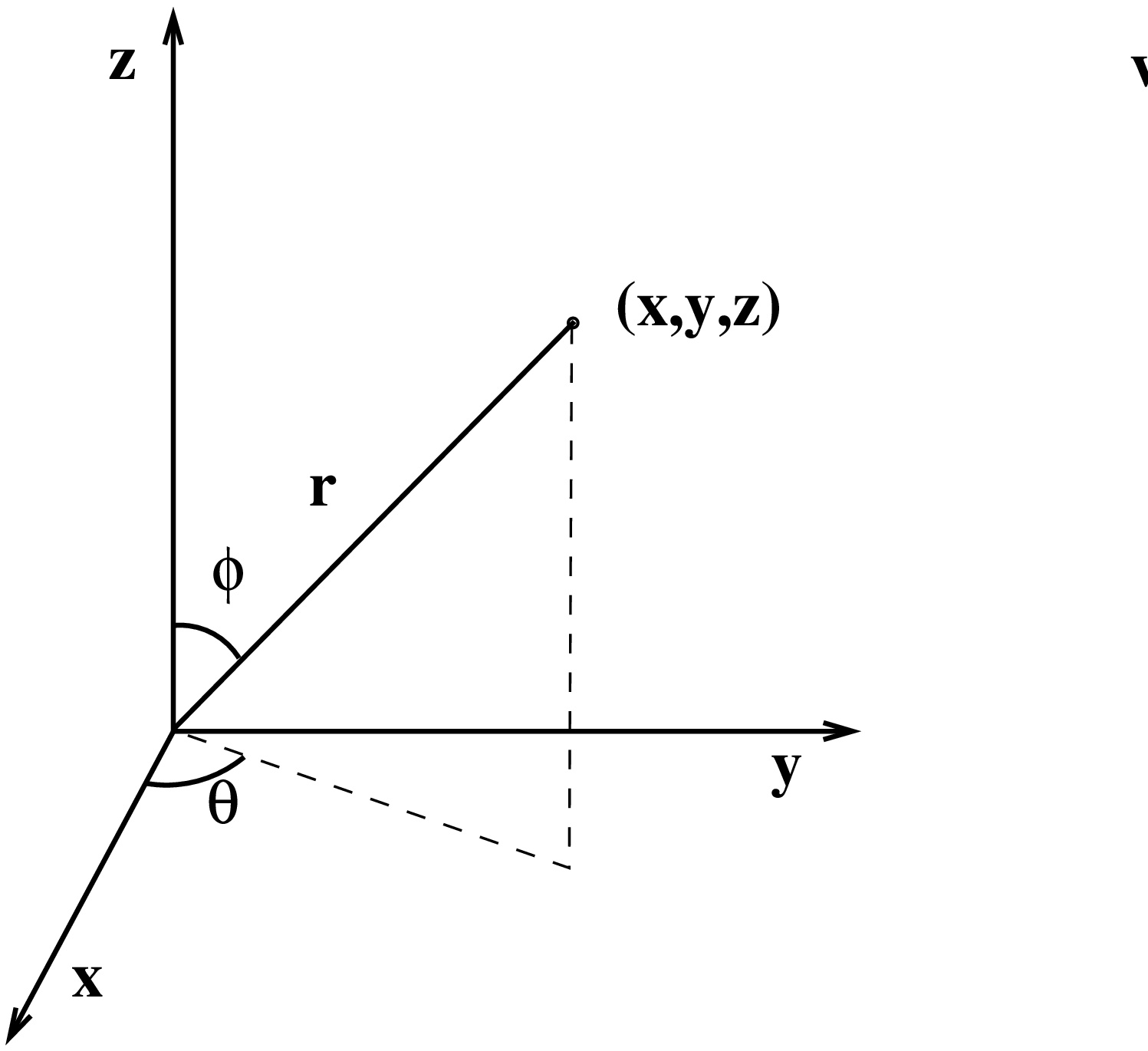
Korotus- eli napakulmaa $\pi/2 - \phi$ käytetään usein $\phi$:n sijasta. Atsimuuttikulma $\theta$ ja korotuskulma ovat yksikäsitteisiä, jos pisteen etäisyys $z$-akselista $> 0$. Muunnoskaavat ovat $$\begin{align*} \begin{cases} x&=r\sin\phi \cos\theta,\\ y&=r\sin\phi \sin\theta,\\ z&=r\cos\phi, \end{cases} \end{align*}$$ ja muunnoksen Jacobin determinantiksi saadaan $dx\,dy\,dz = \bigg|\frac{\partial(x,y,z)}{\partial (r,\theta,\phi)}\bigg|\,dr\,d\theta\,d\phi = r^2\sin\phi \,dr\,d\theta\,d\phi.$

Esimerkki

Lasketaan $R$-säteisen pallon $\mathbb{B}^3(R)$ tilavuus: $V(\mathbb{B}^3) = \iiint_{\mathbb{B}^3(R)} 1\,dx\,dy\,dz = \int_0^R\int_0^{2\pi}\int_0^\pi r^2\sin\phi\,d\phi\,d\theta\,dr$ $= \int_0^R\int_0^{2\pi} -r^2\cos\phi\bigg|_{\phi=0}^\pi\,d\theta\,dr = \int_0^R\int_0^{2\pi} 2r^2\,d\theta\,dr$ $=\int_0^R 4\pi r^2\,dr = \frac{4\pi r^3}{3}\bigg|_{r=0}^R = \frac{4\pi R^3}{3}.$