Previous
Next

6. Electrochemical reaction kinetics

6.1. Reaction rate via the free energy model

Let us consider a redox reaction

\( \displaystyle\text{O}+n\text{e}^- \)\(\ce{ <=> }\)\( \text{R} \) (6.1)

where n electrons are transferred to the oxidized species ’O’, forming the reduced species ’R’. At equilibrium, the following equation applies:

\(\displaystyle \mu_{\text{R}}^0+RT\text{ln}a_{\text{R}}+z_{\text{R}}F \phi^w= \mu_{\text{O}}^0+RT\text{ln}a_{\text{O}}+z_{\text{O}}F \phi^w+n(\mu_{\text{e}}^0+RT\text{ln}a_{\text{e}}-F \phi^{\text{M}}) \) (6.2)

where \( \phi^w \) is the Galvani potential in the aqueous phase and \( \phi^{\text{M}} \) that of an electron (in the electrode); the other variables are defined in Chapter 2. The activity of an electron in the solid electrode (most commonly a metal) ae = 1, and n = zO - zR. Hence, rearranging Equation (6.2), the Nernst equation is obtained:

\( \displaystyle\phi^{\text{M}}-\phi^{\text{w}}=\Delta\phi_{eq}=-\frac{\Delta G^0}{nF}+\frac{RT}{nF}\text{ln} \left(\frac{a_{\text{O}}}{a_{\text{R}}}\right)_{eq}=\Delta\phi^0+\frac{RT}{nF}\text{ln}\left(\frac{a_{\text{O}}}{a_{\text{R}}}\right)_{eq} \) (6.3)

where

\( \displaystyle\Delta G^0=\mu_{\text{R}}^0-\mu_{\text{O}}^0-n\mu_{\text{e}}^0 \) (6.4)

When the electrode potential \( \phi^{\text{M}} \) is changed, it follows that

\( \displaystyle nF(\Delta\phi-\Delta\phi_{eq})=(RT\text{ln}a_{\text{O}}-RT\text{ln}a_{\text{O}, eq})-(RT\text{ln}a_{\text{R}}-RT\text{ln}a_{\text{R}, eq})=\Delta\mu_{\text{O}}-\Delta\mu_{\text{R}} \) (6.5)

In other words, the change in the electrode potential is converted to a change in the chemical potentials of the species residing in the solution phase.

The Nernst equation contains the activities of the species involved in the reaction, but the estimation of their activity coefficients is not always easy. Fortunately, the ratio of the activity coefficients approaches unity much faster than the individual coefficients. The Nernst equation is therefore most often written in terms of concentrations:

\( \displaystyle E=E^0+\frac{RT}{nF}\text{ln}\left(\frac{\gamma _{\text{O}}}{\gamma _{\text{R}}}\right)_{eq}+\frac{RT}{nF}\text{ln}\left(\frac{c_{\text{O}}}{c_{\text{R}}}\right)_{eq}=E^{0'}+\frac{RT}{nF}\text{ln}\left(\frac{c_{\text{O}}}{c_{\text{R}}}\right)_{eq} \) (6.6)

In Equation (6.6) the Galvani potential \( \phi \) is replaced by E to emphasize that the electrode potential is measured against some reference value. The quantity E0’ is known as the formal potential. The use of formal potential is also practical because during an electrochemical reaction the concentrations of O and R on the electrode surface change as a function of the electric current, and the formal potential provides one of the boundary conditions of the transport problem. We will look at this in more detain in Chapter 6.2.

The rate of reaction (6.1), r, can be written in the usual form as

\( \displaystyle r=k_{red}c_{\text{O}}^s-k_{ox}c_{\text{R}}^s \) (6.7)

where kred and kox are the rate constants (cm s-1) of the heterogeneous reduction and oxidation reactions respectively and the superscript ’s’ denotes the surface concentrations. Let’s assume that the rate constants follow the Arrhenius formalism:

\( \displaystyle k_x=A_xe^{-\Delta G_{x,a}^{\ddagger}/RT} \)     \( x=red, ox \)
 (6.8)

In Equation (6.8) Ax is the pre-exponential (frequency) factor of reaction x and \( \Delta G_{x,a}^{\ddagger} \)its activation energy. At equilibrium r = 0, viz \( k_{red}c_{\text{O}}^s=k_{ox}c_{\text{R}}^s \), and when E = E0’*, \( c_{\text{O}}^s=c_{\text{R}}^s \). This means that kred = kox and we call this quantity as the standard rate constant k0:

\( \displaystyle k^0=k_{red}(E=E^{0'})=k_{ox}(E=E^{0'}) \) (6.9)

Figure 6.1 shows a scheme of the free energy profiles at equilibrium (left) and after changing the electrode potential (right); the activation energies or the pre-exponential factors do not need to be equal in both oxidation and reduction reactions, although they are shown this way for the sake of clarity.

When the electrode potential is changed, it can be interpreted as the change of the chemical potential or free energy of either of the species, as previously shown. On the right of Figure 6.1 the electrode potential is raised by \( \Delta E \), raising the free energy of R by \( \Delta G=nF\Delta E \), consequently shifting the reaction equilibrium towards oxidation. The energy barrier of the oxidation reaction does not, however, reduce by \( nF\Delta E \) but, as can be seen in the plot, by the fraction that is denoted \( \alpha nf\Delta E \).† Accordingly, the energy barrier of the reduction reaction is increased by the fraction \( (1- \alpha)nf\Delta E \). The quantity a is known as the charge transfer coefficient. Its value depends on the symmetry of the energy barrier and the electrode potential, taking the value 0.5 in the vicinity of E0’, regardless of the symmetry.

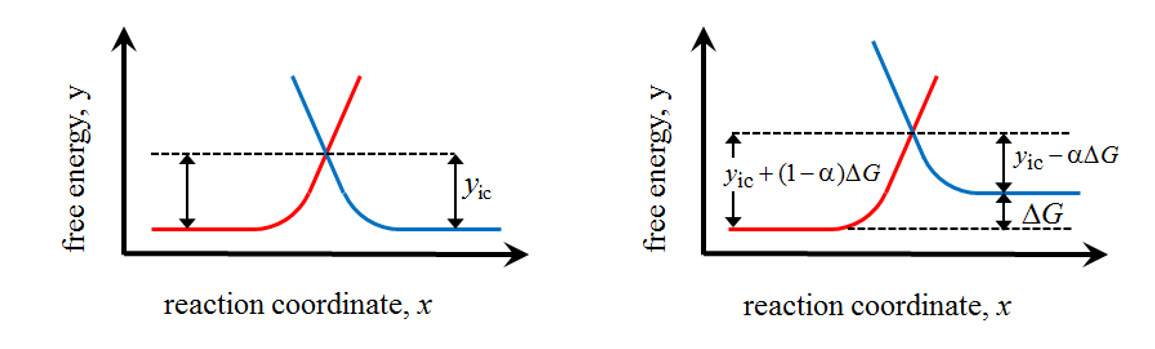
Free energy profiles at equilbrium (left) and after changing the electrode potential (right).

Figure 6.1. Free energy profiles at equilbrium (left) and after changing the electrode potential (right).

The rate constants are according to the Arrhenius formalism


\( \displaystyle k_{red}=k^0e^{(\alpha-1)nf(E-E^{0'})} \) and \( k_{ox}=k^0e^{\alpha nf(E-E^{0'})} \)

 (6.10)

where f = F/RT. Equations (6.10) are general in the sense that in all approaches the form of the rate constants remains the same, only the the interpretation of the activation energy and the charge transfer coefficient depend on the model applied.‡

Inserting the rate constants from (6.10) into Equation (6.7) at equilibrium (\( r \equiv0 \)), the Nernst equation is restored, i.e. our kinetic model agrees with thermodynamics:

\( \displaystyle\frac{c_{\text{O}}^s}{c_{\text{R}}^s}=\frac{k_{ox}}{k_{red}}=e^{nf(E-E^{0'})} \) (6.11)


*Since the potential of a single electrode \( \Delta\phi \) cannot be measured, \( E=\Delta\phi+K \) where K is a constant fixing of the potential scale. We therefore use an arbitrary ’E scale’ to emphasize that our treatise is independent of the reference potential, provided that E0’ is defined on the same scale.

† This notation follows the convention used in the following books: K.J. Vetter, Electrochemical kinetics, Academic Press, New York 1967; T, Erdey-Grúz, Kinetics of electrode processes, Adam Hilger, Lontoo 1972.

‡ In the analysis of multistep reaction mechanisms, n denotes the number of electrons transferred in the rate-determining step, often denoted by na, that is nearly always one. In equation (6.12), however, n denotes the total number of electrons transferred in a redox reaction. Obviously, na ≤ n. These issues are relevant in, e.g. oxygen evolution.


Previous
Next