Previous
Next

5. Electrical double layer and adsorption

5.2. Electrocapillary equation

Electric charges affect the surface tension of the interface of two phases. If one of these phases is a metal and another is an electrolyte solution, the phenomenon is called electrocapillarity.

The surface tension of an ideally polarizable electrode (see Chapter 1.3.4) always depends on the potential. To understand the dependency of surface tension, composition, and cell potential, consider a situation where one of the electrodes is ideally nonpolarizable. The potential of this reference electrode is therefore constant, and the change in the cell potential has an effect on the interface of the working electrode and the electrolyte. The working electrode must be ideally nonpolarisable.

Let us look at a cell, in which a hydrogen electrode is the ideally nonpolarizable reference electrode and a mercury electrode is the ideally polarizable working electrode. The electrolyte in the cell is an aqueous solution of hydrogen chloride.

Pt(s) | H2(g) | HCl(aq) | Hg(l) | Pt(s)    (5.17)

As we showed in Chapter 2, the chemical potentials can be replaced by the electrochemical potentials of ions. In the bulk of the solution, the electroneutrality condition cancels the potential terms out, but there is an excess of charge at the interface, in other words a local deviation from the electroneutrality condition. Applying the Gibbs adsorption isotherm (5.12) to the interface of HCl-Hg using the relative surface excesses with respect to water (5.16), we obtain

\( \displaystyle -d\gamma=\left(\Gamma_{\text{Hg}^+}^{\sigma}d\tilde\mu_{\text{Hg}^+}+\Gamma_{\text{e}^-}^{\sigma}d\tilde\mu_{\text{e}^-}^{\text{Hg}}\right)+\left(\Gamma_{\text{H}^+}^{\sigma}d\tilde\mu_{\text{H}^+}+\Gamma_{\text{Cl}^-}^{\sigma}d\tilde\mu_{\text{Cl}^-}\right) \) (5.18)

There is an equilibrium between the metal ions and electrons in mercury and between the ions and molecules in the electrolyte. Thus

\( \displaystyle\mu_{\text{Hg}}=\tilde\mu_{\text{Hg}}=\tilde\mu_{\text{Hg}^+}+\tilde\mu_{\text{e}^-}^{\text{Hg}} \)
 (5.19)
\( \displaystyle\mu_{\text{HCl}}=\tilde\mu_{\text{HCl}}=\tilde\mu_{\text{H}^+}^{\text{HCl}}+\tilde\mu_{Cl^-} \)
  (5.20)

The excess of charges at the interface of metallic mercury and the electrolyte, \( \sigma \)m and \( \sigma \)s can be expressed as

\( \displaystyle\sigma^m=\sum\limits_iz_iF\Gamma_i^{\sigma}=F\left(\Gamma_{\text{Hg}^+}^{\sigma}-\Gamma_{\text{e}^-}^{\sigma}\right) \)

 (5.21)
\( \displaystyle\sigma^s=-\sigma^m=F\left(\Gamma_{\text{H}^+}^{\sigma}-\Gamma_{\text{Cl}^-}^{\sigma}\right) \) (5.22)

Substituting Equations (5.19)-(5-22) into Equation (5.18) we obtain

\( \displaystyle -d\gamma=\Gamma_{\text{Hg}^+}^{\sigma}d\mu_{\text{Hg}}+\Gamma_{\text{Cl}^-}^{\sigma}d\mu_{\text{HCl}}-\frac{\sigma^m}{F}\left(d\tilde\mu_{\text{H}^+}^{\text{HCl}}+d\tilde\mu_{\text{e}^-}^{\text{Hg}}\right) \) (5.23)

Based on the equilibrium conditions at the phase boundaries, we can write

\(\displaystyle \tilde\mu_{\text{e}^-}^{\text{Hg}}=\tilde\mu_{\text{e}^-}^{\text{Pt,w}} \)

 (5.24)
\( \displaystyle\tilde\mu_{\text{e}^-}^{\text{H}_2}=\tilde\mu_{\text{e}^-}^{\text{Pt,r}} \)

 (5.25)
\( \displaystyle\tilde\mu_{\text{H}^+}^{\text{H}_2}=\tilde\mu_{\text{H}^+}^{\text{HCl}} \)
 (5.26)


where superscript w denotes the working electrode and r the reference electrode. On the other hand, the composition of gas in the hydrogen phase of the reference electrode is constant and because of the equilibrium H2  \(\ce{ <=> }\)  2 H+  +  2 e– we have

\( \displaystyle\tilde\mu_{\text{H}^+}^{\text{H}_2}=-\tilde\mu_{\text{e}^-}^{\text{H}_2} \) (5.27)

Applying the definition of potential E

\( dG=-nFdE \) (5.28)

The last term of Equation (5.23) can be written as

\( -\displaystyle\frac{\sigma^m}{F}(d\tilde\mu_{\text{e}^-}^{\text{Pt,w}}+\tilde\mu_{\text{e}^-}^{\text{Pt,r}})=\sigma^mdE \) (5.29)

Thus,

\( \displaystyle -d\gamma=\Gamma_{\text{Hg}^+}^{\sigma}d\mu_{\text{Hg}}+\Gamma_{\text{Cl}^-}^{\sigma}d\mu_{\text{HCl}}+\sigma^mdE \) (5.30)

This is called the electrocapillary equation. The name is of historic origin, derived from the early application of the equation to the determination of surface tension at mercury-electrolyte interfaces. The equation implies that varying the concentration and following the change in the surface tension at constant potential, the surface concentrations of ions can be determined. On the other hand, if the change in potential is followed when the composition of the solution is constant, the surface charge \( \sigma \)m can be found.

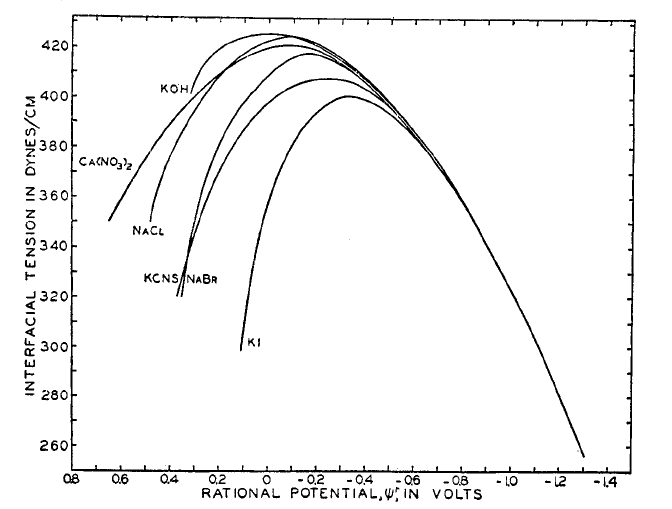
 Electrocapillary curves

Figure 5.3. Electrocapillary curves, i.e. surface tension of mercury electrode as a function of potential in various electrolytes. The potential is plotted with respect to the potential of zero charge for NaF. D.C. Grahame, Chem. Rev. 41 (1947) 441.

Figure 5.3 shows the nearly parabolic shape typical of electrocapillary curves which describe the surface tension as a function of potential for electrolyte solutions in contact with the mercury electrode. If the mercury is pure, \( \mu \)Hg = 0 and d\( \mu \)Hg = 0. Also, d\( \mu \)HCl = 0, if the concentration of the acid is assumed to be constant. In this case, the previous equation becomes 

\( \displaystyle\left(\frac{d\gamma}{dE}\right)_{P,T,\mu_{\text{HCl}}}=-\sigma^m \) (5.31)

It is evident that the slope of the tangent to the electrocapillary curve gives the magnitude of the excess charge at any potential.

 

Even though the curves for each solution are substantially different from each other, we can observe a common feature in all curves: the existence of a maximum surface tension. The corresponding potential is the potential of zero charge (PZC), where \( \sigma \)m = \( \sigma \)s = 0. At more negative potentials, the surface of the electrode has a negative excess charge, and at more positive potentials the surface charge is positive. The charge at the surface weakens surface tension because like charges tend to repel each other.

Neutral organic molecules are typically best adsorbed close to the potential of zero charge because at PZC the polar water molecules in the inner Helmhotz plane are less organized and neutral molecules can more easily penetrate the inner parts of the double layer. The surface coverage varies as a function of potential. The surface coverage \( \theta \) is the fraction of the electrode surface that is covered by molecules (0 < \( \theta \) < 1). If the molecules are specifically adsorbed, the previous model is not valid and the surface coverage can be independent of the potential.

The capacitance of the double layer per unit area C is the derivative of the excess charge with respect to the potential at constant composition

\( \displaystyle C_{dl}=\left(\frac{\partial\sigma^m}{\partial E}\right)_{\mu,T} \) (5.32)



Previous
Next