MS-A0103 - Differentiaali- ja integraalilaskenta 1 (ELEC1, ENG1), Luento-opetus, 4.9.2023-18.10.2023
This course space end date is set to 18.10.2023 Search Courses: MS-A0103
VERKKOKIRJA
Differentiaali- ja integraalilaskenta - verkkokirja, tekijä Pekka Alestalo
Englanninkielisen MOOC-kurssin luentomateriaali, joka perustuu tämän kurssin luentoihin. Mukana on interaktiivisia JSXGraph-kuvia, joita ei ole suomenkielisissä luentokalvoissa. Toistaiseksi vain luvut 1-5, 7 ja 9 ovat suomeksi.
1. Jonot
Sisältö
- Peruskäsitteet
- Tärkeitä jonoja
- Suppeneminen ja raja-arvo
Jonot
Tämä luku sisältää tärkeimmät jonoihin liittyvät käsitteet. Käsittelemme käytännössä vain reaalilukujonohin liittyviä asioita.
Huom. Koska  on järjestetty joukko, niin myös jonon termeillä
on järjestetty joukko, niin myös jonon termeillä  on vastaava järjestys. Sen sijaan joukon alkioilla ei yleisessä tapauksessa
ole määrättyä järjestystä.
on vastaava järjestys. Sen sijaan joukon alkioilla ei yleisessä tapauksessa
ole määrättyä järjestystä.
Määritelmä: Jonon termit ja indeksit
Jonoille voidaan käyttää myös merkintöjä
Funktion  perusteella jokaiseen jonon termiin liittyy yksikäsitteinen lukua
perusteella jokaiseen jonon termiin liittyy yksikäsitteinen lukua  to each term. Se merkitään alaindeksinä ja sitä kutsutaan vastaavan jonon termin
indeksiksi; jokainen jonon termi voidaan siis tunnistaa sen indeksin avulla.
to each term. Se merkitään alaindeksinä ja sitä kutsutaan vastaavan jonon termin
indeksiksi; jokainen jonon termi voidaan siis tunnistaa sen indeksin avulla.
Esimerkkejä
Esimerkki 1: Luonnollisten lukujen jono
Jono  , joka on määritelty kaavalla
, joka on määritelty kaavalla  on nimeltään luonnollisten lukujen jono. Sen ensimmäiset termit ovat:
on nimeltään luonnollisten lukujen jono. Sen ensimmäiset termit ovat:

![]()
Esimerkki 2: Kolmiolukujen jono
Kolmioluvut saavat nimensä seuraavasta geometrisesta periaatteesta: Asetetaan sopiva määrä kolikoita niin, että syntyy yhä suurempia tasasivuisia kolmioita:
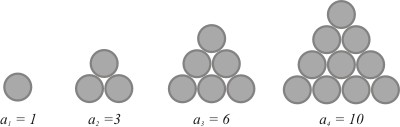
Ensimmäisen kolikon alle lisätään kaksi kolikkoa, jolloin toisessa vaiheessa saadaan  kolikkoa. Seuraavaksi tämän kolmion alle lisätään kolme uutta kolikkoa, joita on nyt yhteensä
kolikkoa. Seuraavaksi tämän kolmion alle lisätään kolme uutta kolikkoa, joita on nyt yhteensä  .
Etenemällä samaan tapaan huomataan, että esimerkiksi 10. kolmioluku saadaan laskemalla yhteen 10 ensimmäistä luonnollista lukua:
.
Etenemällä samaan tapaan huomataan, että esimerkiksi 10. kolmioluku saadaan laskemalla yhteen 10 ensimmäistä luonnollista lukua:
 Yleinen kaava kolmiolukujonon termeille on
Yleinen kaava kolmiolukujonon termeille on  . Kolmioluvuille käytetään yleensä merkintää
. Kolmioluvuille käytetään yleensä merkintää  (T = 'Triangle').
(T = 'Triangle').
Tämä motivoi seuraavaan määritelmään:
Määritelmä: Summajono
Olkoon  jono joukossa
jono joukossa  , jossa on määritelty yhteenlasku. Merkitään
, jossa on määritelty yhteenlasku. Merkitään
 Symboli
Symboli  on kreikkalainen kirjain sigma. Summausindeksi
on kreikkalainen kirjain sigma. Summausindeksi  kasvaa
alkuarvosta 1 loppuarvoon
kasvaa
alkuarvosta 1 loppuarvoon  .
.
Summajono saadaan siis alkuperäisestä jonosta laskemalla alkupään termejä yhteen aina yksi termi eteenpäin. Varsinkin sarjojen kohdalla käytetään nimeä osasummajono.
Kolmiolukujen yleinen kaava voidaan siis kirjoittaa muodossa
 ja kyseessä on luonnollisten lukujen jonon summajono.
ja kyseessä on luonnollisten lukujen jonon summajono.
Esimerkki 3: Neliölukujen jono
Neliölukujen jono  määritellään kaavalla
määritellään kaavalla  . Tämän jonon termejä voidaan havainnollistaa asettelemalla kolikoita neliön muotoon.
. Tämän jonon termejä voidaan havainnollistaa asettelemalla kolikoita neliön muotoon.
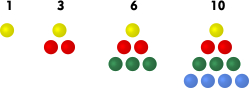
Yksi mielenkiintoinen havainto on se, että kahden peräkkäisen kolmioluvun summa on aina neliöluku. Esimerkiksi  ja
ja  . Yleisesti määritelmiä käyttämällä
voidaan osoittaa, että
. Yleisesti määritelmiä käyttämällä
voidaan osoittaa, että

Esimerkki 4: Kuutiolukujen jono
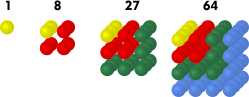
Määritelmä: Erotusjono (differenssijono)
Jonon  termeistä voidaan myös muodostaa peräkkäisten termien erotuksia:
termeistä voidaan myös muodostaa peräkkäisten termien erotuksia:
 on nimeltään alkuperäisen jonon
on nimeltään alkuperäisen jonon  ensimmäinen differenssijono.
ensimmäinen differenssijono.
Ensimmäisen differenssijonon ensimmäinen differenssijono on alkuperäisen jonon toinen differenssijono. sequence. Vastaavalla tavalla määritellään jonon  differenssijono.
differenssijono.
Esimerkki 6.
Eräitä tärkeitä jonoja
Eräät jonot ovat keskeisiä monille matemaattisille malleille ja niiden käytännön sovelluksille muilla aloilla kuten luonnontieteissä ja taloustieteissä.) Seuraavassa tarkastellaan kolme tällaista jonoa: aritmeettinen jono, geometrinen jono ja Fibonaccin lukujono.
Aritmeettinen jono
Aritmeettinen jono voidaan määritellä monella eri tavalla:Määritelmä A: Aritmeettinen jono
Jono  on aritmeettinen, jos sen peräkkäisten termien erotus
on aritmeettinen, jos sen peräkkäisten termien erotus  on vakio, t.s.
on vakio, t.s.

Huomautus: Aritmeettisen jonon eksplisiittinen kaava seuraa suoraan määritelmästä A:
 Aritmeettisen jonon
Aritmeettisen jonon  termi voidaan laskea myös palautuskaavan (eli rekursiokaavan) avulla:
termi voidaan laskea myös palautuskaavan (eli rekursiokaavan) avulla:

Määritelmä B: Aritmeettinen jono
Jono  on aritmeettinen jono, jos sen ensimmäinen differenssijono on vakiojono.
on aritmeettinen jono, jos sen ensimmäinen differenssijono on vakiojono.
Tämä määritelmä selventää myös aritmeettisen jonon nimen: Kolmen peräkkäisen termin keskimmäinen luku on kahden muun termin aritmeettinen keskiarvo; esimerkiksi
Geometrinen jono
Myös geometrisella jonolla on useita erilaisia määritelmiä:
Määritelmä: Geometrinen jono
Jono  on geometrinen, jos kahden präkkäisen termin suhde on aina vakio
on geometrinen, jos kahden präkkäisen termin suhde on aina vakio  , t.s.
, t.s.

Huomautus. Palautuskaava  geometrisen jonon termeille ja myös eksplisiittinen lauseke
geometrisen jonon termeille ja myös eksplisiittinen lauseke
 seuraavat suoraan määritelmästä.
seuraavat suoraan määritelmästä.
Myös tässä jonon nimityksellä on looginen tausta: Kolmen peräkkäisen termin keskimmäinen luku on aina kahden muun termin geometrinen keskiarvo; esimerkiksi

Esimerkki 2.
Olkoon  ja
ja  . Jono
. Jono  , jolle
, jolle  , eli
, eli
 on geometrinen jono. Jos
on geometrinen jono. Jos  ja
ja  , niin jono on aidosti
kasvava. Jos
, niin jono on aidosti
kasvava. Jos  ja
ja  , niin se on aidosti vähenevä. Jonon alkioiden muodostama joukko
, niin se on aidosti vähenevä. Jonon alkioiden muodostama joukko  on äärellinen, jos
on äärellinen, jos  (jolloin sen ainoa alkio on
(jolloin sen ainoa alkio on  ), muuten tämä joukko on ääretön.
), muuten tämä joukko on ääretön.
Fibonaccin jono
Fibonaccin lukujono on kuuluisa sen biologisten sovellusten vuoksi. Se esiintyy mm.eliöiden populaation kasvun yhteydessä ja kasvien rakenteessa. Palautuskaavaan perustuva määritelmä on seuraava:
Määritelmä: Fibonaccin jono
Olkoon  ja
ja
 kun
kun  . Jono
. Jono  on Fibonaccin lukujono. Jonon termit ovat Fibonaccin lukuja.
on Fibonaccin lukujono. Jonon termit ovat Fibonaccin lukuja.
Jonon nimen takana on italialainen Leonardo Pisano (1200-luvulla), latinalaiselta nimeltään Filius Bonacci. Hän tutki kaniparien lisääntymistä idealisoidussa tilanteessa, jossa kanit eivät kuole ja kaikki vanhat sekä uudet parit
lisääntyvät säännöllisin väliajoin. Näin hän päätyi jonoon

Esimerkki 3.
Auringonkukan kukat muodostuvat kahdesta spiraalista, jotka aukeavat keskeltä vastakkaisiin suuntiin: 55 spiraalia myötäpäivään ja 34 vastapäivään.
Myös ananashedelmän pinta käyttäytyy samalla tavalla. Siinä on 21 spiraalia yhteen suuntaan ja 34 vastakkaiseen. Myös joissakin kaktuksissa ja havupuiden kävyissä on samanlaisia rakenteita.

Suppeneminen, hajaantuminen ja raja-arvo
Tässä luvussa käsitellään jonon suppenemista. Aloitamme nollajonon käsitteestä ja siirrymme sen avulla yleiseen suppenemisen käsitteeseen.
Huomautus: Itseisarvo joukossa 
Itseisarvofunktio  on keskeisessä asemassa jonojen suppenemisen tutkimisessa. Seuraavassa käydään läpi sen tärkeimmät ominaisuudet:
on keskeisessä asemassa jonojen suppenemisen tutkimisessa. Seuraavassa käydään läpi sen tärkeimmät ominaisuudet:
Lause: Itseisarvon laskusääntöjä
Kohdat 1.-3. Results follow directly from the definition and by dividing it up into separate cases of the different signs of  and
and 
Kohta 4. Tämä kohta voidaan todistaa neliöön korottamalla tai tutkimalla kaikki eri vaihtoehdot kuten alla.
Tapaus 1.
Olkoot  . Silloin
. Silloin
 ja kaava pätee.
ja kaava pätee.
Tutkitaan lopuksi tapaus  and
and  , joka jakaantuu kahteen alakohtaan:
, joka jakaantuu kahteen alakohtaan:
Jos  ja
ja  , niin väite seuraa samalla periaatteella kuin tapauksessa 3, kun vaihdetaan keskenään
, niin väite seuraa samalla periaatteella kuin tapauksessa 3, kun vaihdetaan keskenään  ja
ja
 .
.
Nollajono
Esimerkki 1.
Jono  , joka on määritelty kaavalla
, joka on määritelty kaavalla  , eli
, eli  on nimeltään harmoninen jono. Jonon termit ovat positiivisia kaikilla
on nimeltään harmoninen jono. Jonon termit ovat positiivisia kaikilla  , mutta indeksin
, mutta indeksin  kasvaessa jonon termit pienenevät yhä lähemmäksi
nollaa.
kasvaessa jonon termit pienenevät yhä lähemmäksi
nollaa.
Jos esimerkiksi  , niin valinnalla
, niin valinnalla  pätee
pätee  aina, kun
aina, kun  .
.
Harmoninen jono suppenee kohti nollaa
Esimerkki 2.
Tarkastellaan jonoa  Olkoon
Olkoon  . Tällöin valinnalla
. Tällöin valinnalla  kaikille termeille
kaikille termeille  , joissa
, joissa  , pätee
, pätee  .
.
Note. Tutkittaessa nollajono-ominaisuutta täytyy tutkia mielivaltaista lukua  , jolle
, jolle  . Sen jälkeen
yritetään valita sellainen indeksi
. Sen jälkeen
yritetään valita sellainen indeksi  , josta alkaen jokainen
, josta alkaen jokainen  on pienempi kuin
on pienempi kuin  .
.
Esimerkki 3.
Kerrointen  vuoksi jonon kaksi peräkkäistä termiä ovat aina erimerkkisiä; tällaista jonoa kutsutaan yleisemmin vuorottelevaksi jonoksi.
vuoksi jonon kaksi peräkkäistä termiä ovat aina erimerkkisiä; tällaista jonoa kutsutaan yleisemmin vuorottelevaksi jonoksi.
Osoitetaan, että kyseessä on nollajono. Määritelmän mukaan jokaista  täytyy vastata sellainen
täytyy vastata sellainen  , että epäyhtälö
, että epäyhtälö
 pätee kaikille niille termeille
pätee kaikille niille termeille  , joissa
, joissa  .
.
Lause: Nollajonojen ominaisuuksia
Parts 1 and 2. If  is a zero sequence, then according to the definition there is an index
is a zero sequence, then according to the definition there is an index  , such that
, such that  for every
for every  and an arbitrary
and an arbitrary  . But then we have
. But then we have  ; this
proves parts 1 and 2 are correct.
; this
proves parts 1 and 2 are correct.
Part 3. If  , then the result is trivial. Let
, then the result is trivial. Let  and choose
and choose  such that
such that
 for all
for all  . Rearranging we get:
. Rearranging we get:

Part 4.
Because  is a zero sequence, by the definition we have
is a zero sequence, by the definition we have  for all
for all  . Analogously,
for the zero sequence
. Analogously,
for the zero sequence  there is a
there is a  with
with  for all
for all  .
.
Then for all  it follows (using the triangle inequality) that:
it follows (using the triangle inequality) that:

Suppeneminen ja hajaantuminen
Nollajonoja voidaan käyttää tutkimaan jonojen suppenemista yleisemmin:
Esimerkki 4.
Tarkastellaan jonoa  , jossa
, jossa
 Laskemalla jonon termejä suurilla
Laskemalla jonon termejä suurilla  , huomataan, että ilmeisesti
, huomataan, että ilmeisesti  , kun
, kun
 , joten jonon raja-arvo voisi olla
, joten jonon raja-arvo voisi olla  .
.
For a rigorous proof, we show that for every  there exists an index
there exists an index  , such that for every term
, such that for every term  with
with  the following relationship holds:
the following relationship holds:

Firstly we estimate the inequality:

Now, let  be an arbitrary constant. We then choose the index
be an arbitrary constant. We then choose the index  , such that
, such that
 Finally from the above inequality we have:
Finally from the above inequality we have:
 Thus we have proven the claim and so by definition
Thus we have proven the claim and so by definition  is
the limit of the sequence.
is
the limit of the sequence.
Jos jono suppenee, niin sillä voi olla vain yksi raja-arvo.
Lause: Raja-arvon yksikäsitteisyys
Oletetaan, että jono  suppenee kohti raja-arvoa
suppenee kohti raja-arvoa  ja kohti raja-arvoa
ja kohti raja-arvoa  .
Silloin
.
Silloin  .
.
Assume  ; choose
; choose  with
with  Then in particular
Then in particular ![[a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset. [a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset.](https://mycourses.aalto.fi/filter/tex/pix.php/4bac60723e473d9697be98685ce7659a.gif)
Because  converges to
converges to  , there is, according to the definition of convergence, a index
, there is, according to the definition of convergence, a index  with
with  for
for  Furthermore, because
Furthermore, because  converges to
converges to  there is also a
there is also a  with
with  for
for  For
For
 we have:
we have:
 Consequently we have obtained
Consequently we have obtained  , which is a contradiction as
, which is a contradiction as  .
Therefore the assumption must be wrong, so
.
Therefore the assumption must be wrong, so  .
.
Suppenevien jonojen ominaisuuksia
Lause: Laskusääntöjä
Olkoot  ja
ja  suppenevia jonoja, joille
suppenevia jonoja, joille  ja
ja  .
Silloin kaikille
.
Silloin kaikille  pätee:
pätee:
Sanallisesti: Suppenevien jonojen summat ja tulot ovat suppenevia jonoja.
Part 1. Let  . We must show, that for all
. We must show, that for all  it follows that:
it follows that:
 The left hand side we estimate using:
The left hand side we estimate using:

Because  and
and  converge, for each given
converge, for each given  it holds true that:
it holds true that:

Therefore
 for all numbers
for all numbers  . Therefore the sequence
. Therefore the sequence
 is a zero sequence and the desired inequality is shown.
is a zero sequence and the desired inequality is shown.
Part 2. Let  . We have to show, that for all
. We have to show, that for all 
 Furthermore an estimation of the left hand side follows:
Furthermore an estimation of the left hand side follows:
 We choose a number
We choose a number  , such that
, such that  for all
for all  and
and  . Such a value of
. Such a value of  exists by the Theorem of convergent sequences being bounded. We can then use the estimation:
exists by the Theorem of convergent sequences being bounded. We can then use the estimation:
 For all
For all  we have
we have
 and
and  , and - putting everything together - the desired inequality it shown.
, and - putting everything together - the desired inequality it shown.
 ';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
/* fibonacci sequence */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox: [-1, 40, 10, -5],
axis: false,
shownavigation: false,
showcopyright: false
});
var xaxis = board.create('axis', [
[0, 0],
[1, 0]
], {
straightFirst: false,
highlight: false,
drawZero: true,
ticks: {
drawLabels: false,
minorTicks: 0,
majorHeight: 15,
label: {
highlight: false,
offset: [0, -15]
}
}
});
var yaxis = board.create('axis', [
[0, 0],
[0, 1]
], {
straightFirst: false,
highlight: false,
ticks: {
minorTicks: 0,
majorHeight: 15,
label: {
offset: [-15, 0],
position: 'lrt',
highlight: false
}
}
});
xaxis.defaultTicks.ticksFunction = function() {
return 1;
};
yaxis.defaultTicks.ticksFunction = function() {
return 5;
};
var a_k = [1, 1];
var newbar = function(k) {
var y;
if (k - 1 > a_k.length - 1) {
y = a_k[k - 3] + a_k[k - 2];
a_k.push(y);
} else {
y = a_k[k - 1];
}
return board.create('polygon', [
[k - 1 / 4, 0],
[k + 1 / 4, 0],
[k + 1 / 4, y],
[k - 1 / 4, y]
], {
vertices: {
visible: false
},
borders: {
strokeColor: 'black',
strokeOpacity: .6,
highlight: false
},
fillColor: '#b2caeb',
fixed: true,
highlight: false
});
}
var bars = [];
for (var i = 0; i < 9; i++) {
const k = i + 1;
board.create('text', [k - .1, -.6, function() {
return '
';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
/* fibonacci sequence */
(function() {
var board = JXG.JSXGraph.initBoard('jxgbox03', {
boundingbox: [-1, 40, 10, -5],
axis: false,
shownavigation: false,
showcopyright: false
});
var xaxis = board.create('axis', [
[0, 0],
[1, 0]
], {
straightFirst: false,
highlight: false,
drawZero: true,
ticks: {
drawLabels: false,
minorTicks: 0,
majorHeight: 15,
label: {
highlight: false,
offset: [0, -15]
}
}
});
var yaxis = board.create('axis', [
[0, 0],
[0, 1]
], {
straightFirst: false,
highlight: false,
ticks: {
minorTicks: 0,
majorHeight: 15,
label: {
offset: [-15, 0],
position: 'lrt',
highlight: false
}
}
});
xaxis.defaultTicks.ticksFunction = function() {
return 1;
};
yaxis.defaultTicks.ticksFunction = function() {
return 5;
};
var a_k = [1, 1];
var newbar = function(k) {
var y;
if (k - 1 > a_k.length - 1) {
y = a_k[k - 3] + a_k[k - 2];
a_k.push(y);
} else {
y = a_k[k - 1];
}
return board.create('polygon', [
[k - 1 / 4, 0],
[k + 1 / 4, 0],
[k + 1 / 4, y],
[k - 1 / 4, y]
], {
vertices: {
visible: false
},
borders: {
strokeColor: 'black',
strokeOpacity: .6,
highlight: false
},
fillColor: '#b2caeb',
fixed: true,
highlight: false
});
}
var bars = [];
for (var i = 0; i < 9; i++) {
const k = i + 1;
board.create('text', [k - .1, -.6, function() {
return ' ';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
';
}], {
useMathJax: true,
strokeColor: '#2183de',
fontSize: 13,
fixed: true,
highlight: false
});
board.fullUpdate();
})();
';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
board.create('point', [i, 1 / i], {
size: 4,
name: '',
strokeWidth: .5,
strokeColor: 'black',
face: 'diamond',
fillColor: '#cf4490',
fixed: true
});
}
board.fullUpdate();
})();
';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
bars.push(newbar(k));
}
board.fullUpdate();
})();
';
}], {
useMathJax: true,
strokeColor: '#2183de',
fontSize: 13,
fixed: true,
highlight: false
});
board.fullUpdate();
})();
';
}], {
useMathJax: true,
fixed: true,
strokeOpacity: 0.6
});
board.create('point', [i, 1 / i], {
size: 4,
name: '',
strokeWidth: .5,
strokeColor: 'black',
face: 'diamond',
fillColor: '#cf4490',
fixed: true
});
}
board.fullUpdate();
})();


























































































