MS-A0111 - Differential and Integral Calculus 1, Lecture, 13.9.2021-27.10.2021

Table of Content

• Derivative
• Properties of derivative
• Derivatives of Trigonometric Functions
• The Chain Rule
• Extremal Value Problems

Derivative

---

The definition of the derivative of a function is given next. We start with an example illustrating the idea behind the formal definition.

Example 0.

The graph below shows how far a cyclist gets from his starting point.

a) Look at the red line. We can see that in three hours, the cyclist moved $20$km. The average speed of the whole trip is $6.6$ km/h.
b) Now look at the green line. We can see that during the third hour the cyclist moved $10$km further. That makes the average speed of that time interval $10$ km/h.
Notice that the slope of the red line is $20/3 \approx 6.6$ and that the slope of the blue line is $10$. These are the same values as the corresponding average speeds.
c) Look at the blue line. It is the tangent of the curve at the point $x=2h$. Using the same principle as with average speeds, we conclude that after two hours of the departure, the speed of the cyclist was $30/2$ km/h $= 15$ km/h.

Now we will proceed to the general definition:

Definition: Derivative

Let $(a,b)\subset \mathbb{R}$. The derivative of function $f\colon (a,b)\to \mathbb{R}$ at the point $x_0\in (a,b)$ is $f'(x_0):=\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}.$ If $f'(x_0)$ exists, then $f$ is said to be differentiable at the point $x_0$.

Note: Since $x = x_0+h$, then $h=x-x_0$, and thus the definition can also be written in the form $f'(x_0):=\lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}.$

The derivative can be denoted in different ways: $f'(x_0)=Df(x_0) =\left. \frac{df}{dx}\right|_{x=x_0}, \ \ f'=Df =\frac{df}{dx}.$

Interpretation. Consider the curve $y = f(x)$. Now if we draw a line through the points $(x_0,f(x_0))$ and $(x_0+h, f(x_0+h))$, we see that the slope of this line is $\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0} = \frac{f(x_0+h)-f(x_0)}{h}.$ When $h \to 0$, the line intersects with the curve $y = f(x)$ only in the point $(x_0, f(x_0))$. This line is the tangent of the curve $y=f(x)$ at the point $(x_0,f(x_0))$ and its slope is $\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h},$ which is the derivative of the function $f$ at $x_0$. Hence, the tangent is given by the equation $y=f(x_0)+f'(x_0)(x-x_0).$

Interactivity. Move the point of intersection and observe changes on the tangent line of the curve.

Example 1.

Let $f\colon \mathbb{R} \to \mathbb{R}$ be the function $f(x) = x^3 + 1$. The derivative of $f$ at $x_0 = 1$ is $\begin{aligned}f'(1) &=\lim_{h \to 0} \frac{f(1+h)-f(1)}{h} \\ &=\lim_{h \to 0} \frac{(1+h)^3 + 1 - 1^3 - 1}{h} \\ &=\lim_{h \to 0} \frac{1+3h+3h^2+h^3-1}{h} \\ &=\lim_{h \to 0} \frac{h(3+3h+h^2)}{h} \\ &=\lim_{h \to 0} 3+3h+h^2 \\ &= 3. \end{aligned}$

Example 2.

Let $f\colon \mathbb{R} \to \mathbb{R}$ be the function $f(x)=ax+b$. We find the derivative of $f(x)$.

Immediately from the definition we get: $\begin{aligned}f'(x) &=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to 0} \frac{[a(x+h)+b]-[ax+b]}{h} \\ &=\lim_{h\to 0} a \\ &=a.\end{aligned}$

Here $a$ is the slope of the tangent line. Note that the derivative at $x$ does not depend on $x$ because $y=ax+b$ is the equation of a line.

Note. When $a=0$, we get $f(x) = b$ and $f'(x) = 0$. The derivative of a constant function is zero.

Example 3.

Let $g\colon \mathbb{R} \to \mathbb{R}$ be the function $g(x)=|x|$. Does $g$ have a derivative at $0$?

Now $g'(x_0)= \begin{cases}+1 & \text{when $x_{0}>0$} \\ -1 & \text{when $x_{0}$

The graph $y=g(x)$ has no tangent at the point $x_0=0$: $\frac{g(0+h)-g(0)}{h}= \frac{|0+h|-|0|}{h}=\frac{|h|}{h}=\begin{cases}+1 & \text{for $h>0$}, \\ -1 & \text{for $h$ Thus $g'(0)$ does not exist.

Conclusion. The function $g$ is not differentiable at the point $0$.

Remark. Let $f\colon (a,b)\to \mathbb{R}$. If $f'(x)$ exists for every $x\in (a,b)$ then we get a function $f'\colon (a,b)\to \mathbb{R}$. We write:

(1)	$f(x)$	= $f^{(0)}(x)$,
(2)	$f'(x)$	=  $f^{(1)}(x)$	=  $\frac{d}{dx}f(x)$,
(3)	$f''(x)$	=  $f^{(2)}(x)$	=  $\frac{d^2}{dx^2}f(x)$,
(4)	$f'''(x)$	=  $f^{(3)}(x)$	=  $\frac{d^3}{dx^3}f(x)$,
...

Here $f''(x)$ is called the second derivative of $f$ at $x$, $f^{(3)}$ is the third derivative, and so on.

We introduce the notation \begin{eqnarray} C^n\bigl( ]a,b[\bigr) =\{ f\colon \, ]a,b[\, \to \mathbb{R} & \mid & f \text{ is } n \text{ times differentiable on the interval } ]a,b[ \nonumber \\ & & \text{ and } f^{(n)} \text{ is continuous}\}. \nonumber \end{eqnarray} These functions are said to be n times continuously differentiable.

Example 4.

The distance moved by a cyclist (or a car) is given by $s(t)$. Then the speed at the moment $t$ is $s'(t)$ and the acceleration is $s''(t)$.

Linearization and differential

Derivative can also be used to approximate functions. From the definition of the derivative, we get $f'(x_0)\approx \frac{f(x)-f(x_0)}{x-x_0} \Leftrightarrow f(x)\approx f(x_0)+f'(x_0)(x-x_0),$ where the right-handed side is the linearization or the differential of $f$ at $x_0$. The differential is denoted by $df$. The graph of the linearization, $y=f(x_0)+f'(x_0)(x-x_0),$ is the tangent line drawn on the graph of the function $f$ at the point $(x_0,f(x_0))$. Later, in multi-variable calculus, the true meaning of the differential becomes clear. For now, it is not necessary to get troubled by the details.

Properties of derivative

---

Next we give some useful properties of the derivative. These properties allow us to find derivatives for some familiar classes of functions such as polynomials and rational functions.

Continuity and derivative

If $f$ is differentiable at the point $x_0$, then $f$ is continuous at the point $x_0$: $\lim_{h\to 0} f(x_0+h) = f(x_0).$ Why? Because if $f$ is differentiable, then we get $f(x_0)+h\frac{f(x_0+h)-f(x_0)}{h} \rightarrow f(x_0)+0\cdot f'(x_0)=f(x_0),$ as $h \to 0$.

Note. If a function is continuous at the point $x_0$, it doesn't have to be differentiable at that point. For example, the function $g(x) = |x|$ is continuous, but not differentiable at the point $0$.

Differentiation Rules

Next we will give some important rules which are often applied in practical problems concerning determination of the derivative of a given function.

Suppose that $f$ and $g$ are differentiable at $x$.

A Constant Multiplier

$(cf)'(x) = cf'(x),\ c \in \mathbb{R}$

Proof.

Suppose that $f$ is differentiable at $x$. We determine: $(cf)'(x),$ where $c\in \mathbb{R}$ is a constant.

$\begin{aligned}\frac{(cf)(x+h)-(cf)(x)}{h} \ & \ = \ \frac{cf(x+h)-cf(x)}{h} \\ & \ = \ c \ \frac{f(x+h)-f(x)}{h}\end{aligned}$

As $h\to 0$, we get $c \ \frac{f(x+h)-f(x)}{h} \to c f'(x).$

$\square$

The Sum Rule

$(f+g)'(x) = f'(x) + g'(x)$

Proof.

Suppose that $f$ and $g$ are differentiable at $x$. We determine $(f+g)'(x).$

By the definition: $\begin{aligned}\frac{(f+g)(x+h)-(f+g)(x)}{h} \ & \ = \ \frac{[f(x+h)+g(x+h)]-[f(x)+g(x)]}{h} \\ & \ = \ \frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\end{aligned}$

When $h\to 0$, we get $\frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\to \ f'(x)+g'(x)$

$\square$

The Product Rule

$(fg)'(x) = f'(x)g(x) + f(x)g'(x)$

Proof.

Suppose that $f,g$ and are differentiable at $x$. We determine $(fg)'(x).$ $\begin{aligned}\frac{(fg)(x+h)-(fg)(x)}{h} & = \frac{f(x+h)g(x+h)-f(x)g(x)}{h} \\ & = \frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h} \\ & = \frac{f(x+h)-f(x)}{h}\ g(x+h)+f(x)\ \frac{g(x+h)-g(x)}{h}\end{aligned}$

When $h\to 0$, we get $\frac{f(x+h)-f(x)}{h}g(x+h)+f(x)\frac{g(x+h)-g(x)}{h}\to f'(x)g(x)+f(x)g'(x).$

$\square$

The Power Rule

$\frac{d}{dx} x^n = nx^{n-1} \text{, } n \in \mathbb{Z}$

Proof.

For $n\ge 1$ we repeteadly apply the product rule, and obtain $\begin{aligned}\frac{d}{dx}x^n \ & = \frac{d}{dx}(x\cdot x^{n-1}) \\ & = (\frac{d}{dx}x)x^{n-1}+x\frac{d}{dx}x^{n-1} \\ & \stackrel{dx/dx=1}{=} x^{n-1}+x\frac{d}{dx}x^{n-1} \\ & = x^{n-1}+x\left( x^{n-2}+x\frac{d}{dx}x^{n-2}\right) \\ & = \ldots \\ & = \sum_{k=0}^{n-1} x^{n-1} \\ & = nx^{n-1}.\end{aligned}$

The case of negative $n$ is obtained from this and the product rule applied to the identity $x^n \cdot x^{-n} = 1$.

From the power rule we obtain a formula for the derivative of a polynomial. Let $P(x)=a_n x^{n}+a_{n-1}x^{n-1}+\ldots+ a_1 x + a_0,$ where $n\in \mathbb{N}$. Then $\frac{d}{dx}P(x)=na_nx^{n-1}+(n-1)a_{n-1}x^{n-2}+\ldots +2 a_2 x+a_1.$

$\square$

The Reciprocal Rule

$\Big(\frac{1}{f}\Big)'(x) = - \frac{f'(x)}{f(x)^2} \text{, } f(x) \neq 0$

Proof.

Suppose that $f$ is differentiable at $x$ and $f(x)\neq 0$. We determine $(\frac{1}{f})'(x).$

From the definition we obtain: $\begin{aligned}\frac{(1/f)(x+h)-(1/f)(x)}{h} & = \frac{1/f(x+h)-1/f(x)}{h} \\ & = \frac{\frac{f(x)}{f(x)f(x+h)}-\frac{f(x+h)}{f(x)f(x+h)}}{h} \\ & = \frac{f(x)-f(x+h)}{h}\frac{1}{f(x)f(x+h)}\end{aligned}$

Because $f$ is differentiable at $x$ we get $\frac{f(x)-f(x+h)}{h}\frac{1}{f(x)f(x+h)}=-f'(x)/f(x)^2,$ as $h\to 0$.

$\square$

The Quotient Rule

$(f/g)'(x) = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2},\ g(x) \neq 0$

Proof.

Suppose that $f,g$ are differentiable at $x$ and $g(x)\neq 0$. Then $\begin{aligned}(f/g)'(x) & = \Big( f \cdot \frac{1}{g}\Big) '(x) \\ & = f'(x)\frac{1}{g(x)}-f(x)\frac{g'(x)}{g(x)^2} \\ & = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}.\end{aligned}$

$\square$

Example 1.

$\frac{d}{dx}(x^{2006}+5x^3+42)=\frac{d}{dx}x^{2006}+5\frac{d}{dx}x^3+42\frac{d}{dx}1=2006x^{2005}+5\cdot 3x^2.$

Example 2.

$\begin{aligned}\frac{d}{dx} [(x^4-2)(2x+1)] &= \frac{d}{dx}(x^4-2) \cdot (2x+1) + (x^4-2) \cdot \frac{d}{dx}(2x + 1) \\ &= 4x^3(2x+1) + 2(x^4-2) \\ &= 8x^4+4x^3+2x^4-4 \\ &= 10x^4+4x^3-4.\end{aligned}$

Note. We can check the answer by deriving it in another way: $\frac{d}{dx} [(x^4-2)(2x+1)] = \frac{d}{dx} (2x^5 +x^4 -4x -2) = 10x^4 +4x^3 -4.$

Example 3.

For $x \neq 0$ we get $\frac{d}{dx} \frac{3}{x^3} = 3 \cdot \frac{d}{dx} \frac{1}{x^3} = -3 \cdot \frac{\frac{d}{dx} x^3}{(x^3)^2} = -3 \cdot \frac{3x^2}{x^6}= - \frac{9}{x^4}.$

Note. There is another way of solving the problem above by noticing that $\frac{1}{x^3} = x^{-3}$ and differentiating it as a power: $\frac{d}{dx} \ \frac{3}{x^3} = 3 \cdot \frac{d}{dx} x^{-3} = 3 \cdot (-3x^{-4})= - \frac{9}{x^4}$

Example 4.

$\begin{aligned}\frac{d}{dx} \frac{x^3}{1+x^2} & = \frac{(\frac{d}{dx}x^3)(1+x^2)-x^3\frac{d}{dx}(1+x^2)}{(1+x^2)^2} \\ & = \frac{3x^2(1+x^2)-x^3(2x)}{(1+x^2)^2} \\ & = \frac{3x^2+x^4}{(1+x^2)^2}.\end{aligned}$

Rolle's Theorem

If $f$ is differentiable at a local extremum $x_0\in \, ]a,b[$, then $f'(x_0)=0$.

Proof (idea).

The one-sided limits of the difference quotient have different signs at a local extremum. For example, for a local maximum it holds that \begin{eqnarray} \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative} }{\text{positive}}&\le& 0, \text{ when } h>0, \nonumber \\ \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative}}{\text{negative}}&\ge& 0, \text{ when } h<0 \nonumber \end{eqnarray} and $|h|$ is so small that $f(x_0)$ is a maximum on the interval $[x_0-h,x_0+h]$.

L'Hospital's Rule

There are many different versions of this rule, but we present only the simplest one. Let us assume that $f(x_0)=g(x_0)=0$ and the functions $f,g$ are differentiable on some interval $]x_0-\delta,x_0+\delta[$. If $\lim_{x\to x_0}\frac{f'(x)}{g'(x)}$ exists, then $\lim_{x\to x_0}\frac{f(x)}{g(x)}=\lim_{x\to x_0}\frac{f'(x)}{g'(x)}.$

Proof (idea).

In the special case $g'(x_0)\neq 0$ the proof is simple: $\frac{f(x)}{g(x)}=\frac{f(x)-f(x_0)}{g(x)-g(x_0)} = \frac{\bigl( f(x)-f(x_0)\bigr) /(x-x_0)}{\bigl( g(x)-g(x_0)\bigr) /(x-x_0)} \to \frac{f'(x_0)}{g'(x_0)}.$ In the general case we need the so-called generalized mean value theorem, which states that $\frac{f(x)}{g(x)} = \frac{f'(c)}{g'(c)}$ for some $c\in \, ]x_0,x[$. Here we have the same point $c$ both in the numerator and the denominator, so we do not even need the continuity of the derivatives!

Derivatives of Trigonometric Functions

---

In this section, we give differentiation formulas for trigonometric functions $\sin$, $\cos$ and $\tan$.

Derivative of Sine

$\sin'(t)=\cos(t)$

Proof.

From the definition of the derivative and trigonometric identity for $\sin(t+h)$:

$\begin{aligned}\sin'(t) & = \lim_{h\to 0} \frac{\sin(t+h)-\sin(t)}{h} \\ & = \lim_{h\to 0} \frac{[\sin(t)\cos(h)+\cos(t)\sin(h)]-\sin(t)}{h} \\ & = \lim_{h\to 0}\sin(t)\frac{\cos(h)-1}{h}+\lim_{h\to 0}\cos(t)\frac{\sin(h)}{h}. \end{aligned}$

Here $\lim_{h\to 0}\frac{\sin h}{h} = 1$ by a geometrical argument, and

$\frac{\cos h-1}{h} = \frac{\cos^2 h-1}{h(\cos h+1)} = -\frac{\sin h}{h}\cdot \frac{\sin h}{\cos h+1} \to -1\cdot 0 = 0$

as $h\to 0$.

Hence we have $\sin'(t)=\cos(t).$

$\square$

Derivative of Cosine

$\cos'(t)= - \sin(t)$

Proof.

This follows in a similar way as the derivative of Sine, but more easily from the identity $\cos(t)=\sin(\pi/2-t)$ and the Chain rule to be introduced in the following section.

$\square$

Function $\cos(x)$ and its derivative function $-\sin(x)$.

Derivative of Tangent

$\tan'(t) = \frac{1}{\cos^2(t)}=1+\tan^2 t.$

Proof.

Because $\tan(t)=\frac{\sin(t)}{\cos(t)},$ from the quotient rule we obtain $\tan'(t)=\frac{\sin'(t)\cos(t)-\sin(t)\cos'(t)}{\cos^2(t)}=\frac{\cos^2(t)+\sin^2(t)}{\cos^2(t)}=\begin{cases}\frac{1}{\cos^2(t)} & \\ 1+\tan^2 t.\end{cases}$

$\square$

Example 1.

$\frac{d}{dx} (3 \sin(x)) = 3 \sin'(x) = 3 \cos(x).$

Example 2.

$\frac{d}{dx} \cos^2 (x) = \cos'(x) \cdot \cos(x) + \cos(x) \cdot \cos'(x) = -2\sin(x)\cos(x).$

Example 3.

$\begin{aligned} \frac{d}{dx} \frac{\sin(x) + 1}{\cos(x)} &= \frac{d}{dx} \left( \frac{\sin(x)}{\cos(x)} + \frac{1}{\cos(x)} \right) \\ &= \tan'(x) - \frac{\cos'(x)}{\cos^2(x)} \\ &= \frac{1+\sin(x)}{\cos^2 (x)}.\end{aligned}$

The Chain Rule

---

In this section we learn a formula for finding the derivative of a composite function. This important formula is known as the Chain Rule.

The Chain Rule.

Let $f\colon \mathbb{R}\to \mathbb{R}$, $g\colon \mathbb{R}\to \mathbb{R}$ and $f \circ g \colon \mathbb{R}\to \mathbb{R}$.

Let $g$ be differentiable at the point $x$ and $f$ at $g(x)$. Then $\frac{d}{dx}f(g(x))=f'(g(x))g'(x).$

Proof.

Consider

$\begin{aligned}\frac{f(g(x+h))-f(g(x))}{h} &= \frac{f(g(x+h))-f(g(x))}{h} \ \frac{g(x+h)-g(x)}{g(x+h)-g(x)} \\ &= \frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)} \ \frac{g(x+h)-g(x)}{h}.\end{aligned}$

Now let us write $k(h):=g(x+h)-g(x)$. Then $g(x+h)=g(x)+k(h)$ and we get $\frac{f(g(x+h))-f(g(x))}{h}=\frac{f(g(x)+k(h))-f(g(x))}{k(h)}\frac{g(x+h)-g(x)}{h}.$

Problem. What if $k(h)=0$? Note that one cannot divide by zero.

Solution. Define $E(k):= \begin{cases}0, & \text{for $k=0$}, \\ \frac{f(g(x)+k)-f(g(x))}{k}-f'(g(x)), & \text{for $k\neq 0$},\end{cases}$ so that $\frac{f(g(x+h))-f(g(x))}{h}=[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}.$ Now, because $E$ is continuous, we get $[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}\to f'(g(x))g'(x).$ as $h\to 0$.

$\square$

Example 1.

The problem is to differentiate the function $(2x-1)^3$. We take $f(x) = x^3$ and $g(x) = 2x-1$ and differentiate the composite function $f(g(x))$. As $f'(x) = 3x^2 \text{ and } g'(x) = 2,$ we get $\frac{d}{dx} (2x-1)^3 = 3(2x-1)^2 \cdot 2 = 6(4x^2-4x+1) = 24x^2-24x+6.$

Example 2.

We need to differentiate the function $\sin 3x$. Take $f(x) = \sin x$ and $g(x) = 3x$, then differentiate the composite function $f(g(x))$. $\frac{d}{dx} \sin 3x = \cos 3x \cdot 3 = 3 \cos 3x.$

Remark. Let $h\colon \mathbb{R}\to \mathbb{R}, g\colon \mathbb{R}\to \mathbb{R}$ and $f\colon \mathbb{R}\to \mathbb{R}$. Now $\frac{d}{dx}f(g(h(x)))=f'(g(h(x)))\frac{d}{dx}g(h(x))=f'(g(h(x)))g'(h(x))h'(x).$ Similarly, one may obtain even more complex rules for composites of multiple functions.

Example 3.

Differentiate the function $\cos^3 2x$. Take $f(x) = x^3$, $g(x) = \cos x$ and $h(x) = 2x$ and differentiate the composite function $f(g(h(x)))$. $\begin{aligned}\frac{d}{dx} \cos^3 2x &= 3(\cos 2x)^2 \cdot \frac{d}{dx} \cos 2x \\ &= 3 \cos^2 2x \cdot (-\sin 2x) \cdot 2 \\ &= -6 \sin 2x \cos^2 2x.\end{aligned}$

Extremal Value Problems

---

We will discuss the Intermediate Value Theorem for differentiable functions, and its connections to extremal value problems.

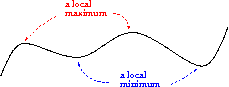
Definition: Local Maxima and Minima

A function $f\colon A\to \mathbb{R}$ has a a local maximum at the point $x_0\in A$, if for some $h\gt 0$ and for all $x\in A$ such that $|x-x_0|\lt h$, we have $f(x)\leq f(x_0)$.

Similarly, a function $f\colon A\to \mathbb{R}$ has a local minimum at the point $x_0\in A$ , if for some $h>0$ and for all $x\in A$ such that $|x-x_0|\lt h$, we have $f(x)\geq f(x_0)$.

A local extreme is a local maximum or a local minimum.

Remark. If $x_0$ is a local maximum value and $f'(x_0)$ exists, then $\begin{cases}f'(x_0) & =\lim_{h\to 0^{+}}\frac{f(x_0+h)-f(x_0)}{h} \leq 0 \\ f'(x_0) & =\lim_{h\to 0^{-}}\frac{f(x_0+h)-f(x_0)}{h} \geq 0.\end{cases}$ Hence $f'(x_0)=0$.

We get:

Theorem 1.

Let $x_0\in [a,b]$ be a local extremal value of a continuous function $f\colon [a,b]\to \mathbb{R}$. Then either

1. the derivative $f'(x_0)$ doesn't exist (this includes also cases $x_0=a$ and $x_0=b$) or

2. $f'(x_0)=0$.

Example 1.

Let $f: \mathbb{R} \to \mathbb{R}$ be defined by $f(x) = x^3 -3x + 1.$ Then $f'(x) = 3x^2-3$ and we can see that at the points $x_0 = -1$ and $x_0 = 1$ the local maximum and minimum of $f$ are obtained, $f'(-1) = 3 \cdot (-1)^2 - 3 = 0 \text{ and } f'(1) = 3 \cdot 1^2 - 3 = 0.$

Finding the global extrema

In practice, when we are looking for the local extrema of a given function, we need to check three kinds of points:

1. the zeros of the derivative

2. the endpoints of the domain of definition (interval)

3. points where the function is not differentiable

If we happened to know beforehand that the function has a minimum/maximum, then we start off by finding all the possible local extrema (the points described above), evaluate the function at these points and pick the greatest/smallest of these values.

Example 2.

Let us find the smallest and greatest value of the function $f\colon [0,2]\to \mathbf{R}$, $f(x)=x^3-6x$. Since the function is continuous on a closed interval, then it has a maximum and a minimum. Since the function is differentiable, it is sufficient to examine the endpoints of the interval and the zeros of the derivative that are contained in the interval.

The zeros of the derivative: $f'(x)=3x^2-6=0 \Leftrightarrow x=\pm \sqrt{2}$. Since $-\sqrt{2}\not\in [0,2]$, we only need to evaluate the function at three points, $f(0)=0$, $f(\sqrt{2})=-4\sqrt{2}$ and $f(2)=-4$. From these we can see that the smallest value of the function is $-4\sqrt{2}$ and the greatest value is $0$, respectively.

Next we will formulate a fundamental result for differentiable functions. The basic idea here is that the change on an interval can only happen, if there is change at some point on the inverval.

Theorem 2.

(The Intermediate Value Theorem for Differentiable Functions). Let $f\colon [a,b]\to \mathbb{R}$ be continuous in the interval $[a,b]$ and differentiable in the interval $(a,b)$. Then $f'(x_0)=\frac{f(b)-f(a)}{b-a}$ for some $x_0\in (a,b).$

Proof.

Let $f$ be continuous in the interval $[a,b]$ and differentiable in the interval $(a,b)$. Let us define $g(x):=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)-f(a).$

Now $g(a)=g(b)=0$ and $g$ is differentiable in the interval $(a,b)$. According to Rolle's Theorem, there exists $c\in(a,b)$ such that $g'(c)=0$. Hence $f'(c)=g'(c)+\frac{f(b)-f(a)}{b-a}=\frac{f(b)-f(a)}{b-a}.$

$\square$

This result has an important application:

Theorem 3.

Let $f\colon (a,b)\to \mathbb{R}$ be a differentiable function. Then

1. If for all $x\in (a,b) \ \ f'(x)\geq 0$, then $f$ is increasing,

2. If for all $x\in (a,b) \ \ f'(x)\leq 0$, then $f$ is decreasing.

Proof.

Suppose that $a \lt x_1 \lt x_2 \lt b$.

Then by Theorem 2 there exists $x_0\in (x_1,x_2)$ such that $f'(x_0)=\frac{f(x_2)-f(x_1)}{x_2-x_1}.$

It follows that $f(x_2)-f(x_1)=f'(x_0)(x_2-x_1)$.

Hence we may conclude that $f$ is increasing for $f'(x_0)\geq 0$ and decreasing for $f'(x_0)\leq 0$.

Example 3.

For the polynomial $f(x) = \frac{1}{4} x^4-2x^2-7$ the derivative is $f'(x) = x^3-4x = x(x^2-4) = 0,$ when $x=0$, $x=2$ or $x=-2$. Now we can draw a table:

	$x$	$-2 \lt x \lt 0$	$0 \lt x \lt 2$	$x>2$
$x$			$>0$	$>0$
$x^2-4$	$>0$			$>0$
$f'(x)$		$>0$		$>0$
$f(x)$	decr.	incr.	decr.	incr.

Example 4.

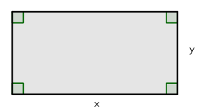
We need to find a rectangle so that its area is $9$ and it has the least possible perimeter.

Let $x\ (>0)$ and $y\ (>0)$ be the sides of the rectangle. Then $x \cdot y = 9$ and we get $y=\frac{9}{x}$. Now the perimeter is $2x+2y = 2x+2 \frac{9}{x} = \frac{2x^2+18}{x}.$ In which point does the function $f(x) = \frac{2x^2+18}{x}$ get its minimum value? Function $f$ is continuous and differentiable, when $x>0$ and using the quotient rule, we get $f'(x) = \frac{4x \cdot x-(2x^2+18) \cdot 1}{x^2} = \frac{2x^2-18}{x^2}.$ Now $f'(x) = 0$, when $\begin{aligned}2x^2-18 &= 0 \\ 2x^2 &= 18 \\ x^2 &= 9 \\ x &= \pm 3\end{aligned}$ but we have defined that $x>0$ and therefore are only interested in the case $x=3$. Let's draw a table:

	$x$	$x>3$
$f'(x)$		$>0$
$f(x)$	decr.	incr.

As the function $f$ is continuous, we now know that it attains its minimum at the point $x=3$. Now we calculate the other side of the rectangle: $y=\frac{9}{x}=\frac{9}{3}=3$.

Thus, the rectangle, which has the least possible perimeter is actually a square, which sides are of the length $3$.

Example 5.

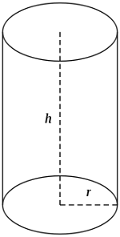
We must make a one litre measure, which is shaped as a right circular cylinder without a lid. The problem is to find the best size of the bottom and the height so that we need the least possible amount of material to make the measure.

Let $r > 0$ be the radius and $h > 0$ the height of the cylinder. The volume of the cylinder is $1$ dm$^3$ and we can write $\pi r^2 h = 1$ from which we get $h = \frac{1}{\pi r^2}.$

The amount of material needed is the surface area $A_{\text{bottom}} + A_{\text{side}} = \pi r^2 + 2 \pi r h = \pi r^2 + \frac{2 \pi r}{\pi r^2} = \pi r^2 + \frac{2}{r}.$

Let function $f: (0, \infty) \to \mathbb{R}$ be defined by $f(r) = \pi r^2 + \frac{2}{r}.$ We must find the minimum value for function $f$, which is continuous and differentiable, when $r>0$. Using the reciprocal rule, we get $f'(r) = 2\pi r -2 \cdot \frac{1}{r^2} = \frac{2\pi r^3 - 2}{r^2}.$ Now $f'(r) = 0$, when $\begin{aligned}2\pi r^3 - 2 &= 0 \\ 2\pi r^3 &= 2 \\ r^3 &= \frac{1}{\pi} \\ r &= \frac{1}{\sqrt[3]{\pi}}.\end{aligned}$

Let's draw a table:

	$r$	$r>\frac{1}{\sqrt[3]{\pi}}$
$f'(r)$		$>0$
$f(r)$	decr.	incr.

As the function $f$ is continuous, we now know that it gets its minimum value at the point $r= \frac{1}{\sqrt[3]{\pi}} \approx 0.683$. Then $h = \frac{1}{\pi r^2} = \frac{1}{\pi \left(\frac{1}{\sqrt[3]{\pi}}\right)^2} = \frac{1}{\frac{\pi}{\pi^{2/3}}} = \frac{1}{\sqrt[3]{\pi}} \approx 0.683.$

This means that it would take least materials to make a measure, which is approximately $2 \cdot 0.683$ dm $= 1.366$ dm $\approx 13.7$ cm in diameter and $0.683$ dm $\approx 6.8$ cm high.

', strokeColor : '#b942f5', fillColor : 'black', strokeWidth : 1, fillOpacity : .5, showinfobox : false, label : { useMathJax : true } }); board.create('segment', [x0,function() { return [x0.X(),f(x0.X())]; }], { dash : 1, strokeColor : '#b942f5' }); var g1 = board.create('glider', [function() { return x0.X(); }, function() { return f(x0.X()); }, graph], { visible : false }); var t = board.create('tangent', [g1], { strokeWidth : 1.5, strokeColor : '#b942f5' }); board.create('line', [[function() { return x0.X(); }, function() { return f(x0.X()); }], [function() { return x0.X()+.7; }, function() { return f(x0.X()+.7); }]], { strokeOpacity : .5, strokeWidth : 1.5 }); board.create('line', [[function() { return x0.X(); }, function() { return f(x0.X()); }], [function() { return x0.X()+1.4; }, function() { return f(x0.X()+1.4); }]], { strokeOpacity : .5, strokeWidth : 1.5 }); board.create('line', [[function() { return x0.X(); }, function() { return f(x0.X()); }], [function() { return x0.X()+2.1; }, function() { return f(x0.X()+2.1); }]], { strokeOpacity : .5, strokeWidth : 1.5 }); board.fullUpdate(); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox02', { boundingbox : [-5, 7, 5, -4], shownavigation : false, axis : true }); var f = function(x) { return x*x*x+2*x*x; } var graph = board.create('functiongraph', [f, -5, 5], { strokeWidth : 2, strokeColor : 'black' }); var g1 = board.create('glider', [.5, f(.5), graph], { strokeWidth : 1, size : 5.5, strokeColor : 'black', fillColor : 'gray', name : '$df$', label : { strokeColor : 'blue' } }); var t = board.create('tangent', [g1], { strokeWidht : 2, strokeOpacity : .8 }); var text1 = board.create('text', [-4, 5, function() { return '$f(x) = x^3+2x^2$'}], { useMathJax : true, fontSize : 14, strokeColor : 'black' }); var text2 = board.create('text', [-4, 4, function() { var k = t.getSlope(); var b = g1.Y()-k*g1.X(); var temp = ''; if(k == 0) { temp = '$df=' + b.toFixed(2) +'$'; } else { if(b < 0) { temp = '$df=' + k.toFixed(2) + 'x' + b.toFixed(2) + '$'; } else { temp = '$df=' + k.toFixed(2) + 'x + ' + b.toFixed(2) + '$'; } } return temp; } ], { useMathJax : true, fontSize : 14, strokeColor : 'blue' }); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox03', { boundingbox : [-3.5, 3, 3.5, -3], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0],[1, 0]], { ticks : { majorHeight : 5 } }); var yaxis = board.create('axis' ,[[0, 0],[0, 1]], { ticks : { majorHeight : 5} }); var f = function(x) { return x*x*x+1; } var graph = board.create('functiongraph', [f, -3.5, 3.5], { strokeWidth : 1.5, strokeColor : 'black' }); var g1 = board.create('glider', [1, f(1), graph], { strokeColor : 'black', size : 2, fillColor : 'red', name : '' }); var t = board.create('tangent', [g1], { strokeColor : 'red', strokeWidth : 1.5 }); var a = board.create('segment', [[function() { return g1.X() }, function() { return g1.Y()-t.getSlope(); }], [function() { return g1.X()-1; }, function() { return g1.Y()-t.getSlope() }]], { strokeWidth : 2, strokeOpacity : .8, dash : 1, highlight : false }); var b = board.create('segment', [[ function() { return g1.X(); }, function() { return g1.Y(); }], [ function() { return a.point1.X(); }, function() { return a.point1.Y(); } ]], { strokeWidth : 2, strokeOpacity : .8, dash : 1, highlight : false }); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox04', { boundingbox : [-5, 5, 5, -2], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); xaxis.defaultTicks.ticksFunction = function() { return 1; }; yaxis.defaultTicks.ticksFunction = function() { return 1; }; var f = function(x) { return Math.abs(x); } board.create('functiongraph', [f, -5, 5], { strokeWidth : 2, strokeColor : '#2183de', highlight : false }); board.create('text', [1.5, 1.2, function() { return '$f(x)=|x|$'; }], { useMathJax : true, strokeColor : '#2183de', fontSize : 13, fixed : true, highlight : false }); board.fullUpdate(); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox05', { boundingbox : [-1.7, 10.1, 1.7, -10.1], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); xaxis.defaultTicks.ticksFunction = function() { return 1; }; yaxis.defaultTicks.ticksFunction = function() { return 5; }; var f = function(x) { return (x*x*x*x-2)*(2*x+1); } board.create('functiongraph', [f, -1.7, 1.7], { strokeWidth : 2.5, strokeColor : 'black', highlight : false }); board.fullUpdate(); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox06', { boundingbox : [-6.1, 6.5, 6.1, -6.5], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); xaxis.defaultTicks.ticksFunction = function() { return 2; }; yaxis.defaultTicks.ticksFunction = function() { return 2; }; var f = function(x) { return x*x*x/(1+x*x); } board.create('functiongraph', [f, -6.1, 6.1], { strokeWidth : 2.5, strokeColor : 'black', highlight : false }); board.fullUpdate(); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox07', { boundingbox : [-6.77, 6, 6.77, -6], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); var f = function(x) { return Math.sin(x); } var df = function(x) { return Math.cos(x); } board.create('functiongraph', [f, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'red' }); board.create('functiongraph', [df, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'black' }); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox08', { boundingbox : [-6.77, 6, 6.77, -6], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); var f = function(x) { return Math.cos(x); } var df = function(x) { return Math.sin(x); } board.create('functiongraph', [f, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'blue' }); board.create('functiongraph', [df, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'black' }); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox09', { boundingbox : [-6.77, 6, 6.77, -6], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); var f = function(x) { return Math.tan(x); } var df = function(x) { return 1/Math.pow(Math.cos(x),2); } board.create('functiongraph', [f, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'green' }); board.create('functiongraph', [df, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'black' }); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox10', { boundingbox : [-3.2, 4.5, 4.8, -2.5], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); var f = function(x) { return Math.pow(2*x*x-1, 3); } var df = function(x) { return 6*Math.pow(2*x*x-1, 2); } board.create('functiongraph', [f, 0, 4.8], { strokeWidth : 1.5, strokeColor : 'green' }); board.create('functiongraph', [df, 0, 4.8], { strokeWidth : 1.5, strokeColor : 'black' }); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox11', { boundingbox : [-6.77, 6, 6.77, -6], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); var f = function(x) { return Math.sin(3*x); } var df = function(x) { return 3*Math.cos(x); } board.create('functiongraph', [f, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'red' }); board.create('functiongraph', [df, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'black' }); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox12', { boundingbox : [-6.77, 6, 6.77, -6], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); var f = function(x) { return Math.pow(Math.cos(2*x), 3); } var df = function(x) { return -6*Math.sin(2*x)*Math.pow(Math.cos(2*x), 2); } board.create('functiongraph', [f, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'blue' }); board.create('functiongraph', [df, -6.77, 6.77], { strokeWidth : 1.5, strokeColor : 'black' }); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox13', { boundingbox : [-4.73, 4.2, 4.73, -4.2], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); var f = function(x) { return x*x*x-3*x+1; } var df = function(x) { return 3*x*x-3; } board.create('functiongraph', [f, -3.2, 3.2], { strokeWidth : 1.5, strokeColor : 'blue' }); board.create('functiongraph', [df, -3.2, 3.2], { strokeWidth : 1.5, strokeColor : 'red' }); var p = []; p[0] = board.create('point', [-1, f(-1)]); p[1] = board.create('point', [-1, df(-1)]); p[2] = board.create('point', [1, f(1)]); p[3] = board.create('point', [1, df(1)]); for(var i=0; i < p.length; i++) { p[i].setAttribute({ strokeColor : 'black', size : .5, name : '', fillColor : 'black', fixed : true }); } board.create('segment', [p[0],p[1]], { strokeColor : 'black', dash : 1, highlight : false }); board.create('segment', [p[2],p[3]], { strokeColor : 'black', dash : 1, highlight : false }); board.fullUpdate(); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox14', { boundingbox : [-6.76, 1, 6.76, -11], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); var f = function(x) { return Math.pow(x, 4)/4-2*x*x-7; } board.create('functiongraph', [f, -5.6, 5.6], { strokeWidth : 1.5, strokeColor : 'black' }); var p = []; p[0] = board.create('point', [-2, 0], { }); p[1] = board.create('point', [-2, f(-2)], { }); p[2] = board.create('point', [0, 0], { }); p[3] = board.create('point', [0, f(0)], { }); p[4] = board.create('point', [2, 0], { }); p[5] = board.create('point', [2, f(2)], { }); for(var i=0; i < p.length; i++) { p[i].setAttribute({ visible : false }); } board.create('segment', [p[0],p[1]], { strokeColor : 'red', highlight : false, fixed : true }); board.create('segment', [p[2],p[3]], { strokeColor : 'blue', highlight : false, fixed : true }); board.create('segment', [p[4],p[5]], { strokeColor : 'red', highlight : false, fixed : true }); board.fullUpdate(); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox15', { boundingbox : [-1, 15, 10, -1.5], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); xaxis.defaultTicks.ticksFunction = function() { return 2; }; yaxis.defaultTicks.ticksFunction = function() { return 2; }; var f = function(x) { return (2*x*x+18)/x; } var graph = board.create('functiongraph', [f, -1, 15.9], { strokeColor : 'black', strokeWidth : 2.5, highlight : false }); var p = []; p[0] = board.create('point', [3, 0]); p[1] = board.create('point', [3,f(3)]); for(var i=0; i < p.length; i++) { p[i].setAttribute({ name : '', size : 1, strokeColor : 'black', strokeWidth : .5, fixed : true }); } board.create('segment', [p[0], p[1]], { dash : 1, strokeWidth : 2, strokeColor : 'red', fixed : true, highlight : false }); board.fullUpdate(); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox16', { boundingbox : [-1, 13, 5, -1], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); xaxis.defaultTicks.ticksFunction = function() { return 2; }; yaxis.defaultTicks.ticksFunction = function() { return 2; }; var f = function(x) { return Math.PI*x*x+2/x; } var graph = board.create('functiongraph', [f, 0, 5], { strokeColor : 'black', strokeWidth : 2.5, highlight : false }); var p = []; var a = 1/Math.pow(Math.PI,1/3); p[0] = board.create('point', [a, 0]); p[1] = board.create('point', [a, f(a)]); for(var i=0; i < p.length; i++) { p[i].setAttribute({ name : '', size : 1, strokeColor : 'black', fixed : true }); } board.create('segment', [p[0], p[1]], { dash : 1, strokeWidth : 2, strokeColor : 'red', fixed : true, highlight : false }); board.fullUpdate(); })(); (function() { var board = JXG.JSXGraph.initBoard('jxgbox17', { boundingbox : [-4, 4, 4, -4], axis : false, shownavigation : false, showcopyright : false }); var xaxis = board.create('axis', [[0, 0], [1, 0]], { highlight : false, drawZero : true, ticks : { minorTicks : 0, majorHeight : 9, label : { highlight : false, offset : [-5, -15] } } }); var yaxis = board.create('axis', [[0, 0], [0, 1]], { highlight : false, ticks : { minorTicks : 0, majorHeight : 9, label : { offset : [-15, 0 ], position : 'lrt', highlight : false } } }); xaxis.defaultTicks.ticksFunction = function() { return 1; }; yaxis.defaultTicks.ticksFunction = function() { return 1; }; var s = board.create('slider', [[-3.5, 3.5], [-.5, 3.5], [-10, 0, 10]],{ suffixLabel : ' $c=', postLabel : '$', label : { useMathJax : true, fontSize : 13 }, fillColor : '#31d490', withTicks : false, precision : 2, snapWidth : 1 }); var f = function(x) { return x*x*x-x; } var g = function(x) { return s.Value()*(x*x*x-x); } var graph1 = board.create('functiongraph', [f, -4, 4], { strokeColor : '#4260f5', strokeWidth : 2.5, highlight : false, strokeOpacity : 0.6, highlight : false }); var graph2 = board.create('functiongraph', [g, -4, 4], { strokeColor : '#31d490', strokeWidth : 2.5, highlight : false, strokeOpacity : .8, highlight : false }); var g0 = board.create('glider', [0, 0, xaxis], { name : '$x' + '_' + '0$', size : 4, strokeColor : 'black', strokeWidth : .7, fillColor : '#42f57e', label : { useMathJax : true } }); var g1 = board.create('glider', [0, 0, graph1], { name : '', size : 2, strokeWidth : .7, strokeColor : 'black', fillColor : '#42f57e', fixed : true, highlight : false }); var l1 = board.create('line', [g0, g1], { straightFirst : false, strokeColor : '#42f57e', dash : 1, highlight : false }); var g2 = board.create('glider', [0, 0, graph2], { visible : false }); var t1 = board.create('tangent', [g1], { strokeColor : '#4260f5', strokeWidth : 2.5, strokeOpacity : 0.6, highlight : false }); var t2 = board.create('tangent', [g2], { strokeColor : '#31d490', strokeWidth : 2.5, strokeOpacity : .8, highlight : false }); board.create('text', [-3.5, 2.8, function() { return '$f(x)=\\color{#4260f5}{x^3-x}$'; }], { useMathJax : true, fontSize : 13, strokeColor : 'black', fixed : true, highlight : false }); board.create('text', [-3.5, 2.3, function() { return '$g(x)=c\\color{#31d490}{(x^3-x)}$'; }], { useMathJax : true, fontSize : 13, strokeColor : 'black', fixed : true, highlight : false }); board.create('text', [1.5, -2, function() { return '$f\'(x_{0})=\\color{#4260f5}{' + t1.getSlope().toFixed(3) + '}$'; }], { useMathJax : true, fontSize : 13, strokeColor : 'black', fixed : true, highlight : false }); board.create('text', [1.5, -2.5, function() { return '$g\'(x_{0})=\\color{#31d490}{' + t2.getSlope().toFixed(3) + '}$'; }],{ useMathJax : true, fontSize : 13, strokeColor : 'black', fixed : true, highlight : false }); g0.on('drag', function() { var x = g0.X(); g1.moveTo([x, f(x)]); g2.moveTo([x, g(x)]); board.update(); }); board.fullUpdate(); })(); "; } ], { fontSize : 15 });*/ board.unsuspendUpdate(); } } function addDerivative() { if (JXG.isFunction(f)) { board.create('functiongraph',[JXG.Math.Numerics.D(f), function(){ var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[0,0],board); return c.usrCoords[1]; }, function(){ var c = new JXG.Coords(JXG.COORDS_BY_SCREEN,[board.canvasWidth,0],board); return c.usrCoords[1]; }], { dash : 2, strokeWidth : 2, strokeColor : '#3ac946' }); } } document.getElementById('plot').onclick = plotter; document.getElementById('clear all').onclick = clearAll; document.getElementById('add tangent').onclick = addTangent; document.getElementById('add Derivative').onclick = addDerivative; })();