MS-A0111 - Differential and Integral Calculus 1, Lecture, 13.9.2021-27.10.2021
Kurssiasetusten perusteella kurssi on päättynyt 27.10.2021 Etsi kursseja: MS-A0111
Differential and Integral Calculus
6. Elementary functions
This chapter gives some background to the concept of a function. We also consider some elementary functions from a (possibly) new viewpoint. Many of these should already be familiar from high school mathematics, so in some cases we just list the main properties.
Functions
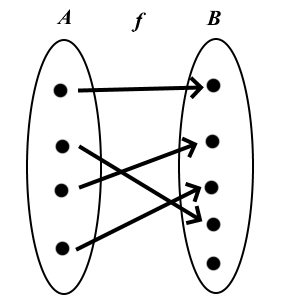
Definition: Function
A function  is a rule that
determines for each element
is a rule that
determines for each element  exactly one element
exactly one element  .
We write
.
We write  .
.
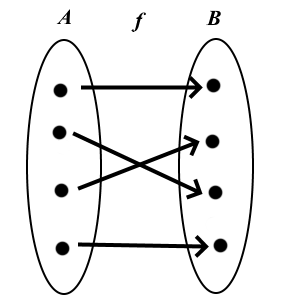
Definition: Domain and codomain
In the above definition of a function  is the domain (of definition) of the function
is the domain (of definition) of the function  and
and  is called the codomain
of
is called the codomain
of  .
.
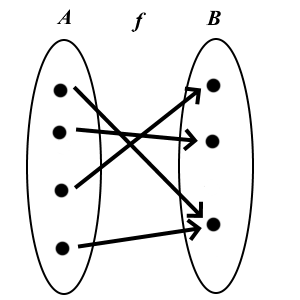
Definition: Image of a function
The image of  is the subset
is the subset
![f[A]= \{ f(a) \mid a\in A\} f[A]= \{ f(a) \mid a\in A\}](https://mycourses.aalto.fi/filter/tex/pix.php/c7a396190ef1775b42655b3bae2aeea4.gif) of
of  . An alternative name for image is range.
. An alternative name for image is range.
For example,  ,
,  , has codomain
, has codomain  ,
but its image is
,
but its image is ![f[\mathbb{R} ] =[0,\infty[ f[\mathbb{R} ] =[0,\infty[](https://mycourses.aalto.fi/filter/tex/pix.php/0c14bcce17985fbb3a35d6def4a9a469.gif) .
.
The function in the previous example can also be defined as
 ,
,  , and then the codomain is the same as the image.
In principle, this modification can always be done, but it is not reasonable
in practice.
, and then the codomain is the same as the image.
In principle, this modification can always be done, but it is not reasonable
in practice.
Inverse functions
Observe: A function becomes surjective if all redundant points of the codomain are left out. A function becomes injective if the domain is reduced so that no value of the function is obtained more than once.
Another way of defining these concepts is based on the number of solutions to an equation:
Definition
Definition: Inverse function
If  is bijective, then it has an inverse
is bijective, then it has an inverse
 , which is uniquely determined by the condition
, which is uniquely determined by the condition

The inverse satisfies  for all
for all  and
and
 for all
for all  .
.
The graph of the inverse is the mirror image of the graph of  with respect to the
line
with respect to the
line  : A point
: A point  lies on the graph of
lies on the graph of 




 the point
the point  lies on the
graph of
lies on the
graph of  . The geometric interpretation of
. The geometric interpretation of  is precisely the
reflection with respect to
is precisely the
reflection with respect to  .
.
If  and
and  is strictly monotone, then
the function
is strictly monotone, then
the function ![f\colon A \to f[A] f\colon A \to f[A]](https://mycourses.aalto.fi/filter/tex/pix.php/c6fc43e8a306502af369ccf4e67dfa13.gif) has an inverse.
has an inverse.
If here  is an interval and
is an interval and  is continuous, then also
is continuous, then also  is
is continuous in the set
is
is continuous in the set ![f[A] f[A]](https://mycourses.aalto.fi/filter/tex/pix.php/e81e3f1f3f2f27271e7259b5b1e92b05.gif) .
.
Theorem: Derivative of the inverse
Let ![f\colon \, ]a,b[\, \to\, ]c,d[ f\colon \, ]a,b[\, \to\, ]c,d[](https://mycourses.aalto.fi/filter/tex/pix.php/d743062611593c099de64ea09a96ce0e.gif) be differentiable and bijective, so that it has an inverse
be differentiable and bijective, so that it has an inverse
![f^{-1}\colon \, ]c,d[\, \to\, ]a,b[ f^{-1}\colon \, ]c,d[\, \to\, ]a,b[](https://mycourses.aalto.fi/filter/tex/pix.php/12920db7181cead890f182a6b37094a0.gif) . As the graphs
. As the graphs  and
and  are mirror images of each other, it seems geometrically obvious that also
are mirror images of each other, it seems geometrically obvious that also  is differentiable, and we actually have
is differentiable, and we actually have
 if
if  .
.
Transcendental functions
Trigonometric functions
Unit of measurement of an angle = rad: the arclength of the arc on the unit circle, that corresponds to the angle.
The functions
 are defined in terms of the unit circle so that
are defined in terms of the unit circle so that
 ,
, ![x\in [0,2\pi] x\in [0,2\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/45279ec769d88b24314782eea30c7f1e.gif) , is the point on the unit circle corresponding to the
angle
, is the point on the unit circle corresponding to the
angle  , measured counterclockwise from the point
, measured counterclockwise from the point  .
.


Proof: Pythagorean Theorem.
Addition formulas:
Basic properties (from the unit circle!)
Proof: Geometrically, or more easily with vectors and matrices.
Example
It follows that the functions
 and
and  satisfy the
differential equation
satisfy the
differential equation
 that models harmonic oscillation. Here
that models harmonic oscillation. Here  is the time variable
and the constant
is the time variable
and the constant  is the angular frequency of the oscillation.
We will see later that all the solutions of this differential equation
are of the form
is the angular frequency of the oscillation.
We will see later that all the solutions of this differential equation
are of the form
 with
with  constants. They will be uniquely determined if we know
the initial location
constants. They will be uniquely determined if we know
the initial location  and the initial velocity
and the initial velocity  . All solutions
are periodic and their period is
. All solutions
are periodic and their period is  .
.
Arcus functions
The trigonometric functions have inverses if their domain and codomains are chosen in a suitable way.
Here we will only prove the first result (1). By differentiating
both sides of the equation  for
for  :
:



The last row follows also directly from the formula for the derivative of an inverse.
Example
Example
Derive the addition formula for tan, and show that

Solutions: Voluntary exercises. The first can be deduced by looking at
a rectangular triangle with the length of the hypotenuse equal to 1
and one leg of length  .
.
Introduction: Radioactive decay
Let  model the number of radioactive nuclei at time
model the number of radioactive nuclei at time  .
During a short time interval
.
During a short time interval  the number of decaying nuclei is (approximately) directly proportional to
the length of the interval, and also to the number of nuclei at time
the number of decaying nuclei is (approximately) directly proportional to
the length of the interval, and also to the number of nuclei at time  :
:
 The constant
The constant  depends on the substance and is called the decay constant.
From this we obtain
depends on the substance and is called the decay constant.
From this we obtain
 and in the limit as
and in the limit as  we end up with the differential equation
we end up with the differential equation  .
.
Exponential function
Definition: Exponential function
The Exponential function exp:
 This definition (using the series expansion) is based on the conditions
This definition (using the series expansion) is based on the conditions
 and
and  , which imply
that
, which imply
that  for all
for all  ,
so the Maclaurin series is the one above.
,
so the Maclaurin series is the one above.
The connections between different expressions are surprisingly tedious to prove, and we omit the details here. The main steps include the following:
From here on we write  . Properties:
. Properties:
 .
.
Differential equation 
Theorem
Let  be a constant. All solutions
be a constant. All solutions  of the ordinary differenial equation (ODE)
of the ordinary differenial equation (ODE)
 are of the form
are of the form  , where
, where  is a constant. If we know
the value of
is a constant. If we know
the value of  at some point
at some point  , then the constant
, then the constant
 will be uniquely determined.
will be uniquely determined.
Euler's formula
Definition: Complex numbers
Imaginary unit  : a strange creature satisfying
: a strange creature satisfying  . The complex numbers
are of the form
. The complex numbers
are of the form  , where
, where  . We will return to these later.
. We will return to these later.
Theorem: Euler's formula
If we substitute  as a variable in the expontential fuction, and
collect real terms separately, we obtain Euler's formula
as a variable in the expontential fuction, and
collect real terms separately, we obtain Euler's formula

 in the definition of the exponential function and write the series as the sum
of its even (
in the definition of the exponential function and write the series as the sum
of its even ( ) and odd
) and odd  parts. Note that
parts. Note that  and remember the Taylor series of the trigonometric
functions.
and remember the Taylor series of the trigonometric
functions.
As a special case we have Euler's identity  .
It connects the most important numbers
.
It connects the most important numbers  ,
,  ,
,  ,
,  ja
ja  and the
three basic operations sum, multiplication, and power.
and the
three basic operations sum, multiplication, and power.
Logarithms
Hyperbolic functions
Definition: Hyperbolic functions
Hyperbolic sine sinus hyperbolicus  ,
hyperbolic cosine cosinus hyperbolicus
,
hyperbolic cosine cosinus hyperbolicus  and hyperbolic tangent
and hyperbolic tangent
 are defined as
are defined as


![\tanh \colon \mathbb{R}\to \ ]-1,1[, \ \tanh x =\frac{\sinh x}{\cosh x} \tanh \colon \mathbb{R}\to \ ]-1,1[, \ \tanh x =\frac{\sinh x}{\cosh x}](https://mycourses.aalto.fi/filter/tex/pix.php/2ac4198587d98a4f7dd3df05218f66f7.gif)
Properties:  ; all trigonometric have their hyperbolic counterparts,
which follow from the properties
; all trigonometric have their hyperbolic counterparts,
which follow from the properties  ,
,  .
In these formulas, the sign of
.
In these formulas, the sign of  will change, but the other signs remain the same.
will change, but the other signs remain the same.
Hyperbolic inverse functions: the so-called area functions;
area and the shortening ar refer to a certain geometrical area
related to the hyperbola  :
:


 ',
radius : .4,
label : { useMathJax : true, strokeColor : 'black', offset : [0, .5] }
});
var info = board.create('text', [-1.2, -1.25, function() {
return '
',
radius : .4,
label : { useMathJax : true, strokeColor : 'black', offset : [0, .5] }
});
var info = board.create('text', [-1.2, -1.25, function() {
return ' ';
}], {
useMathJax : true,
fixed : true
});
board.fullUpdate();
})();
';
}], {
useMathJax : true,
fixed : true
});
board.fullUpdate();
})();







![f[A]=B f[A]=B](https://mycourses.aalto.fi/filter/tex/pix.php/c0dfc65c448fbf8cef4d8969eab57661.gif)

























![\sin \colon [-\pi/2,\pi/2]\to [-1,1]
\sin \colon [-\pi/2,\pi/2]\to [-1,1]](https://mycourses.aalto.fi/filter/tex/pix.php/8516ac159a27828b8807ae8346208684.gif)
![\cos \colon [0,\pi] \to [-1,1]
\cos \colon [0,\pi] \to [-1,1]](https://mycourses.aalto.fi/filter/tex/pix.php/7b6724fb6d58f64ba500defadc44773d.gif)
![\tan \colon ]-\pi/2,\pi/2[\, \to \mathbb{R}
\tan \colon ]-\pi/2,\pi/2[\, \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/04f0656b3b1805879518b5a4d600ae97.gif)
![\arctan \colon \mathbb{R}\to \ ]-\pi/2,\pi/2[, \arctan \colon \mathbb{R}\to \ ]-\pi/2,\pi/2[,](https://mycourses.aalto.fi/filter/tex/pix.php/5a0cfc94ec76b4bb98759ea997a6814e.gif)
![\arcsin \colon [-1,1]\to [-\pi/2,\pi/2], \arcsin \colon [-1,1]\to [-\pi/2,\pi/2],](https://mycourses.aalto.fi/filter/tex/pix.php/c4d09554c2fd5fc1cbf2d81a599c1b95.gif)
![\arccos \colon [-1,1]\to [0,\pi] \arccos \colon [-1,1]\to [0,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/ae1f9e9c619a7daceef40e2227521839.gif)
![x = \tan \alpha \Leftrightarrow \alpha = \arctan x \ \ \text{for } \alpha \in \ ]-\pi/2,\pi/2[ x = \tan \alpha \Leftrightarrow \alpha = \arctan x \ \ \text{for } \alpha \in \ ]-\pi/2,\pi/2[](https://mycourses.aalto.fi/filter/tex/pix.php/1e8adfc9de7373123d3e37d24295583b.gif)
![x = \sin \alpha \Leftrightarrow \alpha = \arcsin x \ \ \text{for } \alpha \in \, [-\pi/2,\pi/2] x = \sin \alpha \Leftrightarrow \alpha = \arcsin x \ \ \text{for } \alpha \in \, [-\pi/2,\pi/2]](https://mycourses.aalto.fi/filter/tex/pix.php/e0f134a17e198c541c553b3c2e9305f0.gif)
![x = \cos \alpha \Leftrightarrow \alpha = \arccos x \ \ \text{for } \alpha \in \, [0,\pi] x = \cos \alpha \Leftrightarrow \alpha = \arccos x \ \ \text{for } \alpha \in \, [0,\pi]](https://mycourses.aalto.fi/filter/tex/pix.php/eab3cb1a5193c48cde03e2046ec37027.gif)

















![\exp\colon\mathbb{R}\to\, ]0,\infty[ \exp\colon\mathbb{R}\to\, ]0,\infty[](https://mycourses.aalto.fi/filter/tex/pix.php/463736f26c065deb116e8539cc1e1c90.gif)

















![\ln\colon \ ]0,\infty[ \ \to \mathbb{R}
\ln\colon \ ]0,\infty[ \ \to \mathbb{R}](https://mycourses.aalto.fi/filter/tex/pix.php/a57877163d9051a40ddff6a55fb8ea50.gif)



























