7. Pinta-ala

Pinta-ala tasossa

Tarkastellaan umpinaisen ja itseään leikkaamattoman tasokäyrän raamien alueiden pinta-alaa. Pinta-alan yleinen käsite on teoreettisesti paljon hankalampi, mistä antaa viitteen luvun lopussa oleva huomautus.

Tasojoukon pinta-ala määritellään palauttamalla se yksinkertaisempien joukkojen pinta-aloihin. Erityisesti täytyy huomata, ettei pinta-alaa voi "laskea", ellei "pinta-alan" käsitettä ole ensin määritelty (vaikka koulumatematiikassa näin usein tehdäänkin).

Lähtökohta

Suorakulmion pinta-ala
Suorakulmion pinta-ala on kanta \(\times\) korkeus: \[A=ab.\]

rectangle
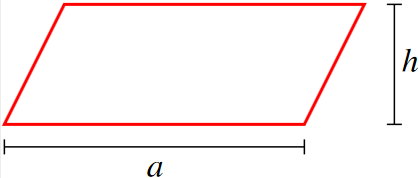
Määritelmä: Suunnikkaan pinta-ala

Suunnikkaan pinta-ala on kanta \(\times\) korkeus: \[ A=ah. \]


parallelogram
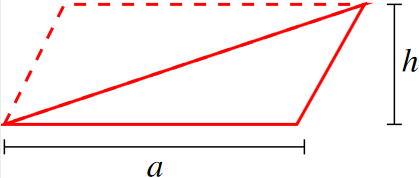
Määritelmä: Kolmion pinta-ala

Kolmion pinta-ala on (määritelmän mukaan) \[ A=\frac{1}{2}ah. \]


triangle

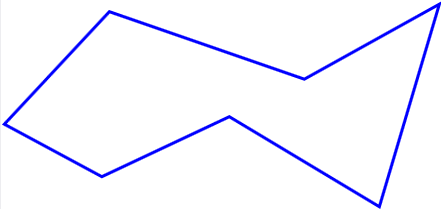
Monikulmio

(Yksinkertainen) monikulmio on tasojoukko, jota rajaa äärellisestä määrästä peräkkäisiä janoja koostuva suljettu käyrä. Vain peräkkäiset janat saavat leikata toisiaan yhteisessä päätepisteessä.

polygon
Määritelmä: Monikulmion pinta-ala

Monikulmion pinta-ala määritellään jakamalla se äärelliseen määrään kolmioita (monikulmion kolmiointi) ja laskemalla kolmioiden pinta-alat yhteen.


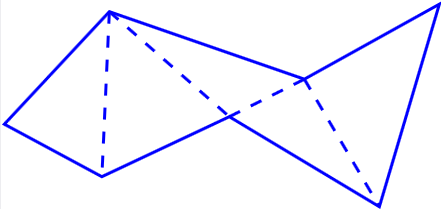
triangulation
Lause.

Kolmioiden pinta-alojen summaf  ei riipu monikulmion kolmioinnin valinnasta.


Yleinen tapaus

Tasojoukolle \(\color{red} D\), jota rajaa umpinainen itseään leikkaamaton käyrä, voidaan muodostaa sisämonikulmioita \(\color{blue}P_i\) ja ulkomonikulmioita \(P_o\): \(\color{blue}P_i\color{black} \subset \color{red}D\color{black}\subset P_o\).

Rajoitetulla tasojoukolla \(D\) on pinta-ala, jos jokaista \(\varepsilon >0\) vastaa sisämonikulmio \(P_i\) ja ulkomonikulmio \(P_o\), joiden pinta-alat poikkeavat toisistaan vähemmän kuin \(\varepsilon\): \[ A(P_o)-A(P_i)<\varepsilon. \] Tästä seuraa, että kaikkien lukujen \(A(P_i)\) ja kaikkien lukujen \(A(P_o)\) välissä on yksikäsitteinen luku \(A(D)\), joka on määritelmän mukaan joukon \(D\) pinta-ala.

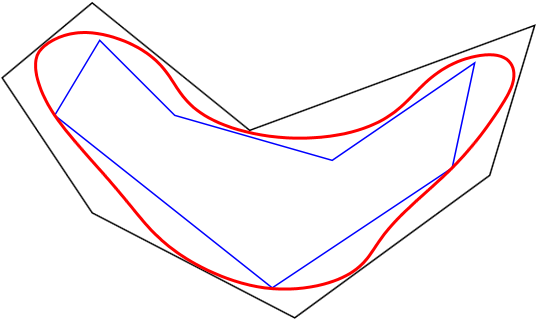
Inner and outer polygons

Yllätys: Se, että joukkoa \(D\) rajoittaa umpinainen (itseään leikkaamaton) käyrä, ei takaa, että joukon pinta-ala on määritelty: Reunakäyrä voi olla niin "mutkitteleva", että sillä on positiivinen "pinta-ala". Ensimmäisen esimerkin konstruoi [W.F. Osgood, 1903]:

Wikipedia: Osgood curve

Esimerkki

Johda \(R\)-säteisen ympyrän pinta-alan kaava \(A=\pi R^2\) valitsemalla sisä- ja ulkomonikulmioiksi säännöllisiä \(n\)-kulmioita, ja ottamalla lopuksi raja-arvo \(n\to\infty\).

Ratkaisu: vapaaehtoinen lisätehtävä, jossa tarvitaan raja-arvoa \[\lim_{x\to 0}\frac{\sin x}{x} = 1.\] Vihje: Osoita, että säännöllisten sisä- ja ulkomonikulmioiden pinta-alat ovat \[ \pi R^2\frac{\sin (2\pi/n)}{2\pi/n} \ \text{ ja }\ \pi R^2\frac{\tan \pi/n}{\pi/n}.\]