MS-A0101 - Differentiaali- ja integraalilaskenta 1 (TFM), Luento-opetus, 13.9.2021-27.10.2021
This course space end date is set to 27.10.2021 Search Courses: MS-A0101
Differentiaali- ja integraalilaskenta
Englanninkielisen MOOC-kurssin luentomateriaali, joka perustuu tämän kurssin luentoihin. Mukana on interaktiivisia JSXGraph-kuvia, joita ei ole suomenkielisissä luentokalvoissa. Tässä vaiheessa vain luvut 1, 2, 7 ja 9 ovat suomeksi.
1. Jonot
Sisältö
- Peruskäsitteet
- Tärkeitä jonoja
- Suppeneminen ja raja-arvo
Jonot
Tämä luku sisältää tärkeimmät jonoihin liittyvät käsitteet. Käsittelemme käytännössä vain reaalilukujonohin liittyviä asioita.
Määritelmä: Jono
Olkoon \(M\) epätyhjä joukko. Jono on funktio
\[f:\mathbb{N}\rightarrow M.\]
Usein käytetään nimitystä jono joukossa \(M\).Huom. Koska \(\mathbb{N}\) on järjestetty joukko, niin myös jonon termeillä \( f(n)\) on vastaava järjestys. Sen sijaan joukon alkioilla ei yleisessä tapauksessa
ole määrättyä järjestystä.
Määritelmä: Jonon termit ja indeksit
Jonoille voidaan käyttää myös merkintöjä
\((a_{1}, a_{2}, a_{3}, \ldots) = (a_{n})_{n\in\mathbb{N}} = (a_{n})_{n=1}^{\infty} = (a_{n})_{n}\)
muodon \(f(n)\) sijaan. Luvut \(a_{1},a_{2},a_{3},\ldots\in M\) ovat jonon termejä.
Funktion \[\begin{aligned} f:\mathbb{N} \rightarrow & M \\ n \mapsto & a_{n}\end{aligned}\] perusteella jokaiseen jonon termiin liittyy yksikäsitteinen lukua \(n\in\mathbb{N}\) to each term. Se merkitään alaindeksinä ja sitä kutsutaan vastaavan jonon termin indeksiksi; jokainen jonon termi voidaan siis tunnistaa sen indeksin avulla.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | \(\ldots\) |
|---|---|---|---|---|---|---|---|---|---|---|
| \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | ||
| \(a_{n}\) | \(a_{1}\) | \(a_{2}\) | \(a_{3}\) | \(a_{4}\) | \(a_{5}\) | \(a_{6}\) | \(a_{7}\) | \(a_{8}\) | \(a_{9}\) | \(\ldots\) |
Esimerkkejä
Esimerkki 1: Luonnollisten lukujen jono
Jono \((a_{n})_{n}\), joka on määritelty kaavalla \(a_{n}:=n,\,n\in \mathbb{N}\) on nimeltään luonnollisten lukujen jono. Sen ensimmäiset termit ovat:
\[a_1=1,\, a_2=2,\, a_3=3, \ldots\]
![]()
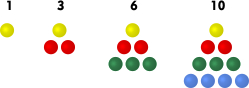
Esimerkki 2: Kolmiolukujen jono
Kolmioluvut saavat nimensä seuraavasta geometrisesta periaatteesta: Asetetaan sopiva määrä kolikoita niin, että syntyy yhä suurempia tasasivuisia kolmioita:
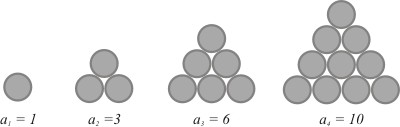
Ensimmäisen kolikon alle lisätään kaksi kolikkoa, jolloin toisessa vaiheessa saadaan \(a_2=3\) kolikkoa. Seuraavaksi tämän kolmion alle lisätään kolme uutta kolikkoa, joita on nyt yhteensä \(a_3=6\).
Etenemällä samaan tapaan huomataan, että esimerkiksi 10. kolmioluku saadaan laskemalla yhteen 10 ensimmäistä luonnollista lukua:
\[a_{10} = 1+2+3+\ldots+9+10.\] Yleinen kaava kolmiolukujonon termeille on \(a_{n} = 1+2+3+\ldots+(n-1)+n\). Kolmioluvuille käytetään yleensä merkintää \(T_n\) (T = 'Triangle').
Tämä motivoi seuraavaan määritelmään:
Määritelmä: Summajono
Olkoon \((a_n)_n, a_n: \mathbb{N}\to M\) jono joukossa \( M\), jossa on määritelty yhteenlasku. Merkitään \[a_1 + a_2 + a_3 + \ldots + a_{n-1} + a_n =: \sum_{k=1}^n a_k.\] Symboli \(\sum\) on kreikkalainen kirjain sigma. Summausindeksi \(k\) kasvaa alkuarvosta 1 loppuarvoon \(n\).
Summajono saadaan siis alkuperäisestä jonosta laskemalla alkupään termejä yhteen aina yksi termi eteenpäin. Varsinkin sarjojen kohdalla käytetään nimeä osasummajono.
Kolmiolukujen yleinen kaava voidaan siis kirjoittaa muodossa
\[T_n = \sum_{k=1}^n k\] ja kyseessä on luonnollisten lukujen jonon summajono.
Esimerkki 3: Neliölukujen jono
Neliölukujen jono \((q_n)_n\) määritellään kaavalla \(q_n=n^2\). Tämän jonon termejä voidaan havainnollistaa asettelemalla kolikoita neliön muotoon.
Yksi mielenkiintoinen havainto on se, että kahden peräkkäisen kolmioluvun summa on aina neliöluku. Esimerkiksi \(3+1=4\) ja \(6+3=9\). Yleisesti määritelmiä käyttämällä
voidaan osoittaa, että
\[q_n=T_n + T_{n-1}.\]

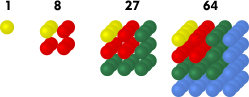
Esimerkki 4: Kuutiolukujen jono
Vastaavasti kuutiolukujen jono määritellään kaavalla \[a_n := n^3.\] Jonon ensimmäiset termit ovat silloin \((1,8,27,64,125,\ldots)\).
Esimerkki 5.
Olkoon \((q_n)_n\) with \(q_n := n^2\) neliölukujen jono \[\begin{aligned}(1,4,9,16,25,36,49,64,81,100 \ldots)\end{aligned}\] ja määritellään funktio \(\varphi(n) = 2n\). Jonosta \((q_{2n})_n\) saadaan \[\begin{aligned}(q_{2n})_n &= (q_2,q_4,q_6,q_8,q_{10},\ldots) \\ &= (4,16,36,64,100,\ldots).\end{aligned}\]
Määritelmä: Erotusjono (differenssijono)
Jonon \((a_{n})_{n}=a_{1},\, a_{2},\, a_{3},\ldots,\, a_{n},\ldots\) termeistä voidaan myös muodostaa peräkkäisten termien erotuksia: \[(a_{n+1}-a_{n})_{n}:=a_{2}-a_{1}, a_{3}-a_{2},\dots\] on nimeltään alkuperäisen jonon \((a_{n})_{n}\) ensimmäinen differenssijono.
Ensimmäisen differenssijonon ensimmäinen differenssijono on alkuperäisen jonon toinen differenssijono. sequence. Vastaavalla tavalla määritellään jonon \(n.\) differenssijono.
Esimerkki 6.
Tarkastellaan jonoa \((a_n)_n\), jossa \(a_n := \frac{n^2+n}{2}\), eli \[\begin{aligned}(a_n)_n &= (1,3,6,10,15,21,28,36,\ldots)\end{aligned}\] Olkoon \((b_n)_n\) sen 1. differenssijono. Silloin \[\begin{aligned}(b_n)_n &= (a_2-a_1, a_3-a_2, a_4-a_3,\ldots) \\ &= (2,3,4,5,6,7,8,9,\ldots)\end{aligned}\] Termin \((b_n)_n\) yleinen muoto on \[\begin{aligned}b_n &= a_{n+1}-a_{n} \\ &= \frac{(n+1)^2+(n+1)}{2} - \frac{n^2+n)}{2} \\ &= \frac{(n+1)^2+(n+1)-n^2 - n }{2} \\ &= \frac{(n^2+2n+1)+1-n^2}{2} \\ &= \frac{2n+2}{2} \\ &= n + 1.\end{aligned}\]
Eräitä tärkeitä jonoja
Eräät jonot ovat keskeisiä monille matemaattisille malleille ja niiden käytännön sovelluksille muilla aloilla kuten luonnontieteissä ja taloustieteissä.) Seuraavassa tarkastellaan kolme tällaista jonoa: aritmeettinen jono, geometrinen jono ja Fibonaccin lukujono.
Aritmeettinen jono
Aritmeettinen jono voidaan määritellä monella eri tavalla:Määritelmä A: Aritmeettinen jono
Jono \((a_{n})_{n}\) on aritmeettinen, jos sen peräkkäisten termien erotus \(d \in \mathbb{R}\) on vakio, t.s. \[a_{n+1}-a_{n}=d \text{ ja } d=vakio.\]
Huomautus: Aritmeettisen jonon eksplisiittinen kaava seuraa suoraan määritelmästä A: \[a_{n}=a_{1}+(n-1)\cdot d.\] Aritmeettisen jonon \(n.\) termi voidaan laskea myös palautuskaavan (eli rekursiokaavan) avulla: \[a_{n+1}=a_n + d.\]
Määritelmä B: Aritmeettinen jono
Jono \((a_{n})_{n}\) on aritmeettinen jono, jos sen ensimmäinen differenssijono on vakiojono.
Tämä määritelmä selventää myös aritmeettisen jonon nimen: Kolmen peräkkäisen termin keskimmäinen luku on kahden muun termin aritmeettinen keskiarvo; esimerkiksi
\[a_2 = \frac{a_1+a_3}{2}.\]
Esimerkki 1.
Luonnollisten lukujen jono \[(a_n)_n = (1,2,3,4,5,6,7,8,9,\ldots)\] on aritmeettinen, koska peräkkäisten termien erotus on \(d=1\).
Geometrinen jono
Myös geometrisella jonolla on useita erilaisia määritelmiä:
Määritelmä: Geometrinen jono
Jono \((a_{n})_{n}\) on geometrinen, jos kahden präkkäisen termin suhde on aina vakio \(q\in\mathbb{R}\), t.s. \[\frac{a_{n+1}}{a_{n}}=q \text{ kaikille } n\in\mathbb{N}.\]
Huomautus. Palautuskaava \(a_{n+1} = q\cdot a_n \) geometrisen jonon termeille ja myös eksplisiittinen lauseke \[a_n=a_1\cdot q^{n-1}\] seuraavat suoraan määritelmästä.
Myös tässä jonon nimityksellä on looginen tausta: Kolmen peräkkäisen termin keskimmäinen luku on aina kahden muun termin geometrinen keskiarvo; esimerkiksi \[a_2 = \sqrt{a_1\cdot a_3}.\]
Esimerkki 2.
Olkoon \(a\in\mathbf{R}\) ja \(q\neq 0\). Jono \((a_n)_n\), jolle \(a_n := aq^{n-1}\), eli \[\left( a_1, a_2, a_3, a_4,\ldots \right) = \left( a, aq, aq^2, aq^3,\ldots \right),\] on geometrinen jono. Jos \(a> 0\) ja \(q\geq1\), niin jono on aidosti kasvava. Jos \(a>0\) ja \(q<1\), niin se on aidosti vähenevä. Jonon alkioiden muodostama joukko \({a,aq,aq^2, aq^3}\) on äärellinen, jos \(q=1\) (jolloin sen ainoa alkio on \(a\)), muuten tämä joukko on ääretön.
Fibonaccin jono
Fibonaccin lukujono on kuuluisa sen biologisten sovellusten vuoksi. Se esiintyy mm.eliöiden populaation kasvun yhteydessä ja kasvien rakenteessa. Palautuskaavaan perustuva määritelmä on seuraava:
Määritelmä: Fibonaccin jono
Olkoon \(a_0 = a_1 = 1\) ja \[a_n := a_{n-2}+a_{n-1},\] kun \(n\geq2\). Jono \((a_n)_n\) on Fibonaccin lukujono. Jonon termit ovat Fibonaccin lukuja.
Jonon nimen takana on italialainen Leonardo Pisano (1200-luvulla), latinalaiselta nimeltään Filius Bonacci. Hän tutki kaniparien lisääntymistä idealisoidussa tilanteessa, jossa kanit eivät kuole ja kaikki vanhat sekä uudet parit lisääntyvät säännöllisin väliajoin. Näin hän päätyi jonoon \[(1,1,2,3,5,8,13,21,34,55,\ldots).\]
Esimerkki 3.
Auringonkukan kukat muodostuvat kahdesta spiraalista, jotka aukeavat keskeltä vastakkaisiin suuntiin: 55 spiraalia myötäpäivään ja 34 vastapäivään.
Myös ananashedelmän pinta käyttäytyy samalla tavalla. Siinä on 21 spiraalia yhteen suuntaan ja 34 vastakkaiseen. Myös joissakin kaktuksissa ja havupuiden kävyissä on samanlaisia rakenteita.

Suppeneminen, hajaantuminen ja raja-arvo
Tässä luvussa käsitellään jonon suppenemista. Aloitamme nollajonon käsitteestä ja siirrymme sen avulla yleiseen suppenemisen käsitteeseen.
Huomautus: Itseisarvo joukossa \(\mathbb{R}\)
Itseisarvofunktio \(x \mapsto |x|\) on keskeisessä asemassa jonojen suppenemisen tutkimisessa. Seuraavassa käydään läpi sen tärkeimmät ominaisuudet:
Määritelmä: Itseisarvo
Reaaliluvun \(x\in\mathbb{R}\) itseisarvo \(|x|\) on \[\begin{aligned}|x|:=\begin{cases}x, & \text{jos }x\geq0,\\ -x, & \text{jos }x<0.\end{cases}\end{aligned}\]
Itseisarvofunktion kuvaaja
Lause: Itseisarvon laskusääntöjä
Kaikille reaaliluvuille \(x,y\in\mathbb{R}\) pätee:
-
\(|x|\geq0,\)
-
\(|x|=0\) täsmälleen silloin, kun \(x=0.\)
-
\(|x\cdot y|=|x|\cdot|y|\) (multiplikatiivisuus)
-
\(|x+y|\leq|x|+|y|\) (kolmioepäyhtälö)
Kohdat 1.-3. Results follow directly from the definition and by dividing it up into separate cases of the different signs of \(x\) and \(y\)
Kohta 4. Tämä kohta voidaan todistaa neliöön korottamalla tai tutkimalla kaikki eri vaihtoehdot kuten alla.
Tapaus 1.
Olkoot \(x,y \geq 0\). Silloin \[\begin{aligned}|x+y|=x+y=|x|+|y|\end{aligned}\] ja kaava pätee.
Tapaus 2.Olkoot seuraavaksi \(x,y < 0\). Silloin \[\begin{aligned}|x+y|=-(x+y)=(-x)+ (-y)=|x|+|y|.\end{aligned}\]
Tapaus 3.Tutkitaan lopuksi tapaus \(x\geq 0\) and \(y<0\), joka jakaantuu kahteen alakohtaan:
-
Jos \(x \geq -y\), niin \(x+y\geq 0\) ja siten \(|x+y|=x+y\) määritelmän perusteella. Koska \(y<0\), niin \(y<-y\) ja sen vuoksi \(x+y < x-y\). Siis \[\begin{aligned}|x+y| = x+y < x-y = |x|+|y|.\end{aligned}\]
-
Jos \(x < -y\), niin \(x+y<0\), ja tällöin \(|x+y|=-(x+y)=-x-y\). Koska \(x\geq0\), niin \(-x < x\) ja siten \(-x-y\leq x-y\). Siispä \[\begin{aligned}|x+y| = -x-y \leq x-y = |x|+|y|.\end{aligned}\]
Jos \(x<0\) ja \(y\geq0\), niin väite seuraa samalla periaatteella kuin tapauksessa 3, kun vaihdetaan keskenään \(x\) ja \(y\).
\(\square\)
Nollajono
Määritelmä: Nollajono
Jono \((a_{n})_{n}\) on nollajono, jos jokaista \(\varepsilon>0,\) vastaa sellainen indeksi \(n_{0}\in\mathbb{N}\), että \[|a_{n}| < \varepsilon\] kaikille \(n\geq n_{0},\, n\in\mathbb{N}\). Tällöin sanotaan, että jono suppenee kohti nollaa.
Intuitiivisesti: Nollajonon termit menevät mielivaltaisen lähelle nollaa, kun jonossa mennään riittävän pitkälle.
Esimerkki 1.
Jono \((a_n)_n\), joka on määritelty kaavalla \(a_{n}:=\frac{1}{n}\), eli \[\left(a_{1},a_{2},a_{3},a_{4},\ldots\right):=\left(\frac{1}{1},\frac{1}{2},\frac{1}{3},\frac{1}{4},\ldots\right)\] on nimeltään harmoninen jono. Jonon termit ovat positiivisia kaikilla \(n\in\mathbb{N}\), mutta indeksin \(n\) kasvaessa jonon termit pienenevät yhä lähemmäksi
nollaa.
Jos esimerkiksi \(\varepsilon := \frac{1}{5000}\), niin valinnalla \(n_0 = 5001\) pätee \(a_n<\frac{1}{5000}=\varepsilon\) aina, kun \(n\geq n_0\).
Harmoninen jono suppenee kohti nollaa
Esimerkki 2.
Tarkastellaan jonoa \[(a_n)_n \text{ jossa } a_n:=\frac{1}{\sqrt{n}}.\] Olkoon \(\varepsilon := \frac{1}{1000}\). Tällöin valinnalla \(n_0=1000001\) kaikille termeille \(a_n\), joissa \(n\geq n_0\), pätee \(a_n < \frac{1}{1000}=\varepsilon\).
Note. Tutkittaessa nollajono-ominaisuutta täytyy tutkia mielivaltaista lukua \(\varepsilon \in \mathbb{R}\), jolle \(\varepsilon > 0\). Sen jälkeen yritetään valita sellainen indeksi \(n_0\), josta alkaen jokainen \(|a_n|\) on pienempi kuin \(\varepsilon\).
Esimerkki 3.
Tarkastellaan jonoa \((a_n)_n\), jossa \[a_n := \left( -1 \right)^n \cdot \frac{1}{n^2}.\]
Kerrointen \((-1)^n\) vuoksi jonon kaksi peräkkäistä termiä ovat aina erimerkkisiä; tällaista jonoa kutsutaan yleisemmin vuorottelevaksi jonoksi.
Osoitetaan, että kyseessä on nollajono. Määritelmän mukaan jokaista \(\varepsilon > 0\) täytyy vastata sellainen \(n_0 \in \mathbb{N}\), että epäyhtälö \[|a_n|< \varepsilon\] pätee kaikille niille termeille \(a_n\), joissa \(n\geq n_0\).
Olkoon siis \(\varepsilon > 0\) mielivaltainen. Koska epäyhtälön \( |a_n|< \varepsilon\) täytyy olla voimassa kaikille \(\varepsilon>0\), indeksin \(n_0\) täytyy riippua luvusta \(\varepsilon\). Tarkemmin: Epäyhtälön \[|a_{n_0}|=\left| \frac{1}{{n_0}^2} \right|= \frac{1}{{n_0}^2}<\varepsilon\] täytyy toteutua indeksillä \(n_0\). Ratkaistaan \(n_0\):
\[n_0 > \frac{1}{\sqrt{\varepsilon}}.\]. Mikä tahansa tämän ehdon toteuttava indeksi \(n_0\) kelpaa valinnaksi, kun \(\varepsilon > 0\) on alussa kiinnitetty.
Hajaantuvia esimerkkejä
Seuraavat kaavat eivät johda nollajonoon:
-
\(a_n = (-1)^n\)
-
\(a_n = (-1)^n \cdot n\)
Lause: Nollajonojen ominaisuuksia
Olkoot \((a_n)_n\) ja \((b_n)_n\) jonoja. Silloin pätee:
-
Jos \((a_n)_n\) on nollajono ja joko \(b_n = a_n\) tai \(b_n = -a_n\) kaikilla \(n\in\mathbb{N}\), niin \((b_n)_n\) on myös nollajono.
-
Jos \((a_n)_n\) on nollajono ja \(-a_n\leq b_n \leq a_n\) kaikilla \(n\in\mathbb{N}\), niin \((b_n)_n\) on myös nollajono.
-
Jos \((a_n)_n\) on nollajono, niin \((c\cdot a_n)_n\), \(c \in \mathbb{R}\), on myös nollajono.
-
Jos \((a_n)_n\) ja \((b_n)_n\) ovat nollajonoja, niin \((a_n + b_n)_n\) on myös nollajono.
Parts 1 and 2. If \((a_n)_n\) is a zero sequence, then according to the definition there is an index \(n_0 \in \mathbb{N}\), such that \(|a_n|<\varepsilon\) for every \(n\geq n_0\) and an arbitrary \(\varepsilon\in\mathbb{R}\). But then we have \(|b_n|\leq|a_n|<\varepsilon\); this proves parts 1 and 2 are correct.
Part 3. If \(c=0\), then the result is trivial. Let \(c\neq0\) and choose \(\varepsilon > 0\) such that \[\begin{aligned}|a_n|<\frac{\varepsilon}{|c|}\end{aligned}\] for all \(n\geq n_0\). Rearranging we get: \[\begin{aligned} |c|\cdot|a_n|=|c\cdot a_n|<\varepsilon\end{aligned}\]
Part 4.
Because \((a_n)_n\) is a zero sequence, by the definition we have \(|a_n|<\frac{\varepsilon}{2}\) for all \(n\geq n_0\). Analogously, for the zero sequence \((b_n)_n\) there is a \(m_0 \in \mathbb{N}\) with \(|b_n|<\frac{\varepsilon}{2}\) for all \(n\geq m_0\).
Then for all \(n > \max(n_0,m_0)\) it follows (using the triangle inequality) that: \[\begin{aligned}|a_n + b_n|\leq|a_n|+|b_n|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon\end{aligned}\]
\(\square\)
Suppeneminen ja hajaantuminen
Nollajonoja voidaan käyttää tutkimaan jonojen suppenemista yleisemmin:
Määritelmä: Suppeneminen ja hajaantuminen
Jono \((a_{n})_{n}\) suppenee kohti raja-arvoa \(a\in\mathbb{R}\), jos jokaista \(\varepsilon>0\) vastaa sellainen \(n_{0}\), että \[|a_{n}-a| \lt \varepsilon \text{ kaikille niille }n\in\mathbb{N}_{0},\text{ joille }n\geq n_{0}.\]
Tämän kanssa on yhtäpitävää:
Jono \((a_{n})_{n}\) suppenee kohti raja-arvoa \(a\in\mathbb{R}\), jos \((a_{n}-a)_{n}\) on nollajono.
Esimerkki 4.
Tarkastellaan jonoa \((a_n)_n\), jossa \[a_n=\frac{2n^2+1}{n^2+1}.\] Laskemalla jonon termejä suurilla \(n\), huomataan, että ilmeisesti \( a_n\to 2\), kun \(n \to \infty\), joten jonon raja-arvo voisi olla \(a=2\).
For a vigorous proof, we show that for every \(\varepsilon > 0\) there exists an index \(n_0\in\mathbb{N}\), such that for every term \(a_n\) with \(n>n_0\) the following relationship holds: \[\left| \frac{2n^2+1}{n^2+1} - 2\right| < \varepsilon.\]
Firstly we estimate the inequality: \[\begin{aligned}\left|\frac{2n^2+1}{n^2+1}-2\right| =&\left|\frac{2n^2+1-2\cdot\left(n^2+1\right)}{n^2+1}\right| \\ =&\left|\frac{2n^2+1-2n^2-2}{n^2+1}\right| \\ =&\left|-\frac{1}{n^2+1}\right| \\ =&\left|\frac{1}{n^2+1}\right| \\ <&\frac{1}{n}.\end{aligned}\]
Now, let \(\varepsilon > 0\) be an arbitrary constant. We then choose the index \(n_0\in\mathbb{N}\), such that \[n_0 > \frac{1}{\varepsilon} \text{, or equivalently, } \frac{1}{n_0} < \varepsilon.\] Finally from the above inequality we have: \[\left|\frac{2n^2+1}{n^2+1}-2\right| < \frac{1}{n} < \frac{1}{n_0} < \varepsilon,\] Thus we have proven the claim and so by definition \(a=2\) is the limit of the sequence.
\(\square\)
Jos jono suppenee, niin sillä voi olla vain yksi raja-arvo.
Lause: Raja-arvon yksikäsitteisyys
Oletetaan, että jono \((a_{n})_{n}\) suppenee kohti raja-arvoa \(a\in\mathbb{R}\) ja kohti raja-arvoa \(b\in\mathbb{R}\).
Silloin \(a=b\).
Assume \(a\ne b\); choose \(\varepsilon\in\mathbb{R}\) with \(\varepsilon:=\frac{1}{3}|a-b|.\) Then in particular \([a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset.\)
Because \((a_{n})_{n}\) converges to \(a\), there is, according to the definition of convergence, a index \(n_{0}\in\mathbb{N}\) with \(|a_{n}-a|< \varepsilon\) for \(n\geq n_{0}.\) Furthermore, because \((a_{n})_{n}\) converges to \(b\) there is also a \(\widetilde{n_{0}}\in\mathbb{N}\) with \(|a_{n}-b|< \varepsilon\) for \(n\geq\widetilde{n_{0}}.\) For
\(n\geq\max\{n_{0},\widetilde{n_{0}}\}\) we have:
\[\begin{aligned}\varepsilon\ = &\ \frac{1}{3}|a-b| \Rightarrow\\
3\varepsilon\ = &\ |a-b|\\
= &\ |(a-a_{n})+(a_{n}-b)|\\
\leq &\ |a_{n}-a|+|a_{b}-b|\\
< &\ \varepsilon+\varepsilon=2\varepsilon,\end{aligned}\] Consequently we have obtained \(3\varepsilon\leq2\varepsilon\), which is a contradiction as \(\varepsilon>0\).
Therefore the assumption must be wrong, so \(a=b\).
\(\square\)
Määritelmä: Raja-arvo
Suppenevan jonon raja-arvolle käytetään merkintöjä\[a_{n}\rightarrow a,\text{ tai }\lim_{n\rightarrow\infty}a_{n}=a.\] Määritelmä on yksikäsitteinen yllä
olevan lauseen perusteella. Jos jonolla ei ole raja-arvoa, niin se hajaantuu.
Lause: Rajoitettu jono
Suppeneva jono \((a_n)_n\) on rajoitettu, t.s. on olemassa sellainen vakio \(C\in\mathbb{R}\) että
\[|a_n| \lt C\] kaikilla
\(n\in\mathbb{N}\).
We assume that the sequence \((a_n)_n\) has the limit \(a\). By the definition of convergence, we have that \(|a_n - a|<\varepsilon\) for all \(\varepsilon \in \mathbb{R}\) and \(n\geq n_0\). Choosing \(\varepsilon = 1\) gives:
\[\begin{aligned}|a_n|-|a|&\ \leq |a_n -a| \\
&\ < 1,\end{aligned}\] And therefore also \(|a_n|\leq |a|+1\).
Thus for all \(n\in \mathbb{N}\): \[|a_n|\leq \max \left\{ |a_1|,|a_2|,\ldots,|a_{n_0}|,|a|+1 \right\}=:r\]
\(\square\)
Suppenevien jonojen ominaisuuksia
Lause: Osajono
Olkoon \((a_{n})_{n}\) suppeneva jono, jolle \(a_{n}\rightarrow a\) ja olkoon \((a_{\varphi(n)})_{n}\) jonon \((a_{n})_{n}\) osajono. Silloin \((a_{\varphi(n)})_{n}\rightarrow a\).
Sanallisesti: Suppenevan jonon kaikki osajonot suppenevat kohti alkuperäisen jonon raja-arvoa.
By the definition of a subsequence \(\varphi(n)\geq n\). Because \(a_{n}\rightarrow a\) it is implicated that \(|a_{n}-a|<\varepsilon\) for \(n\geq n_{0}\), therefore \(|a_{\varphi(n)}-a|<\varepsilon\) for these indices \(n\).
\(\square\)
Lause: Laskusääntöjä
Olkoot \((a_{n})_{n}\) ja \((b_{n})_{n}\) suppenevia jonoja, joille \(a_{n}\rightarrow a\) ja \(b_{n}\rightarrow b\). Silloin kaikille \(\lambda, \mu \in \mathbb{R}\) pätee:
-
\(\lambda \cdot (a_n)+\mu \cdot (b_n) \to \lambda \cdot a + \mu \cdot b\)
-
\((a_n)\cdot (b_n) \to a\cdot b\)
Sanallisesti: Suppenevien jonojen summat ja tulot ovat suppenevia jonoja.
Part 1. Let \(\varepsilon > 0\). We must show, that for all \(n \geq n_0\) it follows that: \[|\lambda \cdot a_n + \mu \cdot b_n - \lambda \cdot a - \mu \cdot b| < \varepsilon.\] The left hand side we estimate using: \[|\lambda (a_n-a)+\mu (b_n - b)| \leq |\lambda|\cdot|a_n-a|+|\mu|\cdot|b_n-b|.\]
Because \((a_n)_n\) and \((b_n)_n\) converge, for each given \(\varepsilon > 0\) it holds true that: \[\begin{aligned}|a_n - a| <\ \varepsilon_1 := &\ \textstyle \frac{\varepsilon}{2|\lambda|} \text{ for all }n\geq n_0\\ |b_n - b| <\ \varepsilon_2 := &\ \textstyle \frac{\varepsilon}{2|\mu|} \text{ for all }n\geq n_1\end{aligned}\]
Therefore \[\begin{aligned}|\lambda|\cdot|a_n-a|+|\mu|\cdot|b_n-b| < &\ |\lambda|\varepsilon_1 + |\mu|\varepsilon_2 \\ = &\ \textstyle{ \frac{\varepsilon}{2} + \frac{\varepsilon}{2} } = \varepsilon\end{aligned}\] for all numbers \(n \geq \max \{n_0,n_1\}\). Therefore the sequence \[\left( \lambda \left( a_n - a \right) + \mu \left( b_n - b \right) \right)_n\] is a zero sequence and the desired inequality is shown.
Part 2. Let \(\varepsilon > 0\). We have to show, that for all \(n > n_0\) \[|a_n b_n - a b| < \varepsilon.\] Furthermore an estimation of the left hand side follows: \[\begin{aligned} |a_n b_n - a b| =&\ |a_n b_n - a b_n + a b_n - ab| \\ \leq &\ |b_n|\cdot|a_n-a| + |a|\cdot|b_n - b|.\end{aligned}\] We choose a number \(B\), such that \(|b_n| \lt b\) for all \(n\) and \(|a| \lt b\). Such a value of \(B\) exists by the Theorem of convergent sequences being bounded. We can then use the estimation: \[\begin{aligned}|b_n|\cdot|a_n-a| + |a|\cdot|b_n - b| <&\ B \cdot \left(|a_n - a| + |b_n - b| \right).\end{aligned}\] For all \(n>n_0\) we have \(|a_n - a|<\frac{\varepsilon}{2\cdot B}\) and \(|b_n - b|<\frac{\varepsilon}{2\cdot B}\), and - putting everything together - the desired inequality it shown.
\(\square\)
